人教版8年级下册数学第十九章 一次函数 学案(含答案)
文档属性
| 名称 | 人教版8年级下册数学第十九章 一次函数 学案(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 96.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 16:43:03 | ||
图片预览


文档简介
一次函数
班级:_____________姓名:__________________组号:_________
一次函数
一、知识梳理
(一)一次函数的定义,图象、性质:
1.函数中自变量x的取值范围是___________。
2.若要使函数 的图象过原点,应取_______,若要使其图象和轴交于点,应取_____________。
3.函数y=(k-1)x,y随x增大而减小,则k的范围是_________。
4.若一次函数y=(2-m)x+m的图象经过第一、二、四象限,则m的取值范围是__________。
(二)一次函数与方程、不等式的联系:
5.已知一次函数y=-2x-6。
(1)当x=-4时,则y=_________,当y=-2时,则x=_________;
(2)画出函数图象;
(3)不等式-2x-6>0解集是________,不等式-2x-6<0解集是________;
(4)函数图象与坐标轴围成的三角形的面积为_________;
(5)若直线y=3x+4和直线y=-2x-6交于点A,则点A的坐标____________;
(6)如果y 的取值范围-4≤y≤2,则x的取值范围_____________;
(7)如果x的取值范围-3≤x≤3,则y的最大值是__________,最小值是__________。
二、综合运用
1.已知一次函数的图象经过点(0,1),且图象与x轴、y轴所围成的三角形的面积为2,求一次函数的解析式。
2.如图,直线y=x+b(b>0)与x轴负半轴、y轴正半轴分别交于A、B两点,正比例函数y=kx(k<0)的图象与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=10,BN=7。
(1)求A、B两点的坐标;(用b表示)
(2)图中有全等的三角形吗?若有,请找出并说明理由;
(3)求MN的长。
三、课堂检测
A组:
已知直线y=3x-2, 当x=1时,y= 。
已知直线经过点A(2,3),B(-1,-3),则直线解析式为________________。
点(-1,2)在直线y=2x+4上吗? (填在或不在)
直线y=2x-1与x轴的交点坐标为 与y轴的交点坐标 。
B组:
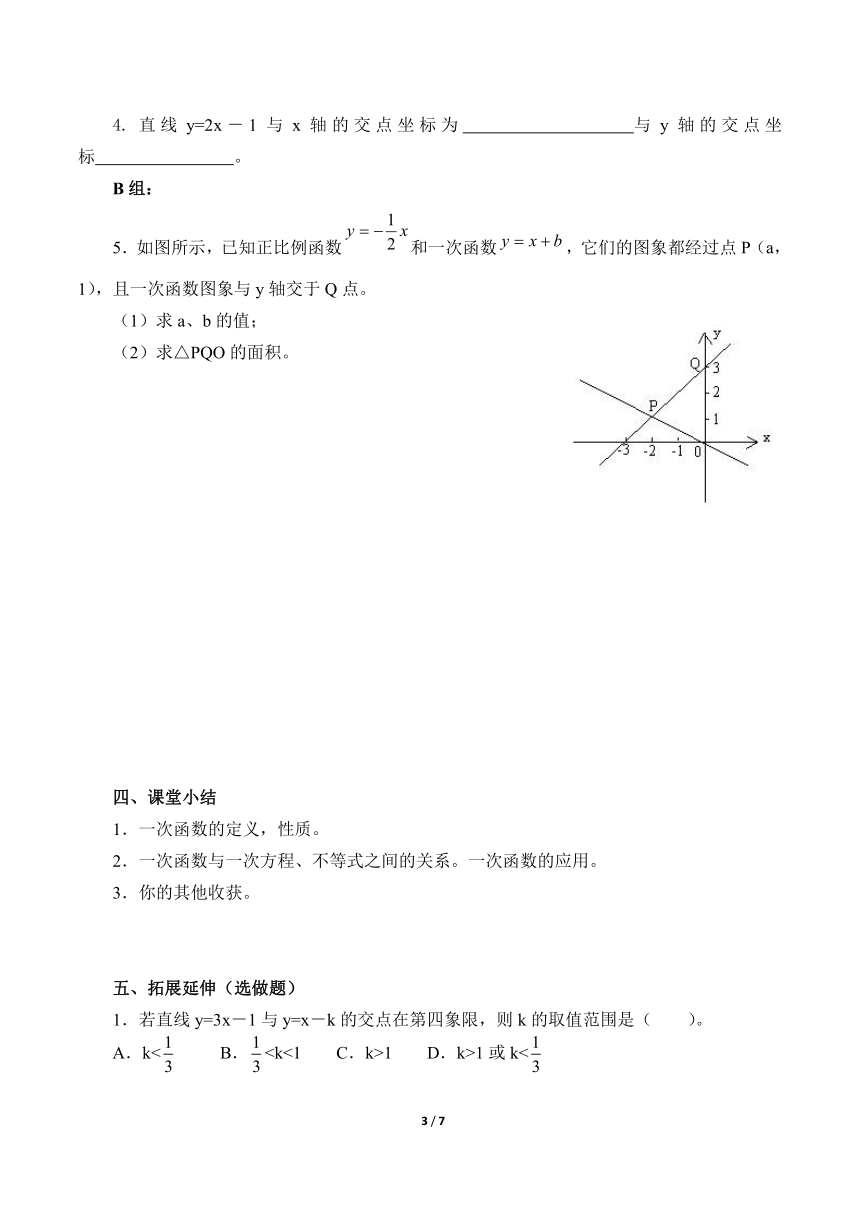
5.如图所示,已知正比例函数和一次函数,它们的图象都经过点P(a,1),且一次函数图象与y轴交于Q点。
(1)求a、b的值;
(2)求△PQO的面积。
四、课堂小结
1.一次函数的定义,性质。
2.一次函数与一次方程、不等式之间的关系。一次函数的应用。
3.你的其他收获。
五、拓展延伸(选做题)
1.若直线y=3x-1与y=x-k的交点在第四象限,则k的取值范围是( )。
A.k< B.1 D.k>1或k<
2.在平面直角坐标系中,点,的坐标分别为,,直线和线段交于点,轴,垂足为点,轴,垂足为点,记,当时,求的取值范围。
【答案】
【知识梳理】
1.
2.;
3.k<1
4.m>2
5.(1)2;-2
(2)略
(3)x<-3;x>-3
(4)9
(5)(-2,-2)
(6)
(7)0;-12
【综合运用】
1解:∵一次函数的图象经过点(0,1)
∴h=1
∴即
∴
∴
2.解:(1)直线y=x+b(b>0)与x轴的交点坐标A为(-b,0),与y轴的交点坐标B为(0,b),
(2)有,△MAO≌△NOB
理由:由(1)知OA=OB
∵AM⊥OQ,BN⊥OQ,
∴∠AMO=∠BNO=90°,
∵∠MOA+∠MAO=90°,∠MOA+∠MOB=90°,
∴∠MAO=∠MOB,
在△MAO和△BON中
∴△MAO≌△NOB,
(3)∵△MAO≌△NOB
∴OM=BN,AM=ON,∵AM=10,BN=3,
∴MN=ON-OM=AM-BN=7.
【课堂检测】
1.1
2.
3.在
4.;
5.解:(1)函数过点P(a,1)∴∴P(-2,1)
把P(-2,1)代入∴b=3
(2)一次函数为
∴解之得 令得
∴S△PQO==
【课堂小结】
略
【拓展延伸】(选做题)
1.B
2.解:把A,B,代入y=kx+b得这个函数的解析式是
直线 和直线相交于D得:解之得
∴=
∵
∴解之得:
7 / 7
班级:_____________姓名:__________________组号:_________
一次函数
一、知识梳理
(一)一次函数的定义,图象、性质:
1.函数中自变量x的取值范围是___________。
2.若要使函数 的图象过原点,应取_______,若要使其图象和轴交于点,应取_____________。
3.函数y=(k-1)x,y随x增大而减小,则k的范围是_________。
4.若一次函数y=(2-m)x+m的图象经过第一、二、四象限,则m的取值范围是__________。
(二)一次函数与方程、不等式的联系:
5.已知一次函数y=-2x-6。
(1)当x=-4时,则y=_________,当y=-2时,则x=_________;
(2)画出函数图象;
(3)不等式-2x-6>0解集是________,不等式-2x-6<0解集是________;
(4)函数图象与坐标轴围成的三角形的面积为_________;
(5)若直线y=3x+4和直线y=-2x-6交于点A,则点A的坐标____________;
(6)如果y 的取值范围-4≤y≤2,则x的取值范围_____________;
(7)如果x的取值范围-3≤x≤3,则y的最大值是__________,最小值是__________。
二、综合运用
1.已知一次函数的图象经过点(0,1),且图象与x轴、y轴所围成的三角形的面积为2,求一次函数的解析式。
2.如图,直线y=x+b(b>0)与x轴负半轴、y轴正半轴分别交于A、B两点,正比例函数y=kx(k<0)的图象与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=10,BN=7。
(1)求A、B两点的坐标;(用b表示)
(2)图中有全等的三角形吗?若有,请找出并说明理由;
(3)求MN的长。
三、课堂检测
A组:
已知直线y=3x-2, 当x=1时,y= 。
已知直线经过点A(2,3),B(-1,-3),则直线解析式为________________。
点(-1,2)在直线y=2x+4上吗? (填在或不在)
直线y=2x-1与x轴的交点坐标为 与y轴的交点坐标 。
B组:
5.如图所示,已知正比例函数和一次函数,它们的图象都经过点P(a,1),且一次函数图象与y轴交于Q点。
(1)求a、b的值;
(2)求△PQO的面积。
四、课堂小结
1.一次函数的定义,性质。
2.一次函数与一次方程、不等式之间的关系。一次函数的应用。
3.你的其他收获。
五、拓展延伸(选做题)
1.若直线y=3x-1与y=x-k的交点在第四象限,则k的取值范围是( )。
A.k< B.
2.在平面直角坐标系中,点,的坐标分别为,,直线和线段交于点,轴,垂足为点,轴,垂足为点,记,当时,求的取值范围。
【答案】
【知识梳理】
1.
2.;
3.k<1
4.m>2
5.(1)2;-2
(2)略
(3)x<-3;x>-3
(4)9
(5)(-2,-2)
(6)
(7)0;-12
【综合运用】
1解:∵一次函数的图象经过点(0,1)
∴h=1
∴即
∴
∴
2.解:(1)直线y=x+b(b>0)与x轴的交点坐标A为(-b,0),与y轴的交点坐标B为(0,b),
(2)有,△MAO≌△NOB
理由:由(1)知OA=OB
∵AM⊥OQ,BN⊥OQ,
∴∠AMO=∠BNO=90°,
∵∠MOA+∠MAO=90°,∠MOA+∠MOB=90°,
∴∠MAO=∠MOB,
在△MAO和△BON中
∴△MAO≌△NOB,
(3)∵△MAO≌△NOB
∴OM=BN,AM=ON,∵AM=10,BN=3,
∴MN=ON-OM=AM-BN=7.
【课堂检测】
1.1
2.
3.在
4.;
5.解:(1)函数过点P(a,1)∴∴P(-2,1)
把P(-2,1)代入∴b=3
(2)一次函数为
∴解之得 令得
∴S△PQO==
【课堂小结】
略
【拓展延伸】(选做题)
1.B
2.解:把A,B,代入y=kx+b得这个函数的解析式是
直线 和直线相交于D得:解之得
∴=
∵
∴解之得:
7 / 7
