人教版八年级下册数学20.2 数据的波动程度 课时练(含答案)
文档属性
| 名称 | 人教版八年级下册数学20.2 数据的波动程度 课时练(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 155.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 17:11:11 | ||
图片预览




文档简介
人教版八年级下册数学
《20.2 数据的波动程度》课时练
1.某班篮球爱好小组10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计,制成如表:
投中次数 2 3 5 6 7 8
人数 1 2 3 2 1 1
则关于这10名队员投中次数组成的数据,下列说法错误的是( )
A.平均数为5 B.中位数为5 C.众数为5 D.方差为5
2.有15名学生参加学校举办的“最强大脑”智力竞赛,比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差,若去掉一个最高分,一个最低分,则一定不会发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
3.某校七年级学生的平均年龄为13岁,年龄的方差为3,若学生人数没有变动,则两年后的同一批学生,对其年龄的说法正确的是( )
A.平均年龄为13岁,方差改变 B.平均年龄为15岁,方差不变
C.平均年龄为15岁,方差改变 D.平均年龄为13岁,方差不变
4.数据2021,2021,2021,2021,2021,2021,2021,2021的方差是( )
A.2021 B.0 C.﹣2021 D.2020
5.下列说法正确的个数是( )
①一组数据的众数只有一个;②样本的方差越小,波动性越小,说明样本稳定性越好;③一组数据的中位数一定是这组数据中的某一数据;④一组数据的众数一定比平均数大;⑤一组数据的方差一定是正数.
A.0个 B.1个 C.2个 D.4个
6.已知一组数据为7,2,5,x,8,它们的平均数是5,则这组数据的方差为( )
A.3 B.4.5 C.5.2 D.6
7.在样本方差的计算式s2=[(x1﹣10)2+(x2﹣10)2+…+(x5﹣10)2]中,数字5和10分别表示样本的( )
A.容量,方差 B.平均数,众数
C.标准差,平均数 D.容量,平均数
8.如图是甲、乙两人6次投篮测试(每次投篮10个)成绩的统计图,甲、乙两人测试成绩方差分别记作S甲2、S乙2,则下列结论正确的是( )
A.S甲2<S乙2 B.S甲2>S乙2 C.S甲2=S乙2 D.无法确定
9.甲、乙、丙、丁四人各进行10次射击测试,它们的平均成绩相同,方差分别是S甲2=1,S乙2=1.1,S丙2=0.6,S丁2=0.9,则射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
10.已知一组数据a1,a2,a3,a4,a5的方差是S1,另一组数据a1﹣6,a2﹣6,a3﹣6,a4﹣6,a5﹣6的方差是S2,则S1与S2的大小关系是S1 S2(填写“>”“<”或“=”).
11.需要对一批排球的质量是否符合标准进行检测,其中质量超过标准的克数记为正数,不足标准的克数记为负数,现抽取8个排球,通过检测所得数据如下(单位:克):+1,﹣2,+1,0,+2,﹣3,0,+1,则这组数据的方差是 .
12.如果一组数据5、8、a、7、4的平均数是a,那么这组数据的方差为 .
13.甲、乙两人5次射击命中的环数如下:
甲 7 9 8 6 10
乙 7 8 9 8 8
则这两人射击成绩波动较大的是 .(填“甲”或“乙”)
14.已知一组数据的方差S2=[(6﹣10)2+(9﹣10)2+(a﹣10)2+(11﹣10)2+(b﹣10)2]=6.8,则a2+b2的值为 .
15.如果样本方差S2=,那么这个样本的平均数是 ,样本容量是 .
16.若一组数据x1+1,x2+1,…,xn+1的平均数为10,方差为1,则另一组数据3x1+2,3x2+2,…,3xn+2的方差是 .
17.一组数据1,0,2,a的唯一众数为1,则这组数据的方差是 .
18.小明用s2=[(x1﹣6)2+(x2﹣6)2+…+(x10﹣6)2]计算一组数据的方差,那么x1+x2+x3+…+x10= .
19.若一组数据x1,x2,…,xn的平均数为5,方差为9,则数据2x1+3,2x2+3,…,2xn+3的平均数为 ,方差为 .
20.如果一组数据1,2,3,4,5的方差是2,那么一组新数据2,4,6,8,10的方差是 .
21.为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书册数分别是:5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是 .
22.某地农业科技部门积极助力家乡农产品的改良与推广,为了解甲、乙两种新品橙子的质量,进行了抽样调查在相同条件下,随机抽取了甲、乙各25份样品,对大小甜度等各方面进行了综合测评,并对数据进行收集、整理、描述和分析,下面给出了部分信息.
a.测评分数(百分制)如下:
甲:77,79,80,80,85,86,86,87,88,89,89,90,91,91,91,91,91,92,93,95,95,96,97,98,98
乙:69,79,79,79,86,87,87,89,89,90,90,90,90,90,91,92,92,92,94,95,96,96,97,98,98
b.按如下分组整理、描述这两组样本数据:
测评分数x个数品种 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
甲 0 2 9 14
乙 1 3 5 16
c.甲、乙两种橙子测评分数的平均数、众数、中位数如下表所示:
品种 平均数 众数 中位数
甲 89.4 m 91
乙 89.4 90 n
根据以上信息,回答下列问题
(1)写出表中m,n的值
(2)记甲种橙子测评分数的方差为s12,乙种橙子测评分数的方差为s22,则s12,s22的大小关系为 ;
(3)根据抽样调查情况,可以推断 种橙子的质量较好,理由为 .(至少从两个不同的角度说明推断的合理性)
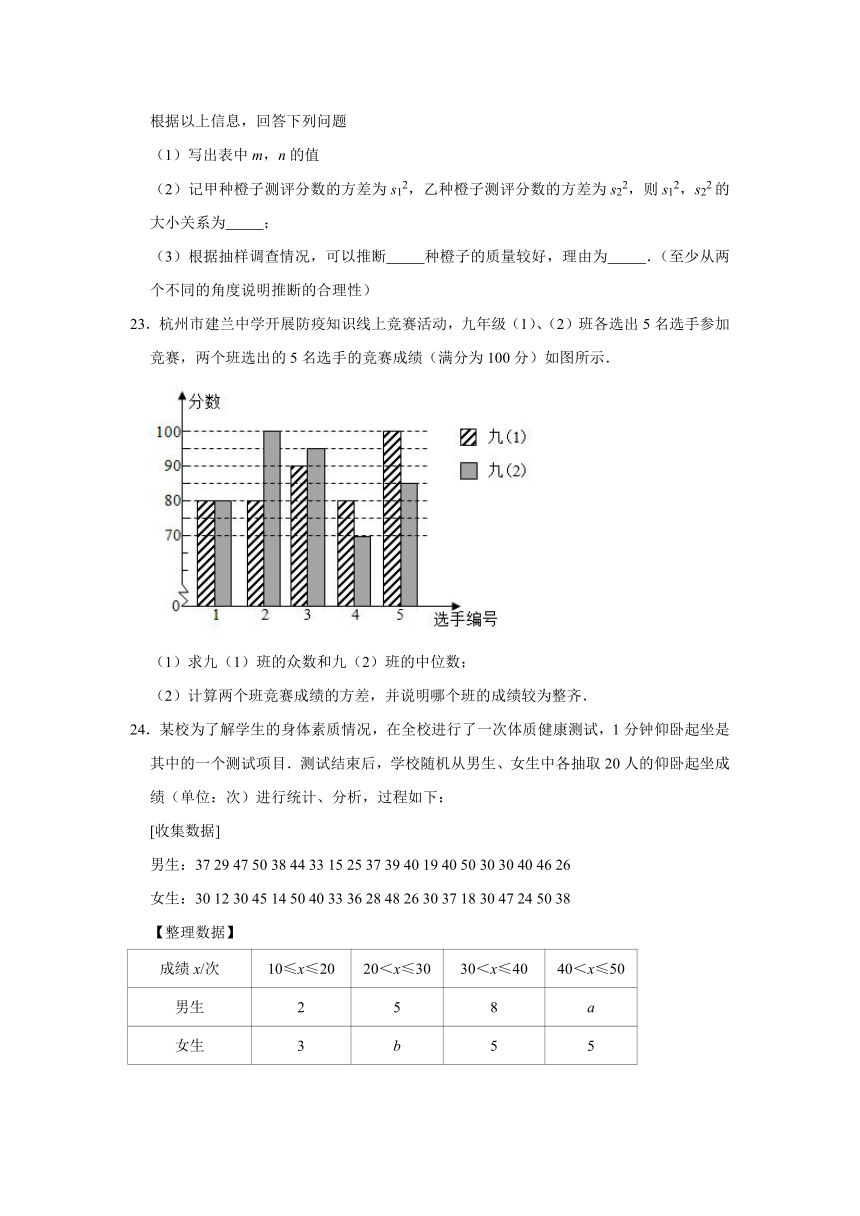
23.杭州市建兰中学开展防疫知识线上竞赛活动,九年级(1)、(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩(满分为100分)如图所示.
(1)求九(1)班的众数和九(2)班的中位数;
(2)计算两个班竞赛成绩的方差,并说明哪个班的成绩较为整齐.
24.某校为了解学生的身体素质情况,在全校进行了一次体质健康测试,1分钟仰卧起坐是其中的一个测试项目.测试结束后,学校随机从男生、女生中各抽取20人的仰卧起坐成绩(单位:次)进行统计、分析,过程如下:
[收集数据]
男生:37 29 47 50 38 44 33 15 25 37 39 40 19 40 50 30 30 40 46 26
女生:30 12 30 45 14 50 40 33 36 28 48 26 30 37 18 30 47 24 50 38
【整理数据】
成绩x/次 10≤x≤20 20<x≤30 30<x≤40 40<x≤50
男生 2 5 8 a
女生 3 b 5 5
【分析数据】
统计量 平均数 中位数 众数 方差
男生 35.75 c 40 90.99(精确到0.01)
女生 33.3 31.5 d 122.91
【应用数据】
(1)填空:a= ,b= ,c= ,d= ;
(2)若男生共有240人参加测试,请估计男生测试成绩大于40次的人数;
(3)有人认为,男生成绩比女生成绩更好些(不考虑男女差异),你认为理由是什么.
25.某市举行知识大赛,A校、B校各派出5名选手组成代表队参加比赛.两校派出选手的比赛成绩如图所示.
根据以上信息.整理分析数据:
平均数/分 中位数/分 众数/分
A校 85 85 85
B校 85 a b
(1)a= ;b= ;
(2)填空:(填“A校”或“B校”)
①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是 ;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是 ;
③从两校比赛成绩的方差的角度来比较, 代表队选手成绩的方差较大.
26.《生物多样性公约》第十五次缔约方大会(COP15)重新确定于2021年5月17日至30日在云南省昆明市举办.“生物多样性”的目标、方法和全球通力合作,将成为国际范围的热点关注内容.为广泛宣传云南生物多样性,某校组织七、八年级各200名学生对《云南的生物多样性》白皮书相关知识进行学习并组织定时测试.现分别在七、八两个年级中各随机抽取了10名学生,统计这部分学生的竞赛成绩,相关数据统计、整理如下:
【收集数据】七年级10名同学测试成绩统计如下:
72,84,72,91,79,69,78,85,75,95
八年级10名同学测试成绩统计如下:
85,72,92,84,80,74,75,80,76,82
【整理数据】两组数据各分数段,如下表所示:
成绩 60≤x<70 70≤x<80 80≤x<90 90≤x<100
七年级 1 5 2 a
八年级 0 4 5 1
【分析数据】两组数据的平均数、中位数、众数、方差如下表:
统计量年级 平均数 中位数 众数 方差
七年级 80 b 72
八年级 80 80 c 33
【问题解决】根据以上信息,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)计算八年级同学测试成绩的方差是:
=×[(80﹣85)2+(80﹣72)2+(80﹣92)2+(80﹣84)2+(80﹣80)2+(80﹣74)2+(80﹣75)2+(80﹣80)2+(80﹣76)2+(80﹣82)2]=33.
请你求出七年级同学成绩的方差,试估计哪个年级的竞赛成绩更整齐?
(3)按照比赛规定90分及其以上算优秀,请估计这两个年级竞赛成绩达到优秀学生的人数共有多少人?
(4)根据以上数据,你认为该校七、八年级中哪个年级学生知识竞赛成绩更好?请说明理由(写出一条理由即可).
27.某商店1~6周销售甲、乙两种品牌冰箱的数量如表(表Ⅰ)所示(单位:台):
第1周 第2周 第3周 第4周 第5周 第6周
甲 9 10 10 9 12 10
乙 13 12 7 11 10 7
现根据表Ⅰ数据进行统计得到表Ⅱ:
平均数 中位数 众数
甲 10
乙 10 7
(1)填空:根据表Ⅰ的数据补全表Ⅱ;
(2)老师计算了乙品牌冰箱销量的方差:
S乙2=[(13﹣10)2+(12﹣10)2+(7﹣10)2+(11﹣10)2+(10﹣10)2+(7﹣10)2]=(台2).
请你计算甲品牌冰箱销量的方差,根据计算结果,建议商家可多采购哪一种品牌冰箱?为什么?
28.某区举办中学生科普知识竞赛,各学校分别派出一支代表队参赛.知识竞赛满分为100分,规定85分及以上为“合格”,95分及以上为“优秀”.现将A,B两个代表队的竞赛成绩分布图及统计表展示如下:
组别 平均分 中位数 方差 合格率 优秀率
A队 88 90 61 70% 30%
B队 a b 71 75% 25%
(1)求出成绩统计表中a,b的值.
(2)小明的成绩虽然在本队排名属中游,但是竞赛成绩低于本队的平均分,那么小明应属于哪个队?
(3)从平均分、合格率、优秀率、队内成绩的整齐性等方面进行综合评价,你认为集体奖应该颁给哪一队?
参考答案
1.D
2.B
3.B
4.B
5.B
6.C
7.D
8.A
9.C
10.=
11.2.5
12.2
13.甲
14.296
15.18;20.
16.9.
17..
18.60.
19.13,36.
20.8
21.5,5,.
22.解:(1)甲品种橙子测评成绩出现次数最多的是91分,所以众数是91,即m=91,
将乙品种橙子的测评成绩从小到大排列处在中间位置的一个数是90,因此中位数是90,即n=90,
答:m=91,n﹣90;
(2)由甲、乙两种橙子的测评成绩的大小波动情况,直观可得s12<s22,
故答案为:<;
(3)甲品种较好,理由为:甲品种橙子的中位数、众数均比乙品种的高.
故答案为:甲,甲品种橙子的中位数、众数均比乙品种的高.
23.解:(1)由图知,九(1)班成绩为80、80、80、90、100,
九(2)班成绩为70、80、85、95、100,
所以九(1)班成绩的众数为80分,九(2)班成绩的中位数为85分;
(2)九(1)班成绩的平均数为=86(分),九(2)班成绩的平均数为=86(分),
∴九(1)班成绩的方差为×[3×(80﹣86)2+(90﹣86)2+(100﹣86)2]=64,
九(2)班成绩的方差为×[(70﹣86)2+(80﹣86)2+(85﹣86)2+(95﹣86)2+(100﹣86)2]=114,
∴九(1)班成绩较为整齐.
24.解:(1)男生:15、19、25、26、29、30、30、33、37、37、38、39、40、40、40、44、46、47、50、50,
女生:12、14、18、24、26、28、30、30、30、30、33、36、37、38、40、45、47、48、50、50,
∴a=5,b=7,男生成绩的中位数c==37.5,女生成绩的众数d=30,
故答案为:5、7、37.5、30;
(2)估计男生测试成绩大于40次的人数为240×=60(人);
(3)男生的平均成绩大于女生,而且男生成绩的中位数大于女生、方差小于女生,即男生高分人数多且成绩稳定.
25.解:(1)将B校5名选手的成绩重新排列为:70、75、80、100、100,
所以其中位数a=80、众数b=100,
故答案为:80、100;
(2)①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是A校;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是B校;
③=×[(75﹣85)2+(80﹣85)2+2×(85﹣85)2+(100﹣85)2]=70,
=×[(70﹣85)2+(75﹣85)2+(80﹣85)2+2×(100﹣85)2]=160,
∴从两校比赛成绩的方差的角度来比较,B校代表队选手成绩的方差较大.
故答案为:A校、B校、B校.
26.解:(1)将七年级抽样成绩重新排列为:69,72,72,75,78,79,84,85,91,95,其中在90≤x<100范围内的数据有2个,
故a=2.
中位数(分),
将八年级样成绩重新排列为:72,74,75,76,80,80,82,84,85,92,
其众数c=80(分),
故答案为:2,78.5,80;
(2)七年级的方差是
,
因为,
所以估计八年级学生的竞赛成绩更整齐些.
(3)(人),
根据样本估计总体的思想,这两个年级竞赛成绩达到优秀学生的人数共约60人.
(4)可以推断出八年级学生的数学水平较高,
理由为两班平均数相同,而八年级的中位数以及众数均高于七年级,
说明八年级学生的竞赛成绩更好(答案不唯一).
27.解:(1)甲品牌销售数量从小到大排列为:9、9、10、10、10、12,
所以甲品牌销售数量的平均数为=10(台),众数为10台,
乙品牌销售数量从小到大排列为7、7、10、11、12、13,
所以乙品牌销售数量的中位数为=10.5(台),
补全表格如下:
平均数 中位数 众数
甲 10 10 10
乙 10 10.5 7
故答案为:10、10、10.5;
(2)建议商家可多采购甲品牌冰箱,
∵甲品牌冰箱销量的方差=×[(9﹣10)2×2+(10﹣10)2×3+(12﹣10)2]=1,S乙2=,
∴<S乙2,
∴甲品牌冰箱的销售量比较稳定,建议商家可多采购甲品牌冰箱.
28.解:(1)B队成绩的平均分a==87(分),中位数b==85(分).
(2)∵A队的中位数为90分高于平均分88分,B队的中位数85分低于平均数87分,
∴小明应该属于B队;
(3)应该颁给A队,理由如下:
①A组的平均数和中位数高于B队,优秀率也高于B队,说明A队的总体平均水平高于B队;
②A队的中位数高于B队,说明A队高分段学生较多;
③虽然B队合格率高于A队,但A队方差低于B队,即A队的成绩比B队的成绩整齐,
所以集体奖应该颁给A队.
《20.2 数据的波动程度》课时练
1.某班篮球爱好小组10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计,制成如表:
投中次数 2 3 5 6 7 8
人数 1 2 3 2 1 1
则关于这10名队员投中次数组成的数据,下列说法错误的是( )
A.平均数为5 B.中位数为5 C.众数为5 D.方差为5
2.有15名学生参加学校举办的“最强大脑”智力竞赛,比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差,若去掉一个最高分,一个最低分,则一定不会发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
3.某校七年级学生的平均年龄为13岁,年龄的方差为3,若学生人数没有变动,则两年后的同一批学生,对其年龄的说法正确的是( )
A.平均年龄为13岁,方差改变 B.平均年龄为15岁,方差不变
C.平均年龄为15岁,方差改变 D.平均年龄为13岁,方差不变
4.数据2021,2021,2021,2021,2021,2021,2021,2021的方差是( )
A.2021 B.0 C.﹣2021 D.2020
5.下列说法正确的个数是( )
①一组数据的众数只有一个;②样本的方差越小,波动性越小,说明样本稳定性越好;③一组数据的中位数一定是这组数据中的某一数据;④一组数据的众数一定比平均数大;⑤一组数据的方差一定是正数.
A.0个 B.1个 C.2个 D.4个
6.已知一组数据为7,2,5,x,8,它们的平均数是5,则这组数据的方差为( )
A.3 B.4.5 C.5.2 D.6
7.在样本方差的计算式s2=[(x1﹣10)2+(x2﹣10)2+…+(x5﹣10)2]中,数字5和10分别表示样本的( )
A.容量,方差 B.平均数,众数
C.标准差,平均数 D.容量,平均数
8.如图是甲、乙两人6次投篮测试(每次投篮10个)成绩的统计图,甲、乙两人测试成绩方差分别记作S甲2、S乙2,则下列结论正确的是( )
A.S甲2<S乙2 B.S甲2>S乙2 C.S甲2=S乙2 D.无法确定
9.甲、乙、丙、丁四人各进行10次射击测试,它们的平均成绩相同,方差分别是S甲2=1,S乙2=1.1,S丙2=0.6,S丁2=0.9,则射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
10.已知一组数据a1,a2,a3,a4,a5的方差是S1,另一组数据a1﹣6,a2﹣6,a3﹣6,a4﹣6,a5﹣6的方差是S2,则S1与S2的大小关系是S1 S2(填写“>”“<”或“=”).
11.需要对一批排球的质量是否符合标准进行检测,其中质量超过标准的克数记为正数,不足标准的克数记为负数,现抽取8个排球,通过检测所得数据如下(单位:克):+1,﹣2,+1,0,+2,﹣3,0,+1,则这组数据的方差是 .
12.如果一组数据5、8、a、7、4的平均数是a,那么这组数据的方差为 .
13.甲、乙两人5次射击命中的环数如下:
甲 7 9 8 6 10
乙 7 8 9 8 8
则这两人射击成绩波动较大的是 .(填“甲”或“乙”)
14.已知一组数据的方差S2=[(6﹣10)2+(9﹣10)2+(a﹣10)2+(11﹣10)2+(b﹣10)2]=6.8,则a2+b2的值为 .
15.如果样本方差S2=,那么这个样本的平均数是 ,样本容量是 .
16.若一组数据x1+1,x2+1,…,xn+1的平均数为10,方差为1,则另一组数据3x1+2,3x2+2,…,3xn+2的方差是 .
17.一组数据1,0,2,a的唯一众数为1,则这组数据的方差是 .
18.小明用s2=[(x1﹣6)2+(x2﹣6)2+…+(x10﹣6)2]计算一组数据的方差,那么x1+x2+x3+…+x10= .
19.若一组数据x1,x2,…,xn的平均数为5,方差为9,则数据2x1+3,2x2+3,…,2xn+3的平均数为 ,方差为 .
20.如果一组数据1,2,3,4,5的方差是2,那么一组新数据2,4,6,8,10的方差是 .
21.为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书册数分别是:5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是 .
22.某地农业科技部门积极助力家乡农产品的改良与推广,为了解甲、乙两种新品橙子的质量,进行了抽样调查在相同条件下,随机抽取了甲、乙各25份样品,对大小甜度等各方面进行了综合测评,并对数据进行收集、整理、描述和分析,下面给出了部分信息.
a.测评分数(百分制)如下:
甲:77,79,80,80,85,86,86,87,88,89,89,90,91,91,91,91,91,92,93,95,95,96,97,98,98
乙:69,79,79,79,86,87,87,89,89,90,90,90,90,90,91,92,92,92,94,95,96,96,97,98,98
b.按如下分组整理、描述这两组样本数据:
测评分数x个数品种 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
甲 0 2 9 14
乙 1 3 5 16
c.甲、乙两种橙子测评分数的平均数、众数、中位数如下表所示:
品种 平均数 众数 中位数
甲 89.4 m 91
乙 89.4 90 n
根据以上信息,回答下列问题
(1)写出表中m,n的值
(2)记甲种橙子测评分数的方差为s12,乙种橙子测评分数的方差为s22,则s12,s22的大小关系为 ;
(3)根据抽样调查情况,可以推断 种橙子的质量较好,理由为 .(至少从两个不同的角度说明推断的合理性)
23.杭州市建兰中学开展防疫知识线上竞赛活动,九年级(1)、(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩(满分为100分)如图所示.
(1)求九(1)班的众数和九(2)班的中位数;
(2)计算两个班竞赛成绩的方差,并说明哪个班的成绩较为整齐.
24.某校为了解学生的身体素质情况,在全校进行了一次体质健康测试,1分钟仰卧起坐是其中的一个测试项目.测试结束后,学校随机从男生、女生中各抽取20人的仰卧起坐成绩(单位:次)进行统计、分析,过程如下:
[收集数据]
男生:37 29 47 50 38 44 33 15 25 37 39 40 19 40 50 30 30 40 46 26
女生:30 12 30 45 14 50 40 33 36 28 48 26 30 37 18 30 47 24 50 38
【整理数据】
成绩x/次 10≤x≤20 20<x≤30 30<x≤40 40<x≤50
男生 2 5 8 a
女生 3 b 5 5
【分析数据】
统计量 平均数 中位数 众数 方差
男生 35.75 c 40 90.99(精确到0.01)
女生 33.3 31.5 d 122.91
【应用数据】
(1)填空:a= ,b= ,c= ,d= ;
(2)若男生共有240人参加测试,请估计男生测试成绩大于40次的人数;
(3)有人认为,男生成绩比女生成绩更好些(不考虑男女差异),你认为理由是什么.
25.某市举行知识大赛,A校、B校各派出5名选手组成代表队参加比赛.两校派出选手的比赛成绩如图所示.
根据以上信息.整理分析数据:
平均数/分 中位数/分 众数/分
A校 85 85 85
B校 85 a b
(1)a= ;b= ;
(2)填空:(填“A校”或“B校”)
①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是 ;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是 ;
③从两校比赛成绩的方差的角度来比较, 代表队选手成绩的方差较大.
26.《生物多样性公约》第十五次缔约方大会(COP15)重新确定于2021年5月17日至30日在云南省昆明市举办.“生物多样性”的目标、方法和全球通力合作,将成为国际范围的热点关注内容.为广泛宣传云南生物多样性,某校组织七、八年级各200名学生对《云南的生物多样性》白皮书相关知识进行学习并组织定时测试.现分别在七、八两个年级中各随机抽取了10名学生,统计这部分学生的竞赛成绩,相关数据统计、整理如下:
【收集数据】七年级10名同学测试成绩统计如下:
72,84,72,91,79,69,78,85,75,95
八年级10名同学测试成绩统计如下:
85,72,92,84,80,74,75,80,76,82
【整理数据】两组数据各分数段,如下表所示:
成绩 60≤x<70 70≤x<80 80≤x<90 90≤x<100
七年级 1 5 2 a
八年级 0 4 5 1
【分析数据】两组数据的平均数、中位数、众数、方差如下表:
统计量年级 平均数 中位数 众数 方差
七年级 80 b 72
八年级 80 80 c 33
【问题解决】根据以上信息,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)计算八年级同学测试成绩的方差是:
=×[(80﹣85)2+(80﹣72)2+(80﹣92)2+(80﹣84)2+(80﹣80)2+(80﹣74)2+(80﹣75)2+(80﹣80)2+(80﹣76)2+(80﹣82)2]=33.
请你求出七年级同学成绩的方差,试估计哪个年级的竞赛成绩更整齐?
(3)按照比赛规定90分及其以上算优秀,请估计这两个年级竞赛成绩达到优秀学生的人数共有多少人?
(4)根据以上数据,你认为该校七、八年级中哪个年级学生知识竞赛成绩更好?请说明理由(写出一条理由即可).
27.某商店1~6周销售甲、乙两种品牌冰箱的数量如表(表Ⅰ)所示(单位:台):
第1周 第2周 第3周 第4周 第5周 第6周
甲 9 10 10 9 12 10
乙 13 12 7 11 10 7
现根据表Ⅰ数据进行统计得到表Ⅱ:
平均数 中位数 众数
甲 10
乙 10 7
(1)填空:根据表Ⅰ的数据补全表Ⅱ;
(2)老师计算了乙品牌冰箱销量的方差:
S乙2=[(13﹣10)2+(12﹣10)2+(7﹣10)2+(11﹣10)2+(10﹣10)2+(7﹣10)2]=(台2).
请你计算甲品牌冰箱销量的方差,根据计算结果,建议商家可多采购哪一种品牌冰箱?为什么?
28.某区举办中学生科普知识竞赛,各学校分别派出一支代表队参赛.知识竞赛满分为100分,规定85分及以上为“合格”,95分及以上为“优秀”.现将A,B两个代表队的竞赛成绩分布图及统计表展示如下:
组别 平均分 中位数 方差 合格率 优秀率
A队 88 90 61 70% 30%
B队 a b 71 75% 25%
(1)求出成绩统计表中a,b的值.
(2)小明的成绩虽然在本队排名属中游,但是竞赛成绩低于本队的平均分,那么小明应属于哪个队?
(3)从平均分、合格率、优秀率、队内成绩的整齐性等方面进行综合评价,你认为集体奖应该颁给哪一队?
参考答案
1.D
2.B
3.B
4.B
5.B
6.C
7.D
8.A
9.C
10.=
11.2.5
12.2
13.甲
14.296
15.18;20.
16.9.
17..
18.60.
19.13,36.
20.8
21.5,5,.
22.解:(1)甲品种橙子测评成绩出现次数最多的是91分,所以众数是91,即m=91,
将乙品种橙子的测评成绩从小到大排列处在中间位置的一个数是90,因此中位数是90,即n=90,
答:m=91,n﹣90;
(2)由甲、乙两种橙子的测评成绩的大小波动情况,直观可得s12<s22,
故答案为:<;
(3)甲品种较好,理由为:甲品种橙子的中位数、众数均比乙品种的高.
故答案为:甲,甲品种橙子的中位数、众数均比乙品种的高.
23.解:(1)由图知,九(1)班成绩为80、80、80、90、100,
九(2)班成绩为70、80、85、95、100,
所以九(1)班成绩的众数为80分,九(2)班成绩的中位数为85分;
(2)九(1)班成绩的平均数为=86(分),九(2)班成绩的平均数为=86(分),
∴九(1)班成绩的方差为×[3×(80﹣86)2+(90﹣86)2+(100﹣86)2]=64,
九(2)班成绩的方差为×[(70﹣86)2+(80﹣86)2+(85﹣86)2+(95﹣86)2+(100﹣86)2]=114,
∴九(1)班成绩较为整齐.
24.解:(1)男生:15、19、25、26、29、30、30、33、37、37、38、39、40、40、40、44、46、47、50、50,
女生:12、14、18、24、26、28、30、30、30、30、33、36、37、38、40、45、47、48、50、50,
∴a=5,b=7,男生成绩的中位数c==37.5,女生成绩的众数d=30,
故答案为:5、7、37.5、30;
(2)估计男生测试成绩大于40次的人数为240×=60(人);
(3)男生的平均成绩大于女生,而且男生成绩的中位数大于女生、方差小于女生,即男生高分人数多且成绩稳定.
25.解:(1)将B校5名选手的成绩重新排列为:70、75、80、100、100,
所以其中位数a=80、众数b=100,
故答案为:80、100;
(2)①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是A校;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是B校;
③=×[(75﹣85)2+(80﹣85)2+2×(85﹣85)2+(100﹣85)2]=70,
=×[(70﹣85)2+(75﹣85)2+(80﹣85)2+2×(100﹣85)2]=160,
∴从两校比赛成绩的方差的角度来比较,B校代表队选手成绩的方差较大.
故答案为:A校、B校、B校.
26.解:(1)将七年级抽样成绩重新排列为:69,72,72,75,78,79,84,85,91,95,其中在90≤x<100范围内的数据有2个,
故a=2.
中位数(分),
将八年级样成绩重新排列为:72,74,75,76,80,80,82,84,85,92,
其众数c=80(分),
故答案为:2,78.5,80;
(2)七年级的方差是
,
因为,
所以估计八年级学生的竞赛成绩更整齐些.
(3)(人),
根据样本估计总体的思想,这两个年级竞赛成绩达到优秀学生的人数共约60人.
(4)可以推断出八年级学生的数学水平较高,
理由为两班平均数相同,而八年级的中位数以及众数均高于七年级,
说明八年级学生的竞赛成绩更好(答案不唯一).
27.解:(1)甲品牌销售数量从小到大排列为:9、9、10、10、10、12,
所以甲品牌销售数量的平均数为=10(台),众数为10台,
乙品牌销售数量从小到大排列为7、7、10、11、12、13,
所以乙品牌销售数量的中位数为=10.5(台),
补全表格如下:
平均数 中位数 众数
甲 10 10 10
乙 10 10.5 7
故答案为:10、10、10.5;
(2)建议商家可多采购甲品牌冰箱,
∵甲品牌冰箱销量的方差=×[(9﹣10)2×2+(10﹣10)2×3+(12﹣10)2]=1,S乙2=,
∴<S乙2,
∴甲品牌冰箱的销售量比较稳定,建议商家可多采购甲品牌冰箱.
28.解:(1)B队成绩的平均分a==87(分),中位数b==85(分).
(2)∵A队的中位数为90分高于平均分88分,B队的中位数85分低于平均数87分,
∴小明应该属于B队;
(3)应该颁给A队,理由如下:
①A组的平均数和中位数高于B队,优秀率也高于B队,说明A队的总体平均水平高于B队;
②A队的中位数高于B队,说明A队高分段学生较多;
③虽然B队合格率高于A队,但A队方差低于B队,即A队的成绩比B队的成绩整齐,
所以集体奖应该颁给A队.
