第五章 平面直角坐标系 单元测试(无答案) 2023—2024学年苏科版数学八年级上册
文档属性
| 名称 | 第五章 平面直角坐标系 单元测试(无答案) 2023—2024学年苏科版数学八年级上册 | 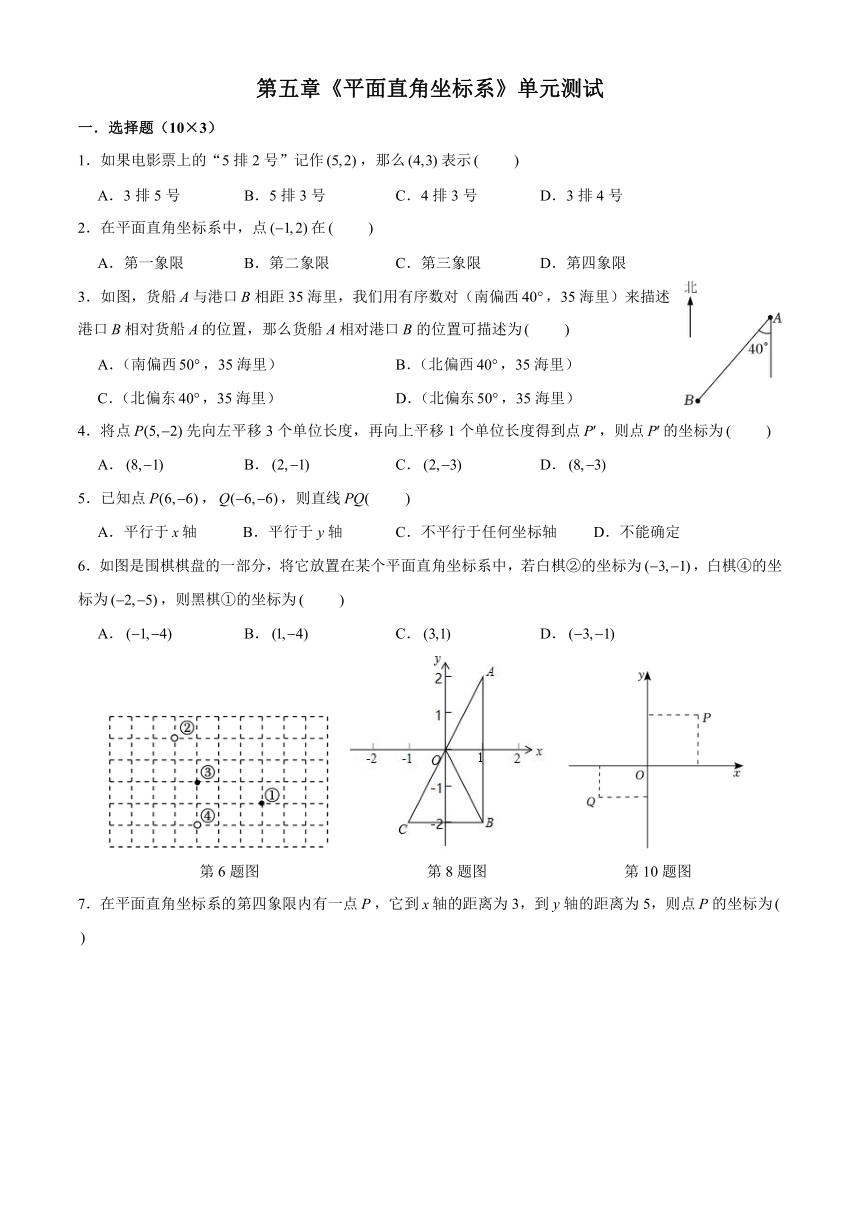 | |
| 格式 | docx | ||
| 文件大小 | 236.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 13:09:18 | ||
图片预览


文档简介
第五章《平面直角坐标系》单元测试
一.选择题(10×3)
1.如果电影票上的“5排2号”记作,那么表示
A.3排5号 B.5排3号 C.4排3号 D.3排4号
2.在平面直角坐标系中,点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,货船与港口相距35海里,我们用有序数对(南偏西,35海里)来描述港口相对货船的位置,那么货船相对港口的位置可描述为
A.(南偏西,35海里) B.(北偏西,35海里)
C.(北偏东,35海里) D.(北偏东,35海里)
4.将点先向左平移3个单位长度,再向上平移1个单位长度得到点,则点的坐标为
A. B. C. D.
5.已知点,,则直线
A.平行于轴 B.平行于轴 C.不平行于任何坐标轴 D.不能确定
6.如图是围棋棋盘的一部分,将它放置在某个平面直角坐标系中,若白棋②的坐标为,白棋④的坐标为,则黑棋①的坐标为
A. B. C. D.
第6题图 第8题图 第10题图
7.在平面直角坐标系的第四象限内有一点,它到轴的距离为3,到轴的距离为5,则点的坐标为
A. B.─3, C. D.
8.如图,轴是的对称轴,轴是的对称轴,点的坐标为,则点的坐标为
A. B. C. D.
9.已知点,在轴上有一点与的距离为5,则该点的坐标为
A. B. C. D.或
10.在平面直角坐标系中,对于,两点给出如下定义:若点到、轴的距离中的最大值等于点到、轴的距离中的最大值,则称,两点为“等距点”.如图中的,两点即为“等距点”.若点的坐标为,点的坐标为,且,两点为“等距点”,则点的坐标为
A. B. C. D.
二.填空题(8×3)
11.在平面直角坐标系中,点A(3,﹣2)到x轴的距离是 ,到y轴的距离是 ,与B(0,﹣2)的距离是 .
12.点与点关于 对称;点与点关于 对称;点与点关于 对称.
13.在平面直角坐标系中,点在第四象限,则的取值范围是 .
14.已知点的坐标是,线段轴,且,则点的坐标是 .
15.在平面直角坐标系中,已知点,若是轴上一动点,则,两点间的距离的最小值为 .
16.如图,将点绕原点顺时针旋转得到点,则点的坐标为 .
第16题图 第17题图 第18题图
17.如图,已知点A(0,2),B,4,0),点P(m,3),若三角形PAO的面积等于三角形ABO
的面积,则点P的坐标为 .
18.如图,在平面直角坐标系中,,,,,点在轴上,满足,则点的坐标为 .
三.解答题(共46分)
19.(6分)已知在平面直角坐标系中,点A的坐标为(a﹣1,2a+1).
(1)若点A在y轴上,求出点A的坐标;
(2)若点A在第一象限,且到x轴的距离为5,求出点A的坐标.
20.(10分)为了更好的开展古树名木的系统保护工作,某公园对园内的6棵百年古树都利用坐标确定了位置,并且定期巡视.
(1)在如图所示的正方形网格中建立平面直角坐标系,使得古树,的位置分别表示为,;
(2)在(1)建立的平面直角坐标系中,
①表示古树的位置的坐标为 ;
②标出古树,,的位置.
21.(8分)已知点是平面直角坐标系中的点.
(1)若点在第二象限的角平分线上,求的值;
(2)若点在第三象限,且到两坐标轴的距离和为9,请确定点的坐标.
22.(10分)如图,平面直角坐标系中,长方形,点,分别在轴、轴的正半轴上,点
(6,3),现将△OAB沿OB翻折至△OA’B位置,OA’交交于点P.
(1)求证:△OCP≌△A’PB;
(2)求点P的坐标.
23.(12分)在平面直角坐标系中,为原点,点,,.
(1)如图(1),三角形的面积为 ;
(
备用图
)
(2)如图(2),将点向右平移7个单位长度,再向上平移4个单位长度,得到对应点.
①求三角形的面积;
②在图(2)中过点C作CE⊥x轴,交线段AD于点E,求线段CE的长度
③若点P在y轴上,且△PCA为等腰三角形,直接写出P的坐标为________.
一.选择题(10×3)
1.如果电影票上的“5排2号”记作,那么表示
A.3排5号 B.5排3号 C.4排3号 D.3排4号
2.在平面直角坐标系中,点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,货船与港口相距35海里,我们用有序数对(南偏西,35海里)来描述港口相对货船的位置,那么货船相对港口的位置可描述为
A.(南偏西,35海里) B.(北偏西,35海里)
C.(北偏东,35海里) D.(北偏东,35海里)
4.将点先向左平移3个单位长度,再向上平移1个单位长度得到点,则点的坐标为
A. B. C. D.
5.已知点,,则直线
A.平行于轴 B.平行于轴 C.不平行于任何坐标轴 D.不能确定
6.如图是围棋棋盘的一部分,将它放置在某个平面直角坐标系中,若白棋②的坐标为,白棋④的坐标为,则黑棋①的坐标为
A. B. C. D.
第6题图 第8题图 第10题图
7.在平面直角坐标系的第四象限内有一点,它到轴的距离为3,到轴的距离为5,则点的坐标为
A. B.─3, C. D.
8.如图,轴是的对称轴,轴是的对称轴,点的坐标为,则点的坐标为
A. B. C. D.
9.已知点,在轴上有一点与的距离为5,则该点的坐标为
A. B. C. D.或
10.在平面直角坐标系中,对于,两点给出如下定义:若点到、轴的距离中的最大值等于点到、轴的距离中的最大值,则称,两点为“等距点”.如图中的,两点即为“等距点”.若点的坐标为,点的坐标为,且,两点为“等距点”,则点的坐标为
A. B. C. D.
二.填空题(8×3)
11.在平面直角坐标系中,点A(3,﹣2)到x轴的距离是 ,到y轴的距离是 ,与B(0,﹣2)的距离是 .
12.点与点关于 对称;点与点关于 对称;点与点关于 对称.
13.在平面直角坐标系中,点在第四象限,则的取值范围是 .
14.已知点的坐标是,线段轴,且,则点的坐标是 .
15.在平面直角坐标系中,已知点,若是轴上一动点,则,两点间的距离的最小值为 .
16.如图,将点绕原点顺时针旋转得到点,则点的坐标为 .
第16题图 第17题图 第18题图
17.如图,已知点A(0,2),B,4,0),点P(m,3),若三角形PAO的面积等于三角形ABO
的面积,则点P的坐标为 .
18.如图,在平面直角坐标系中,,,,,点在轴上,满足,则点的坐标为 .
三.解答题(共46分)
19.(6分)已知在平面直角坐标系中,点A的坐标为(a﹣1,2a+1).
(1)若点A在y轴上,求出点A的坐标;
(2)若点A在第一象限,且到x轴的距离为5,求出点A的坐标.
20.(10分)为了更好的开展古树名木的系统保护工作,某公园对园内的6棵百年古树都利用坐标确定了位置,并且定期巡视.
(1)在如图所示的正方形网格中建立平面直角坐标系,使得古树,的位置分别表示为,;
(2)在(1)建立的平面直角坐标系中,
①表示古树的位置的坐标为 ;
②标出古树,,的位置.
21.(8分)已知点是平面直角坐标系中的点.
(1)若点在第二象限的角平分线上,求的值;
(2)若点在第三象限,且到两坐标轴的距离和为9,请确定点的坐标.
22.(10分)如图,平面直角坐标系中,长方形,点,分别在轴、轴的正半轴上,点
(6,3),现将△OAB沿OB翻折至△OA’B位置,OA’交交于点P.
(1)求证:△OCP≌△A’PB;
(2)求点P的坐标.
23.(12分)在平面直角坐标系中,为原点,点,,.
(1)如图(1),三角形的面积为 ;
(
备用图
)
(2)如图(2),将点向右平移7个单位长度,再向上平移4个单位长度,得到对应点.
①求三角形的面积;
②在图(2)中过点C作CE⊥x轴,交线段AD于点E,求线段CE的长度
③若点P在y轴上,且△PCA为等腰三角形,直接写出P的坐标为________.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
