第一章 丰富的图形世界 期末复习(无答案) 2023—2024学年鲁教版(五四制)数学六年级上册
文档属性
| 名称 | 第一章 丰富的图形世界 期末复习(无答案) 2023—2024学年鲁教版(五四制)数学六年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 512.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 00:00:00 | ||
图片预览




文档简介
第一章 丰富的图形世界
考点一:棱柱的概念及特征
1.下列物体的形状类似于长方体的是 ( )
A.西瓜 B.砖块 C.沙堆 D.蒙古包
2.下列说法中,正确的是 ( )
A.正方体不是棱柱 B.圆锥是由3个面围成
C.正方体的各条棱都相等 D.棱柱的各条棱都相等
3.下列说法错误的是 ( )
A.长方体、正方体都是棱柱
B.三棱柱的侧面是三角形
C.直六棱柱有六个侧面且侧面为长方形
D.棱柱的底面都是多边形
4. 若一个棱柱有30条棱,那么该棱柱有________个面.
5.如图所示的几何体是由一个正方体截去后而形成的,这个几何体是由________个面围成的,其中正方形有________个,长方形有________个.
6. 一个直六棱柱模型,它的上、下底面的形状、大小都相同,底面边长都是5cm,侧棱长为4cm,则它的所有侧面的面积之和为________cm2.
考点二:几何体的分类
1.下面几何体中,全是由曲面围成的是 ( )
A.圆柱 B.圆锥 C.球 D.正方体
2. 下列几何体中,属于棱柱的是 ( )
A.①③ B.① C.①③⑥ D.①⑥
3.若一个棱柱的底面是一个七边形,则它的侧面必须有________个长方形,它一共有________个面.
4. 生活中的立体图形主要有________、________、________,其中柱体包括________和________,锥体包括________和________.
5. 将图中的几何体进行分类,并说明理由.
考点三:几何体的形成
1.笔尖在纸上快速滑动写出一个又一个字,用数学知识解释为 ( )
A.点动成线 B.线动成面
C.面动成体 D.以上答案都不对
2. 一张纸对折形成一条折痕,用数学知识可以解释为 ( )
A.点动成线 B.线动成面
C.面动成体 D.面与面相交得到线
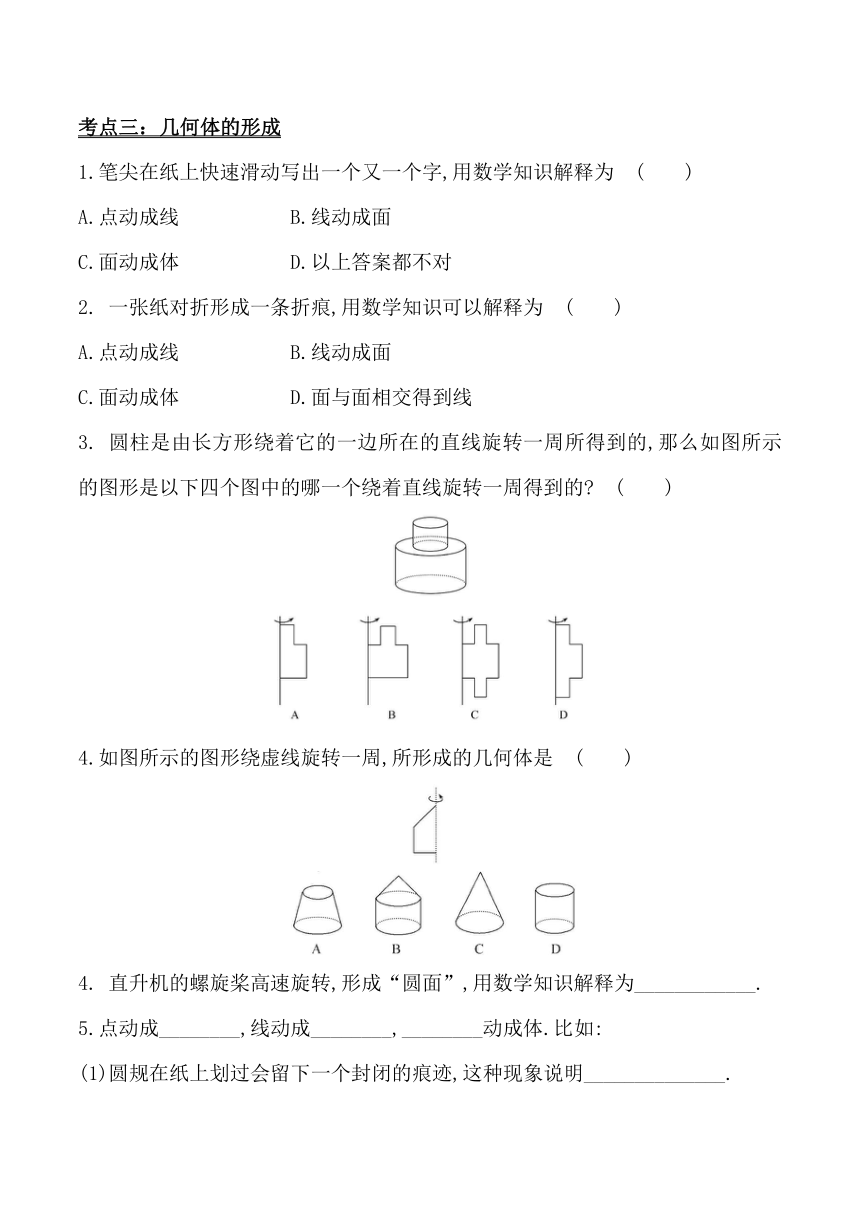
3. 圆柱是由长方形绕着它的一边所在的直线旋转一周所得到的,那么如图所示的图形是以下四个图中的哪一个绕着直线旋转一周得到的 ( )
4.如图所示的图形绕虚线旋转一周,所形成的几何体是 ( )
4. 直升机的螺旋桨高速旋转,形成“圆面”,用数学知识解释为____________.
5.点动成________,线动成________,________动成体.比如:
(1)圆规在纸上划过会留下一个封闭的痕迹,这种现象说明______________.
(2)一个人手里拿着一个绑在一根棍上的半圆面,当这个人把这个半圆面绕着这根棍飞快地旋转起来时,就会看到一个球,这种现象说明______________.
(3)冬天环卫工人使用下部是长方形的木锨推雪时,木锨过处,雪就没了,这种现象说明______________.
7.直角三角形的两直角边长分别为4cm,3cm,以其中一条直角边所在直线为轴旋转一周,得到的几何体的底面积是________.
考点四:几何体的展开与折叠
1.在下列立体图形中,侧面展开图是矩形的是 ( )
2. 图中各硬纸片,不可以沿虚线折叠成长方体纸盒的是 ( )
A.①② B.②③ C.③④ D.①④
3.下列图形中可以作为一个三棱柱的展开图的是 ( )
4. 下列图形中,能通过折叠围成一个三棱柱的是 ( )
5.一个长为40、宽为20的矩形纸片,以它的一边作为底面的周长,围成一个底面是正方形的正四棱柱的侧面,则这个棱柱的体积是________.
6. 如图所示的图形可以被折成一个长方体,则该长方体的表面积为 cm2.
7. 如图是一个棱柱形状的食品包装盒的侧面展开图.
(1)请写出这个包装盒的多面体形状的名称 .(2)根据图中所标的尺寸,计算这个多面体的侧面积.
考点五:正方体的展开与折叠
1. 下图中是正方体的展开图的共有________个. ( )
A.2 B.3 C.4 D.5
2. 图(1)是一个小正方体的表面展开图,小正方体从图(2)所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是 ( )
A.梦 B.水 C.城 D.美
3. 下列四个图形中是正方体的平面展开图的是 ( )
4.如图,是一个正方体纸盒展开图,按直线折成正方体后,若使相对面上的两数互为相反数,则A,B,C表示的数依次是 .
5. 如图,立方体的六个面上标着连续的整数,若相对的两个面上所标之数的和相等,则这六个数的和为______.
6. 如图是正方体的一种表面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“香”相对的面上的汉字是 .
7. 将如图所示的正方体的展开图重新折叠成正方体后,和“应”字相对的面上的汉字是 .
8.如图所示,若剪去一个正方形,使剩余的部分恰好能折成一个正方体,问应剪去哪个小正方形
9.一个正方体的表面展开图如图所示,已知这个正方体的每一个面上都填有一个数字,且各相对面上所填的数字互为倒数,请写出x,y,z的值.
考点六:截一个几何体
1. 一个几何体的一个截面是三角形,则原几何体一定不是下列图形中的 ( )
A.圆柱和圆锥 B.球体和圆锥 C.球体和圆柱 D.正方体和圆锥
2. 如图所示,几何体截面的形状是 ( )
3. 从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积是 ( )
A.20 B.22 C.24 D.26
4. 如图所示,过长方体的一个顶点,截掉长方体的一个角,则剩余部分的顶点有__ __个.
5.用一个平面截正方体,若所得的截面是一个三角形,则留下的较大的一块几何体一定有__ __个面.
6. 一个四棱柱被一刀切去一部分,剩下的部分可能是__ __.
7. 用一个平面去截一个圆柱:
(1)所得截面可能是三角形吗
(2)如果能得到正方形的截面,那么圆柱的底面半径和高有什么关系
8. 如图②是圆柱被一个平面斜切后得到的几何体,请类比梯形面积公式的推导方法(如图①),推导图②几何体的体积为多少?(结果保留π)
9. 如图1至图3是将正方体截去一部分后得到的多面体.
(1)根据要求填写表格:
面数(f) 顶点数(v) 棱数(e)
图1 ________ ________ ________
图2 ________ ________ ________
图3 ________ ________ ________
(2)猜想f,v,e三个数量间有何关系.
(3)根据猜想计算,若一个多面体有顶点数2021个,棱数4041条,试求出它的面数.
考点七:从三个方向看物体的形状图
1. 下列物体从正面看到的图形是圆的是 ( )
2. 下列几何体从正面看与其他三个不同的是 ( )
3. 从不同方向看一只茶壶,你认为从上面看到的图形是 ( )
4. 某几何体从三个方向看到的图形如图所示,这个几何体是( )
A.圆锥 B.圆柱 C.三棱柱 D.三棱锥
5. 任意放置以下几何体:正方体、圆柱、圆锥、球体,则从三个方向看到的图形都完全相同的几何体是________.
考点八:由从三个方向看到的图形判断原几何体
1. 由一些大小相同的小正方体搭成的几何体,从正面和上面看到的图形如图所示,则搭成该几何体的方式有 ( )
A.1种 B.2种 C.3种 D.4种
2. 如图,甲、乙、丙三个图形都是由大小相同的小正方体搭成的几何体从上面看到的图形,小正方形中的数字表示该位置小正方体的个数.其中从正面看到的图形相同的是 ( )
A.仅有甲和乙相同 B.仅有甲和丙相同
C.仅有乙和丙相同 D.甲、乙、丙都相同
3. 如图是由几个相同的小正方体搭成的几何体从三个方向看到的形状图,则搭成这个几何体的小正方体的个数是 ( )
A.4个 B.5个 C.6个 D.7个
4. 一个几何体,是由许多规格相同的小正方体堆积而成的,其从正面看、从左面看到的形状图如图所示,要摆成这样的图形,最少需用________个正方体.
5.一个几何体从三个方向看到的是两个同样大小的长方形和一个直径等于长方形一边长的圆,这个几何体是________.
6.如图是从上面看到的一些小正方体所搭几何体的形状图,小正方形中的数字表示该位置的小正方体的个数,请画出这个几何体从正面和左面看到的形状图.
考点九:根据从三个方向看到的图形的有关计算
1. 由若干个边长为1cm的正方体堆积成的一个几何体,从三个方向看到的图形如图所示,则这个几何体的表面积是 ( )
A.15 cm2 B.18 cm2 C.21 cm2 D.24 cm2
2. 一个几何体从三个方向看到的图形如图,则该几何体的侧面展开图的面积
为 ( )
A.8cm2 B.4πcm2 C.8πcm2 D.10πcm2
3. 已知圆柱按如图所示方式放置,从左面看到的图形的面积为48,则该圆柱的侧面积为________.
4. 长方体从正面和上面看到的图形如图所示,则其从左面看到的图形的面积为________.
5. 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体从上面和左面看到的图形的面积之和是________.
6. 如图是一个长方体从三个方向看到的图形(单位:cm),根据图中数据计算这个长方体的体积是________cm3.
7.如图是由7个完全相同的小正方体搭成的几何体,已知每个小正方体的棱长为2cm.
(1)画出该几何体从三个方向看到的图形.
(2)求出该几何体的表面积.
考点一:棱柱的概念及特征
1.下列物体的形状类似于长方体的是 ( )
A.西瓜 B.砖块 C.沙堆 D.蒙古包
2.下列说法中,正确的是 ( )
A.正方体不是棱柱 B.圆锥是由3个面围成
C.正方体的各条棱都相等 D.棱柱的各条棱都相等
3.下列说法错误的是 ( )
A.长方体、正方体都是棱柱
B.三棱柱的侧面是三角形
C.直六棱柱有六个侧面且侧面为长方形
D.棱柱的底面都是多边形
4. 若一个棱柱有30条棱,那么该棱柱有________个面.
5.如图所示的几何体是由一个正方体截去后而形成的,这个几何体是由________个面围成的,其中正方形有________个,长方形有________个.
6. 一个直六棱柱模型,它的上、下底面的形状、大小都相同,底面边长都是5cm,侧棱长为4cm,则它的所有侧面的面积之和为________cm2.
考点二:几何体的分类
1.下面几何体中,全是由曲面围成的是 ( )
A.圆柱 B.圆锥 C.球 D.正方体
2. 下列几何体中,属于棱柱的是 ( )
A.①③ B.① C.①③⑥ D.①⑥
3.若一个棱柱的底面是一个七边形,则它的侧面必须有________个长方形,它一共有________个面.
4. 生活中的立体图形主要有________、________、________,其中柱体包括________和________,锥体包括________和________.
5. 将图中的几何体进行分类,并说明理由.
考点三:几何体的形成
1.笔尖在纸上快速滑动写出一个又一个字,用数学知识解释为 ( )
A.点动成线 B.线动成面
C.面动成体 D.以上答案都不对
2. 一张纸对折形成一条折痕,用数学知识可以解释为 ( )
A.点动成线 B.线动成面
C.面动成体 D.面与面相交得到线
3. 圆柱是由长方形绕着它的一边所在的直线旋转一周所得到的,那么如图所示的图形是以下四个图中的哪一个绕着直线旋转一周得到的 ( )
4.如图所示的图形绕虚线旋转一周,所形成的几何体是 ( )
4. 直升机的螺旋桨高速旋转,形成“圆面”,用数学知识解释为____________.
5.点动成________,线动成________,________动成体.比如:
(1)圆规在纸上划过会留下一个封闭的痕迹,这种现象说明______________.
(2)一个人手里拿着一个绑在一根棍上的半圆面,当这个人把这个半圆面绕着这根棍飞快地旋转起来时,就会看到一个球,这种现象说明______________.
(3)冬天环卫工人使用下部是长方形的木锨推雪时,木锨过处,雪就没了,这种现象说明______________.
7.直角三角形的两直角边长分别为4cm,3cm,以其中一条直角边所在直线为轴旋转一周,得到的几何体的底面积是________.
考点四:几何体的展开与折叠
1.在下列立体图形中,侧面展开图是矩形的是 ( )
2. 图中各硬纸片,不可以沿虚线折叠成长方体纸盒的是 ( )
A.①② B.②③ C.③④ D.①④
3.下列图形中可以作为一个三棱柱的展开图的是 ( )
4. 下列图形中,能通过折叠围成一个三棱柱的是 ( )
5.一个长为40、宽为20的矩形纸片,以它的一边作为底面的周长,围成一个底面是正方形的正四棱柱的侧面,则这个棱柱的体积是________.
6. 如图所示的图形可以被折成一个长方体,则该长方体的表面积为 cm2.
7. 如图是一个棱柱形状的食品包装盒的侧面展开图.
(1)请写出这个包装盒的多面体形状的名称 .(2)根据图中所标的尺寸,计算这个多面体的侧面积.
考点五:正方体的展开与折叠
1. 下图中是正方体的展开图的共有________个. ( )
A.2 B.3 C.4 D.5
2. 图(1)是一个小正方体的表面展开图,小正方体从图(2)所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是 ( )
A.梦 B.水 C.城 D.美
3. 下列四个图形中是正方体的平面展开图的是 ( )
4.如图,是一个正方体纸盒展开图,按直线折成正方体后,若使相对面上的两数互为相反数,则A,B,C表示的数依次是 .
5. 如图,立方体的六个面上标着连续的整数,若相对的两个面上所标之数的和相等,则这六个数的和为______.
6. 如图是正方体的一种表面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“香”相对的面上的汉字是 .
7. 将如图所示的正方体的展开图重新折叠成正方体后,和“应”字相对的面上的汉字是 .
8.如图所示,若剪去一个正方形,使剩余的部分恰好能折成一个正方体,问应剪去哪个小正方形
9.一个正方体的表面展开图如图所示,已知这个正方体的每一个面上都填有一个数字,且各相对面上所填的数字互为倒数,请写出x,y,z的值.
考点六:截一个几何体
1. 一个几何体的一个截面是三角形,则原几何体一定不是下列图形中的 ( )
A.圆柱和圆锥 B.球体和圆锥 C.球体和圆柱 D.正方体和圆锥
2. 如图所示,几何体截面的形状是 ( )
3. 从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积是 ( )
A.20 B.22 C.24 D.26
4. 如图所示,过长方体的一个顶点,截掉长方体的一个角,则剩余部分的顶点有__ __个.
5.用一个平面截正方体,若所得的截面是一个三角形,则留下的较大的一块几何体一定有__ __个面.
6. 一个四棱柱被一刀切去一部分,剩下的部分可能是__ __.
7. 用一个平面去截一个圆柱:
(1)所得截面可能是三角形吗
(2)如果能得到正方形的截面,那么圆柱的底面半径和高有什么关系
8. 如图②是圆柱被一个平面斜切后得到的几何体,请类比梯形面积公式的推导方法(如图①),推导图②几何体的体积为多少?(结果保留π)
9. 如图1至图3是将正方体截去一部分后得到的多面体.
(1)根据要求填写表格:
面数(f) 顶点数(v) 棱数(e)
图1 ________ ________ ________
图2 ________ ________ ________
图3 ________ ________ ________
(2)猜想f,v,e三个数量间有何关系.
(3)根据猜想计算,若一个多面体有顶点数2021个,棱数4041条,试求出它的面数.
考点七:从三个方向看物体的形状图
1. 下列物体从正面看到的图形是圆的是 ( )
2. 下列几何体从正面看与其他三个不同的是 ( )
3. 从不同方向看一只茶壶,你认为从上面看到的图形是 ( )
4. 某几何体从三个方向看到的图形如图所示,这个几何体是( )
A.圆锥 B.圆柱 C.三棱柱 D.三棱锥
5. 任意放置以下几何体:正方体、圆柱、圆锥、球体,则从三个方向看到的图形都完全相同的几何体是________.
考点八:由从三个方向看到的图形判断原几何体
1. 由一些大小相同的小正方体搭成的几何体,从正面和上面看到的图形如图所示,则搭成该几何体的方式有 ( )
A.1种 B.2种 C.3种 D.4种
2. 如图,甲、乙、丙三个图形都是由大小相同的小正方体搭成的几何体从上面看到的图形,小正方形中的数字表示该位置小正方体的个数.其中从正面看到的图形相同的是 ( )
A.仅有甲和乙相同 B.仅有甲和丙相同
C.仅有乙和丙相同 D.甲、乙、丙都相同
3. 如图是由几个相同的小正方体搭成的几何体从三个方向看到的形状图,则搭成这个几何体的小正方体的个数是 ( )
A.4个 B.5个 C.6个 D.7个
4. 一个几何体,是由许多规格相同的小正方体堆积而成的,其从正面看、从左面看到的形状图如图所示,要摆成这样的图形,最少需用________个正方体.
5.一个几何体从三个方向看到的是两个同样大小的长方形和一个直径等于长方形一边长的圆,这个几何体是________.
6.如图是从上面看到的一些小正方体所搭几何体的形状图,小正方形中的数字表示该位置的小正方体的个数,请画出这个几何体从正面和左面看到的形状图.
考点九:根据从三个方向看到的图形的有关计算
1. 由若干个边长为1cm的正方体堆积成的一个几何体,从三个方向看到的图形如图所示,则这个几何体的表面积是 ( )
A.15 cm2 B.18 cm2 C.21 cm2 D.24 cm2
2. 一个几何体从三个方向看到的图形如图,则该几何体的侧面展开图的面积
为 ( )
A.8cm2 B.4πcm2 C.8πcm2 D.10πcm2
3. 已知圆柱按如图所示方式放置,从左面看到的图形的面积为48,则该圆柱的侧面积为________.
4. 长方体从正面和上面看到的图形如图所示,则其从左面看到的图形的面积为________.
5. 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体从上面和左面看到的图形的面积之和是________.
6. 如图是一个长方体从三个方向看到的图形(单位:cm),根据图中数据计算这个长方体的体积是________cm3.
7.如图是由7个完全相同的小正方体搭成的几何体,已知每个小正方体的棱长为2cm.
(1)画出该几何体从三个方向看到的图形.
(2)求出该几何体的表面积.
