第24章 圆---隐圆专题讲义(无答案)
文档属性
| 名称 | 第24章 圆---隐圆专题讲义(无答案) | 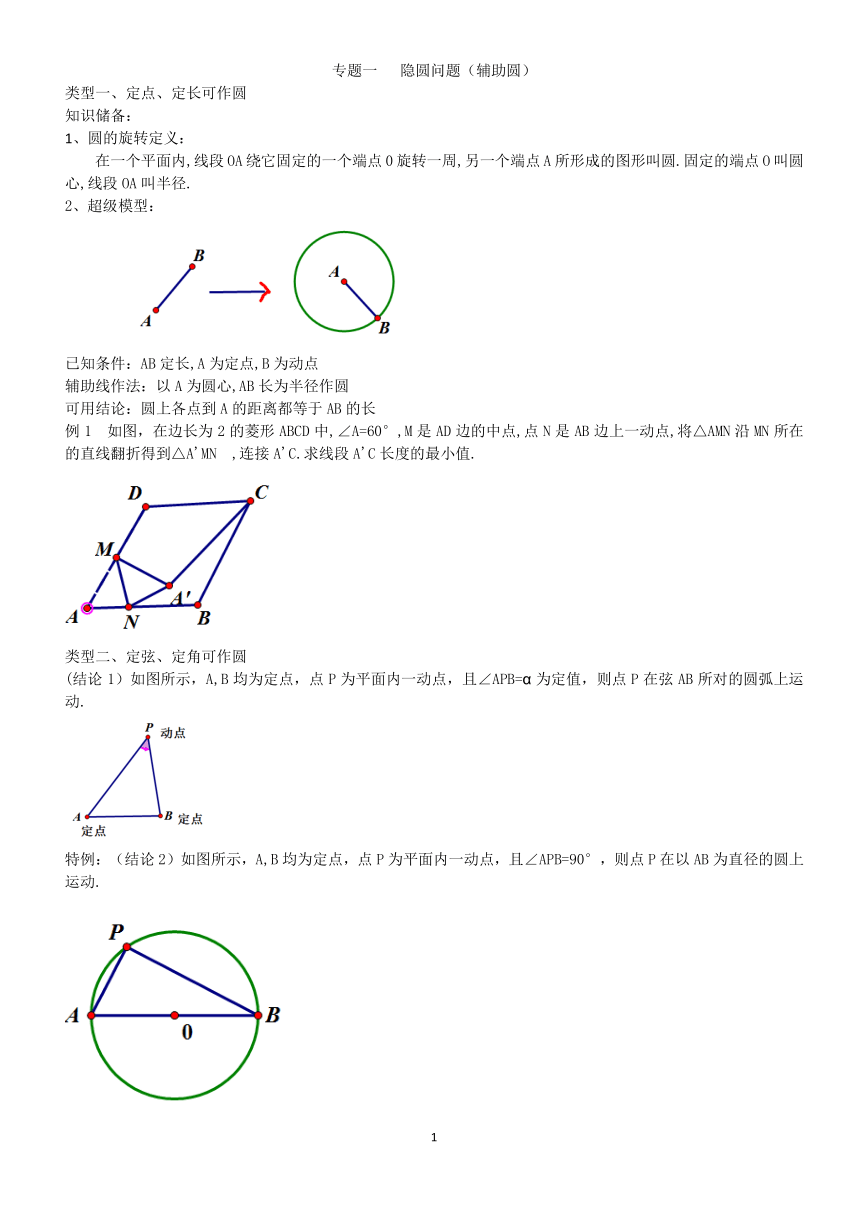 | |
| 格式 | docx | ||
| 文件大小 | 208.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 17:22:20 | ||
图片预览

文档简介
专题一 隐圆问题(辅助圆)
类型一、定点、定长可作圆
知识储备:
1、圆的旋转定义:
在一个平面内,线段OA绕它固定的一个端点0旋转一周,另一个端点A所形成的图形叫圆.固定的端点O叫圆心,线段OA叫半径.
超级模型:
已知条件:AB定长,A为定点,B为动点
辅助线作法:以A为圆心,AB长为半径作圆
可用结论:圆上各点到A的距离都等于AB的长
例1 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A'MN ,连接A'C.求线段A'C长度的最小值.
类型二、定弦、定角可作圆
(结论1)如图所示,A,B均为定点,点P为平面内一动点,且∠APB=α为定值,则点P在弦AB所对的圆弧上运动.
特例:(结论2)如图所示,A,B均为定点,点P为平面内一动点,且∠APB=90°,则点P在以AB为直径的圆上运动.
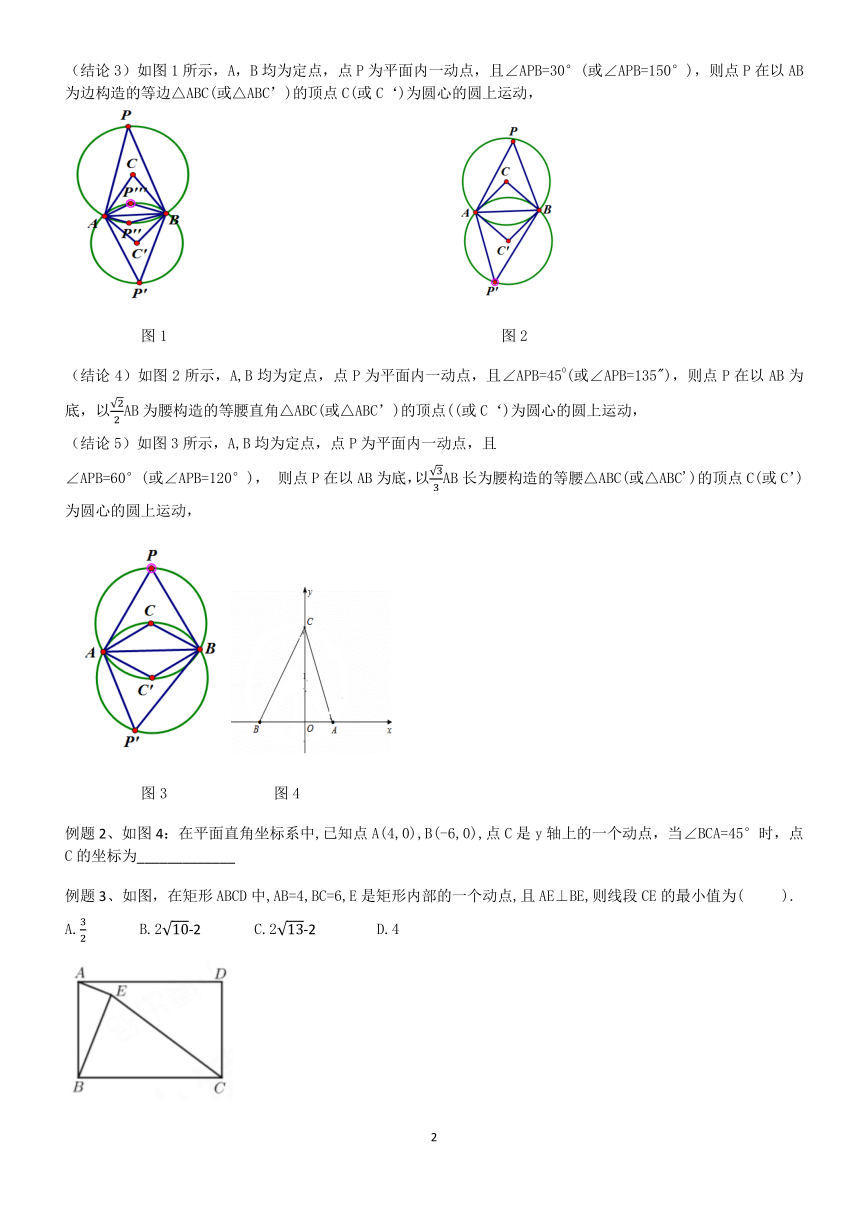
(结论3)如图1所示,A,B均为定点,点P为平面内一动点,且∠APB=30°(或∠APB=150°),则点P在以AB为边构造的等边△ABC(或△ABC’)的顶点C(或C‘)为圆心的圆上运动,
图1 图2
(结论4)如图2所示,A,B均为定点,点P为平面内一动点,且∠APB=450(或∠APB=135"),则点P在以AB为底,以AB为腰构造的等腰直角△ABC(或△ABC’)的顶点((或C‘)为圆心的圆上运动,
(结论5)如图3所示,A,B均为定点,点P为平面内一动点,且
∠APB=60°(或∠APB=120°), 则点P在以AB为底,以AB长为腰构造的等腰△ABC(或△ABC')的顶点C(或C’)为圆心的圆上运动,
图3 图4
例题2、如图4:在平面直角坐标系中,已知点A(4,0),B(-6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为_____________
例题3、如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( ).
A. B.2-2 C.2-2 D.4
例题4、如图,在平面直角坐标系中,A(-3,0),B(3,0),C(3,4),点P为任意一点,已知PA⊥PB,则线段PC的最大值为( ).
A.3 B.5 C.8 D.10
例题5、如图,在Rt△ABC中,AB⊥BC,AB=10,BC=12,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段PC的最小值为( ).
A.7 B.8 C. D.
练习:1、如图所示,已知正方形ABCD的边长为2,E是边BC上的动点.BF⊥AE,交CD于点F,垂足为G,连接CG.下列说法:①AG>GE;②AE=BF;③点G运动的运动轨迹为圆;④CG的最小值为-1.其中,正确的说法是________(把你认为正确的说法的序号都填上)
练习:2、如图,已知半圆O,OB=,点D在半圆.上,AD=10,在取点C,连接AC,作DH⊥AC于点H,连接BH,则BH的最小值等于
练习:3、如图,⊙O的半径是5,点A是圆周上一定点,点B在⊙O上运动,且∠ABM=30°,AC⊥BM,垂足为点C,连接OC,则OC的最小值是 .
类型一、定点、定长可作圆
知识储备:
1、圆的旋转定义:
在一个平面内,线段OA绕它固定的一个端点0旋转一周,另一个端点A所形成的图形叫圆.固定的端点O叫圆心,线段OA叫半径.
超级模型:
已知条件:AB定长,A为定点,B为动点
辅助线作法:以A为圆心,AB长为半径作圆
可用结论:圆上各点到A的距离都等于AB的长
例1 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A'MN ,连接A'C.求线段A'C长度的最小值.
类型二、定弦、定角可作圆
(结论1)如图所示,A,B均为定点,点P为平面内一动点,且∠APB=α为定值,则点P在弦AB所对的圆弧上运动.
特例:(结论2)如图所示,A,B均为定点,点P为平面内一动点,且∠APB=90°,则点P在以AB为直径的圆上运动.
(结论3)如图1所示,A,B均为定点,点P为平面内一动点,且∠APB=30°(或∠APB=150°),则点P在以AB为边构造的等边△ABC(或△ABC’)的顶点C(或C‘)为圆心的圆上运动,
图1 图2
(结论4)如图2所示,A,B均为定点,点P为平面内一动点,且∠APB=450(或∠APB=135"),则点P在以AB为底,以AB为腰构造的等腰直角△ABC(或△ABC’)的顶点((或C‘)为圆心的圆上运动,
(结论5)如图3所示,A,B均为定点,点P为平面内一动点,且
∠APB=60°(或∠APB=120°), 则点P在以AB为底,以AB长为腰构造的等腰△ABC(或△ABC')的顶点C(或C’)为圆心的圆上运动,
图3 图4
例题2、如图4:在平面直角坐标系中,已知点A(4,0),B(-6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为_____________
例题3、如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( ).
A. B.2-2 C.2-2 D.4
例题4、如图,在平面直角坐标系中,A(-3,0),B(3,0),C(3,4),点P为任意一点,已知PA⊥PB,则线段PC的最大值为( ).
A.3 B.5 C.8 D.10
例题5、如图,在Rt△ABC中,AB⊥BC,AB=10,BC=12,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段PC的最小值为( ).
A.7 B.8 C. D.
练习:1、如图所示,已知正方形ABCD的边长为2,E是边BC上的动点.BF⊥AE,交CD于点F,垂足为G,连接CG.下列说法:①AG>GE;②AE=BF;③点G运动的运动轨迹为圆;④CG的最小值为-1.其中,正确的说法是________(把你认为正确的说法的序号都填上)
练习:2、如图,已知半圆O,OB=,点D在半圆.上,AD=10,在取点C,连接AC,作DH⊥AC于点H,连接BH,则BH的最小值等于
练习:3、如图,⊙O的半径是5,点A是圆周上一定点,点B在⊙O上运动,且∠ABM=30°,AC⊥BM,垂足为点C,连接OC,则OC的最小值是 .
同课章节目录
