北京市2023-2024学年高一上学期第二次质量检测数学试卷(PDF版无答案)
文档属性
| 名称 | 北京市2023-2024学年高一上学期第二次质量检测数学试卷(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 222.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-26 21:43:17 | ||
图片预览

文档简介
2023-2024 学年第一学期第二次质量检测
数 学
命题组:高一数学组 考试时间:120 分钟
本试卷分为选择题(共 50 分)和非选择题(共 100 分)两部分
第 I卷(选择题)
一、选择题(本大题共 10 小题,每小题 5 分。共 50 分)
1.已知集合 A x 1 x 1 ,B x 0 x 2 ,则 A B ( )
A. x 0 x 1 B. x 1 x 2 C. x 0 x 1 D. x 1 x 2
2. 命题“ x 1,都有 ln x x 1 0”的否定是( )
A.“ x 1,都有 ln x x 1 0 ” B.“ x0 1,使 ln x0 x0 1 0 ”
C.“ x0 1,使 ln x0 x0 1 0” D.“ x0 1,使 ln x0 x0 1 0 ”
3. 下列函数中,既是偶函数又在 0, 上单调递增的是( )
A. y log2x B. y x 1
1
C. y x2 1 D. y x
1 3.1 14. 已知 a ,b 3.12 ,c lg
1
,则 a,b,c的大小关系为( )
2 2
A. c5. 函数 f x x3 x 7的零点所在的区间是( )
A. 0,1 B. 1,2 C. 2,3 D. 3, 4
6. 已知 f x x2 m 2 x 2在区间 1,3 上是单调函数,则实数m的取值范围是( )
A. ,0 B. 4,
C. ,0 4, D. , 0 U 4,
2x, x 27. 设函数 f x 2 ,若 f a 1 f 2a 1 x , x 2 ,则实数
a的取值范围是( )
A. ( , 1] B. ( , 2] C. 2,6 D.[2, )
试卷第 1页,共 4页
{#{QQABJQwAogAoQBAAABgCQwnQCACQkACAAAoGgBAMMAAAwQFABCA=}#}
8. 若定义在 R 上的奇函数 f x 在 0, 上是增函数,又 f 4 0,则不等式 x f x 0的
解集为( )
A. x x 4或 4 x 0 B. x 0 x 4或x 4
C. x x 4或x 4 D. x 0 x 4或 4 x 0
9. 已知 a,b R ,则“ lna lnb 0 ”是“ a 1 b 1 0 ”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
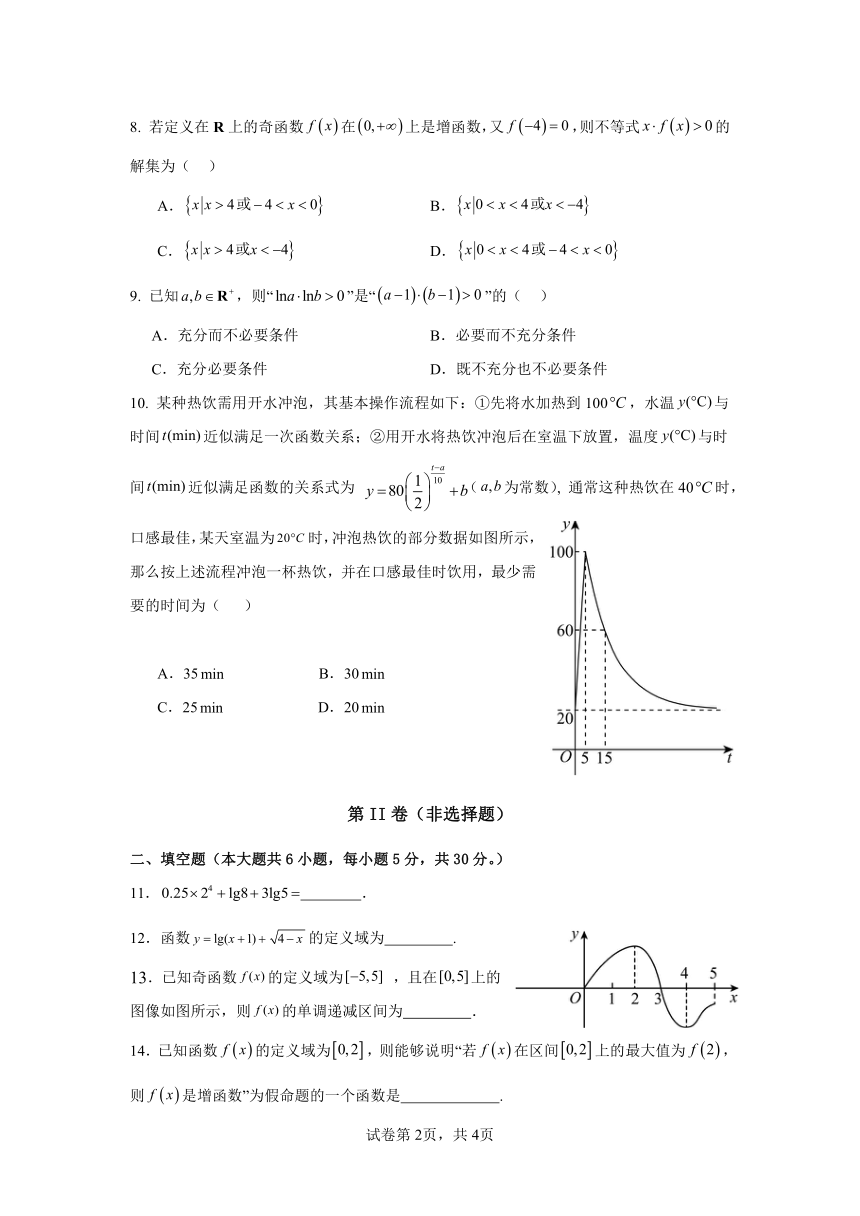
10. 某种热饮需用开水冲泡,其基本操作流程如下:①先将水加热到 100 C,水温 y( C)与
时间 t(min)近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度 y( C)与时
t a
间 t(min) 10近似满足函数的关系式为 y 80 1 b( a,b为常数), 通常这种热饮在 40 C时,
2
口感最佳,某天室温为 20 C 时,冲泡热饮的部分数据如图所示,
那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需
要的时间为( )
A.35min B.30min
C.25min D.20min
第 II 卷(非选择题)
二、填空题(本大题共 6 小题,每小题 5 分,共 30 分。)
11.0.25 24 lg8 3lg5 .
12.函数 y lg(x 1) 4 x 的定义域为 .
13.已知奇函数 f (x)的定义域为[ 5,5] ,且在[0,5]上的
图像如图所示,则 f (x)的单调递减区间为 .
14.已知函数 f x 的定义域为 0,2 ,则能够说明“若 f x 在区间 0,2 上的最大值为 f 2 ,
则 f x 是增函数”为假命题的一个函数是 .
试卷第 2页,共 4页
{#{QQABJQwAogAoQBAAABgCQwnQCACQkACAAAoGgBAMMAAAwQFABCA=}#}
x
15.设全集U R,集合 A y y log x, x 1 2 2 ,集合 B x y , y m ,若 A B U,
2
则实数 m的取值范围是 .
x2 4x 3, x 0
16.设函数 f x 1 .给出下列四个结论:
, x 0 x
①函数 f x 的值域是R ;
f x f x
② x1, x2 ( 2,
) x 1 21 x2 ,有 0;x1 x2
③ x0 0,使得 f x0 f x0 ;
④若互不相等的实数 x1, x2 , x3满足 f x1 f x2 f x3 ,则 x1 x2 x3 的取值范围是
3, .
其中所有正确结论的序号是 .
三、解答题(本大题共 5 小题,共 70 分。解答应写出文字说明,演算步骤或证明过程。)
17. (本小题满分 14 分)
已知集合 A x∣1 2 x 8 ,B x∣x 2 3x 4 0 .
(1) 求集合 A与集合 B;
(2) 求 A B及CR A B ;
(3) 若集合C {x∣a x a 1},且 A C C,求实数 a的取值范围.
18.(本小题满分 14 分)
设函数 f x 是定义在R 上的偶函数,若当 x [0, )时,
f x x2 2x 3,
(1) 求当 x ,0 时,函数 f x 的解析式;
(2) 画出函数图象,并求满足 f x 0的 x的取值范围;
(3) 若方程 f x k 0有四个实数根,求 k的取值范围.
试卷第 3页,共 4页
{#{QQABJQwAogAoQBAAABgCQwnQCACQkACAAAoGgBAMMAAAwQFABCA=}#}
19.(本小题满分 14 分)
x
已知函数 f x 2 .x 1
(1) 判断函数 f x 的奇偶性,并证明;
(2) 判断函数 f x 在 1, 上的单调性,并用定义证明;
(3) 直接写出函数 f x 的值域.(无需写出推理过程)
20.(本小题满分 14 分)
已知二次函数 f (x) x 2 2ax 2.
(1) 若1 x 5时,不等式 f (x) 3ax恒成立,求实数 a的取值范围;
(2) 解关于 x的不等式 (a 1)x2 x f (x)(其中 a R).
21. (本小题满分 14 分)
设函数 f x x2 bx c b,c R ,已知 f (x) 0的解集为 1,3 .
(1)求b,c的值;
(2)若函数 g(x) f (x) ax在区间 0,2 上的最小值为 4,求实数 a的值.
试卷第 4页,共 4页
{#{QQABJQwAogAoQBAAABgCQwnQCACQkACAAAoGgBAMMAAAwQFABCA=}#}
数 学
命题组:高一数学组 考试时间:120 分钟
本试卷分为选择题(共 50 分)和非选择题(共 100 分)两部分
第 I卷(选择题)
一、选择题(本大题共 10 小题,每小题 5 分。共 50 分)
1.已知集合 A x 1 x 1 ,B x 0 x 2 ,则 A B ( )
A. x 0 x 1 B. x 1 x 2 C. x 0 x 1 D. x 1 x 2
2. 命题“ x 1,都有 ln x x 1 0”的否定是( )
A.“ x 1,都有 ln x x 1 0 ” B.“ x0 1,使 ln x0 x0 1 0 ”
C.“ x0 1,使 ln x0 x0 1 0” D.“ x0 1,使 ln x0 x0 1 0 ”
3. 下列函数中,既是偶函数又在 0, 上单调递增的是( )
A. y log2x B. y x 1
1
C. y x2 1 D. y x
1 3.1 14. 已知 a ,b 3.12 ,c lg
1
,则 a,b,c的大小关系为( )
2 2
A. c
A. 0,1 B. 1,2 C. 2,3 D. 3, 4
6. 已知 f x x2 m 2 x 2在区间 1,3 上是单调函数,则实数m的取值范围是( )
A. ,0 B. 4,
C. ,0 4, D. , 0 U 4,
2x, x 27. 设函数 f x 2 ,若 f a 1 f 2a 1 x , x 2 ,则实数
a的取值范围是( )
A. ( , 1] B. ( , 2] C. 2,6 D.[2, )
试卷第 1页,共 4页
{#{QQABJQwAogAoQBAAABgCQwnQCACQkACAAAoGgBAMMAAAwQFABCA=}#}
8. 若定义在 R 上的奇函数 f x 在 0, 上是增函数,又 f 4 0,则不等式 x f x 0的
解集为( )
A. x x 4或 4 x 0 B. x 0 x 4或x 4
C. x x 4或x 4 D. x 0 x 4或 4 x 0
9. 已知 a,b R ,则“ lna lnb 0 ”是“ a 1 b 1 0 ”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
10. 某种热饮需用开水冲泡,其基本操作流程如下:①先将水加热到 100 C,水温 y( C)与
时间 t(min)近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度 y( C)与时
t a
间 t(min) 10近似满足函数的关系式为 y 80 1 b( a,b为常数), 通常这种热饮在 40 C时,
2
口感最佳,某天室温为 20 C 时,冲泡热饮的部分数据如图所示,
那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需
要的时间为( )
A.35min B.30min
C.25min D.20min
第 II 卷(非选择题)
二、填空题(本大题共 6 小题,每小题 5 分,共 30 分。)
11.0.25 24 lg8 3lg5 .
12.函数 y lg(x 1) 4 x 的定义域为 .
13.已知奇函数 f (x)的定义域为[ 5,5] ,且在[0,5]上的
图像如图所示,则 f (x)的单调递减区间为 .
14.已知函数 f x 的定义域为 0,2 ,则能够说明“若 f x 在区间 0,2 上的最大值为 f 2 ,
则 f x 是增函数”为假命题的一个函数是 .
试卷第 2页,共 4页
{#{QQABJQwAogAoQBAAABgCQwnQCACQkACAAAoGgBAMMAAAwQFABCA=}#}
x
15.设全集U R,集合 A y y log x, x 1 2 2 ,集合 B x y , y m ,若 A B U,
2
则实数 m的取值范围是 .
x2 4x 3, x 0
16.设函数 f x 1 .给出下列四个结论:
, x 0 x
①函数 f x 的值域是R ;
f x f x
② x1, x2 ( 2,
) x 1 21 x2 ,有 0;x1 x2
③ x0 0,使得 f x0 f x0 ;
④若互不相等的实数 x1, x2 , x3满足 f x1 f x2 f x3 ,则 x1 x2 x3 的取值范围是
3, .
其中所有正确结论的序号是 .
三、解答题(本大题共 5 小题,共 70 分。解答应写出文字说明,演算步骤或证明过程。)
17. (本小题满分 14 分)
已知集合 A x∣1 2 x 8 ,B x∣x 2 3x 4 0 .
(1) 求集合 A与集合 B;
(2) 求 A B及CR A B ;
(3) 若集合C {x∣a x a 1},且 A C C,求实数 a的取值范围.
18.(本小题满分 14 分)
设函数 f x 是定义在R 上的偶函数,若当 x [0, )时,
f x x2 2x 3,
(1) 求当 x ,0 时,函数 f x 的解析式;
(2) 画出函数图象,并求满足 f x 0的 x的取值范围;
(3) 若方程 f x k 0有四个实数根,求 k的取值范围.
试卷第 3页,共 4页
{#{QQABJQwAogAoQBAAABgCQwnQCACQkACAAAoGgBAMMAAAwQFABCA=}#}
19.(本小题满分 14 分)
x
已知函数 f x 2 .x 1
(1) 判断函数 f x 的奇偶性,并证明;
(2) 判断函数 f x 在 1, 上的单调性,并用定义证明;
(3) 直接写出函数 f x 的值域.(无需写出推理过程)
20.(本小题满分 14 分)
已知二次函数 f (x) x 2 2ax 2.
(1) 若1 x 5时,不等式 f (x) 3ax恒成立,求实数 a的取值范围;
(2) 解关于 x的不等式 (a 1)x2 x f (x)(其中 a R).
21. (本小题满分 14 分)
设函数 f x x2 bx c b,c R ,已知 f (x) 0的解集为 1,3 .
(1)求b,c的值;
(2)若函数 g(x) f (x) ax在区间 0,2 上的最小值为 4,求实数 a的值.
试卷第 4页,共 4页
{#{QQABJQwAogAoQBAAABgCQwnQCACQkACAAAoGgBAMMAAAwQFABCA=}#}
同课章节目录
