4.2.2 等差数列的前n项和 课件(共23张PPT)
文档属性
| 名称 | 4.2.2 等差数列的前n项和 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-26 22:20:34 | ||
图片预览





文档简介
(共23张PPT)
第四章 数列
4.2.2 等差数列的前n项和
一、课题导入
1. 等差数列定义:
2. 等差数列通项公式:
(2) an=am+(n-m)d .
(3) an=pn+q (p、q是常数)
(1) an=a1+(n-1)d (n≥1).
an-an-1 =d (n≥2)
或 an+1-an =d.
3. 几种计算公差d 的方法:
4. 等差中项
m+n=p+q am+an=ap+aq .
5. 等差数列的性质
d=an-an-1 (n≥2)
二、引导探究1——等差数列的前n项和
据说,200多年前,高斯的算术老师提出了下面的问题:1+2+3+---+99+100=
当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面的方法迅速算出了正确答案,那他是怎么算的呢?
问题:计算1+2+ +100=?
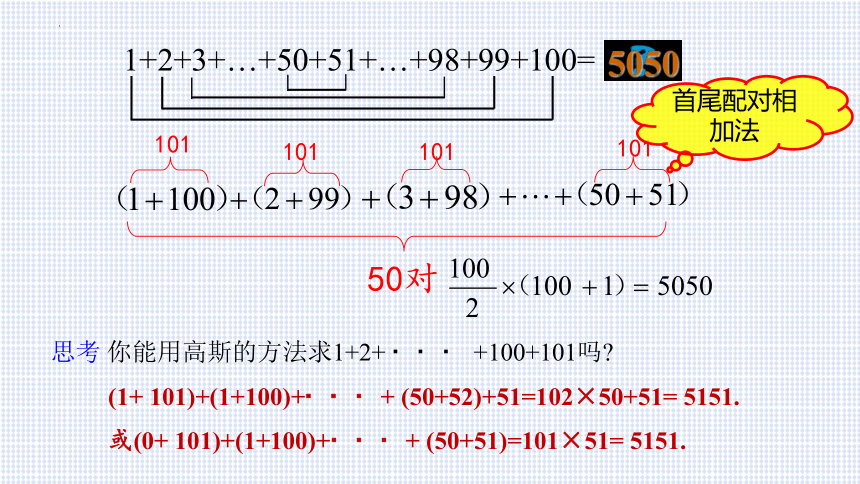
1+2+3+…+50+51+…+98+99+100=
5050
50对
101
101
101
101
思考 你能用高斯的方法求1+2+ +100+101吗
(1+ 101)+(1+100)+ + (50+52)+51=102×50+51= 5151.
或(0+ 101)+(1+100)+ + (50+51)=101×51= 5151.
首尾配对相加法
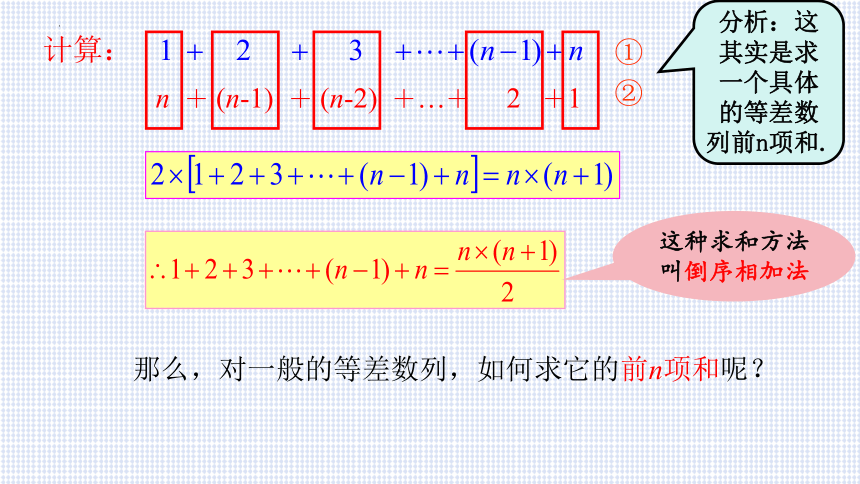
n + (n-1) + (n-2) +…+ 2 +1
那么,对一般的等差数列,如何求它的前n项和呢?
分析:这其实是求一个具体的等差数列前n项和.
①
②
这种求和方法叫倒序相加法
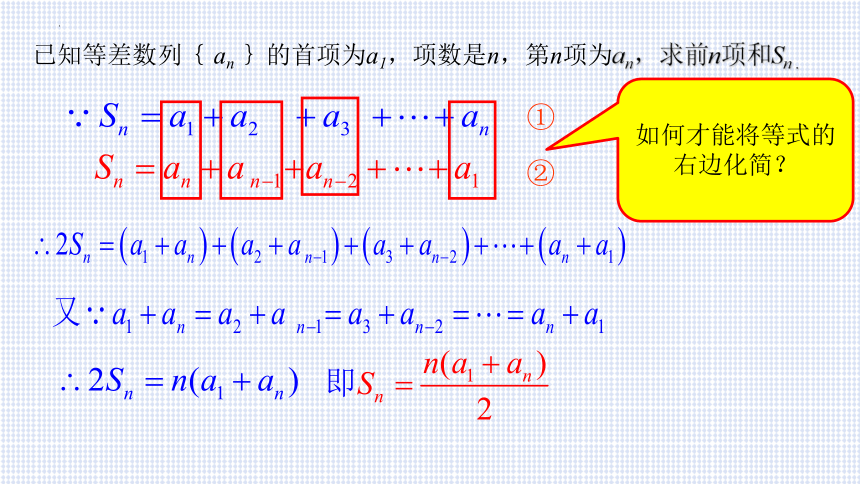
已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .
如何才能将等式的右边化简?
①
②
项数
首项
末项
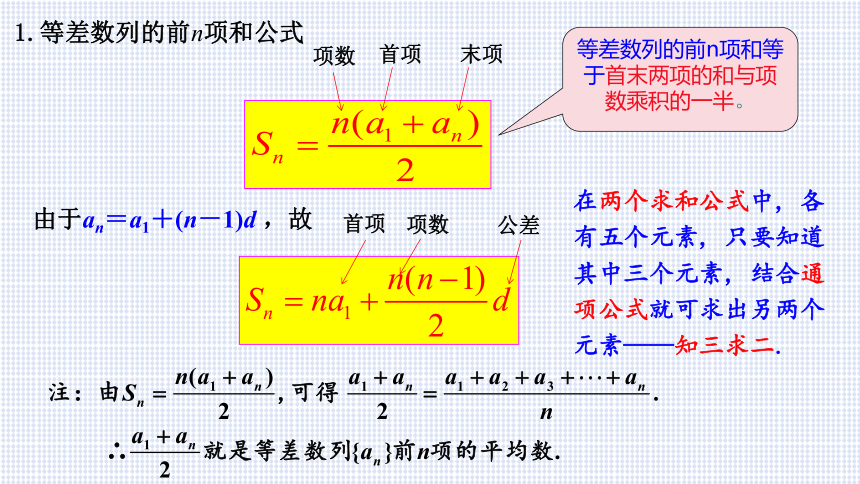
1.等差数列的前n项和公式
首项
项数
公差
等差数列的前n项和等于首末两项的和与项数乘积的一半。
在两个求和公式中, 各有五个元素, 只要知道其中三个元素, 结合通项公式就可求出另两个元素——知三求二.
由于an=a1+(n-1)d ,故
等差数列{an}的相关公式及性质:
三、典型例题1 与等差数列前n项和有关的计算问题
例1 已知数列{an}是等差数列.
(4)已知一个等差数列{an}前10项的和是310,前20项的和是1220. 求这个等差数列的首项和公差.
(4)
二、引导探究2——等差数列的前n项和的性质
已知等差数列 的前 项和为 ,公差为 .
三、典型例题2 等差数列前n项和性质的应用
二、引导探究3——等差数列前n项和的函数形式
当d=0即0时,Sn的图象是一条直线上的均匀分布的点.
当d≠0即0 时,是关于n的二次函数 ,点(n, )在二次函数的图象上,因此当d≠0时,Sn的图象是一条过坐标原点的抛物线上孤立的点.
常数列
情形1:当a1>0,d<0 时,Sn的图象是一条开口向下的过坐标原点的抛物线上孤立的点.
Sn
n
O
1
求等差数列的前n项和最值的两种常用方法
方法一:前n项和公式法求最值
情形2:当a1<0,d>0 时,Sn的图象是一条开口向上的过坐标原点的抛物线上孤立的点.
Sn
n
O
1
方法二:通项公式法求最值
情形1:当a1>0,d<0时,
数列前面有若干项为正, 此时所有非负项的和为Sn的最大值.
此时由an≥0且an+1≤0求n的值
情形2: 当a1<0,d>0时,
数列前面有若干项为负, 此时所有非正项的和为Sn的最小值.
此时由an≤0 且an+1 ≥ 0求n的值
注意:当数列的项中有数值为0时,n应有两解.
三、典型例题3 等差数列前n项的最值问题
C
D
方法总结
四、课堂小结
第四章 数列
4.2.2 等差数列的前n项和
一、课题导入
1. 等差数列定义:
2. 等差数列通项公式:
(2) an=am+(n-m)d .
(3) an=pn+q (p、q是常数)
(1) an=a1+(n-1)d (n≥1).
an-an-1 =d (n≥2)
或 an+1-an =d.
3. 几种计算公差d 的方法:
4. 等差中项
m+n=p+q am+an=ap+aq .
5. 等差数列的性质
d=an-an-1 (n≥2)
二、引导探究1——等差数列的前n项和
据说,200多年前,高斯的算术老师提出了下面的问题:1+2+3+---+99+100=
当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面的方法迅速算出了正确答案,那他是怎么算的呢?
问题:计算1+2+ +100=?
1+2+3+…+50+51+…+98+99+100=
5050
50对
101
101
101
101
思考 你能用高斯的方法求1+2+ +100+101吗
(1+ 101)+(1+100)+ + (50+52)+51=102×50+51= 5151.
或(0+ 101)+(1+100)+ + (50+51)=101×51= 5151.
首尾配对相加法
n + (n-1) + (n-2) +…+ 2 +1
那么,对一般的等差数列,如何求它的前n项和呢?
分析:这其实是求一个具体的等差数列前n项和.
①
②
这种求和方法叫倒序相加法
已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .
如何才能将等式的右边化简?
①
②
项数
首项
末项
1.等差数列的前n项和公式
首项
项数
公差
等差数列的前n项和等于首末两项的和与项数乘积的一半。
在两个求和公式中, 各有五个元素, 只要知道其中三个元素, 结合通项公式就可求出另两个元素——知三求二.
由于an=a1+(n-1)d ,故
等差数列{an}的相关公式及性质:
三、典型例题1 与等差数列前n项和有关的计算问题
例1 已知数列{an}是等差数列.
(4)已知一个等差数列{an}前10项的和是310,前20项的和是1220. 求这个等差数列的首项和公差.
(4)
二、引导探究2——等差数列的前n项和的性质
已知等差数列 的前 项和为 ,公差为 .
三、典型例题2 等差数列前n项和性质的应用
二、引导探究3——等差数列前n项和的函数形式
当d=0即0时,Sn的图象是一条直线上的均匀分布的点.
当d≠0即0 时,是关于n的二次函数 ,点(n, )在二次函数的图象上,因此当d≠0时,Sn的图象是一条过坐标原点的抛物线上孤立的点.
常数列
情形1:当a1>0,d<0 时,Sn的图象是一条开口向下的过坐标原点的抛物线上孤立的点.
Sn
n
O
1
求等差数列的前n项和最值的两种常用方法
方法一:前n项和公式法求最值
情形2:当a1<0,d>0 时,Sn的图象是一条开口向上的过坐标原点的抛物线上孤立的点.
Sn
n
O
1
方法二:通项公式法求最值
情形1:当a1>0,d<0时,
数列前面有若干项为正, 此时所有非负项的和为Sn的最大值.
此时由an≥0且an+1≤0求n的值
情形2: 当a1<0,d>0时,
数列前面有若干项为负, 此时所有非正项的和为Sn的最小值.
此时由an≤0 且an+1 ≥ 0求n的值
注意:当数列的项中有数值为0时,n应有两解.
三、典型例题3 等差数列前n项的最值问题
C
D
方法总结
四、课堂小结
