几何综合测试(含答案)
图片预览


文档简介
几何综合测试
(时间:100分钟 总分:100分)
一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是符合题目要求的)
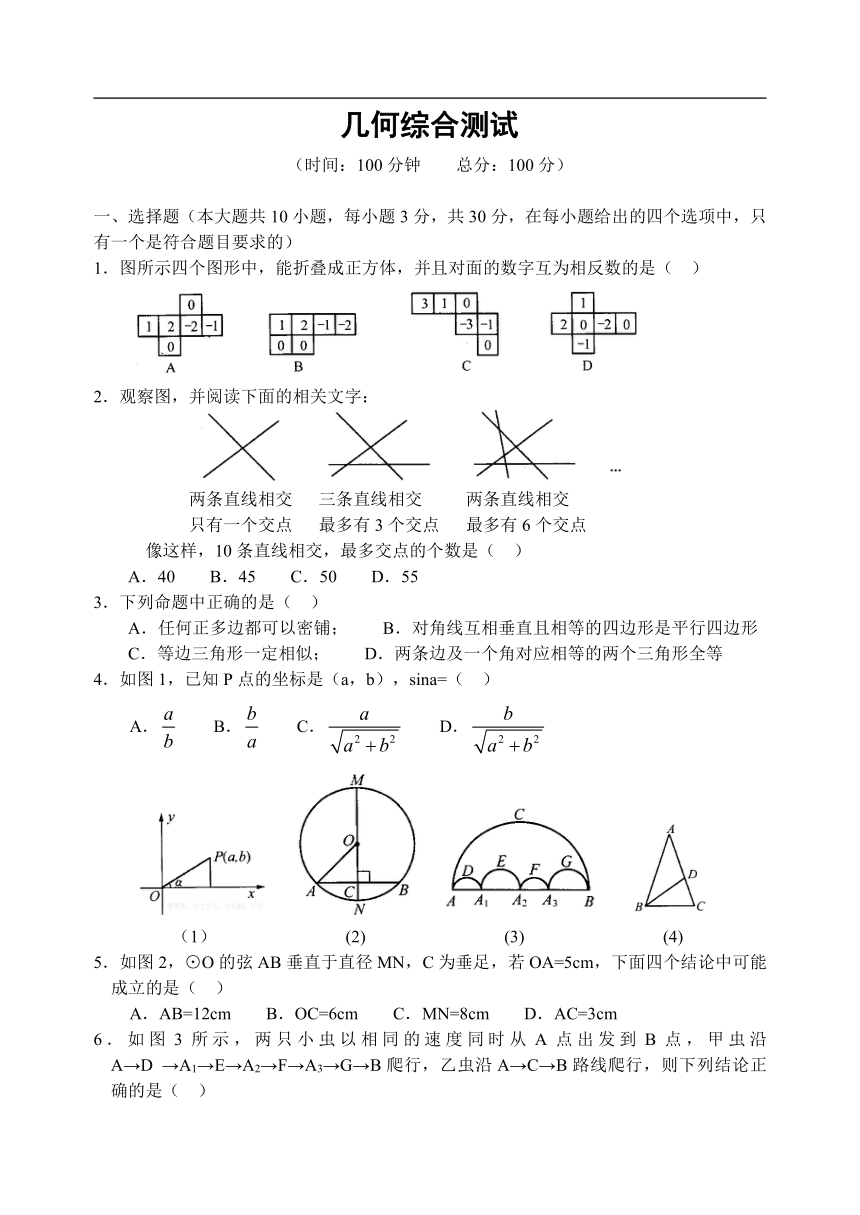
1.图所示四个图形中,能折叠成正方体,并且对面的数字互为相反数的是( )
2.观察图,并阅读下面的相关文字:
两条直线相交 三条直线相交 两条直线相交
只有一个交点 最多有3个交点 最多有6个交点
像这样,10条直线相交,最多交点的个数是( )
A.40 B.45 C.50 D.55
3.下列命题中正确的是( )
A.任何正多边都可以密铺; B.对角线互相垂直且相等的四边形是平行四边形
C.等边三角形一定相似; D.两条边及一个角对应相等的两个三角形全等
4.如图1,已知P点的坐标是(a,b),sina=( )
A. B. C. D.
(1) (2) (3) (4)
5.如图2,⊙O的弦AB垂直于直径MN,C为垂足,若OA=5cm,下面四个结论中可能成立的是( )
A.AB=12cm B.OC=6cm C.MN=8cm D.AC=3cm
6.如图3所示,两只小虫以相同的速度同时从A点出发到B点,甲虫沿A→D→A1→E→A2→F→A3→G→B爬行,乙虫沿A→C→B路线爬行,则下列结论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B点 D.无法确定
7.如图4,等腰△ABC的顶角∠A=36°,BD平分∠ABC交AC于点D,则下列结论不成立的是( )
A.BC=BD=AD B.BC2=DC·AC
C.△ABC三边之比为1:1: D.BC= AC
8.如图5,△ABP与△DCP是两个全等的等边三角形,且PA⊥PD,有下列四个结论:①∠PBC=15°;②AD∥BC;③直线PC⊥AB;④四边形ABCD是轴对称图形,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
(5) (6) (7) (8)
9.如图6,在四边形ABCD中,E是AB上一点,EC∥AD,DE∥BC,若S△BEC=1,S△ADE=3,则AD:CE等于( )
A. B. C. D.3
10.如图7,矩形纸片ABCD中,AD=9cm,AB=3cm,将其折叠,使点B和D重合, 那么折叠后DE的长是( )
A.4cm B.5cm C.3cm D.以上都不正确
二、填空题(本大题共8小题,每小题3分,共24分)
11.如图8,将书页斜折过去,使角顶点A落在A′处,BC为折痕,BD为∠A′BE的平分线,则∠CBD的度数是________.
12.在△ABC中,AB=6,BC=8,∠BAC=80°,如果把△ABC绕点A按顺时针方向旋转35°至△ADE位置(如图9所示),则DE=_______,∠DAC=________.
(9) (10) (11) (12)
13.小明站在镜子前,看见其上衣上的数字代码为“”,则他球衣上的正确号码应是_______.
14.已知三条线段长分别为1,2,4,请你再写出一条线段长,使之与前面的三条线段能够组成一个比例式,则你写出的线段长为________.
15.如图10,BE是△ABC的角平分线,且DE∥BC,如果DE=3cm,则BD=______.
16.已知正方形ABCD的边长为1,E为CD的中点,P是正方形ABCD边上一个动点,动点P从A点出发沿A→B→C→E运动,到达E,若点P经过的路程为自变量x,△APE的面积为函数y,则当y= 时,x的值等于________.
17.如图11,在边长为6的菱形ABCD中,∠BAD=60°,E为AB的中点,F是AC上一动点,则EF+BF的最小值为________.
18.如图12,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE=_________.
三、解答题(本大题共46分,19~23每题6分,24题、25题每题8分,解答题应写出文字说明、证明过程或演算步骤)
19.如图,正方形ABCD中,E、F是对角线AC上的两点,AE=CF,请猜想,四边形BFDE是什么样的四边形,并说明你的理由.
20.如图所示,四边形ABCD是正方形,△ADE旋转后能与△ABF重合.
(1)问旋转了多少度;
(2)连结EF,则△AEF是怎样的三角形.
21.在梯形ABCD中,AB∥CD,AD=2,CD=BC=2,∠A=30°,∠B=60°,求AB和梯形的面积.
22.如图,河的两岸各有一根电线杆A、B,怎样在河的一边测得A、B间的距离,请设计一套方案,并说明你设计的依据.
23.某乡薄铁厂的王师傅要在长为25cm,宽为18cm的薄铁板上裁出一个最大的圆和两个尽可能大的小圆,他先画出了如的草图,但他在求小圆的半径时,遇到了困难,请你帮助王师傅计算出这两个小圆的半径.
24.如图,A、B是直线L上的两点,AB=4厘米,过L外一点作CD∥L,射线BC与L所成的锐角∠1=60°,线段BC=2厘米,动点P、Q分别从B、C同时出发,P以每秒1厘米的速度沿由B向C的方向运动,Q以每秒2厘米的速度沿由C向D的方向运动.设P、Q运动的时间为t(秒),当t>2,PA交CD于E.
(1)用含t的代数式分别表示CE和QE的长.
(2)求△APQ的面积S与t的函数关系式.
(3)当QE恰好平分△APQ的面积时,QE的长是多少厘米?
25.已知:如图,A、K为⊙O上的两点,直线FN⊥MA,垂足为N,FN切⊙O于点F,∠AOK=2∠MAK.
(1)求证:MN是⊙O的切线.
(2)若点B为⊙O上一动点,BO的延长线交⊙O于点C,交NF于点D,连结AC并延长交NF于点E,当FD=2ED时,求∠AEN的余切值.
答案:
一、选择题
1.D 2.B 3.C 4.D 5.D 6.C 7.C 8.D 9.C 10.B
二、填空题
11.90° 12.8,45° 13.26 14.8,0.5等 15.3cm 16.或 17.3 18.
三、解答题
19.解:连结BD交AC于点O,四边形ABCD是平行四边形BO=DO,AO=CD.由于AE=CF,故OE=OF,∴四边形DEBF是平行四边形.又可证△AEB≌△AED,∴BE=DE.故DEBF是菱形.
20.解:(1)旋转了90°.(2)△AEF是等腰直角三角形.
21.解:过点D作DE∥BC,由AB∥CD,可知四边形BCDE是平行四边形.
故DE=BC=2.∠ADE=90°.
在Rt△ADE中,AE===4,
故AB=BE+AE=6.
过点D作DF⊥AB,则DF=AD·sin30°=2,故S梯=×(2+6)×=4.
22.解:利用相似三角形设计.
23.解:连结⊙O1、⊙O2、O1O2,过点O作OA⊥O1O2于A,
则在Rt△OO1A中,OO1=9+r,OA=25-r-9=16-r,O1A==9-r.
由勾股定理,得(16-r)2+(9-r)2=(9+r)2.
解得r1=4,r2=64(舍).
故两个小圆的半径为4.
24.解:(1)依题有BP=t,CQ=2t,PC=t-2.∵EC∥AB,
∴△PEC∽△PAB,∴.
∴EC=,QE=QC-EC=2t-=.
(2)作PF⊥L于F,则PF=t,∴S=QE·PF=(t2-2t+4).
(3)此时,C为PB的中点,则t-2=2,∴t=4,∴QE=6厘米.
25.(1)证明:延长AO交⊙O于点G,连结KG,
MN是⊙O的切线.
A点在⊙O上
(2)解:连结OF,AB.
∵BC为⊙O的直径,∴∠BAC=90°,∵FN⊥MA于N,
∴∠ANE=90°,∵MN是⊙O的切线,∴∠NAE=∠B.
∴∠ACB=∠AEN.又∵∠ACO=∠DCE,∴∠DCE=∠DEC.
∴DC=DE.∵NF切⊙O于F,∴∠OFN=90°.
又∵∠NAO=90°,∴四边形AOFN是矩形.
∵OA=OF,∴矩形AOFN是正方形.
∴AN=NF=OF.∵NF切⊙O于F,∴FD2=DC·DB.
设⊙O的半径为r,DE=x,∵FD=2ED,
∴(2x)2=x(x+2r),解得x=r.
在△AEN中,∠ANE=90°,cot∠AEN=.毛
(时间:100分钟 总分:100分)
一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是符合题目要求的)
1.图所示四个图形中,能折叠成正方体,并且对面的数字互为相反数的是( )
2.观察图,并阅读下面的相关文字:
两条直线相交 三条直线相交 两条直线相交
只有一个交点 最多有3个交点 最多有6个交点
像这样,10条直线相交,最多交点的个数是( )
A.40 B.45 C.50 D.55
3.下列命题中正确的是( )
A.任何正多边都可以密铺; B.对角线互相垂直且相等的四边形是平行四边形
C.等边三角形一定相似; D.两条边及一个角对应相等的两个三角形全等
4.如图1,已知P点的坐标是(a,b),sina=( )
A. B. C. D.
(1) (2) (3) (4)
5.如图2,⊙O的弦AB垂直于直径MN,C为垂足,若OA=5cm,下面四个结论中可能成立的是( )
A.AB=12cm B.OC=6cm C.MN=8cm D.AC=3cm
6.如图3所示,两只小虫以相同的速度同时从A点出发到B点,甲虫沿A→D→A1→E→A2→F→A3→G→B爬行,乙虫沿A→C→B路线爬行,则下列结论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B点 D.无法确定
7.如图4,等腰△ABC的顶角∠A=36°,BD平分∠ABC交AC于点D,则下列结论不成立的是( )
A.BC=BD=AD B.BC2=DC·AC
C.△ABC三边之比为1:1: D.BC= AC
8.如图5,△ABP与△DCP是两个全等的等边三角形,且PA⊥PD,有下列四个结论:①∠PBC=15°;②AD∥BC;③直线PC⊥AB;④四边形ABCD是轴对称图形,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
(5) (6) (7) (8)
9.如图6,在四边形ABCD中,E是AB上一点,EC∥AD,DE∥BC,若S△BEC=1,S△ADE=3,则AD:CE等于( )
A. B. C. D.3
10.如图7,矩形纸片ABCD中,AD=9cm,AB=3cm,将其折叠,使点B和D重合, 那么折叠后DE的长是( )
A.4cm B.5cm C.3cm D.以上都不正确
二、填空题(本大题共8小题,每小题3分,共24分)
11.如图8,将书页斜折过去,使角顶点A落在A′处,BC为折痕,BD为∠A′BE的平分线,则∠CBD的度数是________.
12.在△ABC中,AB=6,BC=8,∠BAC=80°,如果把△ABC绕点A按顺时针方向旋转35°至△ADE位置(如图9所示),则DE=_______,∠DAC=________.
(9) (10) (11) (12)
13.小明站在镜子前,看见其上衣上的数字代码为“”,则他球衣上的正确号码应是_______.
14.已知三条线段长分别为1,2,4,请你再写出一条线段长,使之与前面的三条线段能够组成一个比例式,则你写出的线段长为________.
15.如图10,BE是△ABC的角平分线,且DE∥BC,如果DE=3cm,则BD=______.
16.已知正方形ABCD的边长为1,E为CD的中点,P是正方形ABCD边上一个动点,动点P从A点出发沿A→B→C→E运动,到达E,若点P经过的路程为自变量x,△APE的面积为函数y,则当y= 时,x的值等于________.
17.如图11,在边长为6的菱形ABCD中,∠BAD=60°,E为AB的中点,F是AC上一动点,则EF+BF的最小值为________.
18.如图12,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE=_________.
三、解答题(本大题共46分,19~23每题6分,24题、25题每题8分,解答题应写出文字说明、证明过程或演算步骤)
19.如图,正方形ABCD中,E、F是对角线AC上的两点,AE=CF,请猜想,四边形BFDE是什么样的四边形,并说明你的理由.
20.如图所示,四边形ABCD是正方形,△ADE旋转后能与△ABF重合.
(1)问旋转了多少度;
(2)连结EF,则△AEF是怎样的三角形.
21.在梯形ABCD中,AB∥CD,AD=2,CD=BC=2,∠A=30°,∠B=60°,求AB和梯形的面积.
22.如图,河的两岸各有一根电线杆A、B,怎样在河的一边测得A、B间的距离,请设计一套方案,并说明你设计的依据.
23.某乡薄铁厂的王师傅要在长为25cm,宽为18cm的薄铁板上裁出一个最大的圆和两个尽可能大的小圆,他先画出了如的草图,但他在求小圆的半径时,遇到了困难,请你帮助王师傅计算出这两个小圆的半径.
24.如图,A、B是直线L上的两点,AB=4厘米,过L外一点作CD∥L,射线BC与L所成的锐角∠1=60°,线段BC=2厘米,动点P、Q分别从B、C同时出发,P以每秒1厘米的速度沿由B向C的方向运动,Q以每秒2厘米的速度沿由C向D的方向运动.设P、Q运动的时间为t(秒),当t>2,PA交CD于E.
(1)用含t的代数式分别表示CE和QE的长.
(2)求△APQ的面积S与t的函数关系式.
(3)当QE恰好平分△APQ的面积时,QE的长是多少厘米?
25.已知:如图,A、K为⊙O上的两点,直线FN⊥MA,垂足为N,FN切⊙O于点F,∠AOK=2∠MAK.
(1)求证:MN是⊙O的切线.
(2)若点B为⊙O上一动点,BO的延长线交⊙O于点C,交NF于点D,连结AC并延长交NF于点E,当FD=2ED时,求∠AEN的余切值.
答案:
一、选择题
1.D 2.B 3.C 4.D 5.D 6.C 7.C 8.D 9.C 10.B
二、填空题
11.90° 12.8,45° 13.26 14.8,0.5等 15.3cm 16.或 17.3 18.
三、解答题
19.解:连结BD交AC于点O,四边形ABCD是平行四边形BO=DO,AO=CD.由于AE=CF,故OE=OF,∴四边形DEBF是平行四边形.又可证△AEB≌△AED,∴BE=DE.故DEBF是菱形.
20.解:(1)旋转了90°.(2)△AEF是等腰直角三角形.
21.解:过点D作DE∥BC,由AB∥CD,可知四边形BCDE是平行四边形.
故DE=BC=2.∠ADE=90°.
在Rt△ADE中,AE===4,
故AB=BE+AE=6.
过点D作DF⊥AB,则DF=AD·sin30°=2,故S梯=×(2+6)×=4.
22.解:利用相似三角形设计.
23.解:连结⊙O1、⊙O2、O1O2,过点O作OA⊥O1O2于A,
则在Rt△OO1A中,OO1=9+r,OA=25-r-9=16-r,O1A==9-r.
由勾股定理,得(16-r)2+(9-r)2=(9+r)2.
解得r1=4,r2=64(舍).
故两个小圆的半径为4.
24.解:(1)依题有BP=t,CQ=2t,PC=t-2.∵EC∥AB,
∴△PEC∽△PAB,∴.
∴EC=,QE=QC-EC=2t-=.
(2)作PF⊥L于F,则PF=t,∴S=QE·PF=(t2-2t+4).
(3)此时,C为PB的中点,则t-2=2,∴t=4,∴QE=6厘米.
25.(1)证明:延长AO交⊙O于点G,连结KG,
MN是⊙O的切线.
A点在⊙O上
(2)解:连结OF,AB.
∵BC为⊙O的直径,∴∠BAC=90°,∵FN⊥MA于N,
∴∠ANE=90°,∵MN是⊙O的切线,∴∠NAE=∠B.
∴∠ACB=∠AEN.又∵∠ACO=∠DCE,∴∠DCE=∠DEC.
∴DC=DE.∵NF切⊙O于F,∴∠OFN=90°.
又∵∠NAO=90°,∴四边形AOFN是矩形.
∵OA=OF,∴矩形AOFN是正方形.
∴AN=NF=OF.∵NF切⊙O于F,∴FD2=DC·DB.
设⊙O的半径为r,DE=x,∵FD=2ED,
∴(2x)2=x(x+2r),解得x=r.
在△AEN中,∠ANE=90°,cot∠AEN=.毛
同课章节目录
