第24章 圆单元检测试题（含答案）

中小学教育资源及组卷应用平台
第二十四章《圆》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分，共30分)
1．如图，∠A是⊙O的圆周角，∠OBC=55°，则∠A=（ ）
A．35° B．45° C．55° D．70°
2．如图，△ABC内接于⊙O，且⊙O的半径为2，若∠ACB＝45°，则AB为（　　）
A．2 B． C．4 D．2
3. 一个圆锥的底面半径是4 cm，其侧面展开图的圆心角是120°，则圆锥的母线长是( )
A．8 cm B．12 cm C．16 cm D．24 cm
4．如图，⊙O的直径CD垂直弦AB于点E，且CE＝2，DE＝8，则BE的长为（　　）
A．2 B．4 C．6 D．8
5．如图，正六边形内接于圆，半径为4，则这个正六边形的边心距为（ ）
A．2 B． C． D．
6．如图， ABCD中，∠C＝110°，AB＝2，以AB为直径的⊙O交BC于点E，则的长为（ ）
A． B． C． D．
7. 若正方形的边长为6，则其外接圆半径与内切圆半径的大小分别为( )
A．6，3 B．3，3 C．6，3 D．6，3
8. 如图，已知OT是Rt△ABO斜边AB上的高线，AO＝BO.以O为圆心，OT为半径的圆交OA于点C，过点C作⊙O的切线CD，交AB于点D.则下列结论中错误的是( )
A．DC＝DT B．AD＝DT C．BD＝BO D．2OC＝5AC
9. 如图，△ABC为等腰直角三角形，∠A＝90°，AB＝AC＝，⊙A与BC相切，则图中阴影部分的面积为( )
A．1－ B．1－ C．1－ D．1－
10. 如图，抛物线y＝x2－4与x轴交于A，B两点，P是以点C(0，3)为圆心，2为半径的圆上的动点，Q是线段PA的中点，连接OQ，则线段OQ的最大值是(　　)
A．3 B. C. D．4
二、填空题(每题3分，共24分)
11. 已知圆锥形工件的底面直径是40 cm，母线长30 cm，其侧面展开图圆心角的度数为________．
12. 如图，△ABC内接于⊙O，∠CAB＝30°，∠CBA＝45°，CD⊥AB于点D，若⊙O的半径为2，则CD的长为_______．
13. 如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆相交于点D，连接BD，BE，CE，若∠CBD＝32°，则∠BEC的度数为_____．
14．线段AD过圆心O，交⊙O于点C、D．∠A＝24°，AE交⊙O于点B，且CD＝2AB，则∠EOD＝　 　．
15．如图，在半径为的⊙O中，AB，CD是互相垂直的两条弦，垂足为P，且AB＝CD＝4，则OP的长为　 　．
16．如图，AB、AC是⊙O的两条弦，过点B的切线与半径OC的延长线交于点D，若∠D=40 ，则∠A的度数为________．
17．如图，在圆内接四边形ABCD中，若∠C＝80°，则∠A等于___．
18．在边长为的正方形OABC中，D为边BC上一点，且CD＝1，以O为圆心，OD为半径作圆，分别与OA、OC的延长线交于点E、F，则阴影部分的面积为__．
19．如图，在半径为的中，弦长．求：
（1）的度数；（2）点O到的距离．
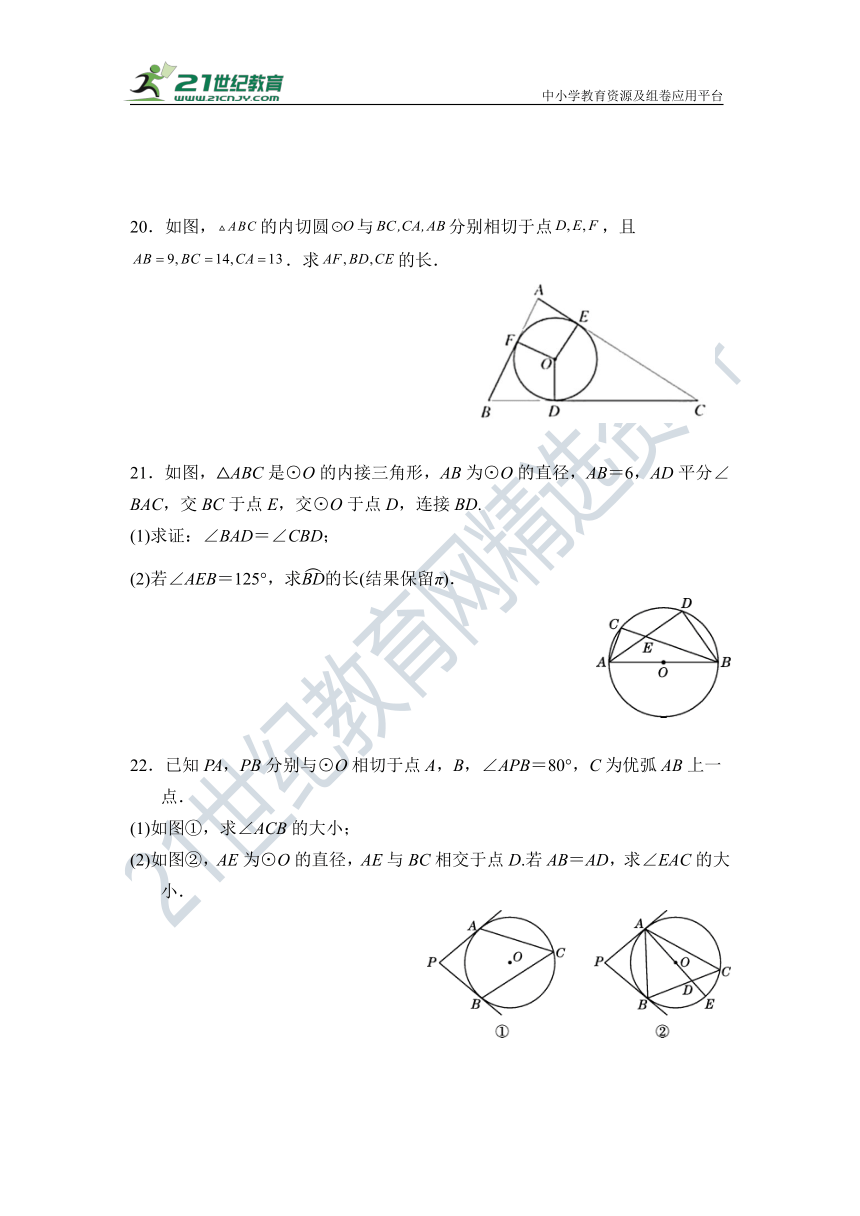
20．如图，的内切圆与分别相切于点，且．求的长．
21．如图，△ABC是⊙O的内接三角形，AB为⊙O的直径，AB＝6，AD平分∠
BAC，交BC于点E，交⊙O于点D，连接BD.
(1)求证：∠BAD＝∠CBD；
(2)若∠AEB＝125°，求的长(结果保留π)．
22．已知PA，PB分别与⊙O相切于点A，B，∠APB＝80°，C为优弧AB上一点．
(1)如图①，求∠ACB的大小；
(2)如图②，AE为⊙O的直径，AE与BC相交于点D.若AB＝AD，求∠EAC的大小．
23．如图，在Rt△ABC中，∠ACB＝90°，以AB为直径作⊙O，过点C作直线CD交AB的延长线于点D，使∠BCD＝∠A.
(1)求证：CD为⊙O的切线；
(2)若DE平分∠ADC，且分别交AC，BC于点E，F，当CE＝2时，求EF的长．
24.已知∠MPN的两边分别与⊙O相切于点A，B，⊙O的半径为r.
(1)如图①，点C在点A，B之间的优弧上，∠MPN＝80°，求∠ACB的度数．
(2)如图②，点C在圆上运动，当PC最大时，要使四边形APBC为菱形，∠APB的度数应为多少？请说明理由．
(3)若PC交⊙O于点D，求第(2)问中对应的阴影部分的周长(用含r的式子表示)．
参考答案
一、选择题(每题3分，共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B B D B D D C C
二、填空题(每题3分，共24分)
11．60
12．215
13．15°或75°
14．解：连接OB，∵AB＝OC＝OB，
∴∠BOC＝∠A＝24°，
∠EBO＝2∠A＝48°，
∵OE＝OB
∴∠E＝∠EBO＝48°，
∴∠EOD＝∠A+∠E＝24°+48°＝72°．
故答案是：72°．
15．解：作OE⊥AB于E，OF⊥CD于F，连接OD、OB，
则AE＝BE＝AB＝2，DF＝CF＝CD＝2，
在Rt△OBE中，OB＝，BE＝2，
∴OE＝＝1，
同理可得OF＝1，
∵AB⊥CD，OE⊥AB，OF⊥CD，
∴四边形OEPF为矩形，
∵OE＝OF＝1，
∴四边形OEPF为正方形，
∴OP＝OE＝，
故答案为：．
16．25°
17．100°
18．3﹣﹣
三.解答题(共46分,19题6分，20 ---24题8分)
19．
解：（1）∵OA，OB是⊙O的半径，
∴OA＝OB＝50mm，
又∵AB＝50mm，
∴OA＝OB＝AB，
∴△AOB是等边三角形，
∴∠AOB＝60°．　　
（2）过点O作OC⊥AB，垂足为点C，如图所示，
由垂径定理得AC＝CB＝AB＝25mm，
在Rt△OAC中OC2＝OA2－AC2＝502－252＝252×3，
∴OC＝＝25（mm），
即点O到AB的距离是25mm．
20．
解：∵△ABC 的内切圆⊙O与BC,CA,AB分别相切于点D,E,F，
设，则，
，
．
由，可得
．
解得．
因此．
21．(1)证明：∵AD平分∠BAC，
∴∠BAD＝∠CAD.
又∵∠CBD＝∠CAD，
∴∠BAD＝∠CBD.
(2)解：连接OD.
∵∠AEB＝125°，∴∠AEC＝55°.
∵AB为⊙O的直径，
∴∠ACE＝90°.
∴∠CAE＝35°.
∴∠DAB＝35°.
则所对圆心角∠DOB＝70°.
∴的长为＝π.
22．解：(1)连接OA，OB.
∵PA，PB是⊙O的切线，
∴∠OAP＝∠OBP＝90°.
∴∠AOB＝360°－90°－90°－80°＝100°.
∴∠ACB＝∠AOB＝50°.
(2)连接CE.
∵AE为⊙O的直径，∴∠ACE＝90°.
∵∠ACB＝50°，
∴∠BCE＝90°－50°＝40°.
∴∠BAE＝∠BCE＝40°.
∵AB＝AD，∴∠ABD＝∠ADB＝70°.
∴∠EAC＝∠ADB－∠ACB＝20°.
23. 解：(1)证明：连接OC，∵AB为⊙O的直径，∠ACB＝90°，∴点C在⊙O上，∠A＋∠ABC＝90°，又∵OC＝OB，∴∠ABC＝∠OCB，∵∠BCD＝∠A，∴∠BCD＋∠OCB＝90°，即∠OCD＝90°，∵OC是圆O的半径，∴CD是⊙O的切线
(2)∵DE平分∠ADC，∴∠CDE＝∠ADE，又∵∠BCD＝∠A，∴∠A＋∠ADE＝∠BCD＋∠CDF，即∠CEF＝∠CFE，∵∠ACB＝90°，CE＝2，∴CE＝CF＝2，∴EF＝＝2
24. (1)解：如图①，连接OA，OB.∵PA，PB为⊙O的切线，∴∠PAO＝∠PBO＝90°.∵∠APB＋∠PAO＋∠PBO＋∠AOB＝360°，∴∠APB＋∠AOB＝180°.∵∠APB＝80°，∴∠AOB＝100°.∴∠ACB＝50°.
(2)当∠APB＝60°时，四边形APBC为菱形．理由如下：如图②，连接OA，OB.由(1)可知∠AOB＋∠APB＝180°.∵∠APB＝60°，∴∠AOB＝120°.∴∠ACB＝60°＝∠APB.∵点C运动到如图所示的位置时，PC距离最大，∴PC经过圆心．∵PA，PB为⊙O的切线，∴PA＝PB，∠APC＝∠BPC＝30°.又∵PC＝PC，∴△APC≌△BPC(SAS)．∴∠ACP＝∠BCP＝30°，AC＝BC.∴∠APC＝∠ACP＝30°.∴AP＝AC.∴AP＝AC＝PB＝BC.∴四边形APBC是菱形．
(3)解：∵⊙O的半径为r，∴OA＝r，OP＝2r. ∴AP＝r，PD＝r.∵∠AOP＝90°－∠APO＝60°，∴的长为＝r.∴阴影部分的周长＝PA＋PD＋的长＝r＋r＋r＝r.