24.1 测量分层练习(含答案)
文档属性
| 名称 | 24.1 测量分层练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 535.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 08:04:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.1测量
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,该同学的身高为1.7m,则树高为( )m.
A.3.4 B.5.1 C.6.8 D.8.5
2.如图,小明为了测量大楼MN的高度,在离N点30米放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度是( )
A.32米 B.米 C.36米 D.米
3.已知:如图,某学生想利用标杆测量一棵大树的高度,如果标杆EC的高为 1.6 m,并测得BC=2.2 m ,CA=0.8 m, 那么树DB的高度是( )
A.6 m B.5.6 m C.5.4 m D.4.4 m
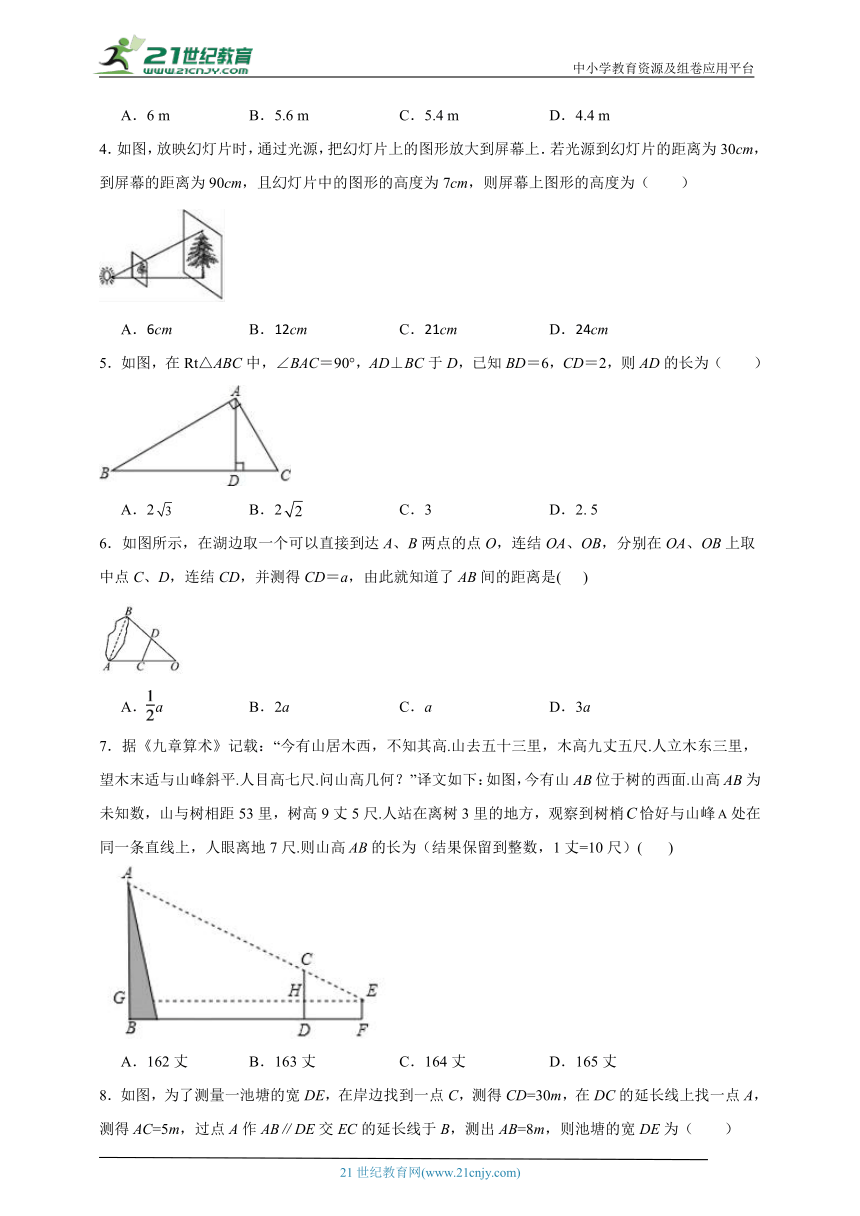
4.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm,到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为( )
A.6cm B.12cm C.21cm D.24cm
5.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,已知BD=6,CD=2,则AD的长为( )
A.2 B.2 C.3 D.2. 5
6.如图所示,在湖边取一个可以直接到达A、B两点的点O,连结OA、OB,分别在OA、OB上取中点C、D,连结CD,并测得CD=a,由此就知道了AB间的距离是( )
A.a B.2a C.a D.3a
7.据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺.人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何?”译文如下:如图,今有山位于树的西面.山高为未知数,山与树相距53里,树高9丈5尺.人站在离树3里的地方,观察到树梢恰好与山峰处在同一条直线上,人眼离地7尺.则山高的长为(结果保留到整数,1丈=10尺)( )
A.162丈 B.163丈 C.164丈 D.165丈
8.如图,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE交EC的延长线于B,测出AB=8m,则池塘的宽DE为( )
A.32m B.36m C.48m D.56m
9.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=4,AC=3,则BD为( )
A.1.8 B.3.2 C.2.4 D.5
10.为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.如图,通过测量,得到AC长160 m,BC长128 m,则从点A穿过湖到点B的距离是( )
A.48 m B.90 m C.96 m D.69 m
二、填空题
11.如图,小明从路灯下向前走了5米,发现自己在地面上的影子长DE是2米,如果小明的身高为1.6米,那么路灯离地面的高度AB是 米.
12.如图,一根长20 m的笔直竹竿AB顶端刚好搭在墙头AC上,墙根C到竹竿末端B的距离为16 m,则墙头的高度为 m.
13.如图,A,B两地之间有一池塘,要测量A,B两地之间的距离,选择一点O连接AO并延长到点C,使OC=AO.连接BO并延长到点D,使OD=BO,测得C、D间距离为30米,则A,B两地之间的距离为 .
14.如图,直立在点B处的标杆AB=2.5m,站立在点F处的观测者从点E看到标杆顶A,树顶C在同一直线上(点F,B,D也在同一直线上).已知BD=10m,FB=3m,人的高度EF=1.7 m,则树高DC是 .(精确到0.1 m)
15.如图,2m长的竹竿竖直放置,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为 米.
16.如图,在Rt△ABC中,∠A=90°,AB=AC=8,点E为AC的中点,点F在底边BC上,且FE⊥BE,则CF长 .
17.如图,一棵大树被风吹断,已知折断处距地面5米,树的折断部分与地面成45°的角,这棵大树有 米.
18.两个任意大小的正方形,都可以适当剪开,拼成一个较大的正方形,如用两个边长分别为,的正方形拼成一个大正方形.图中的斜边的长等于 (用,的代数式表示).
19.如图,有一段防洪大堤,其横断面为梯形,,斜坡的坡度,斜坡的坡度,大堤顶宽为,为了增加抗洪能力,现将大堤加高,加高部分的横断面为梯形,,点、分别在,的延长线上,当新大堤顶宽为时,大堤加高 米.
20.为了测量校园水平地面上一棵不可攀爬的树的高度,小文同学做了如下的探索:根据物理学中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在合适的位置,刚好能在镜子里看到树梢顶点,此时小文与平面镜的水平距离为2.0米,树的底部与平面镜的水平距离为8.0米,若小文的眼睛与地面的距离为1.6米,则树的高度约为 米.(注:反射角等于入射角)
三、解答题
21.如图所示,AD、BC为两路灯,身高相同的小明、小亮站在两路灯杆之间,两人相距6.5m,小明站在P处,小亮站在Q处,小明在路灯C下的影长为2m,已知小明身高1.8m,路灯BC高9m.
①计算小亮在路灯D下的影长;
②计算建筑物AD的高.
22.如图,已知△ABC,∠ACB=90°
(1)求作AB边上的高CD.(尺规作图,保留作图痕迹,不写作法)
(2)若AD=2, BD=4,求高CD的长.
23.如图,在距树AB 18米的地面上平放着一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰好看见树顶A,若人眼距地面1.4米,求树AB的高.
24.如图,一人拿着一支刻有厘米分划的小尺,他站在距电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上约12个分划恰好遮住电线杆,已知臂长约60厘米.求电线杆的高.
25.如图,为了估算河的宽度,我们可以在河对岸选定一点,再在河的这一边选定点和点,使得,然后选定点,使,确定与的交点,若测得米,米,米,请你求出小河的宽度是多少米?
参考答案:
1.B
2.A
3.A
4.C
5.A
6.B
7.D
8.C
9.B
10.C
11.5.6
12.12
13.60m.
14.5.2m
15.6
16.
17.(5+5)
18.
19.1.1
20.6.4
21.①;②.
22.(1)略;(2)
23.树高12米.
24.电线杆的高为6米.
25.小河的宽度是210米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.1测量
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,该同学的身高为1.7m,则树高为( )m.
A.3.4 B.5.1 C.6.8 D.8.5
2.如图,小明为了测量大楼MN的高度,在离N点30米放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度是( )
A.32米 B.米 C.36米 D.米
3.已知:如图,某学生想利用标杆测量一棵大树的高度,如果标杆EC的高为 1.6 m,并测得BC=2.2 m ,CA=0.8 m, 那么树DB的高度是( )
A.6 m B.5.6 m C.5.4 m D.4.4 m
4.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm,到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为( )
A.6cm B.12cm C.21cm D.24cm
5.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,已知BD=6,CD=2,则AD的长为( )
A.2 B.2 C.3 D.2. 5
6.如图所示,在湖边取一个可以直接到达A、B两点的点O,连结OA、OB,分别在OA、OB上取中点C、D,连结CD,并测得CD=a,由此就知道了AB间的距离是( )
A.a B.2a C.a D.3a
7.据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺.人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何?”译文如下:如图,今有山位于树的西面.山高为未知数,山与树相距53里,树高9丈5尺.人站在离树3里的地方,观察到树梢恰好与山峰处在同一条直线上,人眼离地7尺.则山高的长为(结果保留到整数,1丈=10尺)( )
A.162丈 B.163丈 C.164丈 D.165丈
8.如图,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE交EC的延长线于B,测出AB=8m,则池塘的宽DE为( )
A.32m B.36m C.48m D.56m
9.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=4,AC=3,则BD为( )
A.1.8 B.3.2 C.2.4 D.5
10.为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.如图,通过测量,得到AC长160 m,BC长128 m,则从点A穿过湖到点B的距离是( )
A.48 m B.90 m C.96 m D.69 m
二、填空题
11.如图,小明从路灯下向前走了5米,发现自己在地面上的影子长DE是2米,如果小明的身高为1.6米,那么路灯离地面的高度AB是 米.
12.如图,一根长20 m的笔直竹竿AB顶端刚好搭在墙头AC上,墙根C到竹竿末端B的距离为16 m,则墙头的高度为 m.
13.如图,A,B两地之间有一池塘,要测量A,B两地之间的距离,选择一点O连接AO并延长到点C,使OC=AO.连接BO并延长到点D,使OD=BO,测得C、D间距离为30米,则A,B两地之间的距离为 .
14.如图,直立在点B处的标杆AB=2.5m,站立在点F处的观测者从点E看到标杆顶A,树顶C在同一直线上(点F,B,D也在同一直线上).已知BD=10m,FB=3m,人的高度EF=1.7 m,则树高DC是 .(精确到0.1 m)
15.如图,2m长的竹竿竖直放置,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为 米.
16.如图,在Rt△ABC中,∠A=90°,AB=AC=8,点E为AC的中点,点F在底边BC上,且FE⊥BE,则CF长 .
17.如图,一棵大树被风吹断,已知折断处距地面5米,树的折断部分与地面成45°的角,这棵大树有 米.
18.两个任意大小的正方形,都可以适当剪开,拼成一个较大的正方形,如用两个边长分别为,的正方形拼成一个大正方形.图中的斜边的长等于 (用,的代数式表示).
19.如图,有一段防洪大堤,其横断面为梯形,,斜坡的坡度,斜坡的坡度,大堤顶宽为,为了增加抗洪能力,现将大堤加高,加高部分的横断面为梯形,,点、分别在,的延长线上,当新大堤顶宽为时,大堤加高 米.
20.为了测量校园水平地面上一棵不可攀爬的树的高度,小文同学做了如下的探索:根据物理学中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在合适的位置,刚好能在镜子里看到树梢顶点,此时小文与平面镜的水平距离为2.0米,树的底部与平面镜的水平距离为8.0米,若小文的眼睛与地面的距离为1.6米,则树的高度约为 米.(注:反射角等于入射角)
三、解答题
21.如图所示,AD、BC为两路灯,身高相同的小明、小亮站在两路灯杆之间,两人相距6.5m,小明站在P处,小亮站在Q处,小明在路灯C下的影长为2m,已知小明身高1.8m,路灯BC高9m.
①计算小亮在路灯D下的影长;
②计算建筑物AD的高.
22.如图,已知△ABC,∠ACB=90°
(1)求作AB边上的高CD.(尺规作图,保留作图痕迹,不写作法)
(2)若AD=2, BD=4,求高CD的长.
23.如图,在距树AB 18米的地面上平放着一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰好看见树顶A,若人眼距地面1.4米,求树AB的高.
24.如图,一人拿着一支刻有厘米分划的小尺,他站在距电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上约12个分划恰好遮住电线杆,已知臂长约60厘米.求电线杆的高.
25.如图,为了估算河的宽度,我们可以在河对岸选定一点,再在河的这一边选定点和点,使得,然后选定点,使,确定与的交点,若测得米,米,米,请你求出小河的宽度是多少米?
参考答案:
1.B
2.A
3.A
4.C
5.A
6.B
7.D
8.C
9.B
10.C
11.5.6
12.12
13.60m.
14.5.2m
15.6
16.
17.(5+5)
18.
19.1.1
20.6.4
21.①;②.
22.(1)略;(2)
23.树高12米.
24.电线杆的高为6米.
25.小河的宽度是210米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
