热点18 直角三角形的应用(含答案)
图片预览

文档简介
热点18 直角三角形的应用
(时间:100分钟 总分:100分)
一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是符合题目要求的)
1.如图1,在离地面高度5米处引拉线固定电线杆,拉线和地面成60°,则拉线AC的长为( )
A.5tan60°米 B.米 C.5cot60°米 D.米
(1) (2) (3)
2.直角三角形的斜边与一直角边的比是:1,且较大的锐角为θ,则sinθ等于( )
A. B. C. D.
3.某市在“旧城改造”中计划在市内一块如图2的三角形空地上移植某种草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A.450a元 B.225a元 C.150a元 D.300a元
4.身高相等的三名同学甲、乙、丙参加风筝比赛,三人放出风筝线长,线与地面的夹角如下表(假设风筝线是直的),则三人所放的风筝中( )
同学 甲 乙 丙
放出风筝线长(米) 100m 100m 90m
线与地面夹角 40° 45° 60°
A.甲的最高 B.丙的最高 C.乙的最低 D.丙的最低
5.已知楼房AB高50m,如图3,铁塔塔基距楼房房基间水平距离BD为50m,塔高CD为m.
A.由楼顶望塔顶仰角为60° B.由楼顶望塔基俯角为60°
C.由楼顶望塔顶仰角为30° D.由楼顶望塔基俯角为30°
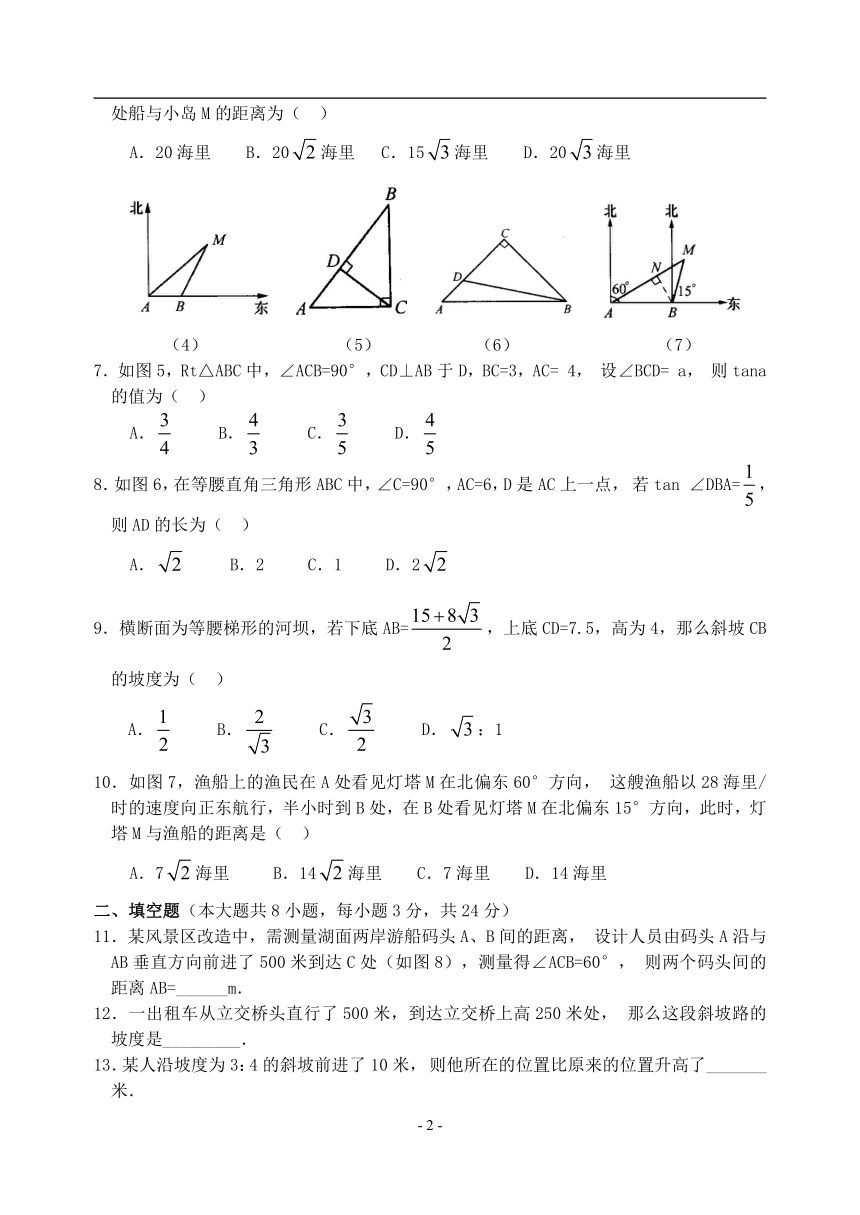
6.上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处(如图4),从A、B两处分别测得小岛M在北偏东45°和北偏东15°,那么B处船与小岛M的距离为( )
A.20海里 B.20海里 C.15海里 D.20海里
(4) (5) (6) (7)
7.如图5,Rt△ABC中,∠ACB=90°,CD⊥AB于D,BC=3,AC=4,设∠BCD=a,则tana的值为( )
A. B. C. D.
8.如图6,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=,则AD的长为( )
A. B.2 C.1 D.2
9.横断面为等腰梯形的河坝,若下底AB=,上底CD=7.5,高为4,那么斜坡CB的坡度为( )
A. B. C. D.:1
10.如图7,渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时到B处,在B处看见灯塔M在北偏东15°方向,此时,灯塔M与渔船的距离是( )
A.7海里 B.14海里 C.7海里 D.14海里
二、填空题(本大题共8小题,每小题3分,共24分)
11.某风景区改造中,需测量湖面两岸游船码头A、B间的距离,设计人员由码头A沿与AB垂直方向前进了500米到达C处(如图8),测量得∠ACB=60°,则两个码头间的距离AB=______m.
12.一出租车从立交桥头直行了500米,到达立交桥上高250米处,那么这段斜坡路的坡度是_________.
13.某人沿坡度为3:4的斜坡前进了10米,则他所在的位置比原来的位置升高了_______米.
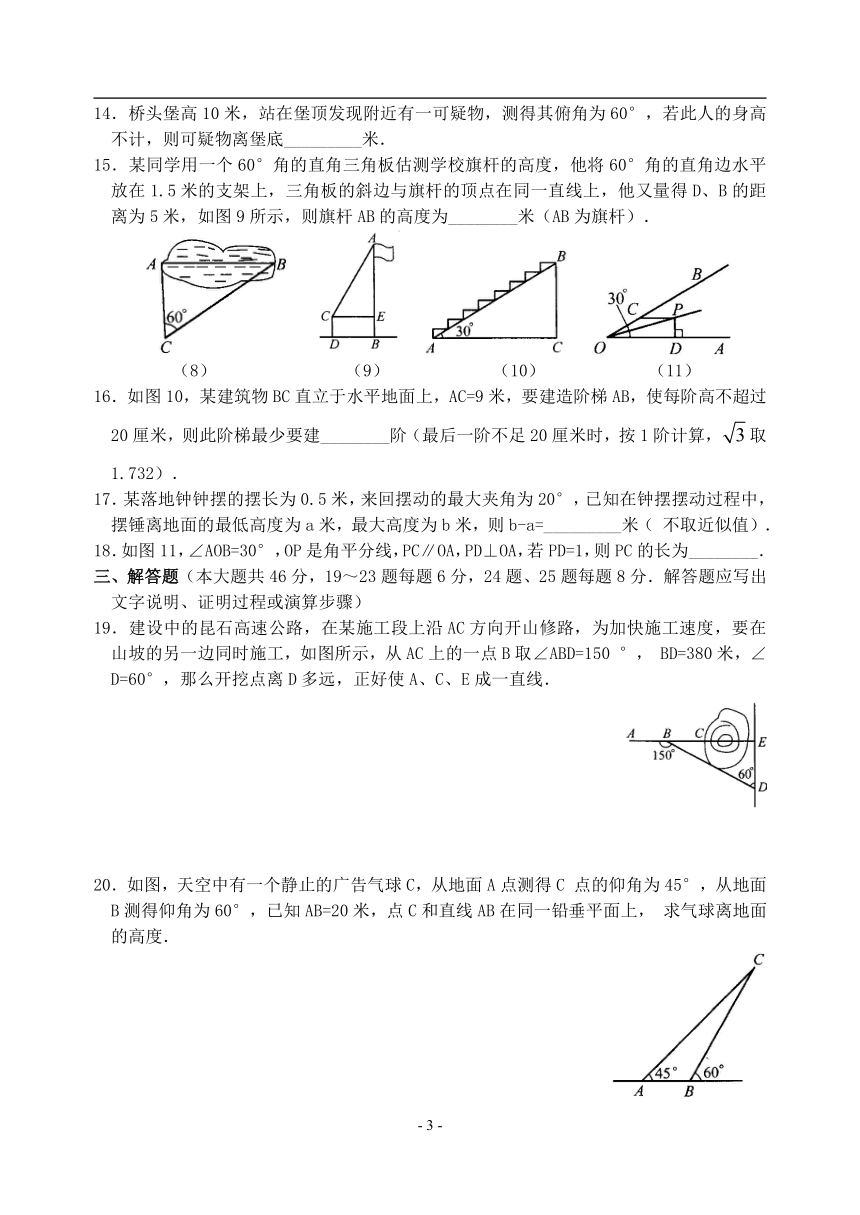
14.桥头堡高10米,站在堡顶发现附近有一可疑物,测得其俯角为60°,若此人的身高不计,则可疑物离堡底_________米.
15.某同学用一个60°角的直角三角板估测学校旗杆的高度,他将60°角的直角边水平放在1.5米的支架上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为5米,如图9所示,则旗杆AB的高度为________米(AB为旗杆).
(8) (9) (10) (11)
16.如图10,某建筑物BC直立于水平地面上,AC=9米,要建造阶梯AB,使每阶高不超过20厘米,则此阶梯最少要建________阶(最后一阶不足20厘米时,按1阶计算,取1.732).
17.某落地钟钟摆的摆长为0.5米,来回摆动的最大夹角为20°,已知在钟摆摆动过程中,摆锤离地面的最低高度为a米,最大高度为b米,则b-a=_________米(不取近似值).
18.如图11,∠AOB=30°,OP是角平分线,PC∥OA,PD⊥OA,若PD=1,则PC的长为________.
三、解答题(本大题共46分,19~23题每题6分,24题、25题每题8分.解答题应写出文字说明、证明过程或演算步骤)
19.建设中的昆石高速公路,在某施工段上沿AC方向开山修路,为加快施工速度,要在山坡的另一边同时施工,如图所示,从AC上的一点B取∠ABD=150°,BD=380米,∠D=60°,那么开挖点离D多远,正好使A、C、E成一直线.
20.如图,天空中有一个静止的广告气球C,从地面A点测得C点的仰角为45°,从地面B测得仰角为60°,已知AB=20米,点C和直线AB在同一铅垂平面上,求气球离地面的高度.
21.某海岛四周18海里内有暗礁,一货轮由西向东航行,见此岛在北偏东60°,行 海里后,见此岛在北偏东30°,货轮沿原方向继续航行,有无触礁危险?
22.如图,在一座山顶B处,用高为1米的测倾器AB量地面C、D两点测得的俯角分别为60°和45°,若已知CD长是20米,求山高BE.
23.如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所学校,AP=160米,假设拖拉机行驶时,周围100米以内会有噪音影响.则当拖拉机以18千米/时的速度在公路MN上行驶时,学校是否会受影响?如果受影响,请计算出学校受影响的时间是多长?如果不受影响请说明理由.
24.如图,甲、乙两只捕捞船同时从A港出海捕鱼,甲船以每小时15千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
(1)甲船从C处追赶上乙船用了多少时间?(2)甲船追赶乙船的速度是多少?
25.如图所示,张琪家居住在甲楼AB,现计划在他家居住的楼前修建一座乙楼CD,楼高约为18米,两楼之间的距离为20米,已知冬天的太阳最低时,光线与水平线的夹角为31°(tan31°取0.600 9,cot31°取1.664).
(1)试求乙楼CD的影子落在甲楼AB上的高BE的长.
(2)若让乙楼的影子刚好不影响甲楼,则两楼之间的距离至少应是多少米?(精确到0.01米)
答案:
一、选择题
1.B 2.D 3.C 4.B 5.C 6.B 7.A 8.B 9.B 10.A
二、填空题
11.500 12. 13.6 14. 15.
16.26 17.(1-cos10°) 18.2
三、解答题
19.解:∵∠ABD=150°,∠D=60°,∴∠BED=90°.
在Rt△BDE中,DE=BD·cos60°=380×=190(米).
20.解:过点C作CD⊥AB于D,则
在Rt△ACD中,AD==CD,
在Rt△BCD中,BD==CD,
∴AB=AD-BD,即20=CD-CD.
解得,CD=(30+10)米,故气球高为(30+10)米.
21.解:如图,由已知得∠AMB=30°=∠BAMBM=
MC=BM·sin60°=×=20>18,
故无触礁危险.
22.解:在Rt△ADE中,DE==AE,
在Rt△ACE中,CE==AE.
而CD=DE-CE即20=AE-AE,解得AE=(30+10)(米).
故BE=(29+10)(米).
23.解:会受影响.如图,作AD⊥MNAD=80<100.AB=AC=100 BC=120.
故受影响时间 =0.4(分)
24.解:(1)过点A作AD⊥BC于D,
由题意易得∠B=30°,∠BAC=105°,∠BCA=45°,AC=30千米,
在Rt△ADC中,CD=AD=AC.cos45°=30千米,
在Rt△ABD中,AB=2AD=60千米,t==4(时).
(2)由(1)知BD=AB·cos30°=30千米,
∴BC=30+30(千米) v==(千米/时).
25.解:(1)tan31°==0.600 9,
故BE=18-12.018=5.982≈5.98(米)
tan31°=FD=,FD≈29.96(米)
故两楼间的距离至少应是29.96米.毛
- 1 -
(时间:100分钟 总分:100分)
一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是符合题目要求的)
1.如图1,在离地面高度5米处引拉线固定电线杆,拉线和地面成60°,则拉线AC的长为( )
A.5tan60°米 B.米 C.5cot60°米 D.米
(1) (2) (3)
2.直角三角形的斜边与一直角边的比是:1,且较大的锐角为θ,则sinθ等于( )
A. B. C. D.
3.某市在“旧城改造”中计划在市内一块如图2的三角形空地上移植某种草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A.450a元 B.225a元 C.150a元 D.300a元
4.身高相等的三名同学甲、乙、丙参加风筝比赛,三人放出风筝线长,线与地面的夹角如下表(假设风筝线是直的),则三人所放的风筝中( )
同学 甲 乙 丙
放出风筝线长(米) 100m 100m 90m
线与地面夹角 40° 45° 60°
A.甲的最高 B.丙的最高 C.乙的最低 D.丙的最低
5.已知楼房AB高50m,如图3,铁塔塔基距楼房房基间水平距离BD为50m,塔高CD为m.
A.由楼顶望塔顶仰角为60° B.由楼顶望塔基俯角为60°
C.由楼顶望塔顶仰角为30° D.由楼顶望塔基俯角为30°
6.上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处(如图4),从A、B两处分别测得小岛M在北偏东45°和北偏东15°,那么B处船与小岛M的距离为( )
A.20海里 B.20海里 C.15海里 D.20海里
(4) (5) (6) (7)
7.如图5,Rt△ABC中,∠ACB=90°,CD⊥AB于D,BC=3,AC=4,设∠BCD=a,则tana的值为( )
A. B. C. D.
8.如图6,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=,则AD的长为( )
A. B.2 C.1 D.2
9.横断面为等腰梯形的河坝,若下底AB=,上底CD=7.5,高为4,那么斜坡CB的坡度为( )
A. B. C. D.:1
10.如图7,渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时到B处,在B处看见灯塔M在北偏东15°方向,此时,灯塔M与渔船的距离是( )
A.7海里 B.14海里 C.7海里 D.14海里
二、填空题(本大题共8小题,每小题3分,共24分)
11.某风景区改造中,需测量湖面两岸游船码头A、B间的距离,设计人员由码头A沿与AB垂直方向前进了500米到达C处(如图8),测量得∠ACB=60°,则两个码头间的距离AB=______m.
12.一出租车从立交桥头直行了500米,到达立交桥上高250米处,那么这段斜坡路的坡度是_________.
13.某人沿坡度为3:4的斜坡前进了10米,则他所在的位置比原来的位置升高了_______米.
14.桥头堡高10米,站在堡顶发现附近有一可疑物,测得其俯角为60°,若此人的身高不计,则可疑物离堡底_________米.
15.某同学用一个60°角的直角三角板估测学校旗杆的高度,他将60°角的直角边水平放在1.5米的支架上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为5米,如图9所示,则旗杆AB的高度为________米(AB为旗杆).
(8) (9) (10) (11)
16.如图10,某建筑物BC直立于水平地面上,AC=9米,要建造阶梯AB,使每阶高不超过20厘米,则此阶梯最少要建________阶(最后一阶不足20厘米时,按1阶计算,取1.732).
17.某落地钟钟摆的摆长为0.5米,来回摆动的最大夹角为20°,已知在钟摆摆动过程中,摆锤离地面的最低高度为a米,最大高度为b米,则b-a=_________米(不取近似值).
18.如图11,∠AOB=30°,OP是角平分线,PC∥OA,PD⊥OA,若PD=1,则PC的长为________.
三、解答题(本大题共46分,19~23题每题6分,24题、25题每题8分.解答题应写出文字说明、证明过程或演算步骤)
19.建设中的昆石高速公路,在某施工段上沿AC方向开山修路,为加快施工速度,要在山坡的另一边同时施工,如图所示,从AC上的一点B取∠ABD=150°,BD=380米,∠D=60°,那么开挖点离D多远,正好使A、C、E成一直线.
20.如图,天空中有一个静止的广告气球C,从地面A点测得C点的仰角为45°,从地面B测得仰角为60°,已知AB=20米,点C和直线AB在同一铅垂平面上,求气球离地面的高度.
21.某海岛四周18海里内有暗礁,一货轮由西向东航行,见此岛在北偏东60°,行 海里后,见此岛在北偏东30°,货轮沿原方向继续航行,有无触礁危险?
22.如图,在一座山顶B处,用高为1米的测倾器AB量地面C、D两点测得的俯角分别为60°和45°,若已知CD长是20米,求山高BE.
23.如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所学校,AP=160米,假设拖拉机行驶时,周围100米以内会有噪音影响.则当拖拉机以18千米/时的速度在公路MN上行驶时,学校是否会受影响?如果受影响,请计算出学校受影响的时间是多长?如果不受影响请说明理由.
24.如图,甲、乙两只捕捞船同时从A港出海捕鱼,甲船以每小时15千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
(1)甲船从C处追赶上乙船用了多少时间?(2)甲船追赶乙船的速度是多少?
25.如图所示,张琪家居住在甲楼AB,现计划在他家居住的楼前修建一座乙楼CD,楼高约为18米,两楼之间的距离为20米,已知冬天的太阳最低时,光线与水平线的夹角为31°(tan31°取0.600 9,cot31°取1.664).
(1)试求乙楼CD的影子落在甲楼AB上的高BE的长.
(2)若让乙楼的影子刚好不影响甲楼,则两楼之间的距离至少应是多少米?(精确到0.01米)
答案:
一、选择题
1.B 2.D 3.C 4.B 5.C 6.B 7.A 8.B 9.B 10.A
二、填空题
11.500 12. 13.6 14. 15.
16.26 17.(1-cos10°) 18.2
三、解答题
19.解:∵∠ABD=150°,∠D=60°,∴∠BED=90°.
在Rt△BDE中,DE=BD·cos60°=380×=190(米).
20.解:过点C作CD⊥AB于D,则
在Rt△ACD中,AD==CD,
在Rt△BCD中,BD==CD,
∴AB=AD-BD,即20=CD-CD.
解得,CD=(30+10)米,故气球高为(30+10)米.
21.解:如图,由已知得∠AMB=30°=∠BAMBM=
MC=BM·sin60°=×=20>18,
故无触礁危险.
22.解:在Rt△ADE中,DE==AE,
在Rt△ACE中,CE==AE.
而CD=DE-CE即20=AE-AE,解得AE=(30+10)(米).
故BE=(29+10)(米).
23.解:会受影响.如图,作AD⊥MNAD=80<100.AB=AC=100 BC=120.
故受影响时间 =0.4(分)
24.解:(1)过点A作AD⊥BC于D,
由题意易得∠B=30°,∠BAC=105°,∠BCA=45°,AC=30千米,
在Rt△ADC中,CD=AD=AC.cos45°=30千米,
在Rt△ABD中,AB=2AD=60千米,t==4(时).
(2)由(1)知BD=AB·cos30°=30千米,
∴BC=30+30(千米) v==(千米/时).
25.解:(1)tan31°==0.600 9,
故BE=18-12.018=5.982≈5.98(米)
tan31°=FD=,FD≈29.96(米)
故两楼间的距离至少应是29.96米.毛
- 1 -
同课章节目录
