热点20 与圆有关的证明问题(含答案)
图片预览

文档简介
热点20 与圆有关的证明问题
(时间:100分钟 总分:100分)
一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是符合题目要求的)
1.已知AB、CD是⊙O的两条直径,则四边形ADBC一定是( )
A.等腰梯形 B.正方形 C.菱形 D.矩形
2.如图1,DE是⊙O的直径,弦AB⊥ED于C,连结AE、BE、AO、BO,则图中全等三角形有( )
A.3对 B.2对 C.1对 D.0对
(1) (2) (3) (4)
3.垂径定理及推论中的四条性质:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的弧.由上述四条性质组成的命题中,假命题是( )
A.①②③④ B.①③②④
C.①④②③ D.②③①④
4.Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,给出下列三个结论:①以点C为圆心,2.3cm长为半径的圆与AB相离;②以点C为圆心,2.4cm长为半径的圆与AB相切;③以点C为圆心,2.5cm长为半径的圆与AB相交,则上述结论正确的有( )
A.0个 B.1个 C.2个 D.3个
5.在⊙O中,C是的中点,D是上的任意一点(与A、C不重合),则( )
A.AC+CB=AD+DB B.AC+CBC.AC+CB>AD+DB D.AC+CB与AD+DB的大小关系不确定
6.如图2,梯形ABCD内接于⊙O,AD∥BC,EF切⊙O于点C,则图中与∠ACB相等的角(不包括∠ACB)共有( ).
A.1个 B.2个 C.3个 D.4个
7.如图3,在△ABC中,AD是高,AE是直径,AE交BC于G,有下列四个结论:①AD2=BD·CD;②BE2=EG·AE;③AE·AD=AB·AC;④AG·EG=BG·CG.其中正确结论的有( )
A.1个 B.2个 C.3个 D.4个
8.如图4,AB是⊙O的直径,CD为弦,AE⊥CD于E,BF⊥CD于F,交⊙O于G.下面的结论:①EC=DF;②AE+BF=AB;③AE=GF;④FG·FB=EC·ED.其中正确的有( )
A.①②③ B.①③④ C.②③④ D.①②④
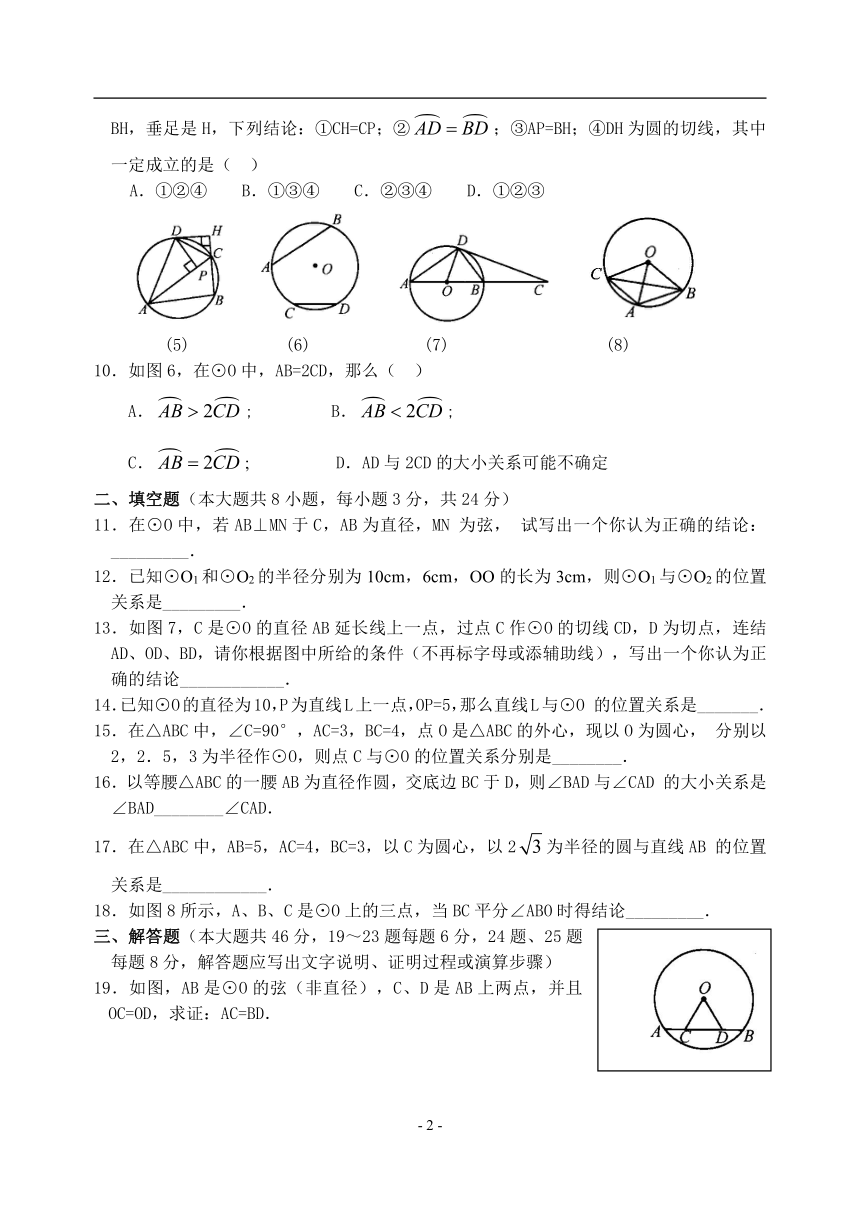
9.如图5,圆内接△ABC的外角∠ACH的平分线与圆交于D点,DP⊥AC,垂足是P,DH⊥BH,垂足是H,下列结论:①CH=CP;②;③AP=BH;④DH为圆的切线,其中一定成立的是( )
A.①②④ B.①③④ C.②③④ D.①②③
(5) (6) (7) (8)
10.如图6,在⊙O中,AB=2CD,那么( )
A.; B.;
C.; D.AD与2CD的大小关系可能不确定
二、填空题(本大题共8小题,每小题3分,共24分)
11.在⊙O中,若AB⊥MN于C,AB为直径,MN为弦,试写出一个你认为正确的结论:_________.
12.已知⊙O1和⊙O2的半径分别为10cm,6cm,OO的长为3cm,则⊙O1与⊙O2的位置关系是_________.
13.如图7,C是⊙O的直径AB延长线上一点,过点C作⊙O的切线CD,D为切点,连结AD、OD、BD,请你根据图中所给的条件(不再标字母或添辅助线),写出一个你认为正确的结论____________.
14.已知⊙O的直径为10,P为直线L上一点,OP=5,那么直线L与⊙O的位置关系是_______.
15.在△ABC中,∠C=90°,AC=3,BC=4,点O是△ABC的外心,现以O为圆心,分别以2,2.5,3为半径作⊙O,则点C与⊙O的位置关系分别是________.
16.以等腰△ABC的一腰AB为直径作圆,交底边BC于D,则∠BAD与∠CAD的大小关系是∠BAD________∠CAD.
17.在△ABC中,AB=5,AC=4,BC=3,以C为圆心,以2为半径的圆与直线AB的位置关系是____________.
18.如图8所示,A、B、C是⊙O上的三点,当BC平分∠ABO时得结论_________.
三、解答题(本大题共46分,19~23题每题6分,24题、25题每题8分,解答题应写出文字说明、证明过程或演算步骤)
19.如图,AB是⊙O的弦(非直径),C、D是AB上两点,并且OC=OD,求证:AC=BD.
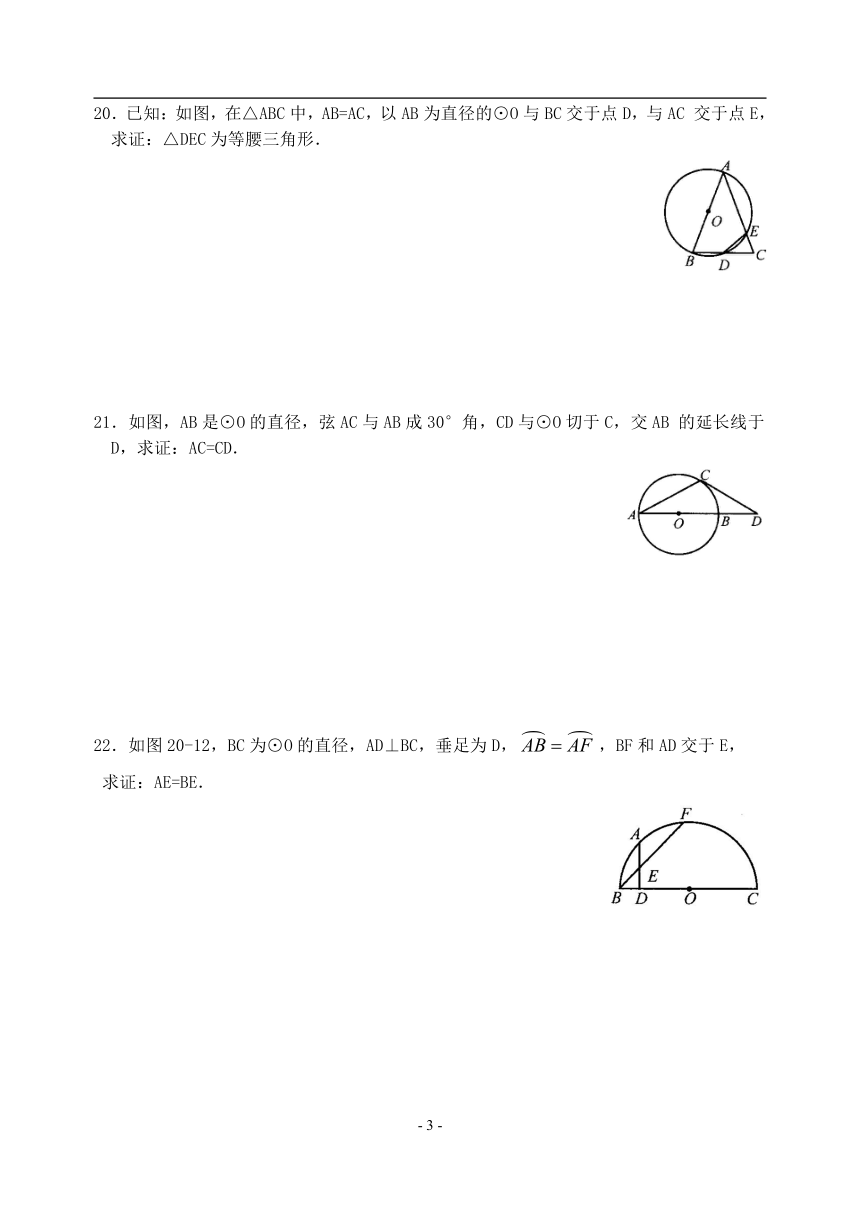
20.已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点E,求证:△DEC为等腰三角形.
21.如图,AB是⊙O的直径,弦AC与AB成30°角,CD与⊙O切于C,交AB的延长线于D,求证:AC=CD.
22.如图20-12,BC为⊙O的直径,AD⊥BC,垂足为D,,BF和AD交于E,
求证:AE=BE.
23.如图,AB是⊙O的直径,以OA为直径的⊙O1与⊙O2的弦相交于D,DE⊥OC,垂足为E.
(1)求证:AD=DC.(2)求证:DE是⊙O1的切线.
24.如图,已知直线MN与以AB为直径的半圆相切于点C,∠A=28°.
(1)求∠ACM的度数.(2)在MN上是否存在一点D,使AB·CD=AC·BC,说明理由.
25.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的半径为3.
(1)若圆心O与C重合时,⊙O与AB有怎样的位置关系?
(2)若点O沿CA移动,当OC等于多少时,⊙O与AB相切?
答案:
一、选择题
1.D 2.A 3.B 4.D 5.C 6.D 7.B 8.B 9.D 10.A
二、填空题
11.BM=BN等 12.内含 13.∠ADO=∠BDC等 14.相交或相切
15.在圆外、在圆上、在圆内 16.= 17.相交 18.OC∥AB等
三、解答题
19.证明:过点O作OE∥AB于E,则AE=BE.在△OCD中,OE⊥CD,OC=OD,
∴CE=DE.∴AC=BD.
20.证明:∵四边形ABDE是圆内接四边形,∴∠DEC=∠B.
又∵AB=AC,∴∠B=∠C,∴∠DEC=∠C,∴DE=CD.
∴△DEC为等腰三角形.
21.证明:连结BC,由AB是直径可知,
∠ABC=60°.
CD是切线∠BCD=∠A=30°∠D=30°=∠AAC=CD.
22.证明:连结AB,AC,
∠BAD=∠ABFAE=BE.
23.证明:(1)连结OD,AO是直径AD=DC.
(2)连结O1D,
DE是切线.
24.解:(1)连结BC,
∠B=62°.
MN是切线∠ACM=∠B=62°.
(2)过点B作BD⊥MN,则
△ACB∽△CNB
AB·CD1=AC·BC.
过点A作AD2⊥MN,则
△ABC∽△ACD2
CD2·AB=AC·CB
25.解:(1)过点C作CH⊥AB于H,由三角形的面积公式得AB·CH=AC·BC,
∴CH==,即圆心到直线的距离d=.
∵d=>3,∴⊙O与AB相离.
(2)过点O作OE⊥AB于E,则OE=3.
∵∠AEO=∠C=90°,∠A=∠A,∴△AOE∽△ABC,
∵OA==
∴OC=AC-OA=5-=.
∴当OC=时,⊙O与AB相切.毛
- 1 -
(时间:100分钟 总分:100分)
一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是符合题目要求的)
1.已知AB、CD是⊙O的两条直径,则四边形ADBC一定是( )
A.等腰梯形 B.正方形 C.菱形 D.矩形
2.如图1,DE是⊙O的直径,弦AB⊥ED于C,连结AE、BE、AO、BO,则图中全等三角形有( )
A.3对 B.2对 C.1对 D.0对
(1) (2) (3) (4)
3.垂径定理及推论中的四条性质:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的弧.由上述四条性质组成的命题中,假命题是( )
A.①②③④ B.①③②④
C.①④②③ D.②③①④
4.Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,给出下列三个结论:①以点C为圆心,2.3cm长为半径的圆与AB相离;②以点C为圆心,2.4cm长为半径的圆与AB相切;③以点C为圆心,2.5cm长为半径的圆与AB相交,则上述结论正确的有( )
A.0个 B.1个 C.2个 D.3个
5.在⊙O中,C是的中点,D是上的任意一点(与A、C不重合),则( )
A.AC+CB=AD+DB B.AC+CB
6.如图2,梯形ABCD内接于⊙O,AD∥BC,EF切⊙O于点C,则图中与∠ACB相等的角(不包括∠ACB)共有( ).
A.1个 B.2个 C.3个 D.4个
7.如图3,在△ABC中,AD是高,AE是直径,AE交BC于G,有下列四个结论:①AD2=BD·CD;②BE2=EG·AE;③AE·AD=AB·AC;④AG·EG=BG·CG.其中正确结论的有( )
A.1个 B.2个 C.3个 D.4个
8.如图4,AB是⊙O的直径,CD为弦,AE⊥CD于E,BF⊥CD于F,交⊙O于G.下面的结论:①EC=DF;②AE+BF=AB;③AE=GF;④FG·FB=EC·ED.其中正确的有( )
A.①②③ B.①③④ C.②③④ D.①②④
9.如图5,圆内接△ABC的外角∠ACH的平分线与圆交于D点,DP⊥AC,垂足是P,DH⊥BH,垂足是H,下列结论:①CH=CP;②;③AP=BH;④DH为圆的切线,其中一定成立的是( )
A.①②④ B.①③④ C.②③④ D.①②③
(5) (6) (7) (8)
10.如图6,在⊙O中,AB=2CD,那么( )
A.; B.;
C.; D.AD与2CD的大小关系可能不确定
二、填空题(本大题共8小题,每小题3分,共24分)
11.在⊙O中,若AB⊥MN于C,AB为直径,MN为弦,试写出一个你认为正确的结论:_________.
12.已知⊙O1和⊙O2的半径分别为10cm,6cm,OO的长为3cm,则⊙O1与⊙O2的位置关系是_________.
13.如图7,C是⊙O的直径AB延长线上一点,过点C作⊙O的切线CD,D为切点,连结AD、OD、BD,请你根据图中所给的条件(不再标字母或添辅助线),写出一个你认为正确的结论____________.
14.已知⊙O的直径为10,P为直线L上一点,OP=5,那么直线L与⊙O的位置关系是_______.
15.在△ABC中,∠C=90°,AC=3,BC=4,点O是△ABC的外心,现以O为圆心,分别以2,2.5,3为半径作⊙O,则点C与⊙O的位置关系分别是________.
16.以等腰△ABC的一腰AB为直径作圆,交底边BC于D,则∠BAD与∠CAD的大小关系是∠BAD________∠CAD.
17.在△ABC中,AB=5,AC=4,BC=3,以C为圆心,以2为半径的圆与直线AB的位置关系是____________.
18.如图8所示,A、B、C是⊙O上的三点,当BC平分∠ABO时得结论_________.
三、解答题(本大题共46分,19~23题每题6分,24题、25题每题8分,解答题应写出文字说明、证明过程或演算步骤)
19.如图,AB是⊙O的弦(非直径),C、D是AB上两点,并且OC=OD,求证:AC=BD.
20.已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点E,求证:△DEC为等腰三角形.
21.如图,AB是⊙O的直径,弦AC与AB成30°角,CD与⊙O切于C,交AB的延长线于D,求证:AC=CD.
22.如图20-12,BC为⊙O的直径,AD⊥BC,垂足为D,,BF和AD交于E,
求证:AE=BE.
23.如图,AB是⊙O的直径,以OA为直径的⊙O1与⊙O2的弦相交于D,DE⊥OC,垂足为E.
(1)求证:AD=DC.(2)求证:DE是⊙O1的切线.
24.如图,已知直线MN与以AB为直径的半圆相切于点C,∠A=28°.
(1)求∠ACM的度数.(2)在MN上是否存在一点D,使AB·CD=AC·BC,说明理由.
25.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的半径为3.
(1)若圆心O与C重合时,⊙O与AB有怎样的位置关系?
(2)若点O沿CA移动,当OC等于多少时,⊙O与AB相切?
答案:
一、选择题
1.D 2.A 3.B 4.D 5.C 6.D 7.B 8.B 9.D 10.A
二、填空题
11.BM=BN等 12.内含 13.∠ADO=∠BDC等 14.相交或相切
15.在圆外、在圆上、在圆内 16.= 17.相交 18.OC∥AB等
三、解答题
19.证明:过点O作OE∥AB于E,则AE=BE.在△OCD中,OE⊥CD,OC=OD,
∴CE=DE.∴AC=BD.
20.证明:∵四边形ABDE是圆内接四边形,∴∠DEC=∠B.
又∵AB=AC,∴∠B=∠C,∴∠DEC=∠C,∴DE=CD.
∴△DEC为等腰三角形.
21.证明:连结BC,由AB是直径可知,
∠ABC=60°.
CD是切线∠BCD=∠A=30°∠D=30°=∠AAC=CD.
22.证明:连结AB,AC,
∠BAD=∠ABFAE=BE.
23.证明:(1)连结OD,AO是直径AD=DC.
(2)连结O1D,
DE是切线.
24.解:(1)连结BC,
∠B=62°.
MN是切线∠ACM=∠B=62°.
(2)过点B作BD⊥MN,则
△ACB∽△CNB
AB·CD1=AC·BC.
过点A作AD2⊥MN,则
△ABC∽△ACD2
CD2·AB=AC·CB
25.解:(1)过点C作CH⊥AB于H,由三角形的面积公式得AB·CH=AC·BC,
∴CH==,即圆心到直线的距离d=.
∵d=>3,∴⊙O与AB相离.
(2)过点O作OE⊥AB于E,则OE=3.
∵∠AEO=∠C=90°,∠A=∠A,∴△AOE∽△ABC,
∵OA==
∴OC=AC-OA=5-=.
∴当OC=时,⊙O与AB相切.毛
- 1 -
同课章节目录
