苏科版九年级数学上册试题 第二章《对称图形—圆》单元测试卷(含答案)
文档属性
| 名称 | 苏科版九年级数学上册试题 第二章《对称图形—圆》单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 188.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 21:05:14 | ||
图片预览


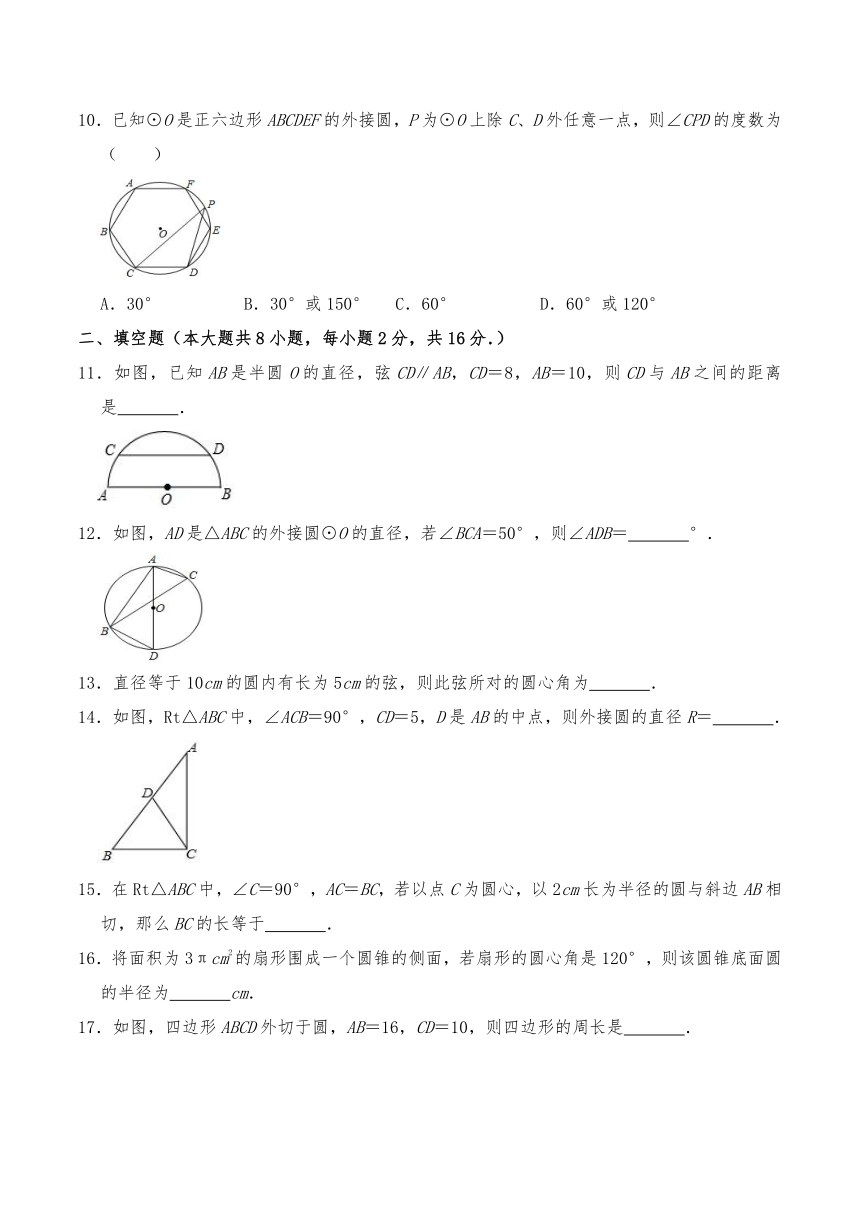

文档简介
第二章《对称图形—圆》单元测试卷
一、选择题(本大题共10小题,每小题2分,共20分).
1.如图,AB是⊙O的直径,点C、D在⊙O上,∠BDC=20°,则∠AOC的大小为( )
A.40° B.140° C.160° D.170°
2.如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于( )
A.10° B.14° C.16° D.26°
3.一个圆锥的底面半径是4cm,其侧面展开图的圆心角是120°,则圆锥的母线长是( )
A.8cm B.12cm C.16cm D.24cm
4.如图,在⊙O中,AB为直径,C,E在圆周上,若∠COB=100°,则∠AEC的度数为( )
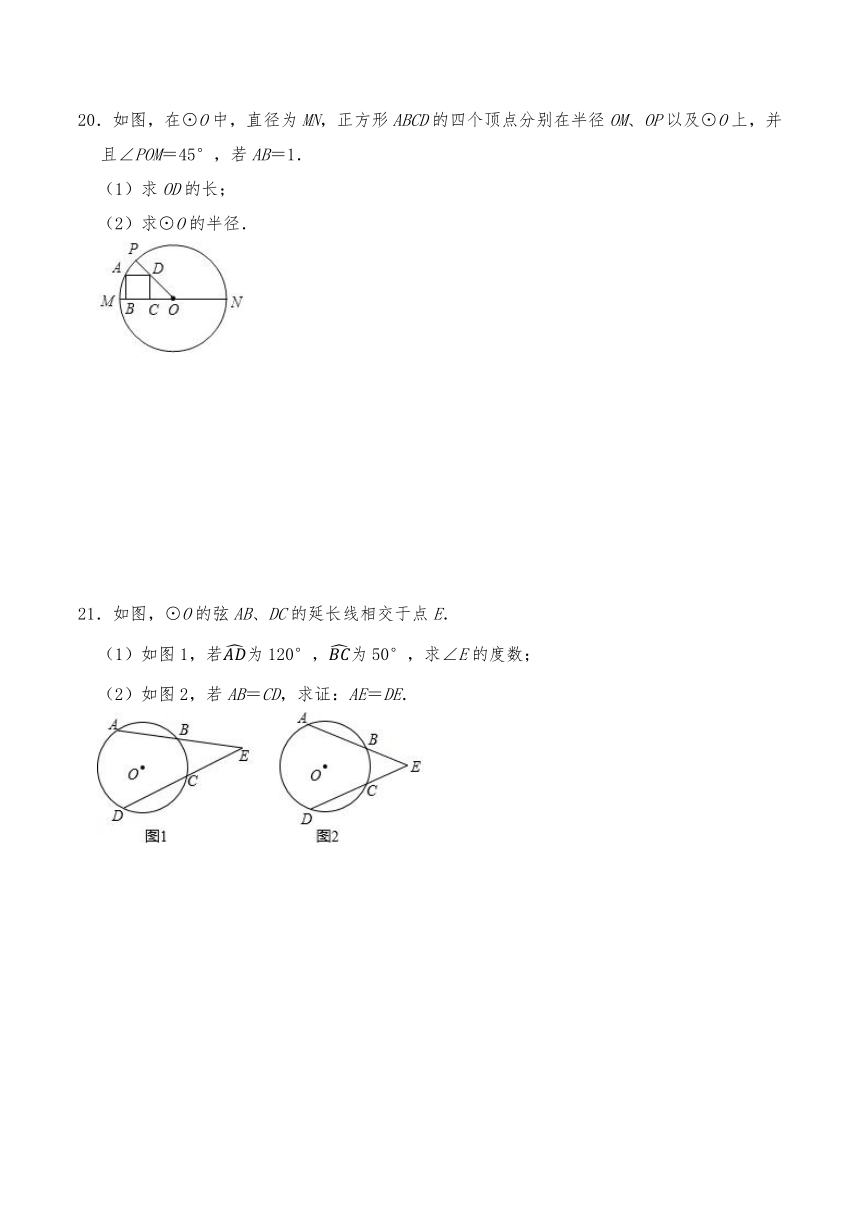
A.30° B.20° C.40° D.50°
5.如图,AB是⊙O的直径,C,D为⊙O上的点,弧AD=弧CD,若∠DAC=25°,则∠CAB的度数为( )
A.30° B.40° C.50° D.60°
6.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( )
A.100° B.110° C.120° D.130°
7.如图是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面半径是( )
A.3.6 B.1.8 C.3 D.6
8.有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是( )
A.淇淇说的对,且∠A的另一个值是115°
B.淇淇说的不对,∠A就得65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同值
9.⊙O是△ABC的外接圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
10.已知⊙O是正六边形ABCDEF的外接圆,P为⊙O上除C、D外任意一点,则∠CPD的度数为( )
A.30° B.30°或150° C.60° D.60°或120°
二、填空题(本大题共8小题,每小题2分,共16分.)
11.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 .
12.如图,AD是△ABC的外接圆⊙O的直径,若∠BCA=50°,则∠ADB= °.
13.直径等于10cm的圆内有长为5cm的弦,则此弦所对的圆心角为 .
14.如图,Rt△ABC中,∠ACB=90°,CD=5,D是AB的中点,则外接圆的直径R= .
15.在Rt△ABC中,∠C=90°,AC=BC,若以点C为圆心,以2cm长为半径的圆与斜边AB相切,那么BC的长等于 .
16.将面积为3πcm2的扇形围成一个圆锥的侧面,若扇形的圆心角是120°,则该圆锥底面圆的半径为 cm.
17.如图,四边形ABCD外切于圆,AB=16,CD=10,则四边形的周长是 .
18.如图是一块直角三角形木料,∠A=90°,AB=3,AC=4,木工师傅要从中裁下一块圆形用料,则可裁圆形木料的最大半径为 .
三、解答题(本大题共8小题,共64分.)
19.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.
20.如图,在⊙O中,直径为MN,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,并且∠POM=45°,若AB=1.
(1)求OD的长;
(2)求⊙O的半径.
21.如图,⊙O的弦AB、DC的延长线相交于点E.
(1)如图1,若为120°,为50°,求∠E的度数;
(2)如图2,若AB=CD,求证:AE=DE.
22.在△ABC中,∠C=90°,AC=6,BC=8,求这个三角形外接圆的半径和面积.
23.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC交⊙O于点E,点E不与点A重合,
(1)AB与AC的大小有什么关系?为什么?
(2)若∠B=60°,BD=3,求AB的长.
24.如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)若∠CBD=30°,BC=3,求⊙O半径.
25.如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.
(1)求证:AE=AB;
(2)若AB=10,BC=6,求CD的长.
26.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=6,∠CBD=30°,求图中阴影部分的面积.
答案
一、选择题
B.C.B.C.B.C.A.A.A.B.
二、填空题
11.3.
12.50.
13.60°.
14.10.
15.2cm.
16.1.
17.52.
18.1.
三、解答题
19.过O点作半径OD⊥AB于E,如图,
∴AE=BEAB8=4,
在Rt△AEO中,OE3,
∴ED=OD﹣OE=5﹣3=2,
答:筒车工作时,盛水桶在水面以下的最大深度为2m.
20.(1)如图,
∵四边形ABCD 为正方形,
∴DC=BC=AB=1,∠DCO=∠ABC=90°,
∵∠DCO=45°,
∴CO=DC=1,
∴ODCO;
(2)BO=BC+CO=BC+CD1+1=2,.
连接AO,
则△ABO 为直角三角形,
于是 AO.
即⊙O的半径为.
21.(1)解:连接AC.
∵弧AD为120°,弧BC为50°,
∴∠ACD=60°,∠BAC=25°,
∵∠ACD=∠BAC+∠E
∴∠E=∠ACD﹣∠BAC=60°﹣25°=35°;
(2)证明:连接AD.
∵AB=CD,
∴弧AB=弧CD,
∴弧AC=弧BD,
∴∠ADC=∠DAB,
∴AE=DE.
22.∵∠C=90°,AC=6,BC=8,
∴AB10,
∴Rt△ABC的外接圆的半径为5,
面积为π×52=25π.
23.(1)AB=AC.理由如下:
连接AD,如图,
∵AB是⊙O的直径,
∴AD⊥BC,
∵BD=CD,
∴AB=AC;
(2)在Rt△ABD中,∵∠B=60°,
∴AB=2BD=2×3=6.
24.(1)证明:如图,连接OD,
∵OD=OB=OA,
∴∠OBD=∠ODB,∠ODA=∠OAD,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB.
∵AB为⊙O的直径,
∴∠ADB=∠ODB+∠ODA=90°,
∴∠CDA+∠ODA=∠ODC=90°.
∴OD⊥CD,
∴CD是⊙O的切线;
(2)∵∠CBD=30°,∠OBD=∠ODB,
∴∠AOD=∠OBD+∠ODB=60°,
∴∠C=30°.
∵∠ODC=90°.
∴OD=OBOC,
∴OBBC,
∵BC=3,
∴OB=1,
∴⊙O半径为1.
25.(1)证明:连接AC、OC,如图,
∵CD为切线,
∴OC⊥CD,
∵CD⊥AD,
∴OC∥AD,
∴∠OCB=∠E,
∵OB=OC,
∴∠OCB=∠B,
∴∠B=∠E,
∴AE=AB;
(2)解:∵AB为直径,
∴∠ACB=90°,
∴AC8,
∵AB=AE=10,AC⊥BE,
∴CE=BC=6,
∵CD AEAC CE,
∴CD.
26.(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,即OC⊥AD,
又∵OC为半径,
∴AE=ED,
(2)解:连接CD,OD,
∵OC∥BD,
∴∠OCB=∠CBD=30°,
∵OC=OB,
∴∠OCB=∠OBC=30°,
∴∠AOC=∠OCB+∠OBC=60°,
∵∠COD=2∠CBD=60°,
∴∠AOD=120°,
∵AB=6,
∴BD=3,AD=3,
∵OA=OB,AE=ED,
∴,
∴S阴影=S扇形AOD﹣S△AOD3π.
一、选择题(本大题共10小题,每小题2分,共20分).
1.如图,AB是⊙O的直径,点C、D在⊙O上,∠BDC=20°,则∠AOC的大小为( )
A.40° B.140° C.160° D.170°
2.如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于( )
A.10° B.14° C.16° D.26°
3.一个圆锥的底面半径是4cm,其侧面展开图的圆心角是120°,则圆锥的母线长是( )
A.8cm B.12cm C.16cm D.24cm
4.如图,在⊙O中,AB为直径,C,E在圆周上,若∠COB=100°,则∠AEC的度数为( )
A.30° B.20° C.40° D.50°
5.如图,AB是⊙O的直径,C,D为⊙O上的点,弧AD=弧CD,若∠DAC=25°,则∠CAB的度数为( )
A.30° B.40° C.50° D.60°
6.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( )
A.100° B.110° C.120° D.130°
7.如图是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面半径是( )
A.3.6 B.1.8 C.3 D.6
8.有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是( )
A.淇淇说的对,且∠A的另一个值是115°
B.淇淇说的不对,∠A就得65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同值
9.⊙O是△ABC的外接圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
10.已知⊙O是正六边形ABCDEF的外接圆,P为⊙O上除C、D外任意一点,则∠CPD的度数为( )
A.30° B.30°或150° C.60° D.60°或120°
二、填空题(本大题共8小题,每小题2分,共16分.)
11.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 .
12.如图,AD是△ABC的外接圆⊙O的直径,若∠BCA=50°,则∠ADB= °.
13.直径等于10cm的圆内有长为5cm的弦,则此弦所对的圆心角为 .
14.如图,Rt△ABC中,∠ACB=90°,CD=5,D是AB的中点,则外接圆的直径R= .
15.在Rt△ABC中,∠C=90°,AC=BC,若以点C为圆心,以2cm长为半径的圆与斜边AB相切,那么BC的长等于 .
16.将面积为3πcm2的扇形围成一个圆锥的侧面,若扇形的圆心角是120°,则该圆锥底面圆的半径为 cm.
17.如图,四边形ABCD外切于圆,AB=16,CD=10,则四边形的周长是 .
18.如图是一块直角三角形木料,∠A=90°,AB=3,AC=4,木工师傅要从中裁下一块圆形用料,则可裁圆形木料的最大半径为 .
三、解答题(本大题共8小题,共64分.)
19.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.
20.如图,在⊙O中,直径为MN,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,并且∠POM=45°,若AB=1.
(1)求OD的长;
(2)求⊙O的半径.
21.如图,⊙O的弦AB、DC的延长线相交于点E.
(1)如图1,若为120°,为50°,求∠E的度数;
(2)如图2,若AB=CD,求证:AE=DE.
22.在△ABC中,∠C=90°,AC=6,BC=8,求这个三角形外接圆的半径和面积.
23.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC交⊙O于点E,点E不与点A重合,
(1)AB与AC的大小有什么关系?为什么?
(2)若∠B=60°,BD=3,求AB的长.
24.如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)若∠CBD=30°,BC=3,求⊙O半径.
25.如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.
(1)求证:AE=AB;
(2)若AB=10,BC=6,求CD的长.
26.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=6,∠CBD=30°,求图中阴影部分的面积.
答案
一、选择题
B.C.B.C.B.C.A.A.A.B.
二、填空题
11.3.
12.50.
13.60°.
14.10.
15.2cm.
16.1.
17.52.
18.1.
三、解答题
19.过O点作半径OD⊥AB于E,如图,
∴AE=BEAB8=4,
在Rt△AEO中,OE3,
∴ED=OD﹣OE=5﹣3=2,
答:筒车工作时,盛水桶在水面以下的最大深度为2m.
20.(1)如图,
∵四边形ABCD 为正方形,
∴DC=BC=AB=1,∠DCO=∠ABC=90°,
∵∠DCO=45°,
∴CO=DC=1,
∴ODCO;
(2)BO=BC+CO=BC+CD1+1=2,.
连接AO,
则△ABO 为直角三角形,
于是 AO.
即⊙O的半径为.
21.(1)解:连接AC.
∵弧AD为120°,弧BC为50°,
∴∠ACD=60°,∠BAC=25°,
∵∠ACD=∠BAC+∠E
∴∠E=∠ACD﹣∠BAC=60°﹣25°=35°;
(2)证明:连接AD.
∵AB=CD,
∴弧AB=弧CD,
∴弧AC=弧BD,
∴∠ADC=∠DAB,
∴AE=DE.
22.∵∠C=90°,AC=6,BC=8,
∴AB10,
∴Rt△ABC的外接圆的半径为5,
面积为π×52=25π.
23.(1)AB=AC.理由如下:
连接AD,如图,
∵AB是⊙O的直径,
∴AD⊥BC,
∵BD=CD,
∴AB=AC;
(2)在Rt△ABD中,∵∠B=60°,
∴AB=2BD=2×3=6.
24.(1)证明:如图,连接OD,
∵OD=OB=OA,
∴∠OBD=∠ODB,∠ODA=∠OAD,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB.
∵AB为⊙O的直径,
∴∠ADB=∠ODB+∠ODA=90°,
∴∠CDA+∠ODA=∠ODC=90°.
∴OD⊥CD,
∴CD是⊙O的切线;
(2)∵∠CBD=30°,∠OBD=∠ODB,
∴∠AOD=∠OBD+∠ODB=60°,
∴∠C=30°.
∵∠ODC=90°.
∴OD=OBOC,
∴OBBC,
∵BC=3,
∴OB=1,
∴⊙O半径为1.
25.(1)证明:连接AC、OC,如图,
∵CD为切线,
∴OC⊥CD,
∵CD⊥AD,
∴OC∥AD,
∴∠OCB=∠E,
∵OB=OC,
∴∠OCB=∠B,
∴∠B=∠E,
∴AE=AB;
(2)解:∵AB为直径,
∴∠ACB=90°,
∴AC8,
∵AB=AE=10,AC⊥BE,
∴CE=BC=6,
∵CD AEAC CE,
∴CD.
26.(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,即OC⊥AD,
又∵OC为半径,
∴AE=ED,
(2)解:连接CD,OD,
∵OC∥BD,
∴∠OCB=∠CBD=30°,
∵OC=OB,
∴∠OCB=∠OBC=30°,
∴∠AOC=∠OCB+∠OBC=60°,
∵∠COD=2∠CBD=60°,
∴∠AOD=120°,
∵AB=6,
∴BD=3,AD=3,
∵OA=OB,AE=ED,
∴,
∴S阴影=S扇形AOD﹣S△AOD3π.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
