八年级数学下册试题 9.4矩形、菱形、正方形同步练习-苏科版(含答案)
文档属性
| 名称 | 八年级数学下册试题 9.4矩形、菱形、正方形同步练习-苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 176.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 21:36:08 | ||
图片预览



文档简介
9.4矩形、菱形、正方形
一.选择题
1.下列判定正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是菱形
C.四条边相等的四边形是正方形
D.对角线互相平分且相等的四边形是矩形
2.如图,在菱形ABCD中,对角线AC、BD交于点O,且AC=6,BD=8,过A点作AE垂直BC,交BC于点E,则的值为( )
A. B. C. D.
3.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为4.8km,则M,C两点间的距离为( )
A.1.2km B.2.4km C.3.6km D.4.8km
4.如图,在矩形ABCD中,两条对角线AC与BD相交于点O,AB=3,OA=2,则AD的长为( )
A.5 B. C. D.
5.如图,矩形ABCD的对角线AC、BD相交于点O,∠ABO=60°,若矩形的对角线长为6.则线段AD的长是( )
A.3 B.4 C.2 D.3
6.平行四边形、矩形、菱形、正方形共有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.对角线互相垂直平分
7.如图,长方形ABCD中,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为( )
A.2或8 B.或18 C.或2 D.2或18
8.如图,矩形ABCD的对角线AC,BD相交于点O,且∠AOD=120°.过点A作AE⊥BD于点E,则BE:ED等于( )
A.1:3 B.1:4 C.2:3 D.2:5
9.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
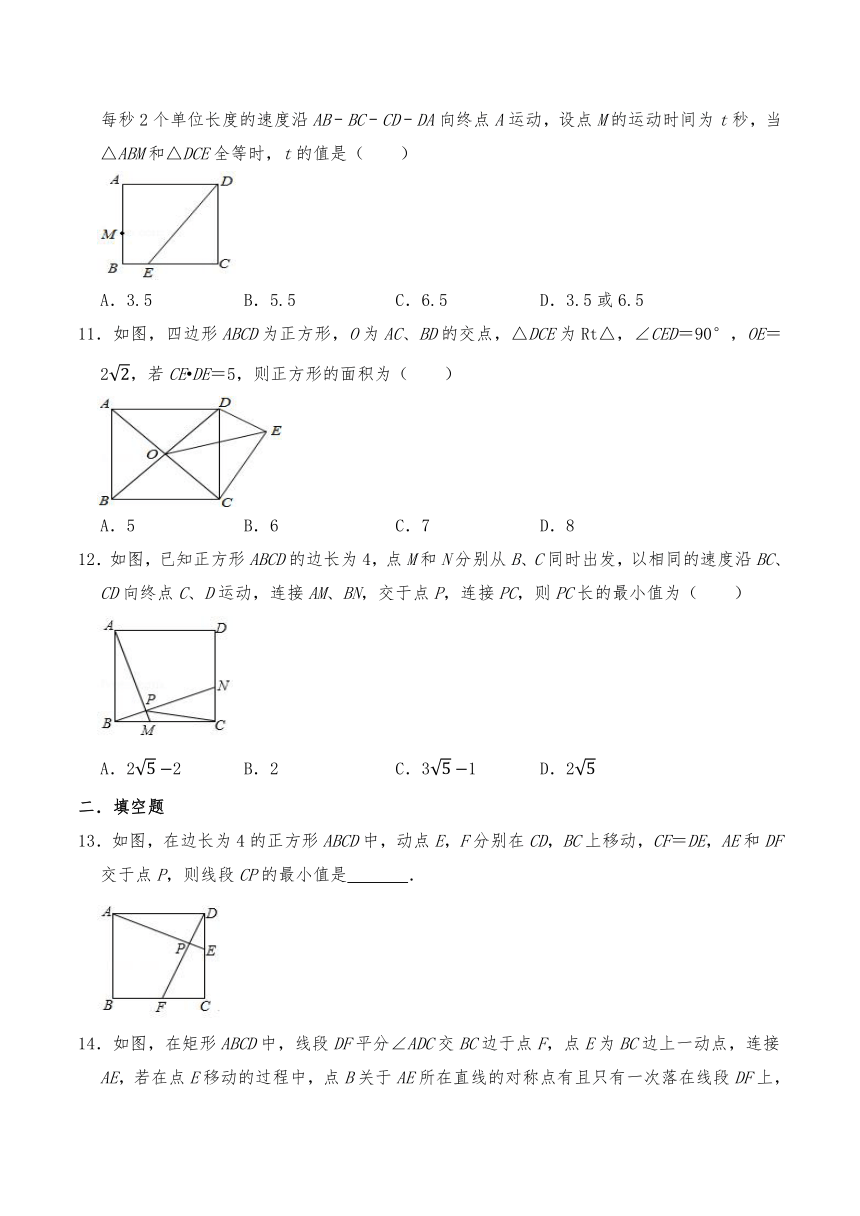
10.如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( )
A.3.5 B.5.5 C.6.5 D.3.5或6.5
11.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE DE=5,则正方形的面积为( )
A.5 B.6 C.7 D.8
12.如图,已知正方形ABCD的边长为4,点M和N分别从B、C同时出发,以相同的速度沿BC、CD向终点C、D运动,连接AM、BN,交于点P,连接PC,则PC长的最小值为( )
A.22 B.2 C.31 D.2
二.填空题
13.如图,在边长为4的正方形ABCD中,动点E,F分别在CD,BC上移动,CF=DE,AE和DF交于点P,则线段CP的最小值是 .
14.如图,在矩形ABCD中,线段DF平分∠ADC交BC边于点F,点E为BC边上一动点,连接AE,若在点E移动的过程中,点B关于AE所在直线的对称点有且只有一次落在线段DF上,则BC:AB= .
15.如图,菱形ABCD的边长AB=3,对角线BD=4,点E,F在BD上,且BE=DF,连接AE,AF,CE,CF.则四边形AECF的周长为 .
16.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为 .
17.如图,四边形ABCD是长方形,F是DA延长线上一点,CF交AB于点E,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F.若∠ECB=20°,则∠ACD的度数是 .
18.在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,与此同时点Q从点C出发,以acm/秒的速度沿CD向点D运动,当点P到达C点或点Q到达D点时,P、Q运动停止,当a= 2或2.4 时,△ABP与△PQC全等.
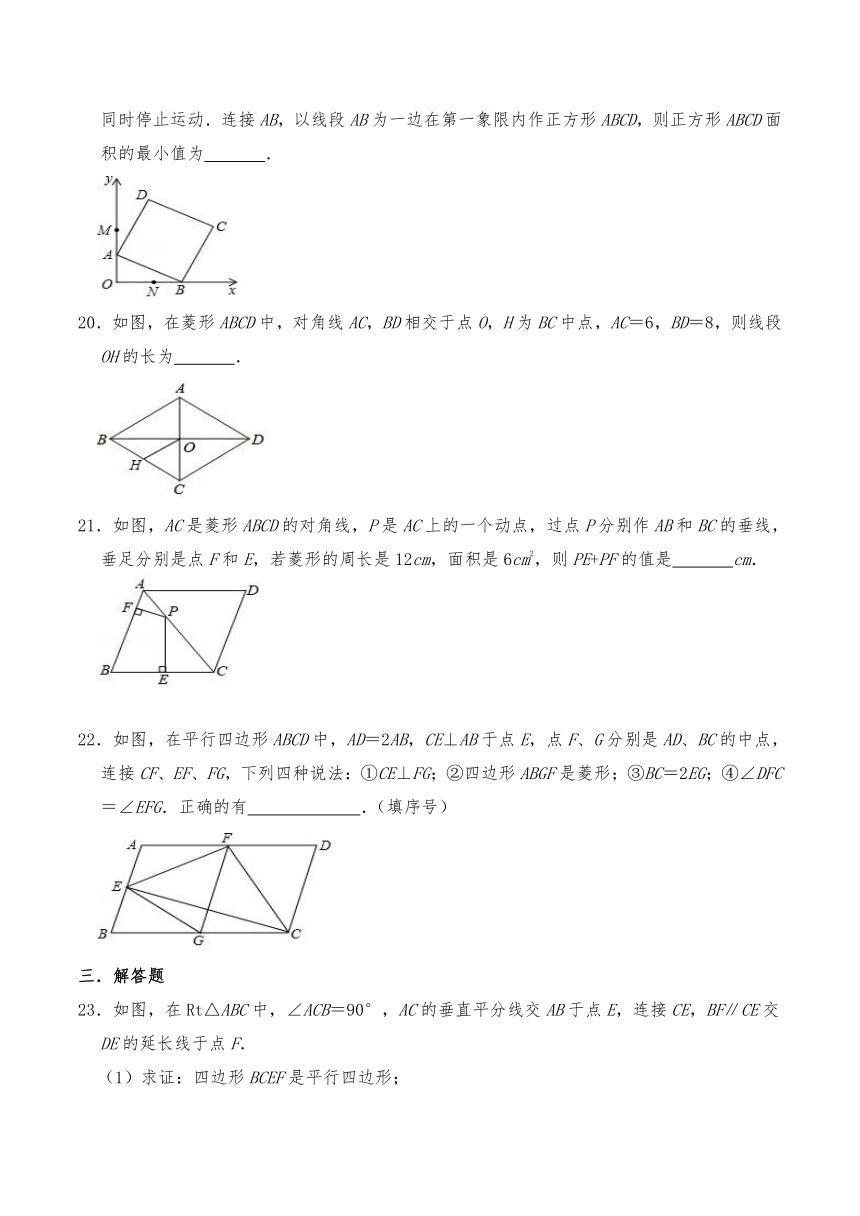
19.如图,在平面直角坐标系中,点A从点M(0,5)出发向原点O匀速运动,与此同时点B从点N(3,0)出发,在x轴正半轴上以相同的速度向右运动,当点A到达终点O时,两点同时停止运动.连接AB,以线段AB为一边在第一象限内作正方形ABCD,则正方形ABCD面积的最小值为 .
20.如图,在菱形ABCD中,对角线AC,BD相交于点O,H为BC中点,AC=6,BD=8,则线段OH的长为 .
21.如图,AC是菱形ABCD的对角线,P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2,则PE+PF的值是 cm.
22.如图,在平行四边形ABCD中,AD=2AB,CE⊥AB于点E,点F、G分别是AD、BC的中点,连接CF、EF、FG,下列四种说法:①CE⊥FG;②四边形ABGF是菱形;③BC=2EG;④∠DFC=∠EFG.正确的有 .(填序号)
三.解答题
23.如图,在Rt△ABC中,∠ACB=90°,AC的垂直平分线交AB于点E,连接CE,BF∥CE交DE的延长线于点F.
(1)求证:四边形BCEF是平行四边形;
(2)当∠A满足什么条件时,四边形BCEF是菱形?回答并证明你的结论.
24.如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,DC=BF,点E是CF的中点.
(1)求证:DE⊥CF;
(2)求证:∠B=2∠BCF.
25.如图,BD是△ABC的角平分线,过点作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)若∠ABC=60°,∠ACB=45°,CD=6,求菱形BEDF的边长.
26.已知:在矩形ABCD中,点E在BC边上,连接DE,且DE=BC,过点A作AF⊥DE于点F.
(1)如图1,求证:AB=AF;
(2)如图2,连接AE,当BE=DF时,在不添加任何辅助线的情况下,请直接写出图2中所有长度等于AB的线段.
27.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:CE=DE.
(2)当BE=2,CE=1时,求菱形的边长.
28.如图,在平行四边形ABCD中,点O是BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠ADE= °时,四边形BECD是菱形.
29.如图,已知四边形ABCD中,∠ABC=∠ADC=90°,点E是AC中点,点F是BD中点.
(1)求证:EF⊥BD;
(2)过点D作DH⊥AC于H点,如果BD平分∠HDE,求证:BA=BC.
30.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OD的长.
答案
一.选择题
D.C.B.D.A.A.D.A.A.D.B.A.
二.填空题
13.22.
14.:1.
15.4.
16.10.
17.30°.
18.2或2.4.
19.32.
20.2.5.
21.2.
22.①②③④.
三.解答题
23.解:(1)证明:∵DF垂直平分AC,∠ACB=90°,
∴DF∥BC,
又∵BF∥CE,
∴四边形BCEF是平行四边形;
(2)当∠A=30°时,四边形BCEF是菱形.
理由是:
∵DF垂直平分AC,∠ACB=90°,∠A=30°,
∴EA=EC,∠ABC=90°﹣30°=60°,
∴∠ACE=∠A=30°,
即∠BCE=90°﹣30°=60°,
∴△BCE是等边三角形,
∴BC=EC,
由(1)得四边形BCEF是平行四边形,
∴四边形BCEF是菱形.
24.证明:(1)连接DF,
∵AD是边BC上的高,
∴∠ADB=90°,
∵点F是AB的中点,
∴DFAB=BF,
∵DC=BF,
∴DC=DF,
∵点E是CF的中点.
∴DE⊥CF;
(2)∵DC=DF,
∴∠DFC=∠DCF,
∴∠FDB=∠DFC+∠DCF=2∠DFC,
∵DF=BF,
∴∠FDB=∠B,
∴∠B=2∠BCF.
25.证明:(1)∵DE∥BC,DF∥AB,
∴四边形DEBF是平行四边形,
∵DE∥BC,
∴∠EDB=∠DBF,
∵BD平分∠ABC,
∴∠ABD=∠DBF∠ABC,
∴∠ABD=∠EDB,
∴DE=BE,
又∵四边形BEDF为平行四边形,
∴四边形BEDF是菱形;
(2)如图,过点D作DH⊥BC于H,
∵DF∥AB,
∴∠ABC=∠DFC=60°,
∵DH⊥BC,
∴∠FDH=30°,
∴FHDF,DHFHDF,
∵∠C=45°,DH⊥BC,
∴∠C=∠HDC=45°,
∴DCDHDF=6,
∴DF=2,
∴菱形BEDF的边长为2.
26.证明:(1)∵四边形ABCD是矩形,AF⊥DE,
∴AD∥BC,AD=BC,AB=CD,∠C=∠AFD=90°,
∴∠ADE=∠DEC,
∵DE=BC,
∴AD=DE,
在△ADF和△DEC中,
,
∴△ADF≌△DEC(AAS),
∴AF=CD,
∴AF=AB;
(2)AD,BC,DE的长度等于AB,
理由如下:∵△ADF≌△DEC,
∴CE=DF,
∴BE=EF,
∵BE=DF,
∴BE=EC=DF=EF,
∴DE=2EC,
∵DE2=EC2+CD2,
∴DEAB,
∴AD=BC=DEAB.
27.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
∵AE=DE,
∴CE=DE;
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AH⊥BD,BH=DH,AH=CH,
∵CE=DE=AE=1,
∴BD=BE+DE=2+1=3,
∴BHBD,EH=BE﹣BH=2,
在Rt△AHE中,由勾股定理得:AH,
在Rt△AHB中,由勾股定理得:AB,
∴菱形的边长为.
28.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,
,
∴△BOE≌△COD(AAS);
∴OE=OD,
∴四边形BECD是平行四边形;
(2)解:当∠ADE=90°时,四边形BECD是菱形,理由如下:
∵∠A=50°,∠ADE=90°,
∴∠AED=40°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CBE=∠A=50°,
∴∠BOE=90°,
∴BC⊥DE,
∴四边形BECD是菱形,
故答案为:90.
29.(1)证明:∵∠ABC=∠ADC=90°,点E是AC中点,
∴DEAC,BEAC,
∴DE=BE,
∵点F是BD中点,
∴EF⊥BD;
(2)证明:设AC,BD交于点O,
∵DH⊥AC,EF⊥BD,
∴∠DHO=∠EFO=90°,
∵∠DOH=∠BOE,
∴∠HDF=∠OEF,
∵DE=BE,
∴∠EDO=∠EBO,
∵BD平分∠HDE,
∴∠HDF=∠BDE,
∴∠OEF=∠OBE,
∵∠OEF+∠EOF=90°,
∴∠EOF+∠EBO=90°,
∴∠BEO=90°,
∴BE⊥AC,
∴BA=BC.
30.(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)∵四边形ABEF是正方形,
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∵AD=AE,
∴AD﹣AF=AE﹣AG,
即DF=EG,
在△DFO和△EGO中,,
∴△DFO≌△EGO(AAS),
∴FO=GO,FD=EG
∵∠DAE=∠AEF=45°,∠AFE=∠AGD=90°,
∴DF=FO=OG=EG,
∴DOOFOG,
∴DG=DO+OGOG+OG=1,
∴OG1,
∴OD(1)=2.
一.选择题
1.下列判定正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是菱形
C.四条边相等的四边形是正方形
D.对角线互相平分且相等的四边形是矩形
2.如图,在菱形ABCD中,对角线AC、BD交于点O,且AC=6,BD=8,过A点作AE垂直BC,交BC于点E,则的值为( )
A. B. C. D.
3.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为4.8km,则M,C两点间的距离为( )
A.1.2km B.2.4km C.3.6km D.4.8km
4.如图,在矩形ABCD中,两条对角线AC与BD相交于点O,AB=3,OA=2,则AD的长为( )
A.5 B. C. D.
5.如图,矩形ABCD的对角线AC、BD相交于点O,∠ABO=60°,若矩形的对角线长为6.则线段AD的长是( )
A.3 B.4 C.2 D.3
6.平行四边形、矩形、菱形、正方形共有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.对角线互相垂直平分
7.如图,长方形ABCD中,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为( )
A.2或8 B.或18 C.或2 D.2或18
8.如图,矩形ABCD的对角线AC,BD相交于点O,且∠AOD=120°.过点A作AE⊥BD于点E,则BE:ED等于( )
A.1:3 B.1:4 C.2:3 D.2:5
9.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
10.如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( )
A.3.5 B.5.5 C.6.5 D.3.5或6.5
11.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE DE=5,则正方形的面积为( )
A.5 B.6 C.7 D.8
12.如图,已知正方形ABCD的边长为4,点M和N分别从B、C同时出发,以相同的速度沿BC、CD向终点C、D运动,连接AM、BN,交于点P,连接PC,则PC长的最小值为( )
A.22 B.2 C.31 D.2
二.填空题
13.如图,在边长为4的正方形ABCD中,动点E,F分别在CD,BC上移动,CF=DE,AE和DF交于点P,则线段CP的最小值是 .
14.如图,在矩形ABCD中,线段DF平分∠ADC交BC边于点F,点E为BC边上一动点,连接AE,若在点E移动的过程中,点B关于AE所在直线的对称点有且只有一次落在线段DF上,则BC:AB= .
15.如图,菱形ABCD的边长AB=3,对角线BD=4,点E,F在BD上,且BE=DF,连接AE,AF,CE,CF.则四边形AECF的周长为 .
16.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为 .
17.如图,四边形ABCD是长方形,F是DA延长线上一点,CF交AB于点E,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F.若∠ECB=20°,则∠ACD的度数是 .
18.在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,与此同时点Q从点C出发,以acm/秒的速度沿CD向点D运动,当点P到达C点或点Q到达D点时,P、Q运动停止,当a= 2或2.4 时,△ABP与△PQC全等.
19.如图,在平面直角坐标系中,点A从点M(0,5)出发向原点O匀速运动,与此同时点B从点N(3,0)出发,在x轴正半轴上以相同的速度向右运动,当点A到达终点O时,两点同时停止运动.连接AB,以线段AB为一边在第一象限内作正方形ABCD,则正方形ABCD面积的最小值为 .
20.如图,在菱形ABCD中,对角线AC,BD相交于点O,H为BC中点,AC=6,BD=8,则线段OH的长为 .
21.如图,AC是菱形ABCD的对角线,P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2,则PE+PF的值是 cm.
22.如图,在平行四边形ABCD中,AD=2AB,CE⊥AB于点E,点F、G分别是AD、BC的中点,连接CF、EF、FG,下列四种说法:①CE⊥FG;②四边形ABGF是菱形;③BC=2EG;④∠DFC=∠EFG.正确的有 .(填序号)
三.解答题
23.如图,在Rt△ABC中,∠ACB=90°,AC的垂直平分线交AB于点E,连接CE,BF∥CE交DE的延长线于点F.
(1)求证:四边形BCEF是平行四边形;
(2)当∠A满足什么条件时,四边形BCEF是菱形?回答并证明你的结论.
24.如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,DC=BF,点E是CF的中点.
(1)求证:DE⊥CF;
(2)求证:∠B=2∠BCF.
25.如图,BD是△ABC的角平分线,过点作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)若∠ABC=60°,∠ACB=45°,CD=6,求菱形BEDF的边长.
26.已知:在矩形ABCD中,点E在BC边上,连接DE,且DE=BC,过点A作AF⊥DE于点F.
(1)如图1,求证:AB=AF;
(2)如图2,连接AE,当BE=DF时,在不添加任何辅助线的情况下,请直接写出图2中所有长度等于AB的线段.
27.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:CE=DE.
(2)当BE=2,CE=1时,求菱形的边长.
28.如图,在平行四边形ABCD中,点O是BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠ADE= °时,四边形BECD是菱形.
29.如图,已知四边形ABCD中,∠ABC=∠ADC=90°,点E是AC中点,点F是BD中点.
(1)求证:EF⊥BD;
(2)过点D作DH⊥AC于H点,如果BD平分∠HDE,求证:BA=BC.
30.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OD的长.
答案
一.选择题
D.C.B.D.A.A.D.A.A.D.B.A.
二.填空题
13.22.
14.:1.
15.4.
16.10.
17.30°.
18.2或2.4.
19.32.
20.2.5.
21.2.
22.①②③④.
三.解答题
23.解:(1)证明:∵DF垂直平分AC,∠ACB=90°,
∴DF∥BC,
又∵BF∥CE,
∴四边形BCEF是平行四边形;
(2)当∠A=30°时,四边形BCEF是菱形.
理由是:
∵DF垂直平分AC,∠ACB=90°,∠A=30°,
∴EA=EC,∠ABC=90°﹣30°=60°,
∴∠ACE=∠A=30°,
即∠BCE=90°﹣30°=60°,
∴△BCE是等边三角形,
∴BC=EC,
由(1)得四边形BCEF是平行四边形,
∴四边形BCEF是菱形.
24.证明:(1)连接DF,
∵AD是边BC上的高,
∴∠ADB=90°,
∵点F是AB的中点,
∴DFAB=BF,
∵DC=BF,
∴DC=DF,
∵点E是CF的中点.
∴DE⊥CF;
(2)∵DC=DF,
∴∠DFC=∠DCF,
∴∠FDB=∠DFC+∠DCF=2∠DFC,
∵DF=BF,
∴∠FDB=∠B,
∴∠B=2∠BCF.
25.证明:(1)∵DE∥BC,DF∥AB,
∴四边形DEBF是平行四边形,
∵DE∥BC,
∴∠EDB=∠DBF,
∵BD平分∠ABC,
∴∠ABD=∠DBF∠ABC,
∴∠ABD=∠EDB,
∴DE=BE,
又∵四边形BEDF为平行四边形,
∴四边形BEDF是菱形;
(2)如图,过点D作DH⊥BC于H,
∵DF∥AB,
∴∠ABC=∠DFC=60°,
∵DH⊥BC,
∴∠FDH=30°,
∴FHDF,DHFHDF,
∵∠C=45°,DH⊥BC,
∴∠C=∠HDC=45°,
∴DCDHDF=6,
∴DF=2,
∴菱形BEDF的边长为2.
26.证明:(1)∵四边形ABCD是矩形,AF⊥DE,
∴AD∥BC,AD=BC,AB=CD,∠C=∠AFD=90°,
∴∠ADE=∠DEC,
∵DE=BC,
∴AD=DE,
在△ADF和△DEC中,
,
∴△ADF≌△DEC(AAS),
∴AF=CD,
∴AF=AB;
(2)AD,BC,DE的长度等于AB,
理由如下:∵△ADF≌△DEC,
∴CE=DF,
∴BE=EF,
∵BE=DF,
∴BE=EC=DF=EF,
∴DE=2EC,
∵DE2=EC2+CD2,
∴DEAB,
∴AD=BC=DEAB.
27.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
∵AE=DE,
∴CE=DE;
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AH⊥BD,BH=DH,AH=CH,
∵CE=DE=AE=1,
∴BD=BE+DE=2+1=3,
∴BHBD,EH=BE﹣BH=2,
在Rt△AHE中,由勾股定理得:AH,
在Rt△AHB中,由勾股定理得:AB,
∴菱形的边长为.
28.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,
,
∴△BOE≌△COD(AAS);
∴OE=OD,
∴四边形BECD是平行四边形;
(2)解:当∠ADE=90°时,四边形BECD是菱形,理由如下:
∵∠A=50°,∠ADE=90°,
∴∠AED=40°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CBE=∠A=50°,
∴∠BOE=90°,
∴BC⊥DE,
∴四边形BECD是菱形,
故答案为:90.
29.(1)证明:∵∠ABC=∠ADC=90°,点E是AC中点,
∴DEAC,BEAC,
∴DE=BE,
∵点F是BD中点,
∴EF⊥BD;
(2)证明:设AC,BD交于点O,
∵DH⊥AC,EF⊥BD,
∴∠DHO=∠EFO=90°,
∵∠DOH=∠BOE,
∴∠HDF=∠OEF,
∵DE=BE,
∴∠EDO=∠EBO,
∵BD平分∠HDE,
∴∠HDF=∠BDE,
∴∠OEF=∠OBE,
∵∠OEF+∠EOF=90°,
∴∠EOF+∠EBO=90°,
∴∠BEO=90°,
∴BE⊥AC,
∴BA=BC.
30.(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)∵四边形ABEF是正方形,
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∵AD=AE,
∴AD﹣AF=AE﹣AG,
即DF=EG,
在△DFO和△EGO中,,
∴△DFO≌△EGO(AAS),
∴FO=GO,FD=EG
∵∠DAE=∠AEF=45°,∠AFE=∠AGD=90°,
∴DF=FO=OG=EG,
∴DOOFOG,
∴DG=DO+OGOG+OG=1,
∴OG1,
∴OD(1)=2.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
