圆单元测试-数学六年级上册人教版(含解析)
文档属性
| 名称 | 圆单元测试-数学六年级上册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 20:57:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
圆单元测试-数学六年级上册人教版
一、选择题
1.一个圆的半径是5厘米,这个圆的周长是( )厘米。
A.5π B.25π C.100π D.10π
2.下列说法正确的是( )。
A.任何数都有倒数 B.半径等于直径的
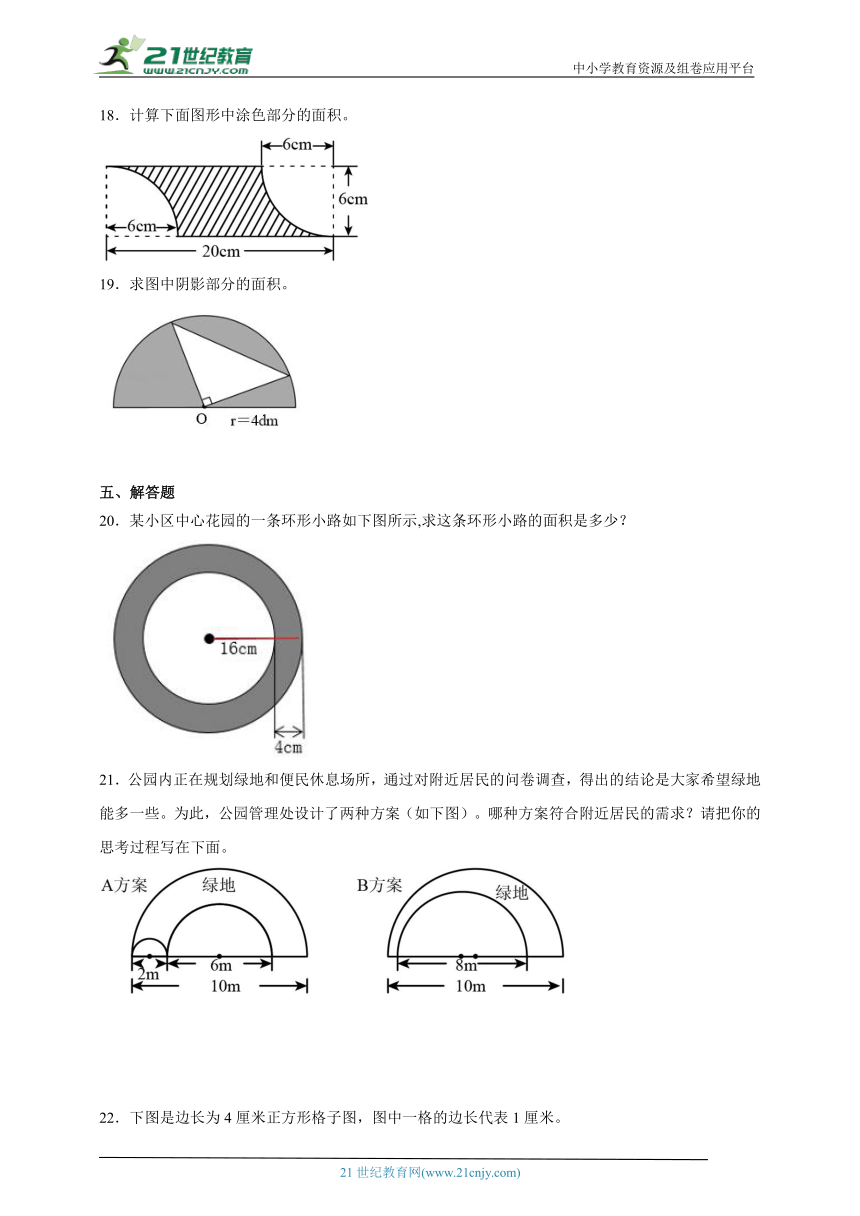
C.的大小与圆的大小无关 D.假分数的倒数一定比1小
3.下图是一个半圆,它的半径是5cm,周长是( )cm。
A.5π B.5π+10
C.10π D.10π+10
4.把一个圆分成32等份,拼成一个和它面积相等的近似的长方形(如下图),拼成的图形的周长是8.28cm,圆的面积是( )。
A.3.14 B.6.28 C.12.56 D.50.24
5.在图中画一个最大的正方形,如图所示,已知阴影部分的面积为a平方厘米,则圆的面积是( )平方厘米.
A.2aπ B.πa C.4a+π D.4a+
6.如图,如果让小圆紧贴着大圆的边缘滚动一周,小圆的圆心移动的路程是( )厘米。
A. B. C. D.
二、填空题
7.把一个圆形纸片折成一个最大的正方形,这个正方形的对角线长8cm,那么这个圆形纸片的面积是( )平方厘米,折起来的部分的面积是( )平方厘米。
8.在一张长6cm,宽4cm的长方形纸片上,剪下一个最大的圆,这个圆的周长是( )cm,剩下纸片的面积是( )cm2。
9.图中阴影面积是甲圆面积的,是乙圆面积的,乙圆面积是甲圆面积的( )。
10.绍兴市市心路绿化带的自动旋转喷灌装置的最远射程是3米,它的最大喷灌面积是( )平方米。
11.大圆的半径是6厘米,小圆的半径是4厘米,大圆和小圆的周长之比是( )∶( ),面积之比是( )∶( )。
12.把一个圆沿半径分成若干(偶数)等份,拼成的一个近似的长方形,圆的周长与长方形的周长相差6厘米,这个圆的面积是( )平方厘米,周长是( )厘米。
三、判断题
13.两个圆的半径分别是3cm和4cm,它们的面积之比和周长之比都是3∶4。( )
14.一个扇形的圆心角是90°,则这个扇形的面积是同半径圆面积的。( )
15.把周长是6.28cm的圆形纸片对折成一个半圆,那么半圆的周长是3.14cm。( )
16.在同一圆中,半圆的面积是圆面积的一半,半圆的周长也是圆周长的一半。( )
17.一个半圆的周长是20.56厘米,这个半圆的直径是8厘米。( )
四、图形计算
18.计算下面图形中涂色部分的面积。
19.求图中阴影部分的面积。
五、解答题
20.某小区中心花园的一条环形小路如下图所示,求这条环形小路的面积是多少?
21.公园内正在规划绿地和便民休息场所,通过对附近居民的问卷调查,得出的结论是大家希望绿地能多一些。为此,公园管理处设计了两种方案(如下图)。哪种方案符合附近居民的需求?请把你的思考过程写在下面。
22.下图是边长为4厘米正方形格子图,图中一格的边长代表1厘米。
(1)在上边正方形格子图中,以O为圆心,画一个直径为4厘米的圆。
(2)请你求出正方形与圆之间部分的面积。
23.下图是一个“禁止驶入”的交通标志,标志中有一个长70cm、宽12cm的白色长方形,其余部分是红色。请你算一算,这个交通标志中红色部分的面积是多少平方厘米?
24.小明用一样大小的两张正方形纸设计了以下两个图案(阴影部分).这两个图案的面积一样大吗?为什么?
参考答案:
1.D
【分析】根据圆的周长公式,直接选择正确选项即可。
【详解】2×π×5=10π(厘米),所以这个圆的周长是10π厘米。
故答案为:D
【点睛】本题考查了圆的周长,掌握圆的周长公式是解题的关键。
2.C
【解析】略
3.B
【详解】一个半圆的半径是5cm,利用圆的周长公式:可求出圆的周长,再除以2可求出圆周长的一半,再加上直径的长度,就是它的周长。
【解答】解:
故答案为:B
【点睛】本题的重点是让学生理解半圆的周长圆周长的一半直径。
4.A
【分析】把一个圆分成32等份,拼成一个和它面积相等的近似的长方形,长方形的长=圆周长的一半,长方形的宽=圆的半径,根据长方形周长=(长+宽)×2,列出方程求出r,再根据圆的面积=πr2,求出面积即可。
【详解】(3.14r+r)×2=8.28
解:(3.14r+r)×2÷2=8.28÷2
4.14r=4.14
4.14r÷4.14=4.14÷4.14
r=1
3.14×12
=3.14×1
=3.14()
圆的面积是3.14。
故答案为:A
【点睛】关键是熟悉圆的面积公式推导过程。
5.A
【详解】试题分析:因为阴影部分是一个等腰直角三角形,两条直角边等于圆的半径,设出圆的半径,则阴影部分面积,=r×r÷2,即可计算出圆的半径的平方,代入圆的面积公式计算即可.
解:设圆的半径为r,则阴影部分面积为:
r2÷2=a,所以r2=2a(平方厘米),
圆的面积为:π×2a=2aπ(平方厘米).
故选A.
点评:解决本题的关键是明确阴影部分是一个等腰直角三角形,两条直角边等于圆的半径,求出圆的半径的平方.
6.D
【分析】小圆的圆心走过的路程是半径为(2+1)厘米的圆的周长,由此利用圆的周长公式解答即可。
【详解】2××(2+1)
=2×3×
=6(厘米)
即小圆的圆心移动的路程是6厘米。
故答案为:D
【点睛】本题主要是利用圆的周长公式解决生活中的实际问题。
7. 50.24 18.24
【分析】把一个圆形纸片折成一个最大的正方形,这个正方形的对角线=圆的直径,根据圆的面积=πr2,求出圆形纸片的面积;圆的面积-正方形面积=折起来的面积,正方形的面积=两个三角形面积和,据此列式计算。
【详解】3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24(平方厘米)
50.24-8×(8÷2)÷2×2
=50.24-8×4÷2×2
=50.24-32
=18.24(平方厘米)
这个圆形纸片的面积是50.24平方厘米,折起来的部分的面积是18.24平方厘米。
【点睛】关键是掌握并灵活运用圆的面积公式,灵活计算正方形面积。
8. 12.56 11.44
【分析】先确定圆的大小,即圆的半径,然后长方形面积减去圆的面积。
【详解】如图所示:
圆的直径是4cm,半径是2cm;
【点睛】在长方形中画最大的圆,圆的直径是长方形的宽,类似于木桶原理。
9.
【分析】假定甲圆面积是单位“1”,那么阴影部分的面积是,乙圆面积=阴影部分面积÷,最后,用乙圆面积除以甲圆面积,求出乙圆面积是甲圆面积的几分之几即可。
【详解】÷÷1=
所以,乙圆面积是甲圆面积的。
【点睛】本题考查了分数除法,求一个数是另一个数的几分之几,用除法。
10.28.26
【分析】自动旋转一周就是一个圆形,最远射程也就是半径,最大喷灌面积也就是圆的面积,根据圆的面积公式即可解答。
【详解】最大喷灌面积=π×半径×半径
=3.14×3×3
=28.26(平方米)
【点睛】本题主要考查圆的面积公式的运用。
11. 3 2 9 4
【分析】假设大圆的半径为R,小圆的半径为r,根据圆的周长=2πr,分别表示出两个圆的周长,写出周长比化简即可;根据圆的面积=πr2,分别表示出两个圆的面积,写出面积比化简即可。
【详解】假设大圆的半径为R,小圆的半径为r。
2πR∶2πr
=(2πR÷2π)∶(2πr÷2π)
=R∶r
=6∶4
=3∶2
πR2∶πr2,
=(πR2÷π)∶(πr2÷π),
=R2∶r2
=62∶42
=36∶16
=9∶4
大圆周长和小圆周长的比是3∶2,大圆和小圆的面积比是9∶4。
【点睛】关键是掌握并灵活运用圆的周长和面积公式,理解比的意义。
12. 28.26 18.84
【分析】由图形可知,长方形的长等于圆的周长的一半,则长方形的宽等于圆的半径。圆的周长与长方形的周长相差6厘米,根据圆周长和长方形的周长公式,可知圆的周长与长方形的周长相差两个半径,所以长方形两条宽的和为6厘米,长方形宽为3厘米,即圆的半径为3厘米。根据圆的面积公式S=πr2和周长公式C=2πr即可得出答案。
【详解】6÷2=3(厘米)
圆的周长与长方形的周长相差6厘米,所以长方形的两条宽的和为6厘米,长方形的宽为3厘米,则圆的半径为3厘米。
圆的面积是:3.14×32
=3.14×9
=28.26(平方厘米
圆的周长是:2×3.14×3
=6.28×3
=18.84(厘米
圆的面积为28.26平方厘米,圆的周长为18.84厘米。
【点睛】解答本题的关键是:根据图形判断出圆的周长和长方形的周长差就是圆的两条半径的和。
13.×
【详解】略
14.√
【分析】周角的度数为360°,扇形的圆心角度占总角度的,因此面积也是同半径圆面积的,由此解答即可。
【详解】一个扇形的圆心角是90°,则这个扇形的面积是同半径圆面积的,原题说法正确;
故答案为:√
【点睛】解答本题的关键是抓住扇形圆心角和周角的关系,进而判断面积关系。
15.×
【分析】半圆的周长比圆周长的一半多一条直径的长度,根据圆的周长公式:C=πd,据此解答。
【详解】6.28÷2+6.28÷3.14
=3.14+2
=5.14(cm)
所以,半圆的周长是5.14cm。
故答案为:×
【点睛】理解半圆和圆周长的一半的区别是解答题目的关键。
16.×
【分析】根据半圆面积=圆面积÷2,半圆周长=圆周长÷2+直径。据此判断即可。
【详解】由分析可知:
在同圆或等圆内,半圆的面积是圆面积的一半,半圆的周长不是圆周长的一半。原题干说法错误。
故答案为:×
【点睛】本题考查半圆的面积和周长,明确半圆的周长的计算方法是解题的关键。
17.√
【分析】半圆的周长等于整圆周长的一半,再加上一条直径的长度,根据圆的周长公式:C=πd,据此计算即可。
【详解】3.14×8÷2+8
=25.12÷2+8
=12.56+8
=20.56(厘米)
则原题干说法正确。
故答案为:√
【点睛】本题考查半圆的周长,明确半圆的周长的计算方法是解题的关键。
18.63.48平方厘米
【分析】图中虚线部分是两个圆心角是90°,半径是6厘米的扇形,因为半径相等,两个扇形刚好拼成一个半圆,用长方形面积减去半圆的面积,就能求出涂色部分的面积。
【详解】
=120-56.52
(平方厘米)
19.17.12dm2
【分析】看图,半圆的半径是4dm,三角形的底和高均是4dm。半圆面积=圆面积÷2,圆面积=3.14×半径2,三角形面积=底×高÷2,据此先分别求出半圆和三角形的面积,再将半圆面积减去三角形面积,即可求出阴影部分的面积。
【详解】3.14×42÷2-4×4÷2
=50.24÷2-8
=25.12-8
=17.12(dm2)
所以,阴影部分的面积是17.12dm2。
20.351.68平方厘米
【详解】R=16(cm)
r =16-4=12(cm)
=3.14×(16×16-12×12)
=3.14×(256-144)
=3.14×112
=351.68(cm )
答:这条环形小路的面积是351.68平方厘米。
21.A方案;思考过程见详解
【分析】A方案的绿地面积=直径为10米半圆的面积-直径为6米半圆的面积-直径为2米半圆的面积,B方案的绿地面积=直径为10米半圆的面积-直径为8米半圆的面积,利用“”求出两种方案绿地的面积,最后比较大小,据此解答。
【详解】A方案:
=
=
=
=(平方米)
B方案:
=
=
=
=(平方米)
因为>,所以A方案绿地面积多一些更符合居民的需求。
答:A方案符合附近居民的需求。
【点睛】熟练掌握圆的面积计算公式并求出两种方案绿地的面积是解答题目的关键。
22.(1)图见详解
(2)3.44平方厘米
【分析】(1)根据圆的画法,以点O为圆心,以(4÷2)厘米为半径;画一个圆即可。
(2)求出正方形和圆之间部分的面积,就是边长为4厘米的正方形面积-半径是(4÷2)厘米圆的面积;根据正方形面积=边长×边长;圆的面积=πr2;代入数据,即可解答。
【详解】(1)4÷2=2(厘米)
作图如下:
(2)正方形的面积:4×4=16(平方厘米)
圆的面积:3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
16-12.56=3.44(平方厘米)
答:正方形与圆之间部分的面积是3.44平方厘米。
【点睛】解答本题的关键明确正方形面积公式和圆的面积公式进行解答。
23.4184平方厘米
【分析】根据图意可知,红色面积(阴影部分面积)=圆面积-长方形面积,代入数据求解。
【详解】3.14×(80÷2) -70×12
=3.14×1600-840
=5024-840
=4184(平方厘米)
答:这个交通标志中红色部分的面积是4184平方厘米。
【点睛】此题考查的是求阴影部分面积,明确是阴影部分由那些基本图形的和或差组成的是解题关键。
24.一样大,理由见解析.
【详解】解:设正方形边长为4a.
图一阴影部分面积为:
图二阴影部分面积为:
所以,两个图案阴影部分面积一样大.
【点睛】考察了不规则图形面积的计算方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆单元测试-数学六年级上册人教版
一、选择题
1.一个圆的半径是5厘米,这个圆的周长是( )厘米。
A.5π B.25π C.100π D.10π
2.下列说法正确的是( )。
A.任何数都有倒数 B.半径等于直径的
C.的大小与圆的大小无关 D.假分数的倒数一定比1小
3.下图是一个半圆,它的半径是5cm,周长是( )cm。
A.5π B.5π+10
C.10π D.10π+10
4.把一个圆分成32等份,拼成一个和它面积相等的近似的长方形(如下图),拼成的图形的周长是8.28cm,圆的面积是( )。
A.3.14 B.6.28 C.12.56 D.50.24
5.在图中画一个最大的正方形,如图所示,已知阴影部分的面积为a平方厘米,则圆的面积是( )平方厘米.
A.2aπ B.πa C.4a+π D.4a+
6.如图,如果让小圆紧贴着大圆的边缘滚动一周,小圆的圆心移动的路程是( )厘米。
A. B. C. D.
二、填空题
7.把一个圆形纸片折成一个最大的正方形,这个正方形的对角线长8cm,那么这个圆形纸片的面积是( )平方厘米,折起来的部分的面积是( )平方厘米。
8.在一张长6cm,宽4cm的长方形纸片上,剪下一个最大的圆,这个圆的周长是( )cm,剩下纸片的面积是( )cm2。
9.图中阴影面积是甲圆面积的,是乙圆面积的,乙圆面积是甲圆面积的( )。
10.绍兴市市心路绿化带的自动旋转喷灌装置的最远射程是3米,它的最大喷灌面积是( )平方米。
11.大圆的半径是6厘米,小圆的半径是4厘米,大圆和小圆的周长之比是( )∶( ),面积之比是( )∶( )。
12.把一个圆沿半径分成若干(偶数)等份,拼成的一个近似的长方形,圆的周长与长方形的周长相差6厘米,这个圆的面积是( )平方厘米,周长是( )厘米。
三、判断题
13.两个圆的半径分别是3cm和4cm,它们的面积之比和周长之比都是3∶4。( )
14.一个扇形的圆心角是90°,则这个扇形的面积是同半径圆面积的。( )
15.把周长是6.28cm的圆形纸片对折成一个半圆,那么半圆的周长是3.14cm。( )
16.在同一圆中,半圆的面积是圆面积的一半,半圆的周长也是圆周长的一半。( )
17.一个半圆的周长是20.56厘米,这个半圆的直径是8厘米。( )
四、图形计算
18.计算下面图形中涂色部分的面积。
19.求图中阴影部分的面积。
五、解答题
20.某小区中心花园的一条环形小路如下图所示,求这条环形小路的面积是多少?
21.公园内正在规划绿地和便民休息场所,通过对附近居民的问卷调查,得出的结论是大家希望绿地能多一些。为此,公园管理处设计了两种方案(如下图)。哪种方案符合附近居民的需求?请把你的思考过程写在下面。
22.下图是边长为4厘米正方形格子图,图中一格的边长代表1厘米。
(1)在上边正方形格子图中,以O为圆心,画一个直径为4厘米的圆。
(2)请你求出正方形与圆之间部分的面积。
23.下图是一个“禁止驶入”的交通标志,标志中有一个长70cm、宽12cm的白色长方形,其余部分是红色。请你算一算,这个交通标志中红色部分的面积是多少平方厘米?
24.小明用一样大小的两张正方形纸设计了以下两个图案(阴影部分).这两个图案的面积一样大吗?为什么?
参考答案:
1.D
【分析】根据圆的周长公式,直接选择正确选项即可。
【详解】2×π×5=10π(厘米),所以这个圆的周长是10π厘米。
故答案为:D
【点睛】本题考查了圆的周长,掌握圆的周长公式是解题的关键。
2.C
【解析】略
3.B
【详解】一个半圆的半径是5cm,利用圆的周长公式:可求出圆的周长,再除以2可求出圆周长的一半,再加上直径的长度,就是它的周长。
【解答】解:
故答案为:B
【点睛】本题的重点是让学生理解半圆的周长圆周长的一半直径。
4.A
【分析】把一个圆分成32等份,拼成一个和它面积相等的近似的长方形,长方形的长=圆周长的一半,长方形的宽=圆的半径,根据长方形周长=(长+宽)×2,列出方程求出r,再根据圆的面积=πr2,求出面积即可。
【详解】(3.14r+r)×2=8.28
解:(3.14r+r)×2÷2=8.28÷2
4.14r=4.14
4.14r÷4.14=4.14÷4.14
r=1
3.14×12
=3.14×1
=3.14()
圆的面积是3.14。
故答案为:A
【点睛】关键是熟悉圆的面积公式推导过程。
5.A
【详解】试题分析:因为阴影部分是一个等腰直角三角形,两条直角边等于圆的半径,设出圆的半径,则阴影部分面积,=r×r÷2,即可计算出圆的半径的平方,代入圆的面积公式计算即可.
解:设圆的半径为r,则阴影部分面积为:
r2÷2=a,所以r2=2a(平方厘米),
圆的面积为:π×2a=2aπ(平方厘米).
故选A.
点评:解决本题的关键是明确阴影部分是一个等腰直角三角形,两条直角边等于圆的半径,求出圆的半径的平方.
6.D
【分析】小圆的圆心走过的路程是半径为(2+1)厘米的圆的周长,由此利用圆的周长公式解答即可。
【详解】2××(2+1)
=2×3×
=6(厘米)
即小圆的圆心移动的路程是6厘米。
故答案为:D
【点睛】本题主要是利用圆的周长公式解决生活中的实际问题。
7. 50.24 18.24
【分析】把一个圆形纸片折成一个最大的正方形,这个正方形的对角线=圆的直径,根据圆的面积=πr2,求出圆形纸片的面积;圆的面积-正方形面积=折起来的面积,正方形的面积=两个三角形面积和,据此列式计算。
【详解】3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24(平方厘米)
50.24-8×(8÷2)÷2×2
=50.24-8×4÷2×2
=50.24-32
=18.24(平方厘米)
这个圆形纸片的面积是50.24平方厘米,折起来的部分的面积是18.24平方厘米。
【点睛】关键是掌握并灵活运用圆的面积公式,灵活计算正方形面积。
8. 12.56 11.44
【分析】先确定圆的大小,即圆的半径,然后长方形面积减去圆的面积。
【详解】如图所示:
圆的直径是4cm,半径是2cm;
【点睛】在长方形中画最大的圆,圆的直径是长方形的宽,类似于木桶原理。
9.
【分析】假定甲圆面积是单位“1”,那么阴影部分的面积是,乙圆面积=阴影部分面积÷,最后,用乙圆面积除以甲圆面积,求出乙圆面积是甲圆面积的几分之几即可。
【详解】÷÷1=
所以,乙圆面积是甲圆面积的。
【点睛】本题考查了分数除法,求一个数是另一个数的几分之几,用除法。
10.28.26
【分析】自动旋转一周就是一个圆形,最远射程也就是半径,最大喷灌面积也就是圆的面积,根据圆的面积公式即可解答。
【详解】最大喷灌面积=π×半径×半径
=3.14×3×3
=28.26(平方米)
【点睛】本题主要考查圆的面积公式的运用。
11. 3 2 9 4
【分析】假设大圆的半径为R,小圆的半径为r,根据圆的周长=2πr,分别表示出两个圆的周长,写出周长比化简即可;根据圆的面积=πr2,分别表示出两个圆的面积,写出面积比化简即可。
【详解】假设大圆的半径为R,小圆的半径为r。
2πR∶2πr
=(2πR÷2π)∶(2πr÷2π)
=R∶r
=6∶4
=3∶2
πR2∶πr2,
=(πR2÷π)∶(πr2÷π),
=R2∶r2
=62∶42
=36∶16
=9∶4
大圆周长和小圆周长的比是3∶2,大圆和小圆的面积比是9∶4。
【点睛】关键是掌握并灵活运用圆的周长和面积公式,理解比的意义。
12. 28.26 18.84
【分析】由图形可知,长方形的长等于圆的周长的一半,则长方形的宽等于圆的半径。圆的周长与长方形的周长相差6厘米,根据圆周长和长方形的周长公式,可知圆的周长与长方形的周长相差两个半径,所以长方形两条宽的和为6厘米,长方形宽为3厘米,即圆的半径为3厘米。根据圆的面积公式S=πr2和周长公式C=2πr即可得出答案。
【详解】6÷2=3(厘米)
圆的周长与长方形的周长相差6厘米,所以长方形的两条宽的和为6厘米,长方形的宽为3厘米,则圆的半径为3厘米。
圆的面积是:3.14×32
=3.14×9
=28.26(平方厘米
圆的周长是:2×3.14×3
=6.28×3
=18.84(厘米
圆的面积为28.26平方厘米,圆的周长为18.84厘米。
【点睛】解答本题的关键是:根据图形判断出圆的周长和长方形的周长差就是圆的两条半径的和。
13.×
【详解】略
14.√
【分析】周角的度数为360°,扇形的圆心角度占总角度的,因此面积也是同半径圆面积的,由此解答即可。
【详解】一个扇形的圆心角是90°,则这个扇形的面积是同半径圆面积的,原题说法正确;
故答案为:√
【点睛】解答本题的关键是抓住扇形圆心角和周角的关系,进而判断面积关系。
15.×
【分析】半圆的周长比圆周长的一半多一条直径的长度,根据圆的周长公式:C=πd,据此解答。
【详解】6.28÷2+6.28÷3.14
=3.14+2
=5.14(cm)
所以,半圆的周长是5.14cm。
故答案为:×
【点睛】理解半圆和圆周长的一半的区别是解答题目的关键。
16.×
【分析】根据半圆面积=圆面积÷2,半圆周长=圆周长÷2+直径。据此判断即可。
【详解】由分析可知:
在同圆或等圆内,半圆的面积是圆面积的一半,半圆的周长不是圆周长的一半。原题干说法错误。
故答案为:×
【点睛】本题考查半圆的面积和周长,明确半圆的周长的计算方法是解题的关键。
17.√
【分析】半圆的周长等于整圆周长的一半,再加上一条直径的长度,根据圆的周长公式:C=πd,据此计算即可。
【详解】3.14×8÷2+8
=25.12÷2+8
=12.56+8
=20.56(厘米)
则原题干说法正确。
故答案为:√
【点睛】本题考查半圆的周长,明确半圆的周长的计算方法是解题的关键。
18.63.48平方厘米
【分析】图中虚线部分是两个圆心角是90°,半径是6厘米的扇形,因为半径相等,两个扇形刚好拼成一个半圆,用长方形面积减去半圆的面积,就能求出涂色部分的面积。
【详解】
=120-56.52
(平方厘米)
19.17.12dm2
【分析】看图,半圆的半径是4dm,三角形的底和高均是4dm。半圆面积=圆面积÷2,圆面积=3.14×半径2,三角形面积=底×高÷2,据此先分别求出半圆和三角形的面积,再将半圆面积减去三角形面积,即可求出阴影部分的面积。
【详解】3.14×42÷2-4×4÷2
=50.24÷2-8
=25.12-8
=17.12(dm2)
所以,阴影部分的面积是17.12dm2。
20.351.68平方厘米
【详解】R=16(cm)
r =16-4=12(cm)
=3.14×(16×16-12×12)
=3.14×(256-144)
=3.14×112
=351.68(cm )
答:这条环形小路的面积是351.68平方厘米。
21.A方案;思考过程见详解
【分析】A方案的绿地面积=直径为10米半圆的面积-直径为6米半圆的面积-直径为2米半圆的面积,B方案的绿地面积=直径为10米半圆的面积-直径为8米半圆的面积,利用“”求出两种方案绿地的面积,最后比较大小,据此解答。
【详解】A方案:
=
=
=
=(平方米)
B方案:
=
=
=
=(平方米)
因为>,所以A方案绿地面积多一些更符合居民的需求。
答:A方案符合附近居民的需求。
【点睛】熟练掌握圆的面积计算公式并求出两种方案绿地的面积是解答题目的关键。
22.(1)图见详解
(2)3.44平方厘米
【分析】(1)根据圆的画法,以点O为圆心,以(4÷2)厘米为半径;画一个圆即可。
(2)求出正方形和圆之间部分的面积,就是边长为4厘米的正方形面积-半径是(4÷2)厘米圆的面积;根据正方形面积=边长×边长;圆的面积=πr2;代入数据,即可解答。
【详解】(1)4÷2=2(厘米)
作图如下:
(2)正方形的面积:4×4=16(平方厘米)
圆的面积:3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
16-12.56=3.44(平方厘米)
答:正方形与圆之间部分的面积是3.44平方厘米。
【点睛】解答本题的关键明确正方形面积公式和圆的面积公式进行解答。
23.4184平方厘米
【分析】根据图意可知,红色面积(阴影部分面积)=圆面积-长方形面积,代入数据求解。
【详解】3.14×(80÷2) -70×12
=3.14×1600-840
=5024-840
=4184(平方厘米)
答:这个交通标志中红色部分的面积是4184平方厘米。
【点睛】此题考查的是求阴影部分面积,明确是阴影部分由那些基本图形的和或差组成的是解题关键。
24.一样大,理由见解析.
【详解】解:设正方形边长为4a.
图一阴影部分面积为:
图二阴影部分面积为:
所以,两个图案阴影部分面积一样大.
【点睛】考察了不规则图形面积的计算方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
