2024北师大版数学九年级下学期课时练--专项素养综合全练(七)与圆有关的阴影部分面积的计算(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--专项素养综合全练(七)与圆有关的阴影部分面积的计算(含解析) | 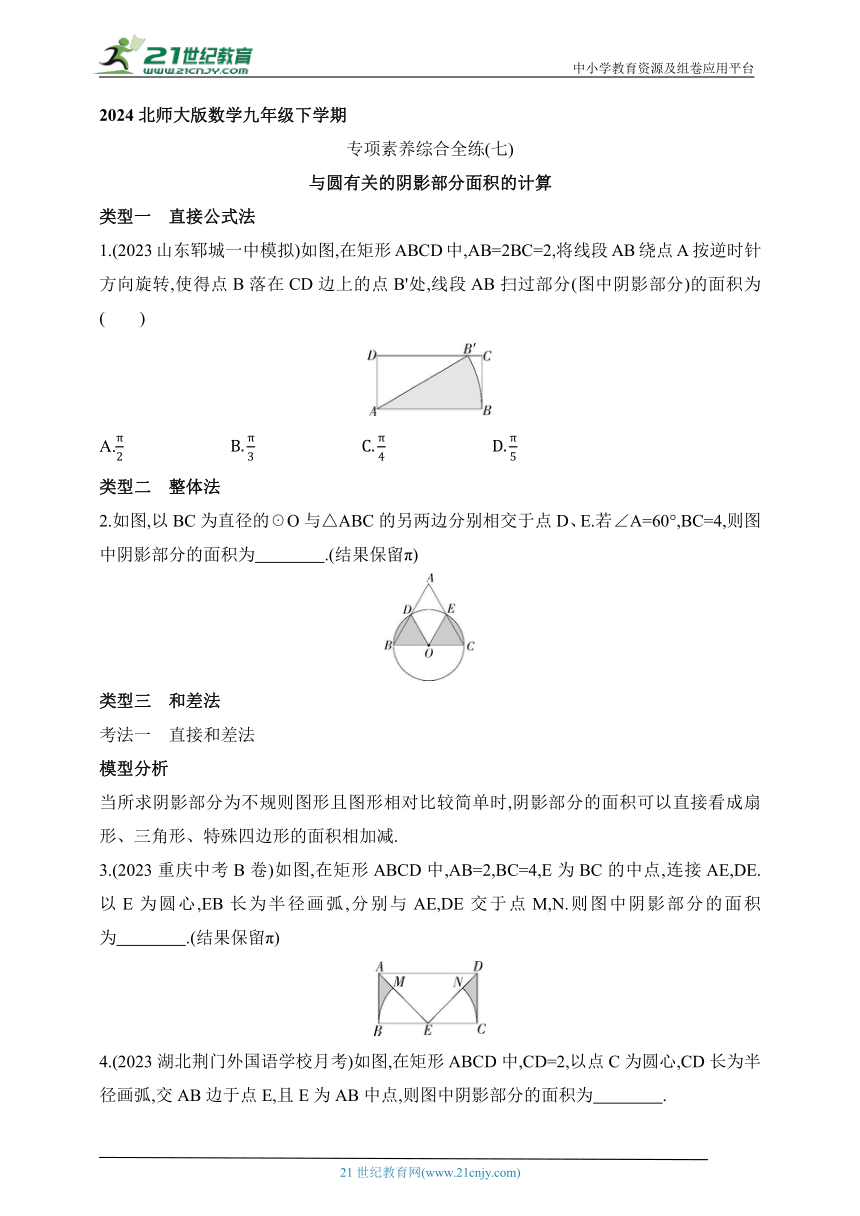 | |
| 格式 | docx | ||
| 文件大小 | 512.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 12:52:36 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
专项素养综合全练(七)
与圆有关的阴影部分面积的计算
类型一 直接公式法
1.(2023山东郓城一中模拟)如图,在矩形ABCD中,AB=2BC=2,将线段AB绕点A按逆时针方向旋转,使得点B落在CD边上的点B'处,线段AB扫过部分(图中阴影部分)的面积为( )
A.
类型二 整体法
2.如图,以BC为直径的☉O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为 .(结果保留π)
类型三 和差法
考法一 直接和差法
模型分析
当所求阴影部分为不规则图形且图形相对比较简单时,阴影部分的面积可以直接看成扇形、三角形、特殊四边形的面积相加减.
3.(2023重庆中考B卷)如图,在矩形ABCD中,AB=2,BC=4,E为BC的中点,连接AE,DE.以E为圆心,EB长为半径画弧,分别与AE,DE交于点M,N.则图中阴影部分的面积为 .(结果保留π)
4.(2023湖北荆门外国语学校月考)如图,在矩形ABCD中,CD=2,以点C为圆心,CD长为半径画弧,交AB边于点E,且E为AB中点,则图中阴影部分的面积为 .
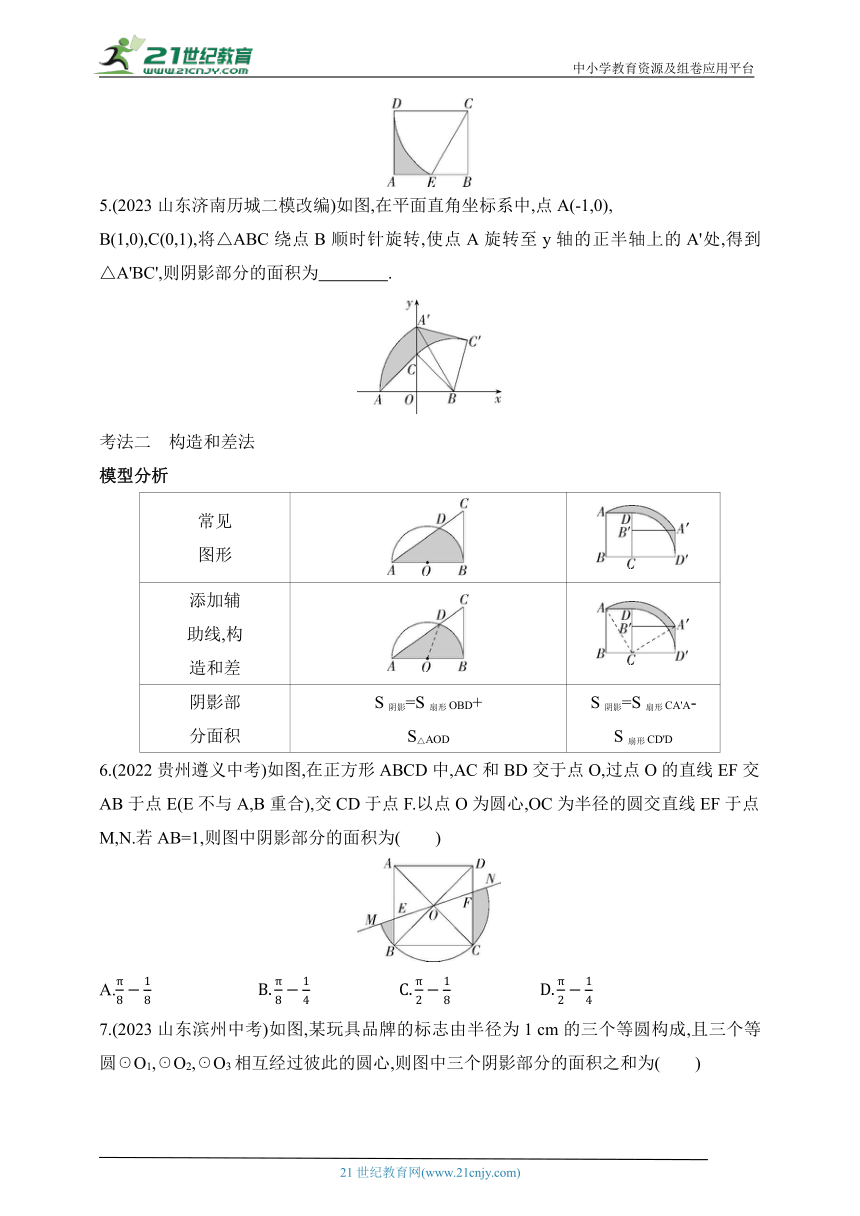
5.(2023山东济南历城二模改编)如图,在平面直角坐标系中,点A(-1,0),
B(1,0),C(0,1),将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A'处,得到△A'BC',则阴影部分的面积为 .
考法二 构造和差法
模型分析
常见 图形
添加辅 助线,构 造和差
阴影部 分面积 S阴影=S扇形OBD+ S△AOD S阴影=S扇形CA'A- S扇形CD'D
6.(2022贵州遵义中考)如图,在正方形ABCD中,AC和BD交于点O,过点O的直线EF交AB于点E(E不与A,B重合),交CD于点F.以点O为圆心,OC为半径的圆交直线EF于点M,N.若AB=1,则图中阴影部分的面积为( )
A.
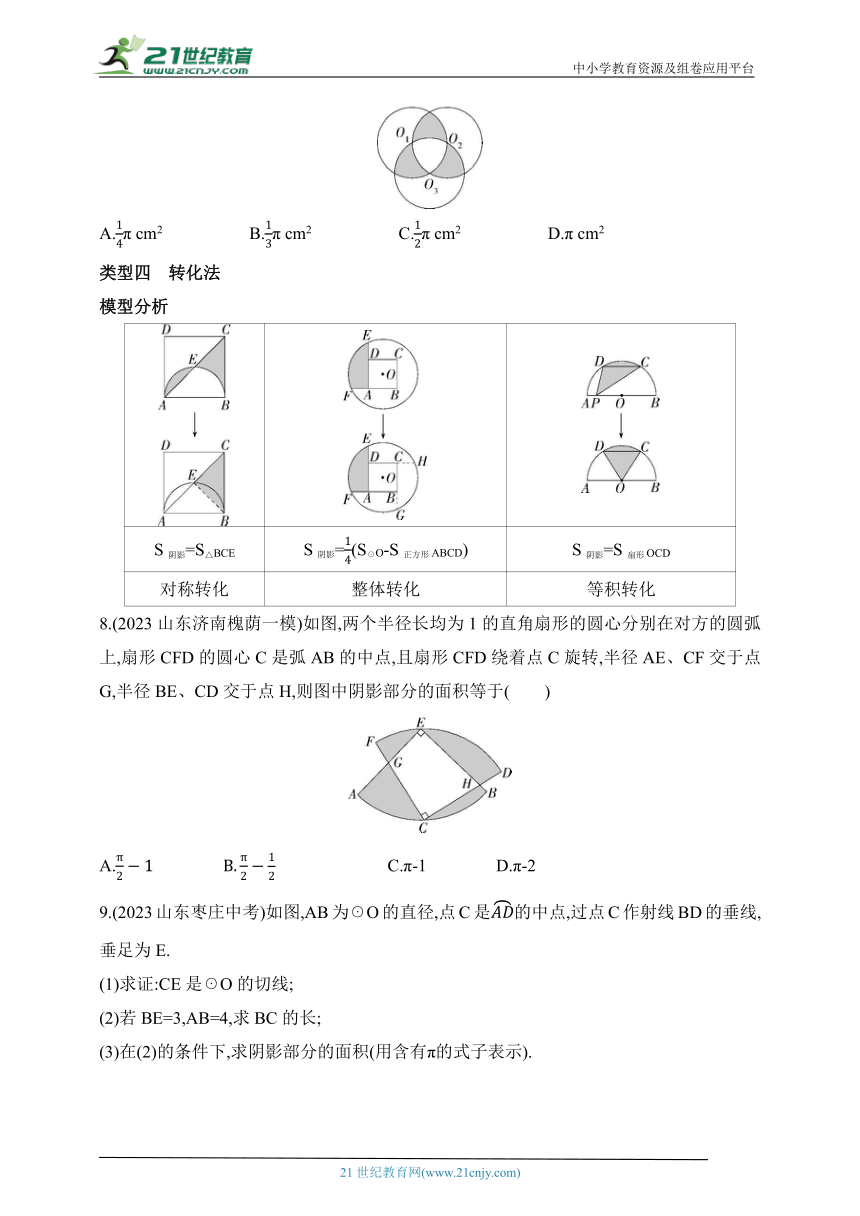
7.(2023山东滨州中考)如图,某玩具品牌的标志由半径为1 cm的三个等圆构成,且三个等圆☉O1,☉O2,☉O3相互经过彼此的圆心,则图中三个阴影部分的面积之和为( )
A.π cm2 B.π cm2 C.π cm2 D.π cm2
类型四 转化法
模型分析
S阴影=S△BCE S阴影=(S☉O-S正方形ABCD) S阴影=S扇形OCD
对称转化 整体转化 等积转化
8.(2023山东济南槐荫一模)如图,两个半径长均为1的直角扇形的圆心分别在对方的圆弧上,扇形CFD的圆心C是弧AB的中点,且扇形CFD绕着点C旋转,半径AE、CF交于点G,半径BE、CD交于点H,则图中阴影部分的面积等于( )
A. C.π-1 D.π-2
9.(2023山东枣庄中考)如图,AB为☉O的直径,点C是的中点,过点C作射线BD的垂线,垂足为E.
(1)求证:CE是☉O的切线;
(2)若BE=3,AB=4,求BC的长;
(3)在(2)的条件下,求阴影部分的面积(用含有π的式子表示).
类型五 容斥原理法
模型分析
有的阴影部分面积是由两个基本图形相互重叠得到的.常用的方法是被重叠图形的面积=两个基本图形的面积之和-组合图形的面积.
如图,S阴影=S扇形CAE+S扇形CBD-S△ABC.
10.已知AB为半圆O的直径,且AB=4,点P是的中点.如图,过点A作半圆O的切线AC,与BP的延长线交于点C,以点C为圆心,AC长为半径画弧交BC于点D,则图中阴影部分的面积是 .
答案全解全析
1.B ∵AB=2BC=2,∴BC=1,
∵四边形ABCD是矩形,∴AD=BC=1,∠D=∠DAB=90°,
由旋转可得AB'=AB=2,∴cos∠DAB'=,∴∠DAB'=60°,
∴∠BAB'=30°,∴线段AB扫过部分的面积=,故选B.
2.π
解析 ∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵△OBD、△OCE是等腰三角形,
∴∠BDO+∠CEO=∠ABC+∠ACB=120°,
∴∠BOD+∠COE=360°-(∠BDO+∠CEO)-(∠ABC+∠ACB)=360°-120°-120°=120°,
∵BC=4,∴OB=OC=2,∴S阴影=π.
3.4-π
解析 ∵四边形ABCD为矩形,AB=2,
∴∠ABC=∠DCB=90°,CD=AB=2,
∵BC=4,E为BC的中点,
∴BE=CE=2,
∴AB=BE,CD=CE,
∴∠BAE=∠AEB=∠CDE=∠DEC=45°,
∴阴影部分的面积为2×=4-π.
4.
解析 ∵四边形ABCD为矩形,∴AB=CD=2,∠B=∠DCB=90°,
∵E为AB中点,∴EB=AB=1,
由作图可知CE=CD=2,∴∠ECB=30°,∴∠DCE=60°,
∵EB=1,CE=2,∴由勾股定理可知BC=,
∴阴影部分的面积=S矩形ABCD-S△CBE-S扇形ECD=.
5.
解析 ∵点A(-1,0),B(1,0),C(0,1),∴OA=OB=OC=1,
∴BC=,AB=2,
由旋转可知BA'=BA=2,
又OB=1,∴∠OA'B=30°,∴∠ABA'=90°-30°=60°=∠CBC',
∴S阴影=S扇形BAA'+S△BA'C'-S扇形BCC'-S△ABC =S扇形BAA'-S扇形BCC' = =.
6.B 如图,以O为圆心,OD为半径作弧DN,
易知OD=,S△OBE=S△ODF,S扇形BOM=S扇形DON,
∴S1=S2,∴S阴影=S扇形DOC-S△DOC=,故选B.
模型分析 当所求阴影部分为不规则图形,且图形相对比较复杂,不能直接看成规则图形的面积和差时,常通过“分割求和”“整体作差”等方法,添加适当的辅助线,构造扇形、三角形或特殊四边形,然后把它们的面积相加减.构造图形时一般先观察阴影部分图形:①若阴影部分图形有一部分是弧线,则需找出弧线所对应的圆心,连半径构造扇形;
②若阴影部分是由图形旋转而成的,则旋转中心即为圆心,将旋转前后的对应点分别与旋转中心连接构造扇形.
7.C 如图所示,连接O1A,O2A,O1B,O3B,O2C,O3C,O1O2,O1O3,O2O3,则△O1AO2,△O1BO3,△O2CO3,△O1O2O3是边长为1 cm的正三角形,所以S阴影=3(cm2),故选C.
8.A 两扇形的面积和为π,连接CE,过点C作CM⊥AE,作CN⊥BE,垂足分别为M、N,则四边形EMCN是矩形,∴∠MCN=
90°,∴∠MCG+∠FCN=90°,∵∠NCH+∠FCN=90°,∴∠MCG=∠NCH,∵点C是弧AB的中点,∴EC平分∠AEB,∴CM=CN,∴矩形EMCN是正方形,在△CMG与△CNH中,∴△CMG≌△CNH(ASA),∴图中空白区域面积等于对角线长是1的正方形面积,∴空白区域的面积为,
∴图中阴影部分的面积=两个扇形面积和-2个空白区域面积的和=π-1.故选A.
模型分析 当所求阴影部分的图形比较复杂,难以通过构造和差进行计算时,常利用转化的方法将其转化为求扇形、三角形、特殊四边形的面积或它们面积的和差.
9.解析 (1)证明:如图,连接OC,
∵点C是的中点,∴,
∴∠ABC=∠EBC,
∵OB=OC,∴∠ABC=∠OCB,
∴∠EBC=∠OCB,∴OC∥BE,
∵BE⊥CE,∴半径OC⊥CE,∴CE是☉O的切线.
(2)如图,连接AC,
∵AB为☉O的直径,∴∠ACB=90°,∴∠ACB=∠CEB=90°,
又∵∠ABC=∠EBC,∴△ACB∽△CEB,
∴.
(3)如图,连接OD、CD,∵AB=4,∴OC=OB=2,
在Rt△BCE中,BC=2,BE=3,∴cos∠CBE=,
∴∠CBE=30°,∴∠COD=60°,∠ABC=30°,∴∠AOC=60°,
∵OC=OD,∠COD=60°,∴△COD是等边三角形,∴∠DCO=60°,
∴∠DCO=∠AOC,∴CD∥AB,∴S△COD=S△CBD,
∴S阴影=S扇形COD=π.
10.4π-8
解析 ∵AC是半圆O的切线,AB为半圆O的直径,∴∠CAB=90°,
∵点P是的中点,∴∠ABP=45°,∴∠C=45°,∴AB=AC=4,
∴阴影部分的面积=扇形CAD的面积+半圆O的面积-三角形ABC的面积=×4×4=4π-8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
专项素养综合全练(七)
与圆有关的阴影部分面积的计算
类型一 直接公式法
1.(2023山东郓城一中模拟)如图,在矩形ABCD中,AB=2BC=2,将线段AB绕点A按逆时针方向旋转,使得点B落在CD边上的点B'处,线段AB扫过部分(图中阴影部分)的面积为( )
A.
类型二 整体法
2.如图,以BC为直径的☉O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为 .(结果保留π)
类型三 和差法
考法一 直接和差法
模型分析
当所求阴影部分为不规则图形且图形相对比较简单时,阴影部分的面积可以直接看成扇形、三角形、特殊四边形的面积相加减.
3.(2023重庆中考B卷)如图,在矩形ABCD中,AB=2,BC=4,E为BC的中点,连接AE,DE.以E为圆心,EB长为半径画弧,分别与AE,DE交于点M,N.则图中阴影部分的面积为 .(结果保留π)
4.(2023湖北荆门外国语学校月考)如图,在矩形ABCD中,CD=2,以点C为圆心,CD长为半径画弧,交AB边于点E,且E为AB中点,则图中阴影部分的面积为 .
5.(2023山东济南历城二模改编)如图,在平面直角坐标系中,点A(-1,0),
B(1,0),C(0,1),将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A'处,得到△A'BC',则阴影部分的面积为 .
考法二 构造和差法
模型分析
常见 图形
添加辅 助线,构 造和差
阴影部 分面积 S阴影=S扇形OBD+ S△AOD S阴影=S扇形CA'A- S扇形CD'D
6.(2022贵州遵义中考)如图,在正方形ABCD中,AC和BD交于点O,过点O的直线EF交AB于点E(E不与A,B重合),交CD于点F.以点O为圆心,OC为半径的圆交直线EF于点M,N.若AB=1,则图中阴影部分的面积为( )
A.
7.(2023山东滨州中考)如图,某玩具品牌的标志由半径为1 cm的三个等圆构成,且三个等圆☉O1,☉O2,☉O3相互经过彼此的圆心,则图中三个阴影部分的面积之和为( )
A.π cm2 B.π cm2 C.π cm2 D.π cm2
类型四 转化法
模型分析
S阴影=S△BCE S阴影=(S☉O-S正方形ABCD) S阴影=S扇形OCD
对称转化 整体转化 等积转化
8.(2023山东济南槐荫一模)如图,两个半径长均为1的直角扇形的圆心分别在对方的圆弧上,扇形CFD的圆心C是弧AB的中点,且扇形CFD绕着点C旋转,半径AE、CF交于点G,半径BE、CD交于点H,则图中阴影部分的面积等于( )
A. C.π-1 D.π-2
9.(2023山东枣庄中考)如图,AB为☉O的直径,点C是的中点,过点C作射线BD的垂线,垂足为E.
(1)求证:CE是☉O的切线;
(2)若BE=3,AB=4,求BC的长;
(3)在(2)的条件下,求阴影部分的面积(用含有π的式子表示).
类型五 容斥原理法
模型分析
有的阴影部分面积是由两个基本图形相互重叠得到的.常用的方法是被重叠图形的面积=两个基本图形的面积之和-组合图形的面积.
如图,S阴影=S扇形CAE+S扇形CBD-S△ABC.
10.已知AB为半圆O的直径,且AB=4,点P是的中点.如图,过点A作半圆O的切线AC,与BP的延长线交于点C,以点C为圆心,AC长为半径画弧交BC于点D,则图中阴影部分的面积是 .
答案全解全析
1.B ∵AB=2BC=2,∴BC=1,
∵四边形ABCD是矩形,∴AD=BC=1,∠D=∠DAB=90°,
由旋转可得AB'=AB=2,∴cos∠DAB'=,∴∠DAB'=60°,
∴∠BAB'=30°,∴线段AB扫过部分的面积=,故选B.
2.π
解析 ∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵△OBD、△OCE是等腰三角形,
∴∠BDO+∠CEO=∠ABC+∠ACB=120°,
∴∠BOD+∠COE=360°-(∠BDO+∠CEO)-(∠ABC+∠ACB)=360°-120°-120°=120°,
∵BC=4,∴OB=OC=2,∴S阴影=π.
3.4-π
解析 ∵四边形ABCD为矩形,AB=2,
∴∠ABC=∠DCB=90°,CD=AB=2,
∵BC=4,E为BC的中点,
∴BE=CE=2,
∴AB=BE,CD=CE,
∴∠BAE=∠AEB=∠CDE=∠DEC=45°,
∴阴影部分的面积为2×=4-π.
4.
解析 ∵四边形ABCD为矩形,∴AB=CD=2,∠B=∠DCB=90°,
∵E为AB中点,∴EB=AB=1,
由作图可知CE=CD=2,∴∠ECB=30°,∴∠DCE=60°,
∵EB=1,CE=2,∴由勾股定理可知BC=,
∴阴影部分的面积=S矩形ABCD-S△CBE-S扇形ECD=.
5.
解析 ∵点A(-1,0),B(1,0),C(0,1),∴OA=OB=OC=1,
∴BC=,AB=2,
由旋转可知BA'=BA=2,
又OB=1,∴∠OA'B=30°,∴∠ABA'=90°-30°=60°=∠CBC',
∴S阴影=S扇形BAA'+S△BA'C'-S扇形BCC'-S△ABC =S扇形BAA'-S扇形BCC' = =.
6.B 如图,以O为圆心,OD为半径作弧DN,
易知OD=,S△OBE=S△ODF,S扇形BOM=S扇形DON,
∴S1=S2,∴S阴影=S扇形DOC-S△DOC=,故选B.
模型分析 当所求阴影部分为不规则图形,且图形相对比较复杂,不能直接看成规则图形的面积和差时,常通过“分割求和”“整体作差”等方法,添加适当的辅助线,构造扇形、三角形或特殊四边形,然后把它们的面积相加减.构造图形时一般先观察阴影部分图形:①若阴影部分图形有一部分是弧线,则需找出弧线所对应的圆心,连半径构造扇形;
②若阴影部分是由图形旋转而成的,则旋转中心即为圆心,将旋转前后的对应点分别与旋转中心连接构造扇形.
7.C 如图所示,连接O1A,O2A,O1B,O3B,O2C,O3C,O1O2,O1O3,O2O3,则△O1AO2,△O1BO3,△O2CO3,△O1O2O3是边长为1 cm的正三角形,所以S阴影=3(cm2),故选C.
8.A 两扇形的面积和为π,连接CE,过点C作CM⊥AE,作CN⊥BE,垂足分别为M、N,则四边形EMCN是矩形,∴∠MCN=
90°,∴∠MCG+∠FCN=90°,∵∠NCH+∠FCN=90°,∴∠MCG=∠NCH,∵点C是弧AB的中点,∴EC平分∠AEB,∴CM=CN,∴矩形EMCN是正方形,在△CMG与△CNH中,∴△CMG≌△CNH(ASA),∴图中空白区域面积等于对角线长是1的正方形面积,∴空白区域的面积为,
∴图中阴影部分的面积=两个扇形面积和-2个空白区域面积的和=π-1.故选A.
模型分析 当所求阴影部分的图形比较复杂,难以通过构造和差进行计算时,常利用转化的方法将其转化为求扇形、三角形、特殊四边形的面积或它们面积的和差.
9.解析 (1)证明:如图,连接OC,
∵点C是的中点,∴,
∴∠ABC=∠EBC,
∵OB=OC,∴∠ABC=∠OCB,
∴∠EBC=∠OCB,∴OC∥BE,
∵BE⊥CE,∴半径OC⊥CE,∴CE是☉O的切线.
(2)如图,连接AC,
∵AB为☉O的直径,∴∠ACB=90°,∴∠ACB=∠CEB=90°,
又∵∠ABC=∠EBC,∴△ACB∽△CEB,
∴.
(3)如图,连接OD、CD,∵AB=4,∴OC=OB=2,
在Rt△BCE中,BC=2,BE=3,∴cos∠CBE=,
∴∠CBE=30°,∴∠COD=60°,∠ABC=30°,∴∠AOC=60°,
∵OC=OD,∠COD=60°,∴△COD是等边三角形,∴∠DCO=60°,
∴∠DCO=∠AOC,∴CD∥AB,∴S△COD=S△CBD,
∴S阴影=S扇形COD=π.
10.4π-8
解析 ∵AC是半圆O的切线,AB为半圆O的直径,∴∠CAB=90°,
∵点P是的中点,∴∠ABP=45°,∴∠C=45°,∴AB=AC=4,
∴阴影部分的面积=扇形CAD的面积+半圆O的面积-三角形ABC的面积=×4×4=4π-8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
