2024北师大版数学九年级下学期课时练--专项素养综合全练(四)二次函数的图象信息题的四种常见类型(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--专项素养综合全练(四)二次函数的图象信息题的四种常见类型(含解析) | 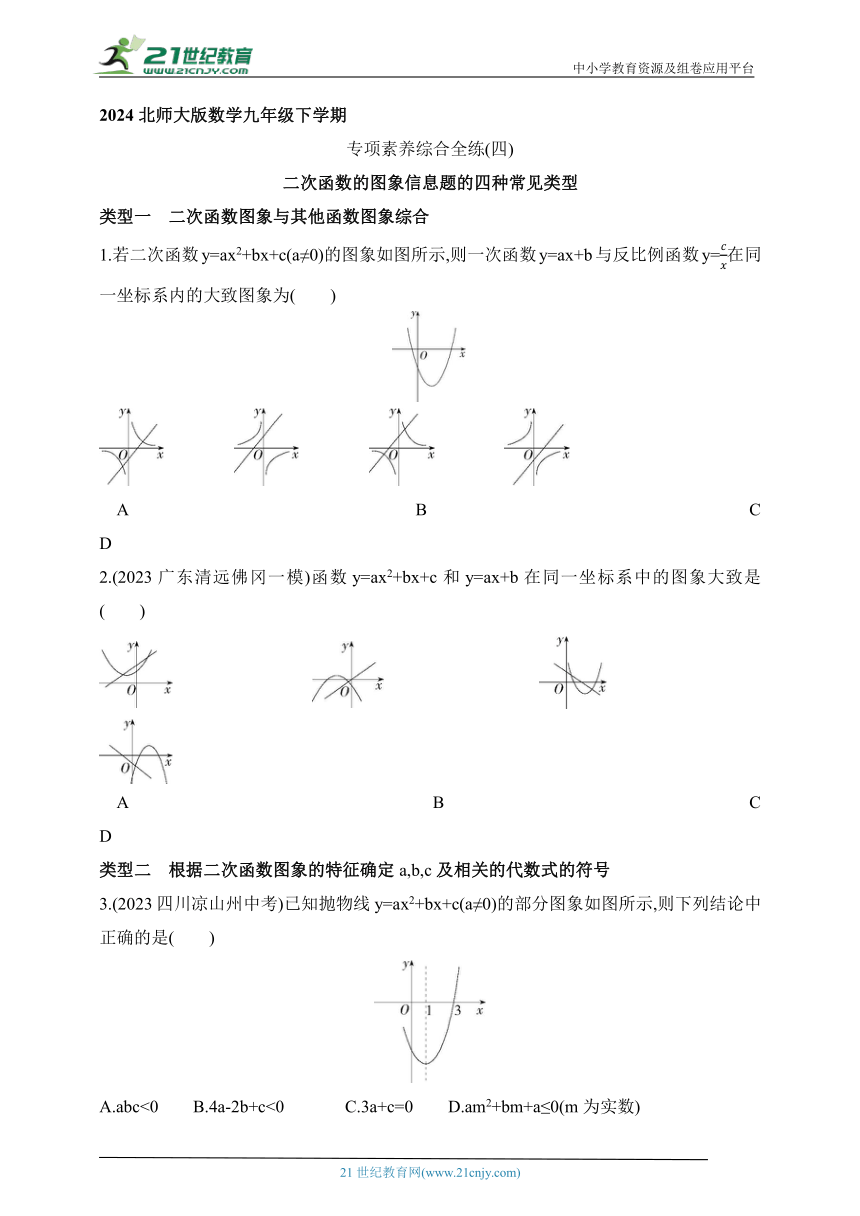 | |
| 格式 | docx | ||
| 文件大小 | 478.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 13:05:47 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
专项素养综合全练(四)
二次函数的图象信息题的四种常见类型
类型一 二次函数图象与其他函数图象综合
1.若二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一坐标系内的大致图象为( )
A B C D
2.(2023广东清远佛冈一模)函数y=ax2+bx+c和y=ax+b在同一坐标系中的图象大致是( )
A B C D
类型二 根据二次函数图象的特征确定a,b,c及相关的代数式的符号
3.(2023四川凉山州中考)已知抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,则下列结论中正确的是( )
A.abc<0 B.4a-2b+c<0 C.3a+c=0 D.am2+bm+a≤0(m为实数)
4.(2023山东莱西二模改编)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0;②b2<4ac;③若m为任意实数,则a+b>am2+bm;④a-b+c>0;⑤3a+c<0;⑥若a+bx2,且x1≠x2,则x1+x2=2.其中正确结论的个数为( )
A.2 B.3 C.4 D.5
类型三 利用二次函数的图象比较大小
5.二次函数y=ax2+bx+c的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )
A.y1C.y1>y2 D.不能确定
6.(2023安徽合肥三模)如图所示,在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴相交于不同的两点A、B,且该抛物线的顶点E在矩形ABCD的边CD上,AD=4.
(1)若点A的坐标为(1,0).
①求该抛物线的关系式;
②若点P(m,y1),Q(n,y2)都在此抛物线上,且-2≤m<-1,0(2)求边AB的长度.
类型四 利用二次函数的图象求方程的解或不等式的解集
7.(2023宁夏同心二模)在同一平面直角坐标系中,抛物线y1=-x2+4x和直线y2=2x如图所示,则不等式y1>y2的解集是( )
A.x<0 B.02 D.x>2
8.(2023江西抚州三模)如图,抛物线y=ax2+bx+c交x轴于(-1,0),(3,0)两点,则下列判断中,错误的是( )
A.图象的对称轴是直线x=1
B.当x>2时,y随x的增大而减小
C.若图象上两点为(-7,y1),(8,y2),则y1>y2
D.一元二次方程ax2+bx+c=0的两个根是-1和3
9.已知二次函数y=x2-2x-3.
(1)请你把已知的二次函数化成y=(x-h)2+k的形式: ,并在平面直角坐标系(如图)中画出它的图象;
(2)如果A(x1,y1),B(x2,y2)是(1)中图象上的两点,且x1(3)利用(1)中的图象表示出方程x2-2x-1=0的根m,n(m(4)观察(1)中的图象知,当x>0时,y的取值范围是 .
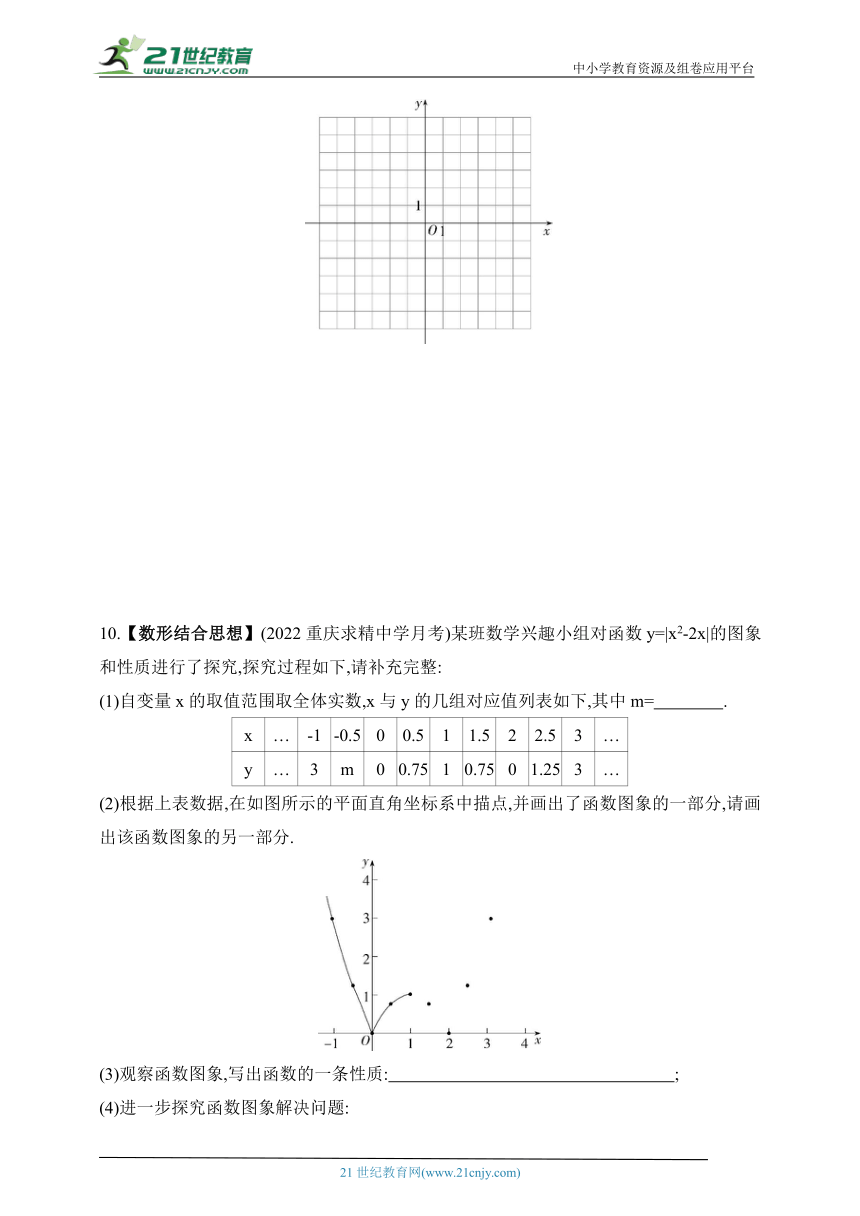
10.【数形结合思想】(2022重庆求精中学月考)某班数学兴趣小组对函数y=|x2-2x|的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围取全体实数,x与y的几组对应值列表如下,其中m= .
x … -1 -0.5 0 0.5 1 1.5 2 2.5 3 …
y … 3 m 0 0.75 1 0.75 0 1.25 3 …
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出函数的一条性质: ;
(4)进一步探究函数图象解决问题:
①方程|x2-2x|=有 个实数根;
②在图中画出直线y=-x+1,根据图象写出方程|x2-2x|=-x+1的一个正数根约为 .(精确到0.1)
答案全解全析
1.D ∵抛物线开口向上,∴a>0,∵抛物线的对称轴在y轴右侧,∴b<0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴直线y=ax+b经过第一、三、四象限,反比例函数y=的图象经过第二、四象限,故选D.
2.A B、C中,两函数图象反映的a的符号不相符,错误;当a>0,b>0时,直线过第一、二、三象限,抛物线开口向上且对称轴在y轴左侧,A正确;当a<0,b<0时,直线过第二、三、四象限,抛物线开口向下且对称轴在y轴左侧,D错误.故选A.
3.C 由抛物线开口向上知a>0,∵抛物线的对称轴为直线x=1,∴-=1,∴b=-2a,∴b<0,∵抛物线与y轴交于负半轴,∴c<0,∴abc>0,故A错误;∵抛物线的对称轴为直线x=1,且4-1=1-(-2),∴抛物线上的点(4,16a+
4b+c)与(-2,4a-2b+c)关于对称轴对称,由题图可知,点(4,16a+4b+c)在第一象限,∴点(-2,4a-2b+c)在第二象限,∴4a-2b+c>0,故B错误;∵x=3时,y=0,∴9a+3b+c=0,∵b=-2a,∴9a+3×(-2a)+c=0,∴3a+c=0,故C正确;∵b=-2a,∴am2+bm+a=am2-2am+a=a(m-1)2,∵a>0,(m-1)2≥0,∴a(m-1)2
≥0,∴am2+bm+a≥0,故D错误.故选C.
4.B ①∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=-=1,∴b=-2a>0,∴2a+b=0,故①正确;②∵抛物线与x轴有2个交点,∴b2-4ac>0,∴b2>4ac,故②错误;③∵抛物线的对称轴为直线x=1,∴函数的最大值为a+b+c,∴a+b+c≥am2+bm+c,即a+b≥am2+bm,故③错误;④∵抛物线与x轴的一个交点在(3,0)的左侧,对称轴为直线x=1,∴抛物线与x轴的另一个交点在(-1,0)的右侧,∴当x=-1时,y<0,∴a-b+c<0,故④错误;⑤∵b=-2a,a-b+c<0,∴a+2a+c<0,即3a+c<0,故⑤正确;⑥∵a-bx2=0,∴a(x1+x2)(x1-x2)+b(x1-x2)=0,∴(x1-x2)[a(x1+x2)+b]=0,∵x1≠x2,∴a(x1+x2)+b=0,即x1+x2=-,
∵b=-2a,∴x1+x2=2,故⑥正确.综上所述,正确的有①⑤⑥,共3个.
故选B.
5.C 观察图象可得,当x>-3时,y随x的增大而减小,∵1<2,∴y1>y2.故选C.
6.解析 (1)①∵AD=4,抛物线的顶点E在矩形ABCD的边CD上,
∴顶点的纵坐标为=4.
∵抛物线y=-x2+bx+c经过点A(1,0),
∴-1+b+c=0,即b=1-c,∴=4,解得c=-5(舍去)或c=3,
∴b=-2,∴抛物线的关系式为y=-x2-2x+3.
②y1>y2.理由如下:由①得抛物线的对称轴为直线x=-=-1,∵点P(m,y1),Q(n,y2)都在此抛物线上,且-2≤m<-1,01,∵a=-1<0,∴距离对称轴越远,函数值越小,∴y1>y2.
(2)∵AD=4,∴=4,
∵a=-1,∴b2+4c=16,
当y=0时,0=-x2+bx+c,
∴x=,
∴AB=xA-xB==4.
7.B ∵抛物线y1=-x2+4x和直线y2=2x交点的横坐标为0和2,
∴不等式-x2+4x>2x的解集为0即不等式y1>y2的解集为08.C 由图象可得,图象的对称轴是直线x==1,故选项A正确,不符合题意;当x>2时,y随x的增大而减小,故选项B正确,不符合题意;x=
-7和x=9对应的函数值相等,若图象上两点为(-7,y1),(8,y2),则y1故选C.
9.解析 (1)∵y=x2-2x-3=(x-1)2-4,
∴该抛物线的顶点坐标为(1,-4),对称轴为直线x=1.
当y=0时,x2-2x-3=0,解得x1=-1,x2=3,∴该抛物线与x轴的两个交点的坐标分别为(-1,0),(3,0);
当x=0时,y=-3,∴该抛物线与y轴的交点的坐标为(0,-3).
故答案为y=(x-1)2-4,画出该函数的图象如图所示.
(2)由(1)得,抛物线的对称轴是直线x=1,
∴当x<1时,y随x的增大而减小,
∵x1y2,故答案为y1>y2.
(3)当y=-2时,x2-2x-3=-2,∴x2-2x-1=0,
该方程的两个根即为抛物线y=x2-2x-3与直线y=-2的交点的横坐标,
如图,点M,N的横坐标即为m,n的值.
(4)由函数图象可知,当x>0时,函数图象的最低点为抛物线的顶点,
∴y的取值范围是y≥-4,故答案为y≥-4.
10.解析 (1)把x=-0.5代入y=|x2-2x|,得y=|(-0.5)2-2×(-0.5)|=1.25,
∴m=1.25.
(2)如图所示.
(3)当x>2时,y随x的增大而增大.答案不唯一.
(4)①由函数图象知,函数图象与直线y=有4个交点,所以方程|x2-2x|
=有4个实数根.
②画出直线y=-x+1如图,由图象和题表可知方程|x2-2x|=-x+1的一个正数根约为0.4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
专项素养综合全练(四)
二次函数的图象信息题的四种常见类型
类型一 二次函数图象与其他函数图象综合
1.若二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一坐标系内的大致图象为( )
A B C D
2.(2023广东清远佛冈一模)函数y=ax2+bx+c和y=ax+b在同一坐标系中的图象大致是( )
A B C D
类型二 根据二次函数图象的特征确定a,b,c及相关的代数式的符号
3.(2023四川凉山州中考)已知抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,则下列结论中正确的是( )
A.abc<0 B.4a-2b+c<0 C.3a+c=0 D.am2+bm+a≤0(m为实数)
4.(2023山东莱西二模改编)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0;②b2<4ac;③若m为任意实数,则a+b>am2+bm;④a-b+c>0;⑤3a+c<0;⑥若a+bx2,且x1≠x2,则x1+x2=2.其中正确结论的个数为( )
A.2 B.3 C.4 D.5
类型三 利用二次函数的图象比较大小
5.二次函数y=ax2+bx+c的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )
A.y1
6.(2023安徽合肥三模)如图所示,在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴相交于不同的两点A、B,且该抛物线的顶点E在矩形ABCD的边CD上,AD=4.
(1)若点A的坐标为(1,0).
①求该抛物线的关系式;
②若点P(m,y1),Q(n,y2)都在此抛物线上,且-2≤m<-1,0
类型四 利用二次函数的图象求方程的解或不等式的解集
7.(2023宁夏同心二模)在同一平面直角坐标系中,抛物线y1=-x2+4x和直线y2=2x如图所示,则不等式y1>y2的解集是( )
A.x<0 B.0
8.(2023江西抚州三模)如图,抛物线y=ax2+bx+c交x轴于(-1,0),(3,0)两点,则下列判断中,错误的是( )
A.图象的对称轴是直线x=1
B.当x>2时,y随x的增大而减小
C.若图象上两点为(-7,y1),(8,y2),则y1>y2
D.一元二次方程ax2+bx+c=0的两个根是-1和3
9.已知二次函数y=x2-2x-3.
(1)请你把已知的二次函数化成y=(x-h)2+k的形式: ,并在平面直角坐标系(如图)中画出它的图象;
(2)如果A(x1,y1),B(x2,y2)是(1)中图象上的两点,且x1
10.【数形结合思想】(2022重庆求精中学月考)某班数学兴趣小组对函数y=|x2-2x|的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围取全体实数,x与y的几组对应值列表如下,其中m= .
x … -1 -0.5 0 0.5 1 1.5 2 2.5 3 …
y … 3 m 0 0.75 1 0.75 0 1.25 3 …
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出函数的一条性质: ;
(4)进一步探究函数图象解决问题:
①方程|x2-2x|=有 个实数根;
②在图中画出直线y=-x+1,根据图象写出方程|x2-2x|=-x+1的一个正数根约为 .(精确到0.1)
答案全解全析
1.D ∵抛物线开口向上,∴a>0,∵抛物线的对称轴在y轴右侧,∴b<0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴直线y=ax+b经过第一、三、四象限,反比例函数y=的图象经过第二、四象限,故选D.
2.A B、C中,两函数图象反映的a的符号不相符,错误;当a>0,b>0时,直线过第一、二、三象限,抛物线开口向上且对称轴在y轴左侧,A正确;当a<0,b<0时,直线过第二、三、四象限,抛物线开口向下且对称轴在y轴左侧,D错误.故选A.
3.C 由抛物线开口向上知a>0,∵抛物线的对称轴为直线x=1,∴-=1,∴b=-2a,∴b<0,∵抛物线与y轴交于负半轴,∴c<0,∴abc>0,故A错误;∵抛物线的对称轴为直线x=1,且4-1=1-(-2),∴抛物线上的点(4,16a+
4b+c)与(-2,4a-2b+c)关于对称轴对称,由题图可知,点(4,16a+4b+c)在第一象限,∴点(-2,4a-2b+c)在第二象限,∴4a-2b+c>0,故B错误;∵x=3时,y=0,∴9a+3b+c=0,∵b=-2a,∴9a+3×(-2a)+c=0,∴3a+c=0,故C正确;∵b=-2a,∴am2+bm+a=am2-2am+a=a(m-1)2,∵a>0,(m-1)2≥0,∴a(m-1)2
≥0,∴am2+bm+a≥0,故D错误.故选C.
4.B ①∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=-=1,∴b=-2a>0,∴2a+b=0,故①正确;②∵抛物线与x轴有2个交点,∴b2-4ac>0,∴b2>4ac,故②错误;③∵抛物线的对称轴为直线x=1,∴函数的最大值为a+b+c,∴a+b+c≥am2+bm+c,即a+b≥am2+bm,故③错误;④∵抛物线与x轴的一个交点在(3,0)的左侧,对称轴为直线x=1,∴抛物线与x轴的另一个交点在(-1,0)的右侧,∴当x=-1时,y<0,∴a-b+c<0,故④错误;⑤∵b=-2a,a-b+c<0,∴a+2a+c<0,即3a+c<0,故⑤正确;⑥∵a-bx2=0,∴a(x1+x2)(x1-x2)+b(x1-x2)=0,∴(x1-x2)[a(x1+x2)+b]=0,∵x1≠x2,∴a(x1+x2)+b=0,即x1+x2=-,
∵b=-2a,∴x1+x2=2,故⑥正确.综上所述,正确的有①⑤⑥,共3个.
故选B.
5.C 观察图象可得,当x>-3时,y随x的增大而减小,∵1<2,∴y1>y2.故选C.
6.解析 (1)①∵AD=4,抛物线的顶点E在矩形ABCD的边CD上,
∴顶点的纵坐标为=4.
∵抛物线y=-x2+bx+c经过点A(1,0),
∴-1+b+c=0,即b=1-c,∴=4,解得c=-5(舍去)或c=3,
∴b=-2,∴抛物线的关系式为y=-x2-2x+3.
②y1>y2.理由如下:由①得抛物线的对称轴为直线x=-=-1,∵点P(m,y1),Q(n,y2)都在此抛物线上,且-2≤m<-1,0
(2)∵AD=4,∴=4,
∵a=-1,∴b2+4c=16,
当y=0时,0=-x2+bx+c,
∴x=,
∴AB=xA-xB==4.
7.B ∵抛物线y1=-x2+4x和直线y2=2x交点的横坐标为0和2,
∴不等式-x2+4x>2x的解集为0
-7和x=9对应的函数值相等,若图象上两点为(-7,y1),(8,y2),则y1
9.解析 (1)∵y=x2-2x-3=(x-1)2-4,
∴该抛物线的顶点坐标为(1,-4),对称轴为直线x=1.
当y=0时,x2-2x-3=0,解得x1=-1,x2=3,∴该抛物线与x轴的两个交点的坐标分别为(-1,0),(3,0);
当x=0时,y=-3,∴该抛物线与y轴的交点的坐标为(0,-3).
故答案为y=(x-1)2-4,画出该函数的图象如图所示.
(2)由(1)得,抛物线的对称轴是直线x=1,
∴当x<1时,y随x的增大而减小,
∵x1
(3)当y=-2时,x2-2x-3=-2,∴x2-2x-1=0,
该方程的两个根即为抛物线y=x2-2x-3与直线y=-2的交点的横坐标,
如图,点M,N的横坐标即为m,n的值.
(4)由函数图象可知,当x>0时,函数图象的最低点为抛物线的顶点,
∴y的取值范围是y≥-4,故答案为y≥-4.
10.解析 (1)把x=-0.5代入y=|x2-2x|,得y=|(-0.5)2-2×(-0.5)|=1.25,
∴m=1.25.
(2)如图所示.
(3)当x>2时,y随x的增大而增大.答案不唯一.
(4)①由函数图象知,函数图象与直线y=有4个交点,所以方程|x2-2x|
=有4个实数根.
②画出直线y=-x+1如图,由图象和题表可知方程|x2-2x|=-x+1的一个正数根约为0.4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
