2024北师大版数学九年级下学期课时练--专项素养综合全练(五)二次函数与几何图形的综合(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--专项素养综合全练(五)二次函数与几何图形的综合(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 490.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
专项素养综合全练(五)
二次函数与几何图形的综合
类型一 线段最值问题
1.(2023安徽合肥五十中期末)如图,抛物线y=-x2+bx+c与x轴交于A(-2,0),B(8,0)两点,与y轴交于点C.点P是第一象限内抛物线上的一个动点,过点P作直线PD⊥x轴于点D,交直线BC于点E.
(1)求抛物线的解析式;
(2)求线段PE长度的最大值.
类型二 面积问题
2.(2023四川泸州中考)如图,在平面直角坐标系xOy中,已知抛物线y=ax2+2x+c与坐标轴分别相交于A,B,C(0,6)三点,其对称轴为直线x=2.
(1)求该抛物线的解析式.
(2)点F是该抛物线上位于第一象限的一个动点,直线AF分别与y轴,直线BC交于点D,E.
①当CD=CE时,求CD的长;
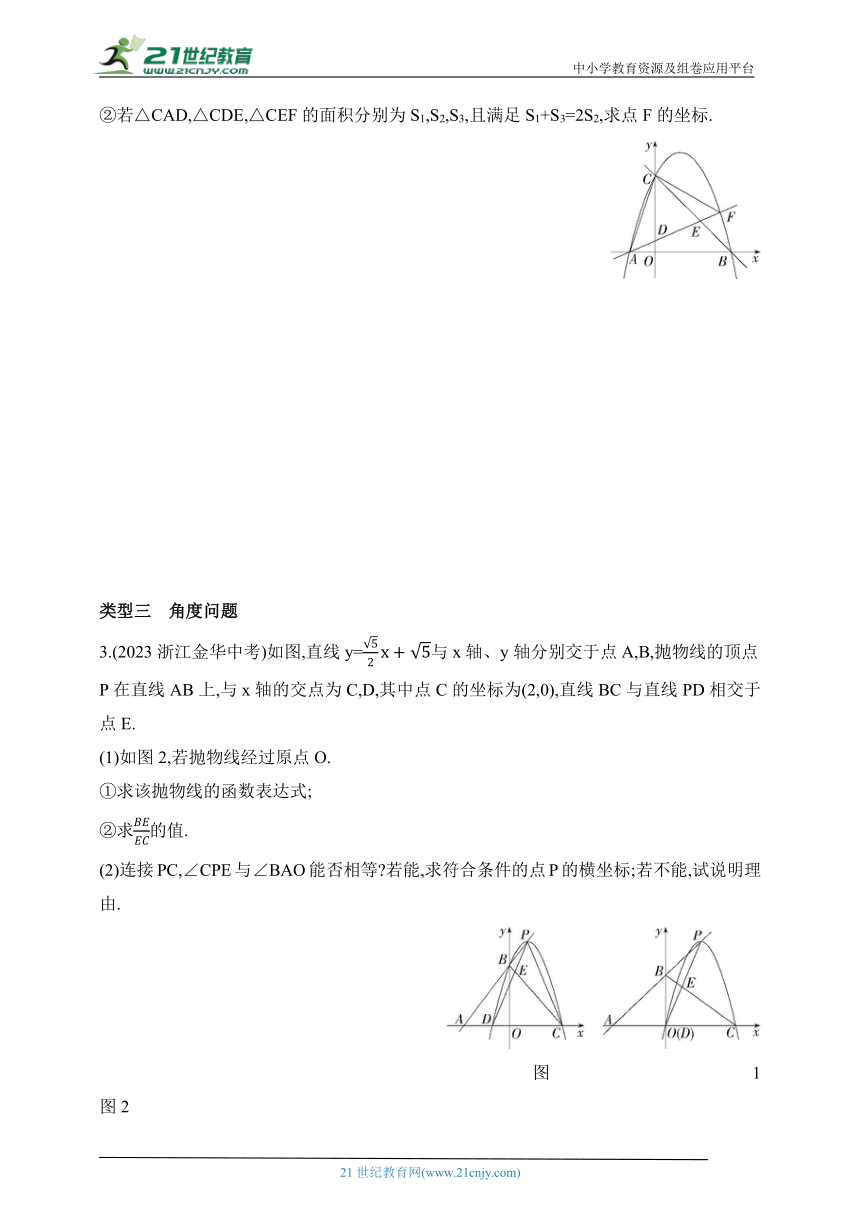
②若△CAD,△CDE,△CEF的面积分别为S1,S2,S3,且满足S1+S3=2S2,求点F的坐标.
类型三 角度问题
3.(2023浙江金华中考)如图,直线y=与x轴、y轴分别交于点A,B,抛物线的顶点P在直线AB上,与x轴的交点为C,D,其中点C的坐标为(2,0),直线BC与直线PD相交于点E.
(1)如图2,若抛物线经过原点O.
①求该抛物线的函数表达式;
②求的值.
(2)连接PC,∠CPE与∠BAO能否相等 若能,求符合条件的点P的横坐标;若不能,试说明理由.
图1 图2
类型四 特殊三角形存在性问题
4.(2023重庆中考B卷)如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A,B,与y轴交于点C,其中B(3,0),C(0,-3).
(1)求该抛物线的表达式;
(2)点P是直线AC下方抛物线上一动点,过点P作PD⊥AC于点D,求PD的最大值及此时点P的坐标;
(3)在(2)的条件下,将该抛物线向右平移5个单位,点E为点P的对应点,平移后的抛物线与y轴交于点F,Q为平移后的抛物线的对称轴上任意一点,写出所有使得以QF为腰的△QEF是等腰三角形的点Q的坐标,并把求其中一个点Q的坐标的过程写出来.
备用图
类型五 特殊四边形存在性问题
5.(2023四川达州中考)如图,抛物线y=ax2+bx+c过点A(-1,0),B(3,0),
C(0,3).
(1)求抛物线的解析式.
(2)设点P是直线BC上方抛物线上一点,求出△PBC的最大面积及此时点P的坐标.
(3)若点M是抛物线对称轴上一动点,点N为坐标平面内一点,是否存在以BC为边,点B、C、M、N为顶点的四边形是菱形 若存在,请直接写出点N的坐标;若不存在,请说明理由.
备用图
类型六 相似三角形判定问题
6.(2023湖北随州中考)如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(-1,0),B(2,0)和C(0,2),点P(m,n)(m>0)为抛物线上一动点,过点P作PN⊥x轴交直线BC于点M,交x轴于点N.
(1)直接写出抛物线和直线BC的解析式.
(2)如图2,连接OM,当△OCM为等腰三角形时,求m的值.
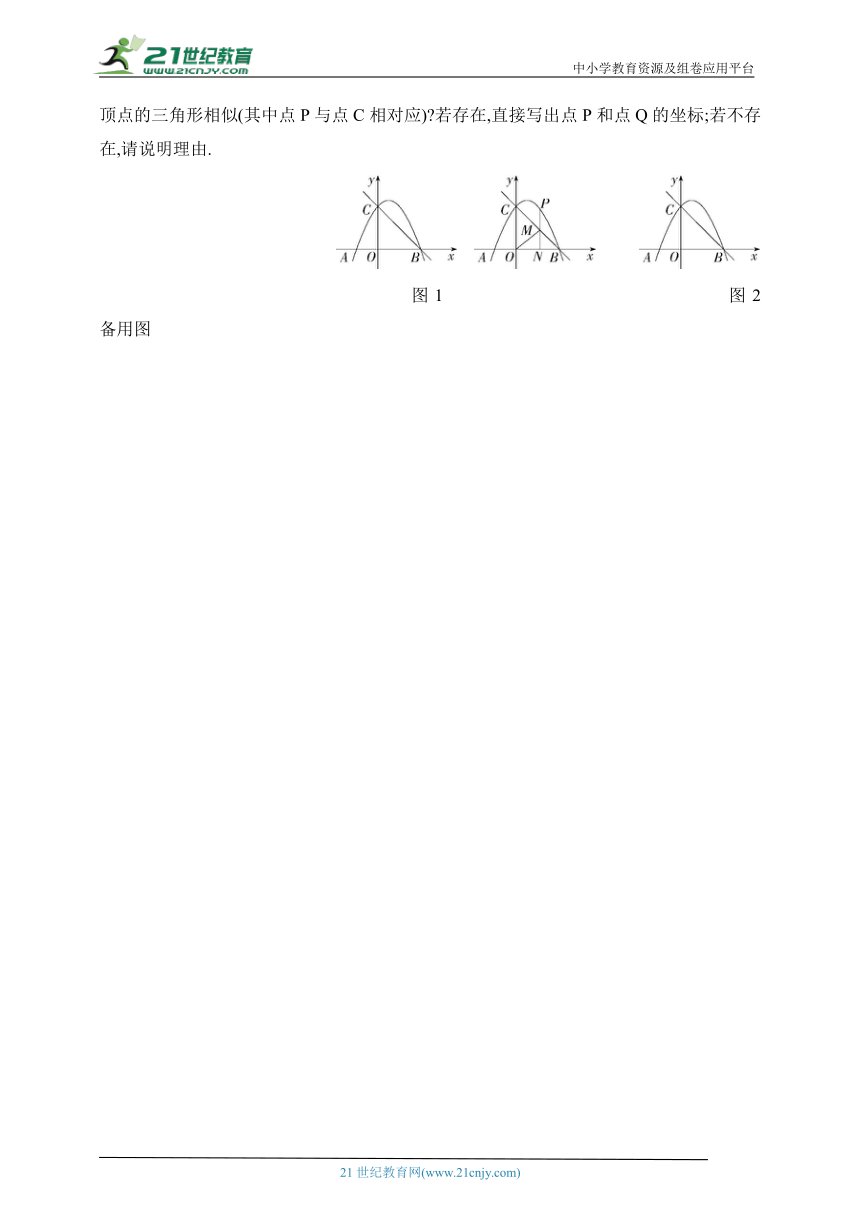
(3)P点在运动过程中,在y轴上是否存在点Q,使得以O,P,Q为顶点的三角形与以B,C,N为顶点的三角形相似(其中点P与点C相对应) 若存在,直接写出点P和点Q的坐标;若不存在,请说明理由.
图1 图2 备用图
答案全解全析
1.解析 (1)将A(-2,0),B(8,0)代入y=-x2+bx+c中,可得
即抛物线的解析式为y=-x+4.
(2)当x=0时,y=-x+4=4,∴C(0,4),
设BC的解析式为y=kx+n,
将B(8,0),C(0,4)代入,得
解得
即BC的解析式为y=-x+4,
∵直线PD⊥x轴,
∴点P、E的横坐标相等,设为m,0∴E,
∴PE=(m-4)2+4,
∵02.解析 (1)由题意得
∴抛物线的解析式为y=-x2+2x+6.
(2)令y=0,则-x2+2x+6=0,解得x=6或x=-2,
∴点A,B的坐标分别为(-2,0),(6,0).
①设点F,
由点A,F的坐标得,直线AF的表达式为y=-(m-6)(x+2),
当x=0时,y=-(m-6)(x+2)=6-m,即点D(0,6-m),则CD=6-6+m=m,
由点B,C的坐标得,直线BC的表达式为y=-x+6,
联立得则点E,
由点C,E的坐标得CE=
,解得m=0(舍去)或8-2,则CD=m=8-2.
②过点E,F分别作x轴的垂线,垂足分别为点M,N,
∵△CAD,△CDE,△CEF同高,
∴其面积比为底边的比,∴=2,
∵OD∥EM∥FN,∴,
∴=2,
∴=2,整理得3xE-xF=2,
由①知xE=,xF=m,
则3×-m=2,解得m=4(舍去负值),
经检验,m=4是分式方程的根,则点F(4,6).
3.解析 (1)①∵抛物线经过原点O(0,0),C(2,0),
∴其对称轴为直线x=1,当x=1时,y=,
∴抛物线的顶点P的坐标为,
设抛物线的解析式为y=a(x-1)2+,
把C(2,0)代入,得a+=0,解得a=-
x,
∴该抛物线的函数表达式为y=-x.
②∵直线y=与x轴、y轴分别交于点A,B,
∴A(-2,0),B(0,),
设直线OP的解析式为y=kx,
把P代入,得k=,
∴直线OP的解析式为y=x,
如图a,过点B作BF∥x轴交OP于点F,
则点F的纵坐标与点B的纵坐标相同,∴点F的纵坐标为,
在y=x中,令y=,则x,解得x=,
∵BF∥OC,∴△BEF∽△CEO,∴.
图a 图b
(2)能.如图b,过点P作PF⊥x轴于点F,设P,则F(m,0),∴PF=,AF=m-(-2)=m+2,AC=2-(-2)=4,
在Rt△APF中,AP2=AF2+PF2=(m+2)2+m2+9m+9,
若∠CPE=∠BAO,
∵∠PCD=∠ACP,∴△CPD∽△CAP,∴∠CDP=∠CPA,
∵PC=PD,∴∠CDP=∠ACP,∴∠PCD=∠CPA,∴AP=AC,
∴m2+9m+9=16,解得m1=-(舍去),m2=,
∴∠CPE与∠BAO能相等,点P的横坐标为.
4.解析 (1)由题意得
则抛物线的表达式为y=x-3.
(2)在y=x-3中,令y=0,
则x-3=0,解得x=-4或3,则点A(-4,0),
由点A、C知,直线AC的表达式为y=-x-3,
过点P作y轴的平行线交AC于点H,
则∠PHC=∠ACO,则tan∠PHC=tan∠ACO=,
易求得sin∠PHC=,则PD=PH·sin∠PHC=PH,
设点H,则点P(n,n-3),
则PD=(-n+3)=-,
当n=-2时,PD的长取得最大值,最大值为,此时点P.
(3)由题意可知点E的坐标为,即.
平移后的抛物线的表达式为y=(x-5)-3,
即y=x+2,
则点F(0,2),抛物线的对称轴为直线x=,
设点Q,则QF2=,
当QE=QF时,,解得m=,则点Q的坐标为;
当QF=EF时,,解得m=5或-1,则点Q的坐标为.
综上,点Q的坐标为.
5.解析 (1)由题意,可设抛物线的表达式为y=a(x+1)(x-3)=a(x2-2x-3),
则-3a=3,解得a=-1,
故抛物线的表达式为y=-x2+2x+3.
(2)由点B、C的坐标得,直线BC的表达式为y=-x+3,
过点P作y轴的平行线交CB于点H,连接PC,PB.
设点P(m,-m2+2m+3),则点H(m,-m+3),
则△PBC的面积=S△PHC+S△PHB=PH·xP+PH·(xB-xP)=PH·xB
=PH·OB=,
∴△PBC的面积的最大值为,此时点P.
(3)存在.由题意可知,抛物线的对称轴为直线x=1,
设点M(1,t),N(x,y),
若BC为菱形BCMN的边,
则BC2=CM2,即32+32=12+(t-3)2,
解得t1=+3,
∵);
若BC为菱形BCNM的边,
则BC2=BM2,即32+32=(3-1)2+t2,
解得t3=,
∵
∴N3(-2,+3).
综上,点N的坐标为(4,-)或(4,)或(-2,+3)或(-2,-+3).
6.解析 (1)∵抛物线y=ax2+bx+c过点A(-1,0),B(2,0),
∴抛物线的解析式为y=a(x+1)(x-2),将点C(0,2)代入得2=-2a,
∴a=-1,∴抛物线的解析式为y=-(x+1)(x-2),即y=-x2+x+2.
设直线BC的解析式为y=kx+t,将B(2,0),C(0,2)代入得∴直线BC的解析式为y=-x+2.
(2)∵点M在直线BC上,且P(m,n),∴点M的坐标为(m,-m+2),
又C(0,2),O(0,0),
∴OC=2,CM2=(m-0)2+(-m+2-2)2=2m2,OM2=m2+(-m+2)2=2m2-4m+4.
当△OCM为等腰三角形时,
①若CM=OM,则CM2=OM2,即2m2=2m2-4m+4,解得m=1;
②若CM=OC,则CM2=OC2,即2m2=4,解得m=或m=-(舍去);
③若OM=OC,则OM2=OC2,即2m2-4m+4=4,解得m=2或m=0(舍去).综上,m=1或m=或m=2.
(3)存在.∵点P与点C相对应,∴△POQ∽△CBN或△POQ∽△CNB.①若点P在点B的左侧,则∠CBN=45°,BN=2-m,CB=2,
当△POQ∽△CBN,即∠POQ=45°时,直线OP的表达式为y=x,
∴-m2+m+2=m,解得m=或m=-(舍去),∴P(
)2=4,即OP=2,
∵,解得OQ=-1).
当△POQ∽△CNB,即∠PQO=45°时,
PQ=m,OQ=-m2+m+2+m=-m2+2m+2或OQ=m-(-m2+m+2)=m2-2,
∵,
解得m=1±(舍去)或,解得m=(负值舍去),
∴P.
②若点P在点B的右侧,则∠CBN=135°,BN=m-2,
当△POQ∽△CBN,即∠POQ=135°时,直线OP的表达式为y=-x,
∴-m2+m+2=-m,解得m=1+或m=1-(舍去),
∴P(1+
,解得OQ=1,∴Q(0,1).
当△POQ∽△CNB,即∠PQO=135°时,
PQ=
,解得m=1+或m=1-(舍去),
∴P(1+),Q(0,-2).
综上,P(-1)或P(),Q或P(1+),Q(0,1)或P(1+),Q(0,-2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
专项素养综合全练(五)
二次函数与几何图形的综合
类型一 线段最值问题
1.(2023安徽合肥五十中期末)如图,抛物线y=-x2+bx+c与x轴交于A(-2,0),B(8,0)两点,与y轴交于点C.点P是第一象限内抛物线上的一个动点,过点P作直线PD⊥x轴于点D,交直线BC于点E.
(1)求抛物线的解析式;
(2)求线段PE长度的最大值.
类型二 面积问题
2.(2023四川泸州中考)如图,在平面直角坐标系xOy中,已知抛物线y=ax2+2x+c与坐标轴分别相交于A,B,C(0,6)三点,其对称轴为直线x=2.
(1)求该抛物线的解析式.
(2)点F是该抛物线上位于第一象限的一个动点,直线AF分别与y轴,直线BC交于点D,E.
①当CD=CE时,求CD的长;
②若△CAD,△CDE,△CEF的面积分别为S1,S2,S3,且满足S1+S3=2S2,求点F的坐标.
类型三 角度问题
3.(2023浙江金华中考)如图,直线y=与x轴、y轴分别交于点A,B,抛物线的顶点P在直线AB上,与x轴的交点为C,D,其中点C的坐标为(2,0),直线BC与直线PD相交于点E.
(1)如图2,若抛物线经过原点O.
①求该抛物线的函数表达式;
②求的值.
(2)连接PC,∠CPE与∠BAO能否相等 若能,求符合条件的点P的横坐标;若不能,试说明理由.
图1 图2
类型四 特殊三角形存在性问题
4.(2023重庆中考B卷)如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A,B,与y轴交于点C,其中B(3,0),C(0,-3).
(1)求该抛物线的表达式;
(2)点P是直线AC下方抛物线上一动点,过点P作PD⊥AC于点D,求PD的最大值及此时点P的坐标;
(3)在(2)的条件下,将该抛物线向右平移5个单位,点E为点P的对应点,平移后的抛物线与y轴交于点F,Q为平移后的抛物线的对称轴上任意一点,写出所有使得以QF为腰的△QEF是等腰三角形的点Q的坐标,并把求其中一个点Q的坐标的过程写出来.
备用图
类型五 特殊四边形存在性问题
5.(2023四川达州中考)如图,抛物线y=ax2+bx+c过点A(-1,0),B(3,0),
C(0,3).
(1)求抛物线的解析式.
(2)设点P是直线BC上方抛物线上一点,求出△PBC的最大面积及此时点P的坐标.
(3)若点M是抛物线对称轴上一动点,点N为坐标平面内一点,是否存在以BC为边,点B、C、M、N为顶点的四边形是菱形 若存在,请直接写出点N的坐标;若不存在,请说明理由.
备用图
类型六 相似三角形判定问题
6.(2023湖北随州中考)如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(-1,0),B(2,0)和C(0,2),点P(m,n)(m>0)为抛物线上一动点,过点P作PN⊥x轴交直线BC于点M,交x轴于点N.
(1)直接写出抛物线和直线BC的解析式.
(2)如图2,连接OM,当△OCM为等腰三角形时,求m的值.
(3)P点在运动过程中,在y轴上是否存在点Q,使得以O,P,Q为顶点的三角形与以B,C,N为顶点的三角形相似(其中点P与点C相对应) 若存在,直接写出点P和点Q的坐标;若不存在,请说明理由.
图1 图2 备用图
答案全解全析
1.解析 (1)将A(-2,0),B(8,0)代入y=-x2+bx+c中,可得
即抛物线的解析式为y=-x+4.
(2)当x=0时,y=-x+4=4,∴C(0,4),
设BC的解析式为y=kx+n,
将B(8,0),C(0,4)代入,得
解得
即BC的解析式为y=-x+4,
∵直线PD⊥x轴,
∴点P、E的横坐标相等,设为m,0
∴PE=(m-4)2+4,
∵0
∴抛物线的解析式为y=-x2+2x+6.
(2)令y=0,则-x2+2x+6=0,解得x=6或x=-2,
∴点A,B的坐标分别为(-2,0),(6,0).
①设点F,
由点A,F的坐标得,直线AF的表达式为y=-(m-6)(x+2),
当x=0时,y=-(m-6)(x+2)=6-m,即点D(0,6-m),则CD=6-6+m=m,
由点B,C的坐标得,直线BC的表达式为y=-x+6,
联立得则点E,
由点C,E的坐标得CE=
,解得m=0(舍去)或8-2,则CD=m=8-2.
②过点E,F分别作x轴的垂线,垂足分别为点M,N,
∵△CAD,△CDE,△CEF同高,
∴其面积比为底边的比,∴=2,
∵OD∥EM∥FN,∴,
∴=2,
∴=2,整理得3xE-xF=2,
由①知xE=,xF=m,
则3×-m=2,解得m=4(舍去负值),
经检验,m=4是分式方程的根,则点F(4,6).
3.解析 (1)①∵抛物线经过原点O(0,0),C(2,0),
∴其对称轴为直线x=1,当x=1时,y=,
∴抛物线的顶点P的坐标为,
设抛物线的解析式为y=a(x-1)2+,
把C(2,0)代入,得a+=0,解得a=-
x,
∴该抛物线的函数表达式为y=-x.
②∵直线y=与x轴、y轴分别交于点A,B,
∴A(-2,0),B(0,),
设直线OP的解析式为y=kx,
把P代入,得k=,
∴直线OP的解析式为y=x,
如图a,过点B作BF∥x轴交OP于点F,
则点F的纵坐标与点B的纵坐标相同,∴点F的纵坐标为,
在y=x中,令y=,则x,解得x=,
∵BF∥OC,∴△BEF∽△CEO,∴.
图a 图b
(2)能.如图b,过点P作PF⊥x轴于点F,设P,则F(m,0),∴PF=,AF=m-(-2)=m+2,AC=2-(-2)=4,
在Rt△APF中,AP2=AF2+PF2=(m+2)2+m2+9m+9,
若∠CPE=∠BAO,
∵∠PCD=∠ACP,∴△CPD∽△CAP,∴∠CDP=∠CPA,
∵PC=PD,∴∠CDP=∠ACP,∴∠PCD=∠CPA,∴AP=AC,
∴m2+9m+9=16,解得m1=-(舍去),m2=,
∴∠CPE与∠BAO能相等,点P的横坐标为.
4.解析 (1)由题意得
则抛物线的表达式为y=x-3.
(2)在y=x-3中,令y=0,
则x-3=0,解得x=-4或3,则点A(-4,0),
由点A、C知,直线AC的表达式为y=-x-3,
过点P作y轴的平行线交AC于点H,
则∠PHC=∠ACO,则tan∠PHC=tan∠ACO=,
易求得sin∠PHC=,则PD=PH·sin∠PHC=PH,
设点H,则点P(n,n-3),
则PD=(-n+3)=-,
当n=-2时,PD的长取得最大值,最大值为,此时点P.
(3)由题意可知点E的坐标为,即.
平移后的抛物线的表达式为y=(x-5)-3,
即y=x+2,
则点F(0,2),抛物线的对称轴为直线x=,
设点Q,则QF2=,
当QE=QF时,,解得m=,则点Q的坐标为;
当QF=EF时,,解得m=5或-1,则点Q的坐标为.
综上,点Q的坐标为.
5.解析 (1)由题意,可设抛物线的表达式为y=a(x+1)(x-3)=a(x2-2x-3),
则-3a=3,解得a=-1,
故抛物线的表达式为y=-x2+2x+3.
(2)由点B、C的坐标得,直线BC的表达式为y=-x+3,
过点P作y轴的平行线交CB于点H,连接PC,PB.
设点P(m,-m2+2m+3),则点H(m,-m+3),
则△PBC的面积=S△PHC+S△PHB=PH·xP+PH·(xB-xP)=PH·xB
=PH·OB=,
∴△PBC的面积的最大值为,此时点P.
(3)存在.由题意可知,抛物线的对称轴为直线x=1,
设点M(1,t),N(x,y),
若BC为菱形BCMN的边,
则BC2=CM2,即32+32=12+(t-3)2,
解得t1=+3,
∵);
若BC为菱形BCNM的边,
则BC2=BM2,即32+32=(3-1)2+t2,
解得t3=,
∵
∴N3(-2,+3).
综上,点N的坐标为(4,-)或(4,)或(-2,+3)或(-2,-+3).
6.解析 (1)∵抛物线y=ax2+bx+c过点A(-1,0),B(2,0),
∴抛物线的解析式为y=a(x+1)(x-2),将点C(0,2)代入得2=-2a,
∴a=-1,∴抛物线的解析式为y=-(x+1)(x-2),即y=-x2+x+2.
设直线BC的解析式为y=kx+t,将B(2,0),C(0,2)代入得∴直线BC的解析式为y=-x+2.
(2)∵点M在直线BC上,且P(m,n),∴点M的坐标为(m,-m+2),
又C(0,2),O(0,0),
∴OC=2,CM2=(m-0)2+(-m+2-2)2=2m2,OM2=m2+(-m+2)2=2m2-4m+4.
当△OCM为等腰三角形时,
①若CM=OM,则CM2=OM2,即2m2=2m2-4m+4,解得m=1;
②若CM=OC,则CM2=OC2,即2m2=4,解得m=或m=-(舍去);
③若OM=OC,则OM2=OC2,即2m2-4m+4=4,解得m=2或m=0(舍去).综上,m=1或m=或m=2.
(3)存在.∵点P与点C相对应,∴△POQ∽△CBN或△POQ∽△CNB.①若点P在点B的左侧,则∠CBN=45°,BN=2-m,CB=2,
当△POQ∽△CBN,即∠POQ=45°时,直线OP的表达式为y=x,
∴-m2+m+2=m,解得m=或m=-(舍去),∴P(
)2=4,即OP=2,
∵,解得OQ=-1).
当△POQ∽△CNB,即∠PQO=45°时,
PQ=m,OQ=-m2+m+2+m=-m2+2m+2或OQ=m-(-m2+m+2)=m2-2,
∵,
解得m=1±(舍去)或,解得m=(负值舍去),
∴P.
②若点P在点B的右侧,则∠CBN=135°,BN=m-2,
当△POQ∽△CBN,即∠POQ=135°时,直线OP的表达式为y=-x,
∴-m2+m+2=-m,解得m=1+或m=1-(舍去),
∴P(1+
,解得OQ=1,∴Q(0,1).
当△POQ∽△CNB,即∠PQO=135°时,
PQ=
,解得m=1+或m=1-(舍去),
∴P(1+),Q(0,-2).
综上,P(-1)或P(),Q或P(1+),Q(0,1)或P(1+),Q(0,-2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
