2024北师大版数学九年级下学期课时练--1.1 锐角三角函数(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--1.1 锐角三角函数(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 14:05:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
第一章 直角三角形的边角关系
1 锐角三角函数
基础过关全练
知识点1 正切
1.(2023陕西西安高级中学初中部四模)如图,在Rt△ABC中,∠C=90°,AC=2,AB=3,则tan B的值为( )
A.
2.(2023浙江衢州实验学校月考)如图,点A(2,t)在第一象限,OA与x轴所夹的锐角为α,tan α=,则t的值是 .
3.【教材变式·P4随堂练习T1】如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=10,tan B=,求BC的长.
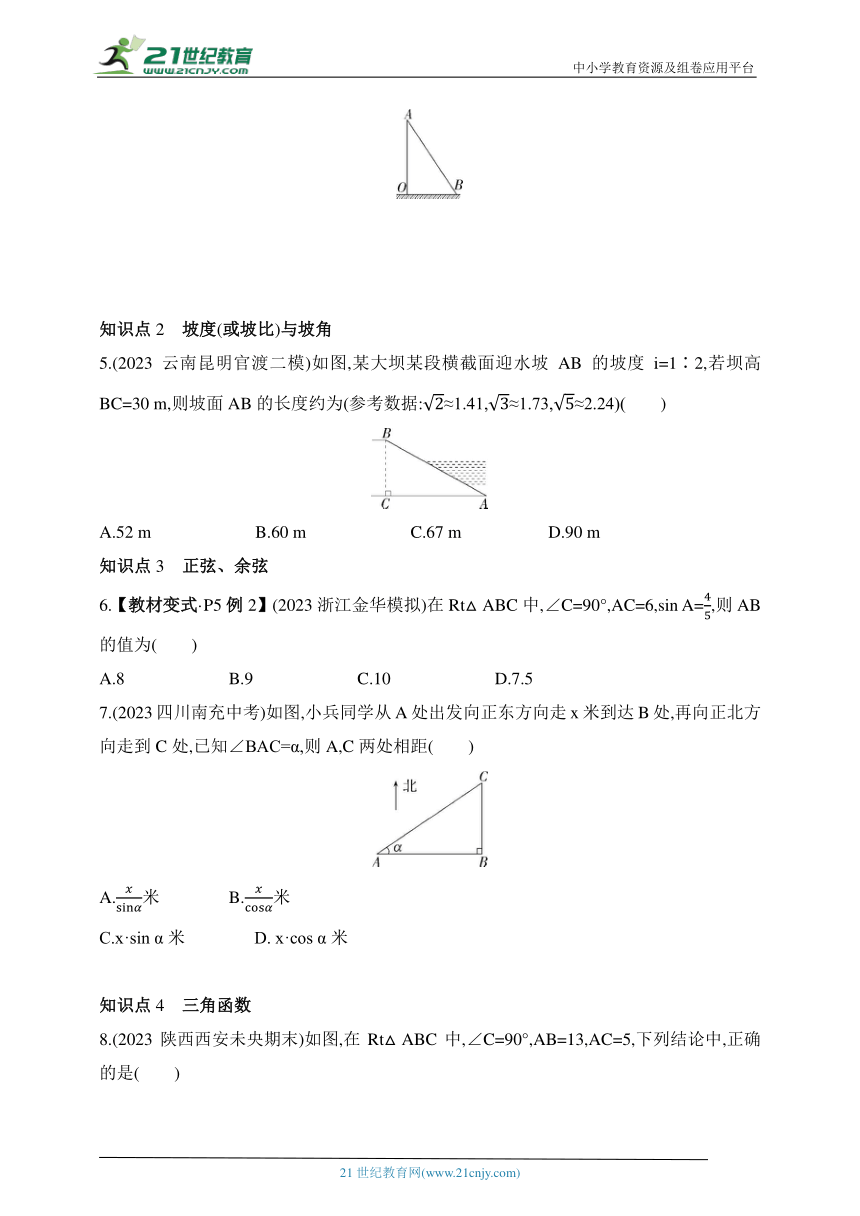
4.【新独家原创】小明放风筝时风筝线断了,风筝挂在了树上A处(如图),他先拉住风筝线垂直到地面上,发现风筝线多出2 m,然后把风筝线沿直线向右拉6 m,发现风筝线末端B刚好接触地面,请你求出这时∠ABO的正切值.
知识点2 坡度(或坡比)与坡角
5.(2023云南昆明官渡二模)如图,某大坝某段横截面迎水坡AB的坡度i=1∶2,若坝高BC=30 m,则坡面AB的长度约为(参考数据:≈1.41,≈1.73,≈2.24)( )
A.52 m B.60 m C.67 m D.90 m
知识点3 正弦、余弦
6.【教材变式·P5例2】(2023浙江金华模拟)在Rt△ABC中,∠C=90°,AC=6,sin A=,则AB的值为( )
A.8 B.9 C.10 D.7.5
7.(2023四川南充中考)如图,小兵同学从A处出发向正东方向走x米到达B处,再向正北方向走到C处,已知∠BAC=α,则A,C两处相距( )
A.米 B.米
C.x·sin α米 D. x·cos α米
知识点4 三角函数
8.(2023陕西西安未央期末)如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,下列结论中,正确的是( )
A.tan B= B.tan A=
C.sin A= D.cos B=
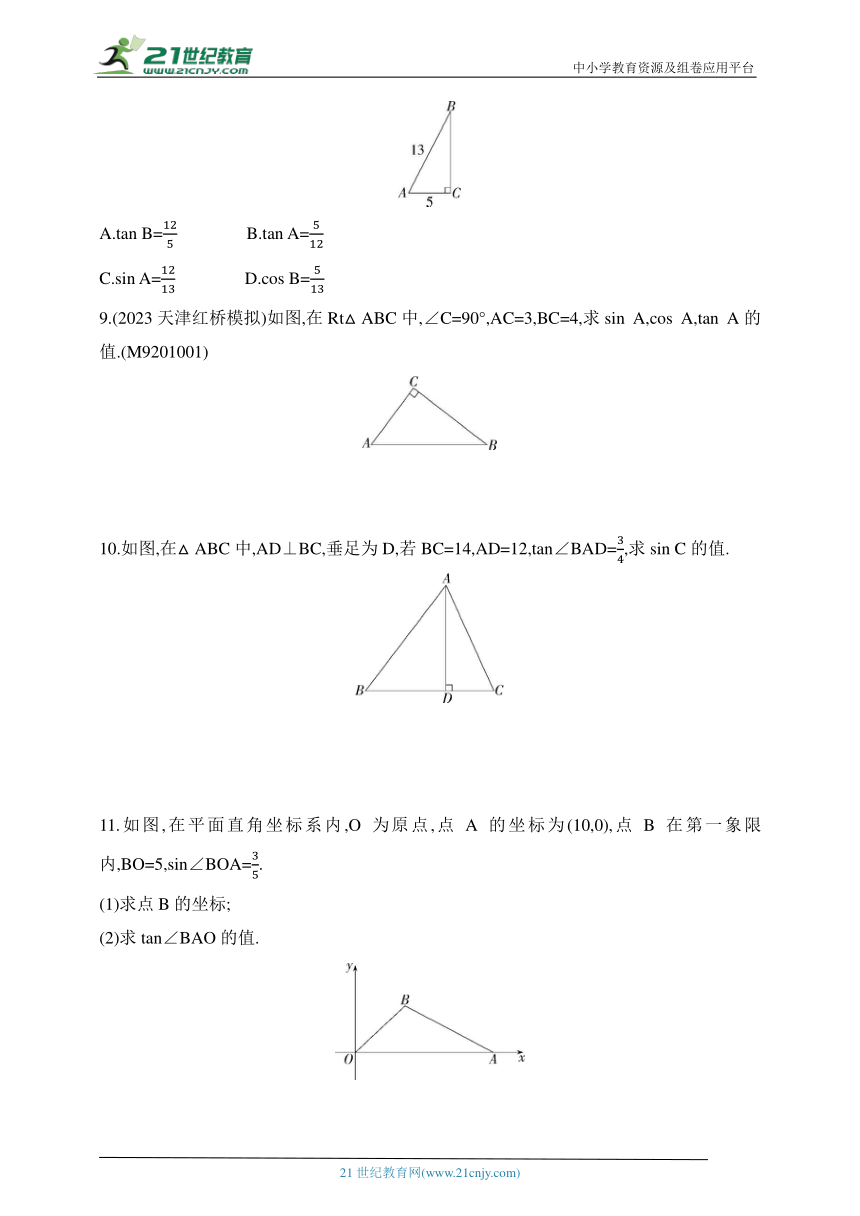
9.(2023天津红桥模拟)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,求sin A,cos A,tan A的值.(M9201001)
10.如图,在△ABC中,AD⊥BC,垂足为D,若BC=14,AD=12,tan∠BAD=,求sin C的值.
11.如图,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.
(1)求点B的坐标;
(2)求tan∠BAO的值.
能力提升全练
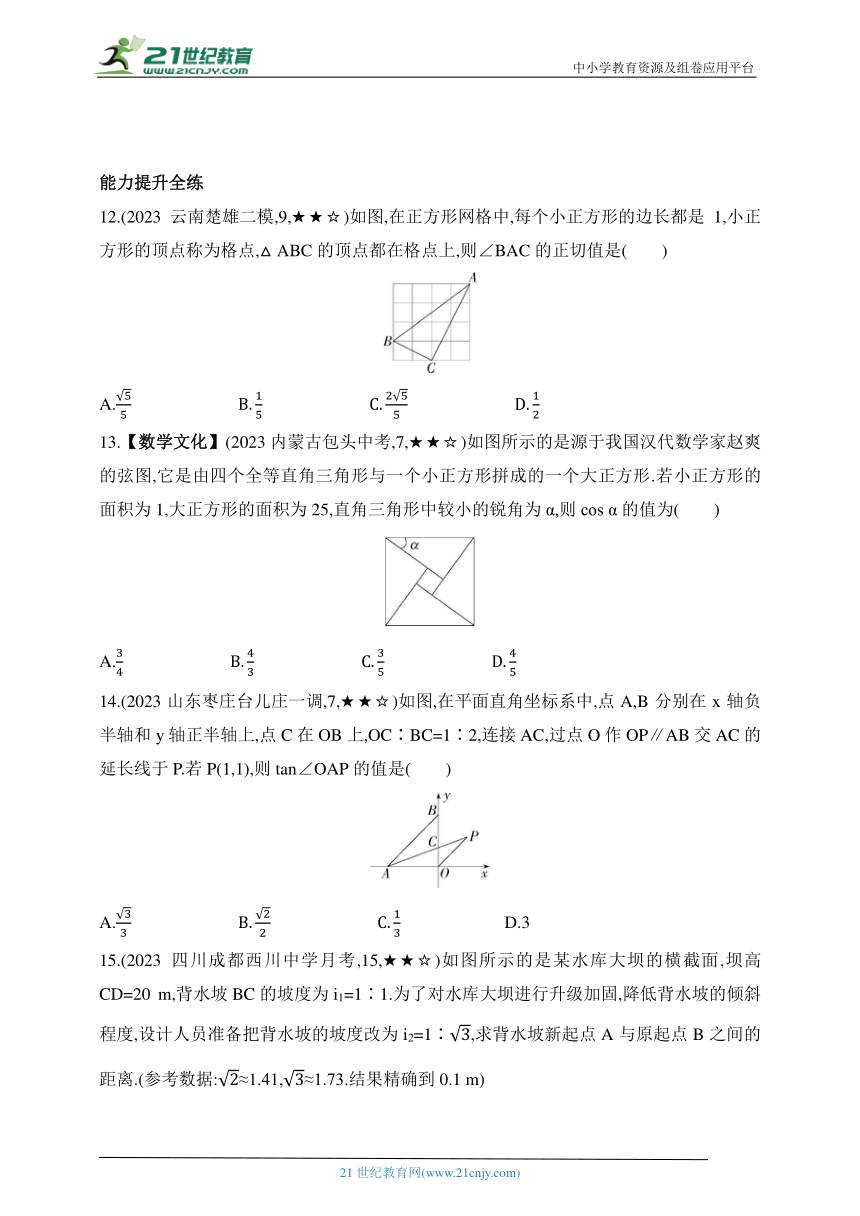
12.(2023云南楚雄二模,9,★★☆)如图,在正方形网格中,每个小正方形的边长都是1,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正切值是( )
A.
13.【数学文化】(2023内蒙古包头中考,7,★★☆)如图所示的是源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为α,则cos α的值为( )
A.
14.(2023山东枣庄台儿庄一调,7,★★☆)如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC∶BC=1∶2,连接AC,过点O作OP∥AB交AC的延长线于P.若P(1,1),则tan∠OAP的值是( )
A. D.3
15.(2023四川成都西川中学月考,15,★★☆)如图所示的是某水库大坝的横截面,坝高CD=20 m,背水坡BC的坡度为i1=1∶1.为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡度改为i2=1∶,求背水坡新起点A与原起点B之间的距离.(参考数据:≈1.41,≈1.73.结果精确到0.1 m)
素养探究全练
16.【创新意识】数学老师布置了这样一个问题:
如果α,β都为锐角,且tan α=,tan β=,求α+β的度数.
甲、乙两名同学想利用正方形网格图来解决这个问题,他们分别设计了图①和图②.
(1)请你分别利用图①、图②求出α+β的度数;
(2)请参考以上解决问题的方法,选择一种方法解决下面的问题:
如果α,β都为锐角,当tan α=5,tan β=时,在图③的正方形网格中,利用已作出的锐角α,画出∠MON,使得∠MON=α-β,并求出α-β的度数.
图① 图②
图③
答案全解全析
基础过关全练
1.B Rt△ABC中,∵∠C=90°,AC=2,AB=3,∴BC=,∴tan B=.故选B.
2.3
解析 过点A作AB⊥x轴于B,
∵点A(2,t)在第一象限,
∴AB=t,OB=2,
又∵tan α=,∴t=3.
故答案为3.
3.解析 ∵AB=AC,AD平分∠BAC,
∴BD=CD,AD⊥BC,
∴tan B=BD.
∵AD2+BD2=AB2,∴+BD2=102,
∴BD=8.∴BC=2BD=16.
4.解析 设OA=x m,则AB=(x+2)m.
由题意知∠AOB=90°,OB=6 m.
在Rt△AOB中,OA2+OB2=AB2,
即x2+62=(x+2)2,解得x=8,∴OA=8 m,
∴tan∠ABO=.
5.C ∵迎水坡AB的坡度i=1∶2,∴,
∵BC=30 m,∴AC=2BC=60 m,
由勾股定理得AB=≈67(m),故选C.
6.C 如图,∵sin A=,∴设BC=4x,AB=5x,
∴AC=3x,∴3x=6,解得x=2,∴AB=10.故选C.
7.B 由题意得BC⊥AB,在Rt△ABC中,∠CAB=α,AB=x米,∴AC=(米),∴A,C两处相距米,故选B.
8.C ∵在Rt△ABC中,∠C=90°,AB=13,AC=5,
∴BC==12,
∴tan B=,tan A=,sin A=,cos B=,故选C.
9.解析 ∵∠C=90°,AC=3,BC=4,
∴AB==5,
∴sin A=,cos A=,tan A=.
10.解析 ∵在Rt△ABD中,tan∠BAD=,
∴BD=AD·tan∠BAD=12×=9.
∴CD=BC-BD=14-9=5.
∴AC==13.
∴sin C=.
11.解析 (1)如图,过点B作BH⊥OA于H,
∵OB=5,sin∠BOA=,∴BH=3,
∴OH==4,∴点B的坐标为(4,3).
(2)易知OA=10,∴AH=OA-OH=10-4=6,
∴在Rt△AHB中,tan∠BAO=.
能力提升全练
12.D 由题意得AB2=32+42=25,BC2=12+22=5,AC2=22+42=20,∴AC2+BC2=AB2,∴△ABC是直角三角形,且∠ACB=90°,∴tan∠BAC=,故选D.
13.D ∵小正方形的面积为1,大正方形的面积为25,∴小正方形的边长为 1,大正方形的边长为5,设直角三角形较短的直角边长为a,则较长的直角边长为a+1,其中a>0,由勾股定理得a2+(a+1)2=52,解得a=3(负值舍去),∴a+1=4,∴cos α=.故选D.
14.C 如图,过点P作PQ⊥x轴于点Q,∵OP∥AB,∴△OCP∽△BCA,∴CP∶AC=OC∶BC=1∶2,∵∠AOC=∠AQP=90°,∴CO∥PQ,∴OQ∶AO=CP∶AC=1∶2,∵P(1,1),∴PQ=OQ=1,∴AO=2,∴tan∠OAP=.故选C.
15.解析 在Rt△BCD中,∵BC的坡度为i1=1∶1,
∴=1,∴CD=BD=20米,
在Rt△ACD中,∵AC的坡度为i2=1∶,
∴(米),
∴AB=AD-BD=20-20≈14.6(米),
∴背水坡新起点A与原起点B之间的距离约为14.6米.
素养探究全练
16.解析 (1)如图①.
在△AMC和△CNB中,
∵AM=CN,∠AMC=∠CNB=90°,MC=NB,
∴△AMC≌△CNB,
∴AC=CB,∠ACM=∠CBN.
∵∠BCN+∠CBN=90°,∴∠ACM+∠BCN=90°,
∴∠ACB=90°,∴∠CAB=∠CBA=45°,即α+β=45°.
图① 图②
如图②,连接BE.
设每个小正方形的边长均为1,
则CE=1,AE=2,BE=,
∴.
又∵∠CEB=∠BEA,∴△CEB∽△BEA,
∴∠CBE=∠BAE=α,
∴∠BED=∠CBE+∠ECB=α+β.
∵DE=DB,∠D=90°,
∴∠BED=45°,∴α+β=45°.
(2)如图③,∠MOE=α,∠NOH=β,则∠MON=α-β,
图③
在△MFN和△NHO中,
∵MF=NH,∠MFN=∠NHO=90°,FN=HO,
∴△MFN≌△NHO,
∴MN=NO,∠MNF=∠NOH.
∵∠NOH+∠ONH=90°,
∴∠ONH+∠MNF=90°,∴∠MNO=90°,
∴∠MON=∠NMO=45°,即α-β=45°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
第一章 直角三角形的边角关系
1 锐角三角函数
基础过关全练
知识点1 正切
1.(2023陕西西安高级中学初中部四模)如图,在Rt△ABC中,∠C=90°,AC=2,AB=3,则tan B的值为( )
A.
2.(2023浙江衢州实验学校月考)如图,点A(2,t)在第一象限,OA与x轴所夹的锐角为α,tan α=,则t的值是 .
3.【教材变式·P4随堂练习T1】如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=10,tan B=,求BC的长.
4.【新独家原创】小明放风筝时风筝线断了,风筝挂在了树上A处(如图),他先拉住风筝线垂直到地面上,发现风筝线多出2 m,然后把风筝线沿直线向右拉6 m,发现风筝线末端B刚好接触地面,请你求出这时∠ABO的正切值.
知识点2 坡度(或坡比)与坡角
5.(2023云南昆明官渡二模)如图,某大坝某段横截面迎水坡AB的坡度i=1∶2,若坝高BC=30 m,则坡面AB的长度约为(参考数据:≈1.41,≈1.73,≈2.24)( )
A.52 m B.60 m C.67 m D.90 m
知识点3 正弦、余弦
6.【教材变式·P5例2】(2023浙江金华模拟)在Rt△ABC中,∠C=90°,AC=6,sin A=,则AB的值为( )
A.8 B.9 C.10 D.7.5
7.(2023四川南充中考)如图,小兵同学从A处出发向正东方向走x米到达B处,再向正北方向走到C处,已知∠BAC=α,则A,C两处相距( )
A.米 B.米
C.x·sin α米 D. x·cos α米
知识点4 三角函数
8.(2023陕西西安未央期末)如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,下列结论中,正确的是( )
A.tan B= B.tan A=
C.sin A= D.cos B=
9.(2023天津红桥模拟)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,求sin A,cos A,tan A的值.(M9201001)
10.如图,在△ABC中,AD⊥BC,垂足为D,若BC=14,AD=12,tan∠BAD=,求sin C的值.
11.如图,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.
(1)求点B的坐标;
(2)求tan∠BAO的值.
能力提升全练
12.(2023云南楚雄二模,9,★★☆)如图,在正方形网格中,每个小正方形的边长都是1,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正切值是( )
A.
13.【数学文化】(2023内蒙古包头中考,7,★★☆)如图所示的是源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为α,则cos α的值为( )
A.
14.(2023山东枣庄台儿庄一调,7,★★☆)如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC∶BC=1∶2,连接AC,过点O作OP∥AB交AC的延长线于P.若P(1,1),则tan∠OAP的值是( )
A. D.3
15.(2023四川成都西川中学月考,15,★★☆)如图所示的是某水库大坝的横截面,坝高CD=20 m,背水坡BC的坡度为i1=1∶1.为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡度改为i2=1∶,求背水坡新起点A与原起点B之间的距离.(参考数据:≈1.41,≈1.73.结果精确到0.1 m)
素养探究全练
16.【创新意识】数学老师布置了这样一个问题:
如果α,β都为锐角,且tan α=,tan β=,求α+β的度数.
甲、乙两名同学想利用正方形网格图来解决这个问题,他们分别设计了图①和图②.
(1)请你分别利用图①、图②求出α+β的度数;
(2)请参考以上解决问题的方法,选择一种方法解决下面的问题:
如果α,β都为锐角,当tan α=5,tan β=时,在图③的正方形网格中,利用已作出的锐角α,画出∠MON,使得∠MON=α-β,并求出α-β的度数.
图① 图②
图③
答案全解全析
基础过关全练
1.B Rt△ABC中,∵∠C=90°,AC=2,AB=3,∴BC=,∴tan B=.故选B.
2.3
解析 过点A作AB⊥x轴于B,
∵点A(2,t)在第一象限,
∴AB=t,OB=2,
又∵tan α=,∴t=3.
故答案为3.
3.解析 ∵AB=AC,AD平分∠BAC,
∴BD=CD,AD⊥BC,
∴tan B=BD.
∵AD2+BD2=AB2,∴+BD2=102,
∴BD=8.∴BC=2BD=16.
4.解析 设OA=x m,则AB=(x+2)m.
由题意知∠AOB=90°,OB=6 m.
在Rt△AOB中,OA2+OB2=AB2,
即x2+62=(x+2)2,解得x=8,∴OA=8 m,
∴tan∠ABO=.
5.C ∵迎水坡AB的坡度i=1∶2,∴,
∵BC=30 m,∴AC=2BC=60 m,
由勾股定理得AB=≈67(m),故选C.
6.C 如图,∵sin A=,∴设BC=4x,AB=5x,
∴AC=3x,∴3x=6,解得x=2,∴AB=10.故选C.
7.B 由题意得BC⊥AB,在Rt△ABC中,∠CAB=α,AB=x米,∴AC=(米),∴A,C两处相距米,故选B.
8.C ∵在Rt△ABC中,∠C=90°,AB=13,AC=5,
∴BC==12,
∴tan B=,tan A=,sin A=,cos B=,故选C.
9.解析 ∵∠C=90°,AC=3,BC=4,
∴AB==5,
∴sin A=,cos A=,tan A=.
10.解析 ∵在Rt△ABD中,tan∠BAD=,
∴BD=AD·tan∠BAD=12×=9.
∴CD=BC-BD=14-9=5.
∴AC==13.
∴sin C=.
11.解析 (1)如图,过点B作BH⊥OA于H,
∵OB=5,sin∠BOA=,∴BH=3,
∴OH==4,∴点B的坐标为(4,3).
(2)易知OA=10,∴AH=OA-OH=10-4=6,
∴在Rt△AHB中,tan∠BAO=.
能力提升全练
12.D 由题意得AB2=32+42=25,BC2=12+22=5,AC2=22+42=20,∴AC2+BC2=AB2,∴△ABC是直角三角形,且∠ACB=90°,∴tan∠BAC=,故选D.
13.D ∵小正方形的面积为1,大正方形的面积为25,∴小正方形的边长为 1,大正方形的边长为5,设直角三角形较短的直角边长为a,则较长的直角边长为a+1,其中a>0,由勾股定理得a2+(a+1)2=52,解得a=3(负值舍去),∴a+1=4,∴cos α=.故选D.
14.C 如图,过点P作PQ⊥x轴于点Q,∵OP∥AB,∴△OCP∽△BCA,∴CP∶AC=OC∶BC=1∶2,∵∠AOC=∠AQP=90°,∴CO∥PQ,∴OQ∶AO=CP∶AC=1∶2,∵P(1,1),∴PQ=OQ=1,∴AO=2,∴tan∠OAP=.故选C.
15.解析 在Rt△BCD中,∵BC的坡度为i1=1∶1,
∴=1,∴CD=BD=20米,
在Rt△ACD中,∵AC的坡度为i2=1∶,
∴(米),
∴AB=AD-BD=20-20≈14.6(米),
∴背水坡新起点A与原起点B之间的距离约为14.6米.
素养探究全练
16.解析 (1)如图①.
在△AMC和△CNB中,
∵AM=CN,∠AMC=∠CNB=90°,MC=NB,
∴△AMC≌△CNB,
∴AC=CB,∠ACM=∠CBN.
∵∠BCN+∠CBN=90°,∴∠ACM+∠BCN=90°,
∴∠ACB=90°,∴∠CAB=∠CBA=45°,即α+β=45°.
图① 图②
如图②,连接BE.
设每个小正方形的边长均为1,
则CE=1,AE=2,BE=,
∴.
又∵∠CEB=∠BEA,∴△CEB∽△BEA,
∴∠CBE=∠BAE=α,
∴∠BED=∠CBE+∠ECB=α+β.
∵DE=DB,∠D=90°,
∴∠BED=45°,∴α+β=45°.
(2)如图③,∠MOE=α,∠NOH=β,则∠MON=α-β,
图③
在△MFN和△NHO中,
∵MF=NH,∠MFN=∠NHO=90°,FN=HO,
∴△MFN≌△NHO,
∴MN=NO,∠MNF=∠NOH.
∵∠NOH+∠ONH=90°,
∴∠ONH+∠MNF=90°,∴∠MNO=90°,
∴∠MON=∠NMO=45°,即α-β=45°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
