2024北师大版数学九年级下学期课时练--3.3垂径定理同步练习(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--3.3垂径定理同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 483.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
第三章 圆
*3 垂径定理
基础过关全练
知识点1 垂径定理
1.如图,DC是☉O的直径,弦AB⊥CD于F,连接BC,DB,则下列结论不一定正确的是( )
A. B.AF=BF C.OF=CF D.
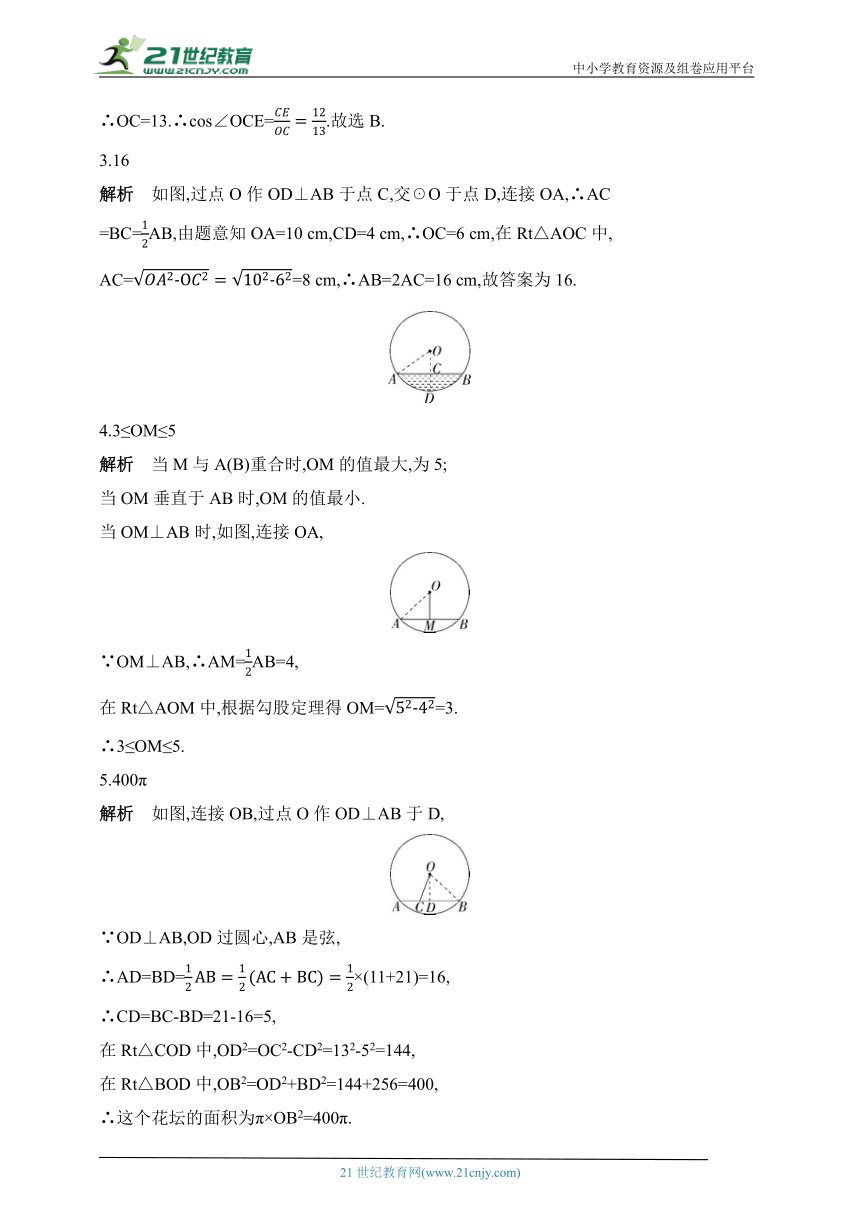
2.(2022云南中考)如图,已知AB是☉O的直径,CD是☉O的弦,AB⊥CD,垂足为E.若AB=26,CD=24,则∠OCE的余弦值为( )
A.
3.【教材变式·P76习题3.3T2】(2023湖南永州中考)如图,☉O是一个盛有水的容器的横截面,☉O的半径为10 cm,水的最深处到水面AB的距离为4 cm,则水面AB的宽度为 cm.
4.如图,☉O的半径为5,弦AB=8,点M是弦AB上的动点,则线段OM的长度的取值范围为 .
5.(2022上海中考)如图,小区内有一个圆形花坛,O为圆心,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为 .(结果保留π)
6.【新独家原创】【方程思想】如图所示的是某博物馆珍藏的元代瓷盘示意图,瓷盘在底座内同时与A,B接触,根据图中的数据(单位:
cm),可知瓷盘的直径为 cm.
7.如图,AB为☉O的弦,C,D是直线AB上两点,且AC=BD.求证:∠C=∠D.
知识点2 垂径定理的推论
8.下列说法:①平分弧的直径垂直平分弧所对的弦;②平分弦的直径平分弦所对的弧;③垂直于弦的直线必过圆心;④垂直于弦的直径平分弦所对的弧.其中正确的是( )
A.②③ B.①③
C.②④ D.①④
9.(2023湖北宜昌中考)如图,OA,OB,OC都是☉O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为( )
A.5 B.4
C.3 D.2
能力提升全练
10.【一题多变】【易错题】(2022江苏东台月考改编,22,★★☆)已知☉O的直径为10,AB、CD是两条平行的弦,且AB=6,CD=8,则AB、CD之间的距离为 .
[变式·增加背景]一下水管道横截面为圆形,直径为100 cm,下雨前水面宽为60 cm,一场大雨过后,水面宽为80 cm,则水面上升了 .
11.【教材变式·P76随堂练习T1】(2023浙江温州期末,23,★★☆)根据素材解决问题.
设计货船通过圆形桥拱的方案
素 材 1 图1中有一座圆拱石桥,图2是其圆形桥拱的示意图,测得水面宽AB=16 m,拱顶离水面的距离CD=4 m 图1 图2
素 材 2 如图3,一艘货船露出水面部分的横截面为矩形EFGH,测得EF=3 m,EH=10 m.因水深足够,货船可以根据需要运载货物.据调查,船身下降的高度y(米)与货船增加的载重量x(吨)满足函数关系式y=x 图3
问题解决
任务1 确定桥拱半径 求圆形桥拱的半径
任务2 拟定设计方案 根据图3状态,货船能否通过圆形桥拱 若能,最多还能卸载多少吨货物 若不能,至少要增加多少吨货物才能通过
素养探究全练
12.【几何直观】【教材变式·P77T4】某广场内欲建造一个如图所示的圆形大花坛,并在大花坛内的M点处建一个亭子,再经过亭子修一条笔直的小路(小路的两端均在圆上).
(1)如何设计小路才能使亭子M位于小路的中点处 在图中画出表示小路的线段.
(2)若大花坛的直径为30米,花坛中心O到亭子M的距离为10米,则(1)中设计的小路有多长 (结果保留根号)
13.【应用意识】【新独家原创】方明是一个爱动手动脑的孩子,他在造一个蒸馒头用的篦子,如图,先画一个直径为32 cm的圆圈,作一条直径AB,再取四等分点M、O、N,O为圆心,过M、N、O分别作垂直于直径AB的弦CD、GH、EF.请你帮助方明计算一共需要多长的竹子.(竹子宽度忽略不计.≈1.7,结果保留整数)
答案全解全析
基础过关全练
1.C ∵DC是☉O的直径,弦AB⊥CD,∴点D是的中点,点C是的中点,且AF=BF,故选项A、B、D中的结论一定正确;无法证明OF=CF.故选C.
2.B ∵AB是☉O的直径,AB⊥CD,∴CE=DE=CD=12,∵AB=26,
∴OC=13.∴cos∠OCE=.故选B.
3.16
解析 如图,过点O作OD⊥AB于点C,交☉O于点D,连接OA,∴AC
=BC=AB,由题意知OA=10 cm,CD=4 cm,∴OC=6 cm,在Rt△AOC中,
AC==8 cm,∴AB=2AC=16 cm,故答案为16.
4.3≤OM≤5
解析 当M与A(B)重合时,OM的值最大,为5;
当OM垂直于AB时,OM的值最小.
当OM⊥AB时,如图,连接OA,
∵OM⊥AB,∴AM=AB=4,
在Rt△AOM中,根据勾股定理得OM==3.
∴3≤OM≤5.
5.400π
解析 如图,连接OB,过点O作OD⊥AB于D,
∵OD⊥AB,OD过圆心,AB是弦,
∴AD=BD=×(11+21)=16,
∴CD=BC-BD=21-16=5,
在Rt△COD中,OD2=OC2-CD2=132-52=144,
在Rt△BOD中,OB2=OD2+BD2=144+256=400,
∴这个花坛的面积为π×OB2=400π.
6.15
解析 如图,设圆心为O,过O作OD⊥AB,交AB于C,交☉O于D,连接OA.
由垂径定理得AC=BC=AB=6 cm.
设☉O的半径为r cm,则OC=(r-3)cm.
在Rt△AOC中,由勾股定理得OA2=AC2+OC2,
即r2=62+(r-3)2,解得r=7.5.∴2r=2×7.5=15.
故瓷盘的直径为15 cm.
7.证明 如图,过点O作OH⊥AB于点H.
∵AB是☉O的弦,∴AH=BH.
∵AC=BD,
∴AC+AH=BD+BH,即CH=DH.
又OH⊥AB,∴OH垂直平分CD.
∴OC=OD.∴∠C=∠D.
8.D 平分弦(不是直径)的直径平分弦所对的弧,故②错误;垂直于弦且平分弦的直线必过圆心,故③错误.①④正确.故选D.
9.B ∵AD=CD=8,OB为☉O的半径,∴OB⊥AC,
在Rt△AOD中,OA==10,
∴OB=10,∴BD=10-6=4.故选B.
能力提升全练
10.1或7
解析 ∵☉O的直径为10,∴☉O的半径为5,
分为两种情况:
①如图1,过O作OF⊥AB于F,交CD于E,连接OC、OA,
∵AB∥CD,∴OE⊥CD,∵AB=6,CD=8,
∴CE=ED=AB=3,
在Rt△OCE中,OC=5,CE=4,
∴OE==3,
在Rt△OAF中,OA=5,AF=3,
∴OF==4,
∴EF=OF-OE=4-3=1,
即两条平行弦AB与CD之间的距离是1;
②如图2,由①知两条平行弦AB与CD之间的距离是3+4=7.
综上所述,两条平行弦AB与CD之间的距离是1或7.
图1 图2
易错警示 本题易只考虑AB、CD在同侧而出错.
[变式] 10 cm或70 cm
解析 如图,AB为下雨前水面,A'B'或A″B″为下雨后的水面,作OC⊥AB于C,交A'B'于C',连接OB,OB',则OC'⊥A'B',
当水面上升到A'B'时,
由垂径定理得BC=AB=30 cm,B'C'=A'B'=40 cm,
在Rt△OBC中,OC==40(cm),
在Rt△OB'C'中,OC'==30(cm),
则水面上升的高度为40-30=10(cm);
当水面上升到A″B″时,同理可知水面上升的高度为40+30=70(cm).
综上可得,水面上升的高度为10 cm或70 cm.
11.解析 任务1:如图,设圆心为点O,连接OA,OD,易知C,D,O三点共线.
设桥拱的半径为r m,则OA=r m,OD=(r-4)m,
∵OC⊥AB,∴AD=BD=AB=8 m,
∵OD2+AD2=OA2,∴(r-4)2+82=r2,∴r=10,∴圆形桥拱的半径为10 m.
任务2:当EH是☉O的弦时,假设F、G在弦AB上,设EH与OC的交点为M,连接OE,OH,如图,
∵四边形EFGH为矩形,∴EH∥FG,
∵OC⊥AB,∴OM⊥EH,∴EM=EH=5 m,∴OM= m,∵OD=6 m,∴DM=(5-6<3,∴货船不能通过圆形桥拱.船在水面部分至少需下降的高度为3-(5)m.
令y=9-5,则9-5,∴至少要增加(900-500)吨的货物才能通过.
素养探究全练
12.解析 (1)如图,连接OM,过点M作OM的垂线,交☉O于A,B两点,则线段AB即为要修的小路.
(2)如图,连接OB.
由题意得OM=10米,OB=×30=15(米).
在Rt△BOM中,BM=米,
∴AB=2BM=10米.
答:(1)中设计的小路长10米.
13.解析 由题意可得AB=EF=32 cm,连接OC.
∵M、O、N是AB的四等分点,
∴OM=×32=8(cm),
在Rt△OCM中,OC=×32=16(cm),
∴CM=(cm),
由垂径定理得CD=2CM=2×8(cm).
同理得GH=CD=16 cm.
AB+CD+EF+GH=2AB+2CD=2×32+2×16≈64+32×1.7=118.4≈119(cm).
答:一共需要119 cm长的竹子.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
第三章 圆
*3 垂径定理
基础过关全练
知识点1 垂径定理
1.如图,DC是☉O的直径,弦AB⊥CD于F,连接BC,DB,则下列结论不一定正确的是( )
A. B.AF=BF C.OF=CF D.
2.(2022云南中考)如图,已知AB是☉O的直径,CD是☉O的弦,AB⊥CD,垂足为E.若AB=26,CD=24,则∠OCE的余弦值为( )
A.
3.【教材变式·P76习题3.3T2】(2023湖南永州中考)如图,☉O是一个盛有水的容器的横截面,☉O的半径为10 cm,水的最深处到水面AB的距离为4 cm,则水面AB的宽度为 cm.
4.如图,☉O的半径为5,弦AB=8,点M是弦AB上的动点,则线段OM的长度的取值范围为 .
5.(2022上海中考)如图,小区内有一个圆形花坛,O为圆心,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为 .(结果保留π)
6.【新独家原创】【方程思想】如图所示的是某博物馆珍藏的元代瓷盘示意图,瓷盘在底座内同时与A,B接触,根据图中的数据(单位:
cm),可知瓷盘的直径为 cm.
7.如图,AB为☉O的弦,C,D是直线AB上两点,且AC=BD.求证:∠C=∠D.
知识点2 垂径定理的推论
8.下列说法:①平分弧的直径垂直平分弧所对的弦;②平分弦的直径平分弦所对的弧;③垂直于弦的直线必过圆心;④垂直于弦的直径平分弦所对的弧.其中正确的是( )
A.②③ B.①③
C.②④ D.①④
9.(2023湖北宜昌中考)如图,OA,OB,OC都是☉O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为( )
A.5 B.4
C.3 D.2
能力提升全练
10.【一题多变】【易错题】(2022江苏东台月考改编,22,★★☆)已知☉O的直径为10,AB、CD是两条平行的弦,且AB=6,CD=8,则AB、CD之间的距离为 .
[变式·增加背景]一下水管道横截面为圆形,直径为100 cm,下雨前水面宽为60 cm,一场大雨过后,水面宽为80 cm,则水面上升了 .
11.【教材变式·P76随堂练习T1】(2023浙江温州期末,23,★★☆)根据素材解决问题.
设计货船通过圆形桥拱的方案
素 材 1 图1中有一座圆拱石桥,图2是其圆形桥拱的示意图,测得水面宽AB=16 m,拱顶离水面的距离CD=4 m 图1 图2
素 材 2 如图3,一艘货船露出水面部分的横截面为矩形EFGH,测得EF=3 m,EH=10 m.因水深足够,货船可以根据需要运载货物.据调查,船身下降的高度y(米)与货船增加的载重量x(吨)满足函数关系式y=x 图3
问题解决
任务1 确定桥拱半径 求圆形桥拱的半径
任务2 拟定设计方案 根据图3状态,货船能否通过圆形桥拱 若能,最多还能卸载多少吨货物 若不能,至少要增加多少吨货物才能通过
素养探究全练
12.【几何直观】【教材变式·P77T4】某广场内欲建造一个如图所示的圆形大花坛,并在大花坛内的M点处建一个亭子,再经过亭子修一条笔直的小路(小路的两端均在圆上).
(1)如何设计小路才能使亭子M位于小路的中点处 在图中画出表示小路的线段.
(2)若大花坛的直径为30米,花坛中心O到亭子M的距离为10米,则(1)中设计的小路有多长 (结果保留根号)
13.【应用意识】【新独家原创】方明是一个爱动手动脑的孩子,他在造一个蒸馒头用的篦子,如图,先画一个直径为32 cm的圆圈,作一条直径AB,再取四等分点M、O、N,O为圆心,过M、N、O分别作垂直于直径AB的弦CD、GH、EF.请你帮助方明计算一共需要多长的竹子.(竹子宽度忽略不计.≈1.7,结果保留整数)
答案全解全析
基础过关全练
1.C ∵DC是☉O的直径,弦AB⊥CD,∴点D是的中点,点C是的中点,且AF=BF,故选项A、B、D中的结论一定正确;无法证明OF=CF.故选C.
2.B ∵AB是☉O的直径,AB⊥CD,∴CE=DE=CD=12,∵AB=26,
∴OC=13.∴cos∠OCE=.故选B.
3.16
解析 如图,过点O作OD⊥AB于点C,交☉O于点D,连接OA,∴AC
=BC=AB,由题意知OA=10 cm,CD=4 cm,∴OC=6 cm,在Rt△AOC中,
AC==8 cm,∴AB=2AC=16 cm,故答案为16.
4.3≤OM≤5
解析 当M与A(B)重合时,OM的值最大,为5;
当OM垂直于AB时,OM的值最小.
当OM⊥AB时,如图,连接OA,
∵OM⊥AB,∴AM=AB=4,
在Rt△AOM中,根据勾股定理得OM==3.
∴3≤OM≤5.
5.400π
解析 如图,连接OB,过点O作OD⊥AB于D,
∵OD⊥AB,OD过圆心,AB是弦,
∴AD=BD=×(11+21)=16,
∴CD=BC-BD=21-16=5,
在Rt△COD中,OD2=OC2-CD2=132-52=144,
在Rt△BOD中,OB2=OD2+BD2=144+256=400,
∴这个花坛的面积为π×OB2=400π.
6.15
解析 如图,设圆心为O,过O作OD⊥AB,交AB于C,交☉O于D,连接OA.
由垂径定理得AC=BC=AB=6 cm.
设☉O的半径为r cm,则OC=(r-3)cm.
在Rt△AOC中,由勾股定理得OA2=AC2+OC2,
即r2=62+(r-3)2,解得r=7.5.∴2r=2×7.5=15.
故瓷盘的直径为15 cm.
7.证明 如图,过点O作OH⊥AB于点H.
∵AB是☉O的弦,∴AH=BH.
∵AC=BD,
∴AC+AH=BD+BH,即CH=DH.
又OH⊥AB,∴OH垂直平分CD.
∴OC=OD.∴∠C=∠D.
8.D 平分弦(不是直径)的直径平分弦所对的弧,故②错误;垂直于弦且平分弦的直线必过圆心,故③错误.①④正确.故选D.
9.B ∵AD=CD=8,OB为☉O的半径,∴OB⊥AC,
在Rt△AOD中,OA==10,
∴OB=10,∴BD=10-6=4.故选B.
能力提升全练
10.1或7
解析 ∵☉O的直径为10,∴☉O的半径为5,
分为两种情况:
①如图1,过O作OF⊥AB于F,交CD于E,连接OC、OA,
∵AB∥CD,∴OE⊥CD,∵AB=6,CD=8,
∴CE=ED=AB=3,
在Rt△OCE中,OC=5,CE=4,
∴OE==3,
在Rt△OAF中,OA=5,AF=3,
∴OF==4,
∴EF=OF-OE=4-3=1,
即两条平行弦AB与CD之间的距离是1;
②如图2,由①知两条平行弦AB与CD之间的距离是3+4=7.
综上所述,两条平行弦AB与CD之间的距离是1或7.
图1 图2
易错警示 本题易只考虑AB、CD在同侧而出错.
[变式] 10 cm或70 cm
解析 如图,AB为下雨前水面,A'B'或A″B″为下雨后的水面,作OC⊥AB于C,交A'B'于C',连接OB,OB',则OC'⊥A'B',
当水面上升到A'B'时,
由垂径定理得BC=AB=30 cm,B'C'=A'B'=40 cm,
在Rt△OBC中,OC==40(cm),
在Rt△OB'C'中,OC'==30(cm),
则水面上升的高度为40-30=10(cm);
当水面上升到A″B″时,同理可知水面上升的高度为40+30=70(cm).
综上可得,水面上升的高度为10 cm或70 cm.
11.解析 任务1:如图,设圆心为点O,连接OA,OD,易知C,D,O三点共线.
设桥拱的半径为r m,则OA=r m,OD=(r-4)m,
∵OC⊥AB,∴AD=BD=AB=8 m,
∵OD2+AD2=OA2,∴(r-4)2+82=r2,∴r=10,∴圆形桥拱的半径为10 m.
任务2:当EH是☉O的弦时,假设F、G在弦AB上,设EH与OC的交点为M,连接OE,OH,如图,
∵四边形EFGH为矩形,∴EH∥FG,
∵OC⊥AB,∴OM⊥EH,∴EM=EH=5 m,∴OM= m,∵OD=6 m,∴DM=(5-6<3,∴货船不能通过圆形桥拱.船在水面部分至少需下降的高度为3-(5)m.
令y=9-5,则9-5,∴至少要增加(900-500)吨的货物才能通过.
素养探究全练
12.解析 (1)如图,连接OM,过点M作OM的垂线,交☉O于A,B两点,则线段AB即为要修的小路.
(2)如图,连接OB.
由题意得OM=10米,OB=×30=15(米).
在Rt△BOM中,BM=米,
∴AB=2BM=10米.
答:(1)中设计的小路长10米.
13.解析 由题意可得AB=EF=32 cm,连接OC.
∵M、O、N是AB的四等分点,
∴OM=×32=8(cm),
在Rt△OCM中,OC=×32=16(cm),
∴CM=(cm),
由垂径定理得CD=2CM=2×8(cm).
同理得GH=CD=16 cm.
AB+CD+EF+GH=2AB+2CD=2×32+2×16≈64+32×1.7=118.4≈119(cm).
答:一共需要119 cm长的竹子.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
