2024北师大版数学九年级下学期课时练--1.3 三角函数的计算同步练习(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--1.3 三角函数的计算同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 377.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 17:27:13 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
第一章 直角三角形的边角关系
3 三角函数的计算
基础过关全练
知识点1 利用计算器求锐角的三角函数值
1.(2023山东莱阳期末)若用科学计算器计算sin 42°16',按键顺序正确的是( )
A.sin42·16=
B.sin42DMS16=
C.sin42DMS16DMS=
D.2ndfsin42DMS16=
2.用计算器求下列各式的值(结果精确到0.000 1).
(1)sin 89°;(2)cos 45.32°;(3)tan 60°25'41″;(4)sin 72°38'25″.
知识点2 已知三角函数值,用计算器求锐角
3.已知sin A=0.178 2,则锐角A的度数大约为( )
A.8° B.9° C.10° D.11°
4.【新独家原创】等腰三角形的一边长为另一边长的2倍,在用科学计算器求底角的度数时,具体按键顺序是( )
A.SHIFTsin0·25=
B.sin0·25SHIFT=
C.SHIFTcos0·25=
D.cos0·25SHIFT=
5.(2023河南漯河临颍模拟)如图,有一滑梯AB,其水平宽度AC为5.3米,铅直高度BC为2.8米,则∠A的度数约为 (用科学计算器计算,结果精确到0.1°).
知识点3 三角函数的实际应用
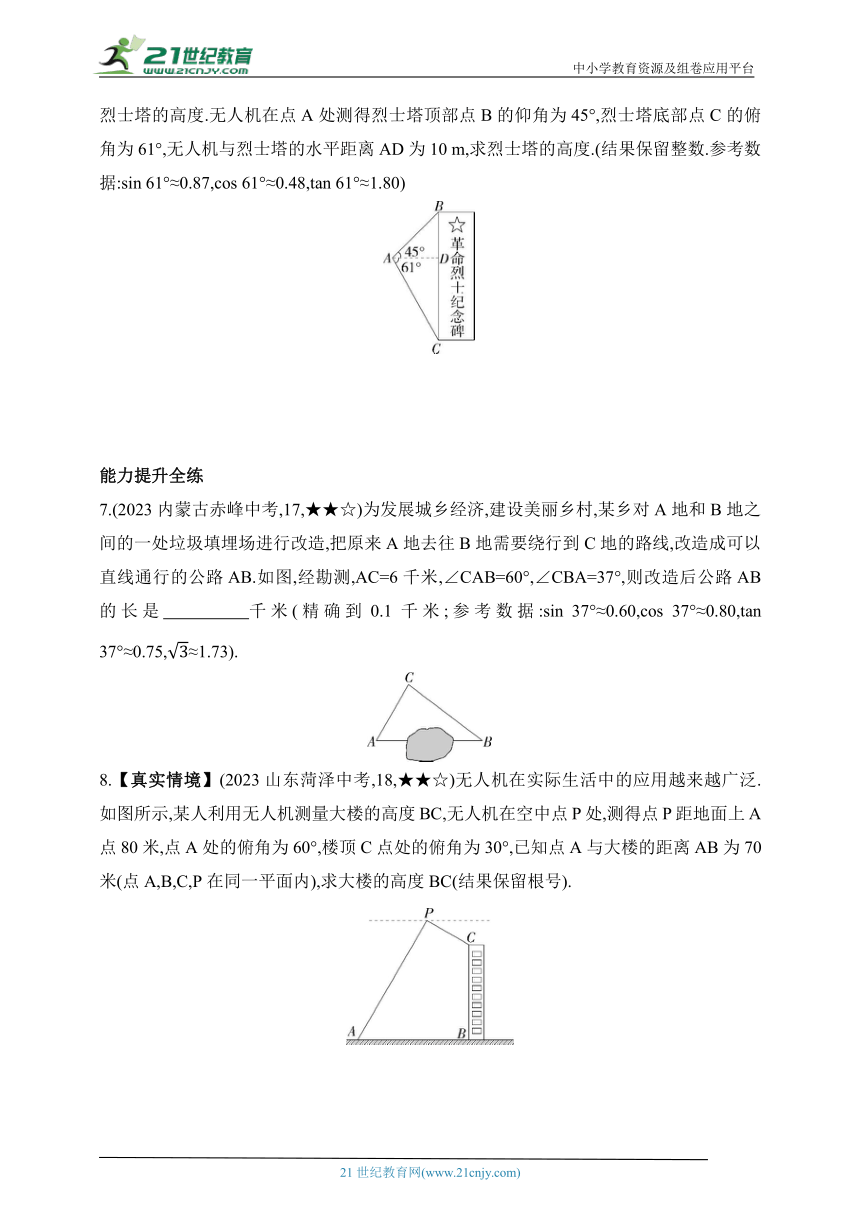
6.【革命文化】【教材变式·P15T4】(2022湖北襄阳中考)位于岘山的革命烈士纪念塔是襄阳市的标志性建筑,是为纪念“襄樊战役”中牺牲的革命烈士及第一、第二次国内革命战争时期为襄阳的解放事业献身的革命烈士而兴建的,某校数学兴趣小组利用无人机测量烈士塔的高度.无人机在点A处测得烈士塔顶部点B的仰角为45°,烈士塔底部点C的俯角为61°,无人机与烈士塔的水平距离AD为10 m,求烈士塔的高度.(结果保留整数.参考数据:sin 61°≈0.87,cos 61°≈0.48,tan 61°≈1.80)
能力提升全练
7.(2023内蒙古赤峰中考,17,★★☆)为发展城乡经济,建设美丽乡村,某乡对A地和B地之间的一处垃圾填埋场进行改造,把原来A地去往B地需要绕行到C地的路线,改造成可以直线通行的公路AB.如图,经勘测,AC=6千米,∠CAB=60°,∠CBA=37°,则改造后公路AB的长是 千米(精确到0.1千米;参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73).
8.【真实情境】(2023山东菏泽中考,18,★★☆)无人机在实际生活中的应用越来越广泛.如图所示,某人利用无人机测量大楼的高度BC,无人机在空中点P处,测得点P距地面上A点80米,点A处的俯角为60°,楼顶C点处的俯角为30°,已知点A与大楼的距离AB为70米(点A,B,C,P在同一平面内),求大楼的高度BC(结果保留根号).
素养探究全练
9.【推理能力】
(1)通过计算(可用计算器),比较下列各对数的大小,并提出你的猜想:
①sin 30° 2sin 15°cos 15°;
②sin 36° 2sin 18°cos 18°;
③sin 45° 2sin 22.5°cos 22.5°;
④sin 60° 2sin 30°cos 30°;
⑤sin 80° 2sin 40°cos 40°.
猜想:已知0°<α<45°,则sin 2α 2sin αcos α.
(2)如图,在△ABC中,AB=AC=1,∠BAC=2α,请根据提示,利用面积法验证结论.
答案全解全析
基础过关全练
1.C
2.解析 (1)sin 89°≈0.999 8.
(2)cos 45.32°≈0.703 1.
(3)tan 60°25'41″≈1.762 3.
(4)sin 72°38'25″≈0.954 5.
3.C 正确使用计算器计算即可.使用SHIFT键,然后按sin0·1782即可求出∠A的度数.
4.C 由题意可知,等腰三角形的腰长应为底边长的2倍,如图,△ABC中,AB=AC=2BC,过A作AD⊥BC于D,则BD=BC,则cos B==0.25.
按照利用计算器由已知三角函数值求锐角度数的步骤进行按键即可,故选C.
5.27.8°
解析 ∵tan A=≈0.528 3,
∴∠A≈27.8°,
故答案为27.8°.
6.解析 由题意得∠BAD=45°,∠DAC=61°,
在Rt△ABD中,∠BAD=45°,AD=10 m,
∴BD=AD=10 m,
在Rt△ACD中,∠DAC=61°,
∴tan 61°=≈1.80,
解得CD≈18(m),
∴BC=BD+CD=10+18=28(m).
∴烈士塔的高度约为28 m.
能力提升全练
7.9.9
解析 过点C作CD⊥AB于点D,
在Rt△ADC中,AC=6千米,∠CAB=60°,cos∠CAB=,sin∠CAB=,
∴AD=AC·cos∠CAB=6cos 60°=3(千米),
CD=AC·sin∠CAB=6sin 60°=3(千米),
在Rt△CDB中,∠CBA=37°,CD=3千米,tan∠CBA=,
∴DB=(千米),
∴AB=AD+DB=3+4≈3+4×1.73≈9.9(千米).
故改造后公路AB的长约是9.9千米.
8.解析 过P作PH⊥AB于H,过C作CQ⊥PH于Q,如图所示,
∵CB⊥AB,∴四边形CQHB是矩形,
∴QH=BC,BH=CQ,
由题意可得AP=80米,∠PAH=60°,∠PCQ=30°,AB=70米,
∴PH=AP·sin 60°=80×(米),
AH=AP·cos 60°=80×=40(米),
∴CQ=BH=AB-AH=70-40=30(米),
∴PQ=CQ·tan 30°=10(米),
∴BC=QH=40(米),
∴大楼的高度BC为30米.
素养探究全练
9.解析 (1)①sin 30°=2sin 15°cos 15°.
②sin 36°=2sin 18°cos 18°.
③sin 45°=2sin 22.5°cos 22.5°.
④sin 60°=2sin 30°cos 30°.
⑤sin 80°=2sin 40°cos 40°.
猜想:已知0°<α<45°,则sin 2α=2sin αcos α.
(2)证明:∵S△ABC=BE·AC=AB·sin 2α·AC,
S△ABC=BC·AD=×2ABsin α·ACcos α,
∴AB·sin 2α·AC=×2ABsin α·ACcos α,
∴sin 2α=2sin αcos α.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
第一章 直角三角形的边角关系
3 三角函数的计算
基础过关全练
知识点1 利用计算器求锐角的三角函数值
1.(2023山东莱阳期末)若用科学计算器计算sin 42°16',按键顺序正确的是( )
A.sin42·16=
B.sin42DMS16=
C.sin42DMS16DMS=
D.2ndfsin42DMS16=
2.用计算器求下列各式的值(结果精确到0.000 1).
(1)sin 89°;(2)cos 45.32°;(3)tan 60°25'41″;(4)sin 72°38'25″.
知识点2 已知三角函数值,用计算器求锐角
3.已知sin A=0.178 2,则锐角A的度数大约为( )
A.8° B.9° C.10° D.11°
4.【新独家原创】等腰三角形的一边长为另一边长的2倍,在用科学计算器求底角的度数时,具体按键顺序是( )
A.SHIFTsin0·25=
B.sin0·25SHIFT=
C.SHIFTcos0·25=
D.cos0·25SHIFT=
5.(2023河南漯河临颍模拟)如图,有一滑梯AB,其水平宽度AC为5.3米,铅直高度BC为2.8米,则∠A的度数约为 (用科学计算器计算,结果精确到0.1°).
知识点3 三角函数的实际应用
6.【革命文化】【教材变式·P15T4】(2022湖北襄阳中考)位于岘山的革命烈士纪念塔是襄阳市的标志性建筑,是为纪念“襄樊战役”中牺牲的革命烈士及第一、第二次国内革命战争时期为襄阳的解放事业献身的革命烈士而兴建的,某校数学兴趣小组利用无人机测量烈士塔的高度.无人机在点A处测得烈士塔顶部点B的仰角为45°,烈士塔底部点C的俯角为61°,无人机与烈士塔的水平距离AD为10 m,求烈士塔的高度.(结果保留整数.参考数据:sin 61°≈0.87,cos 61°≈0.48,tan 61°≈1.80)
能力提升全练
7.(2023内蒙古赤峰中考,17,★★☆)为发展城乡经济,建设美丽乡村,某乡对A地和B地之间的一处垃圾填埋场进行改造,把原来A地去往B地需要绕行到C地的路线,改造成可以直线通行的公路AB.如图,经勘测,AC=6千米,∠CAB=60°,∠CBA=37°,则改造后公路AB的长是 千米(精确到0.1千米;参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73).
8.【真实情境】(2023山东菏泽中考,18,★★☆)无人机在实际生活中的应用越来越广泛.如图所示,某人利用无人机测量大楼的高度BC,无人机在空中点P处,测得点P距地面上A点80米,点A处的俯角为60°,楼顶C点处的俯角为30°,已知点A与大楼的距离AB为70米(点A,B,C,P在同一平面内),求大楼的高度BC(结果保留根号).
素养探究全练
9.【推理能力】
(1)通过计算(可用计算器),比较下列各对数的大小,并提出你的猜想:
①sin 30° 2sin 15°cos 15°;
②sin 36° 2sin 18°cos 18°;
③sin 45° 2sin 22.5°cos 22.5°;
④sin 60° 2sin 30°cos 30°;
⑤sin 80° 2sin 40°cos 40°.
猜想:已知0°<α<45°,则sin 2α 2sin αcos α.
(2)如图,在△ABC中,AB=AC=1,∠BAC=2α,请根据提示,利用面积法验证结论.
答案全解全析
基础过关全练
1.C
2.解析 (1)sin 89°≈0.999 8.
(2)cos 45.32°≈0.703 1.
(3)tan 60°25'41″≈1.762 3.
(4)sin 72°38'25″≈0.954 5.
3.C 正确使用计算器计算即可.使用SHIFT键,然后按sin0·1782即可求出∠A的度数.
4.C 由题意可知,等腰三角形的腰长应为底边长的2倍,如图,△ABC中,AB=AC=2BC,过A作AD⊥BC于D,则BD=BC,则cos B==0.25.
按照利用计算器由已知三角函数值求锐角度数的步骤进行按键即可,故选C.
5.27.8°
解析 ∵tan A=≈0.528 3,
∴∠A≈27.8°,
故答案为27.8°.
6.解析 由题意得∠BAD=45°,∠DAC=61°,
在Rt△ABD中,∠BAD=45°,AD=10 m,
∴BD=AD=10 m,
在Rt△ACD中,∠DAC=61°,
∴tan 61°=≈1.80,
解得CD≈18(m),
∴BC=BD+CD=10+18=28(m).
∴烈士塔的高度约为28 m.
能力提升全练
7.9.9
解析 过点C作CD⊥AB于点D,
在Rt△ADC中,AC=6千米,∠CAB=60°,cos∠CAB=,sin∠CAB=,
∴AD=AC·cos∠CAB=6cos 60°=3(千米),
CD=AC·sin∠CAB=6sin 60°=3(千米),
在Rt△CDB中,∠CBA=37°,CD=3千米,tan∠CBA=,
∴DB=(千米),
∴AB=AD+DB=3+4≈3+4×1.73≈9.9(千米).
故改造后公路AB的长约是9.9千米.
8.解析 过P作PH⊥AB于H,过C作CQ⊥PH于Q,如图所示,
∵CB⊥AB,∴四边形CQHB是矩形,
∴QH=BC,BH=CQ,
由题意可得AP=80米,∠PAH=60°,∠PCQ=30°,AB=70米,
∴PH=AP·sin 60°=80×(米),
AH=AP·cos 60°=80×=40(米),
∴CQ=BH=AB-AH=70-40=30(米),
∴PQ=CQ·tan 30°=10(米),
∴BC=QH=40(米),
∴大楼的高度BC为30米.
素养探究全练
9.解析 (1)①sin 30°=2sin 15°cos 15°.
②sin 36°=2sin 18°cos 18°.
③sin 45°=2sin 22.5°cos 22.5°.
④sin 60°=2sin 30°cos 30°.
⑤sin 80°=2sin 40°cos 40°.
猜想:已知0°<α<45°,则sin 2α=2sin αcos α.
(2)证明:∵S△ABC=BE·AC=AB·sin 2α·AC,
S△ABC=BC·AD=×2ABsin α·ACcos α,
∴AB·sin 2α·AC=×2ABsin α·ACcos α,
∴sin 2α=2sin αcos α.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
