2024北师大版数学九年级下学期课时练--4 解直角三角形同步练习(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--4 解直角三角形同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 456.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 17:29:49 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
第一章 直角三角形的边角关系
4 解直角三角形
基础过关全练
知识点 解直角三角形
1.在△ABC中,∠C=90°,AB=4,AC=3,欲求∠A的值,最适宜的做法是( )
A.计算tan A的值求出
B.计算sin A的值求出
C.计算cos A的值求出
D.先根据sin B求出∠B,再利用90°-∠B求出
2.(2023广西桂平期末)如图,某超市电梯的截面图中,AB的长为15米,AB与AC的夹角为α,则高BC是( )
A.15sin α米 B.15cos α米
C.米 D.米
3.(2022陕西中考)如图,AD是△ABC的高.若BD=2CD=6,tan C=2,则边AB的长为( )
A.3
4.【新独家原创】在△ABC中,AB=17,AC=13,∠B=45°,则cos A= .
5.【教材变式·P17T1】在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,求下列直角三角形中的未知量.
(1)c=8,∠A=60°;(2)b=2,c=4;(3)a=6,∠B=30°.
能力提升全练
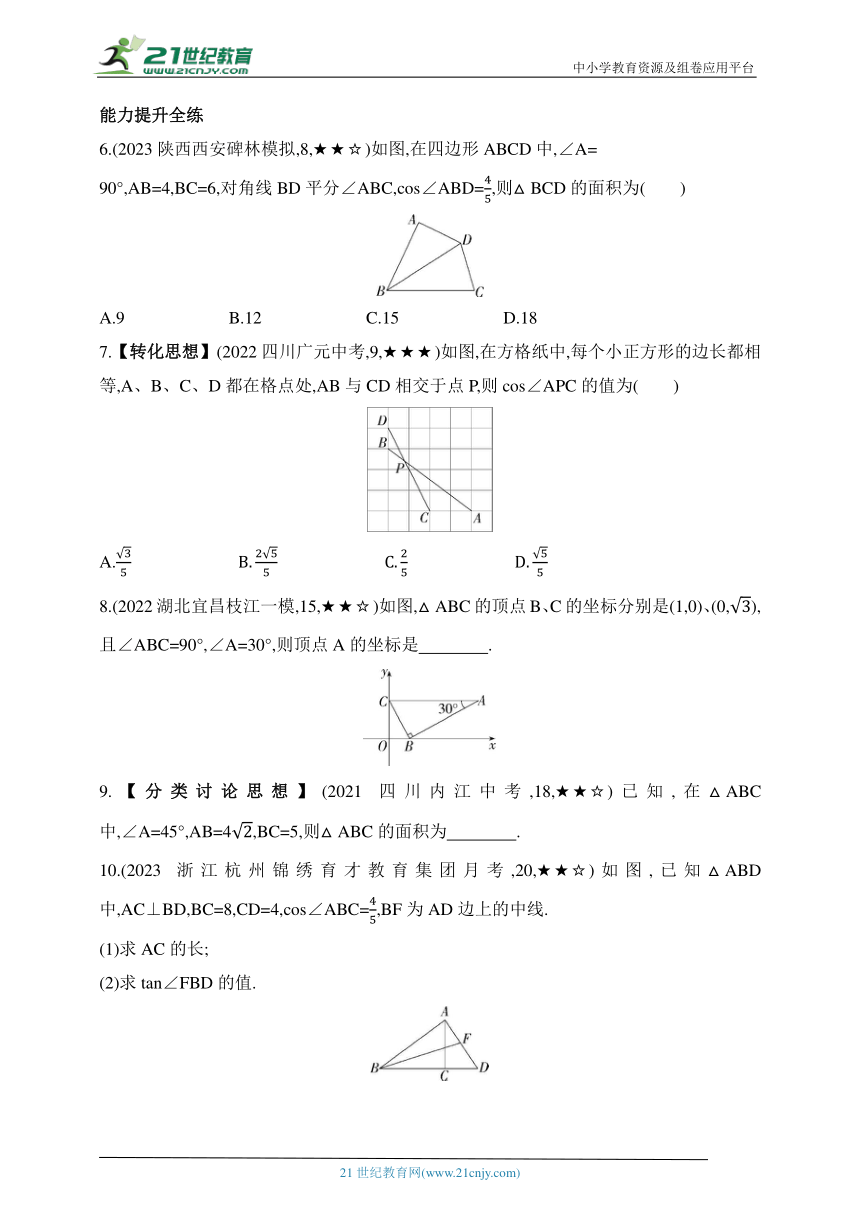
6.(2023陕西西安碑林模拟,8,★★☆)如图,在四边形ABCD中,∠A=
90°,AB=4,BC=6,对角线BD平分∠ABC,cos∠ABD=,则△BCD的面积为( )
A.9 B.12 C.15 D.18
7.【转化思想】(2022四川广元中考,9,★★★)如图,在方格纸中,每个小正方形的边长都相等,A、B、C、D都在格点处,AB与CD相交于点P,则cos∠APC的值为( )
A.
8.(2022湖北宜昌枝江一模,15,★★☆)如图,△ABC的顶点B、C的坐标分别是(1,0)、(0,),且∠ABC=90°,∠A=30°,则顶点A的坐标是 .
9.【分类讨论思想】(2021四川内江中考,18,★★☆)已知,在△ABC中,∠A=45°,AB=4,BC=5,则△ABC的面积为 .
10.(2023浙江杭州锦绣育才教育集团月考,20,★★☆)如图,已知△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
(2)求tan∠FBD的值.
11.(2022江苏宿迁泗洪二模,24,★★☆)
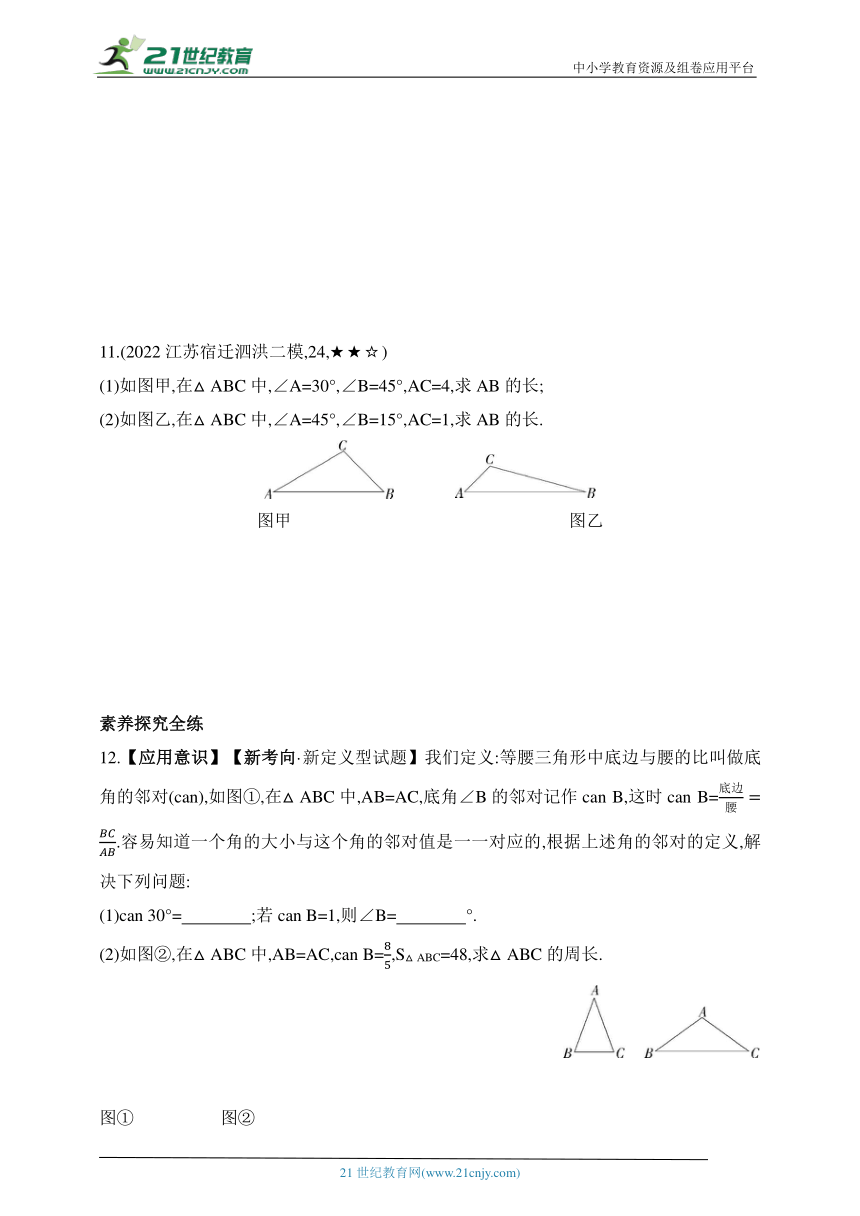
(1)如图甲,在△ABC中,∠A=30°,∠B=45°,AC=4,求AB的长;
(2)如图乙,在△ABC中,∠A=45°,∠B=15°,AC=1,求AB的长.
图甲 图乙
素养探究全练
12.【应用意识】【新考向·新定义型试题】我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图①,在△ABC中,AB=AC,底角∠B的邻对记作can B,这时can B=.容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解决下列问题:
(1)can 30°= ;若can B=1,则∠B= °.
(2)如图②,在△ABC中,AB=AC,can B=,S△ABC=48,求△ABC的周长.
图① 图②
答案全解全析
基础过关全练
1.C ∵在Rt△ABC中,∠C=90°,AB=4,AC=3,
∴cos A=,∴欲求∠A的值,最适宜的做法是计算cos A的值求出,故选C.
2.A 在Rt△ABC中,sin α=,∵AB的长为15米,
∴BC=15sin α米,故选A.
3.D ∵2CD=6,∴CD=3,
∵tan C=2,∴=2,∴AD=6,
在Rt△ABD中,由勾股定理得AB=,故选D.
4.
解析 如图,过C作CD⊥AB,垂足为D,
在Rt△BCD中,∠B=45°,∠BCD=90°-45°=45°,
∴∠B=∠BCD,∴BD=CD.
设BD=CD=x,则AD=AB-BD=17-x,
在Rt△ACD中,AD2+DC2=AC2,
∴(17-x)2+x2=132,解得x=5或x=12,
∴AD=5或AD=12.
∴cos A=或cos A=.
5.解析 (1)∠B=90°-∠A=90°-60°=30°.
∵sin A=,∴a=c·sin A=8×.
∵cos A=,∴b=c·cos A=8×=4.
(2)∵a2+b2=c2,∴a=.
∵cos A=,
∴∠A=45°,
∴∠B=90°-∠A=45°.
(3)∠A=90°-∠B=90°-30°=60°.
∵tan B=,∴b=a·tan B=6×.
∵cos B=.
能力提升全练
6.A 过点D作DE⊥BC,垂足为E,如图,
∵对角线BD平分∠ABC,DE⊥BC,∠A=90°,
∴DE=AD,
∵∠A=90°,AB=4,∴cos∠ABD==3,∴S△BCD=BC·DE=×6×3=9.故选A.
7.B 如图,把AB向上平移一个格到DE,连接CE,则DE∥AB,
∴∠APC=∠EDC.
设每个小正方形的边长均为1,则在△DCE中,EC==5,∴EC2+DC2=DE2,故△DCE为直角三角形,且∠DCE=90°.∴cos∠APC=cos∠EDC=.
8.(4,)
解析 过点A作AG⊥x轴,交x轴于点G.
∵B、C的坐标分别是(1,0)、(0,),
∴OC=,OB=1,
∴BC==2.
∵∠ABC=90°,∠BAC=30°,
∴AB=.
∵∠ABG+∠CBO=90°,∠BCO+∠CBO=90°,
∴∠ABG=∠BCO.
∴sin∠ABG=,cos∠ABG=,BG=3.∴OG=1+3=4,
∴顶点A的坐标是(4,).
9.2或14
解析 过点B作BD⊥AC,垂足为点D,在Rt△ABD中,∠A=45°,
AB=4,∴BD=AD=4,在Rt△BDC中,BC=5,∴CD==3.
①如图1,当△ABC是钝角三角形时,AC=AD-CD=1,
∴S△ABC=AC·BD=×1×4=2;
②如图2,当△ABC是锐角三角形时,AC=AD+CD=7,
∴S△ABC=AC·BD=×7×4=14.故答案为2或14.
图1 图2
10.解析 (1)∵AC⊥BD,BC=8,
∴cos∠ABC=,
∴AB=10,
在Rt△ACB中,由勾股定理得AC==6.
(2)在Rt△ACD中,由勾股定理得AD=,
如图,连接CF,过F点作FE⊥BD,垂足E,
∵BF为AD边上的中线,即F为AD的中点,
∴CF=,
∵FE⊥CD,
∴CE=CD=2,
在Rt△EFC中, EF==3,
∴tan∠FBD=.
11.解析 (1)如图1,过C点作CD⊥AB于点D.
在Rt△ACD中,AC=4,∠A=30°,
∴CD=,
在Rt△BCD中,∠B=45°,∴BD=CD=2,
∴AB=AD+BD=2+2.
(2)如图2,过C点作CD⊥AB于点D,在BD上取点E,使CE=BE,连接CE,
∴∠BCE=∠B=15°,
∴∠CED=∠BCE+∠B=30°.
在Rt△ACD中,∠A=45°,AC=1,
∴AD=CD=,
在Rt△CDE中,∠CED=30°,
∴DE=,
∴BE=CE=,
∴AB=AD+DE+BE=.
图1 图2
素养探究全练
12.解析 (1);60.
详解:①如图,△ABC中,AB=AC,∠B=30°,过A作AD⊥BC于D.
设AD=x,则AB=2x,BD=x,
∴BC=2x,∴can 30°=can B=.
②在△ABC中,AB=AC,若can B=1,则=1,
∴BC=AB=AC,
∴△ABC为等边三角形,∴∠B=60°.
(2)如图,过点A作AH⊥BC,垂足为H.
∵can B=.
∴设BC=8x,AB=AC=5x.
∵AB=AC,AH⊥BC,∴BH=BC=4x,
∴AH==3x.
∵S△ABC=48,∴BC· AH=48,即×8x×3x=48,
∴x2=4,∴x=2(负值舍去),
∴AB=AC=10,BC=16,
∴AB+AC+BC=10+10+16=36,
即△ABC的周长为36.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
第一章 直角三角形的边角关系
4 解直角三角形
基础过关全练
知识点 解直角三角形
1.在△ABC中,∠C=90°,AB=4,AC=3,欲求∠A的值,最适宜的做法是( )
A.计算tan A的值求出
B.计算sin A的值求出
C.计算cos A的值求出
D.先根据sin B求出∠B,再利用90°-∠B求出
2.(2023广西桂平期末)如图,某超市电梯的截面图中,AB的长为15米,AB与AC的夹角为α,则高BC是( )
A.15sin α米 B.15cos α米
C.米 D.米
3.(2022陕西中考)如图,AD是△ABC的高.若BD=2CD=6,tan C=2,则边AB的长为( )
A.3
4.【新独家原创】在△ABC中,AB=17,AC=13,∠B=45°,则cos A= .
5.【教材变式·P17T1】在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,求下列直角三角形中的未知量.
(1)c=8,∠A=60°;(2)b=2,c=4;(3)a=6,∠B=30°.
能力提升全练
6.(2023陕西西安碑林模拟,8,★★☆)如图,在四边形ABCD中,∠A=
90°,AB=4,BC=6,对角线BD平分∠ABC,cos∠ABD=,则△BCD的面积为( )
A.9 B.12 C.15 D.18
7.【转化思想】(2022四川广元中考,9,★★★)如图,在方格纸中,每个小正方形的边长都相等,A、B、C、D都在格点处,AB与CD相交于点P,则cos∠APC的值为( )
A.
8.(2022湖北宜昌枝江一模,15,★★☆)如图,△ABC的顶点B、C的坐标分别是(1,0)、(0,),且∠ABC=90°,∠A=30°,则顶点A的坐标是 .
9.【分类讨论思想】(2021四川内江中考,18,★★☆)已知,在△ABC中,∠A=45°,AB=4,BC=5,则△ABC的面积为 .
10.(2023浙江杭州锦绣育才教育集团月考,20,★★☆)如图,已知△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
(2)求tan∠FBD的值.
11.(2022江苏宿迁泗洪二模,24,★★☆)
(1)如图甲,在△ABC中,∠A=30°,∠B=45°,AC=4,求AB的长;
(2)如图乙,在△ABC中,∠A=45°,∠B=15°,AC=1,求AB的长.
图甲 图乙
素养探究全练
12.【应用意识】【新考向·新定义型试题】我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图①,在△ABC中,AB=AC,底角∠B的邻对记作can B,这时can B=.容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解决下列问题:
(1)can 30°= ;若can B=1,则∠B= °.
(2)如图②,在△ABC中,AB=AC,can B=,S△ABC=48,求△ABC的周长.
图① 图②
答案全解全析
基础过关全练
1.C ∵在Rt△ABC中,∠C=90°,AB=4,AC=3,
∴cos A=,∴欲求∠A的值,最适宜的做法是计算cos A的值求出,故选C.
2.A 在Rt△ABC中,sin α=,∵AB的长为15米,
∴BC=15sin α米,故选A.
3.D ∵2CD=6,∴CD=3,
∵tan C=2,∴=2,∴AD=6,
在Rt△ABD中,由勾股定理得AB=,故选D.
4.
解析 如图,过C作CD⊥AB,垂足为D,
在Rt△BCD中,∠B=45°,∠BCD=90°-45°=45°,
∴∠B=∠BCD,∴BD=CD.
设BD=CD=x,则AD=AB-BD=17-x,
在Rt△ACD中,AD2+DC2=AC2,
∴(17-x)2+x2=132,解得x=5或x=12,
∴AD=5或AD=12.
∴cos A=或cos A=.
5.解析 (1)∠B=90°-∠A=90°-60°=30°.
∵sin A=,∴a=c·sin A=8×.
∵cos A=,∴b=c·cos A=8×=4.
(2)∵a2+b2=c2,∴a=.
∵cos A=,
∴∠A=45°,
∴∠B=90°-∠A=45°.
(3)∠A=90°-∠B=90°-30°=60°.
∵tan B=,∴b=a·tan B=6×.
∵cos B=.
能力提升全练
6.A 过点D作DE⊥BC,垂足为E,如图,
∵对角线BD平分∠ABC,DE⊥BC,∠A=90°,
∴DE=AD,
∵∠A=90°,AB=4,∴cos∠ABD==3,∴S△BCD=BC·DE=×6×3=9.故选A.
7.B 如图,把AB向上平移一个格到DE,连接CE,则DE∥AB,
∴∠APC=∠EDC.
设每个小正方形的边长均为1,则在△DCE中,EC==5,∴EC2+DC2=DE2,故△DCE为直角三角形,且∠DCE=90°.∴cos∠APC=cos∠EDC=.
8.(4,)
解析 过点A作AG⊥x轴,交x轴于点G.
∵B、C的坐标分别是(1,0)、(0,),
∴OC=,OB=1,
∴BC==2.
∵∠ABC=90°,∠BAC=30°,
∴AB=.
∵∠ABG+∠CBO=90°,∠BCO+∠CBO=90°,
∴∠ABG=∠BCO.
∴sin∠ABG=,cos∠ABG=,BG=3.∴OG=1+3=4,
∴顶点A的坐标是(4,).
9.2或14
解析 过点B作BD⊥AC,垂足为点D,在Rt△ABD中,∠A=45°,
AB=4,∴BD=AD=4,在Rt△BDC中,BC=5,∴CD==3.
①如图1,当△ABC是钝角三角形时,AC=AD-CD=1,
∴S△ABC=AC·BD=×1×4=2;
②如图2,当△ABC是锐角三角形时,AC=AD+CD=7,
∴S△ABC=AC·BD=×7×4=14.故答案为2或14.
图1 图2
10.解析 (1)∵AC⊥BD,BC=8,
∴cos∠ABC=,
∴AB=10,
在Rt△ACB中,由勾股定理得AC==6.
(2)在Rt△ACD中,由勾股定理得AD=,
如图,连接CF,过F点作FE⊥BD,垂足E,
∵BF为AD边上的中线,即F为AD的中点,
∴CF=,
∵FE⊥CD,
∴CE=CD=2,
在Rt△EFC中, EF==3,
∴tan∠FBD=.
11.解析 (1)如图1,过C点作CD⊥AB于点D.
在Rt△ACD中,AC=4,∠A=30°,
∴CD=,
在Rt△BCD中,∠B=45°,∴BD=CD=2,
∴AB=AD+BD=2+2.
(2)如图2,过C点作CD⊥AB于点D,在BD上取点E,使CE=BE,连接CE,
∴∠BCE=∠B=15°,
∴∠CED=∠BCE+∠B=30°.
在Rt△ACD中,∠A=45°,AC=1,
∴AD=CD=,
在Rt△CDE中,∠CED=30°,
∴DE=,
∴BE=CE=,
∴AB=AD+DE+BE=.
图1 图2
素养探究全练
12.解析 (1);60.
详解:①如图,△ABC中,AB=AC,∠B=30°,过A作AD⊥BC于D.
设AD=x,则AB=2x,BD=x,
∴BC=2x,∴can 30°=can B=.
②在△ABC中,AB=AC,若can B=1,则=1,
∴BC=AB=AC,
∴△ABC为等边三角形,∴∠B=60°.
(2)如图,过点A作AH⊥BC,垂足为H.
∵can B=.
∴设BC=8x,AB=AC=5x.
∵AB=AC,AH⊥BC,∴BH=BC=4x,
∴AH==3x.
∵S△ABC=48,∴BC· AH=48,即×8x×3x=48,
∴x2=4,∴x=2(负值舍去),
∴AB=AC=10,BC=16,
∴AB+AC+BC=10+10+16=36,
即△ABC的周长为36.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
