2024北师大版数学九年级下学期课时练--2.5 二次函数与一元二次方程同步练习(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--2.5 二次函数与一元二次方程同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 17:32:51 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
第二章 二次函数
5 二次函数与一元二次方程
基础过关全练
知识点1 二次函数与一元二次方程的关系
1.小兰画了一个函数y=x2+ax+b的图象,如图,则关于x的方程x2+ax+b=0的解是( )
A.无解 B.x=1 C.x=-4 D.x1=-1,x2=4
2.【一题多变·抛物线与x轴有一个交点】(2023湖南郴州中考)已知抛物线y=x2-6x+m与x轴有且只有一个交点,则m= .
[变式1·抛物线与x轴有交点(交点个数不确定)]【易错题】抛物线y=(k-1)x2-4x-4与x轴有公共点,则k的取值范围是 .
[变式2]二次函数y=-2x2-3x+k的图象在x轴下方,则k的取值范围是 .
3.【新独家原创】如果函数y=kx2-kx+4x-1的图象与直线y=x-2有唯一的公共点,那么交点的坐标是 .
4.【数形结合思想】(2021四川乐山中考)已知关于x的一元二次方程x2+x-m=0.
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)二次函数y=x2+x-m的部分图象如图所示,求一元二次方程x2+x-m=0的解.
知识点2 利用二次函数的图象求一元二次方程的近似根
5.(2023陕西汉阴月考)已知二次函数y=-x2-2x+2.
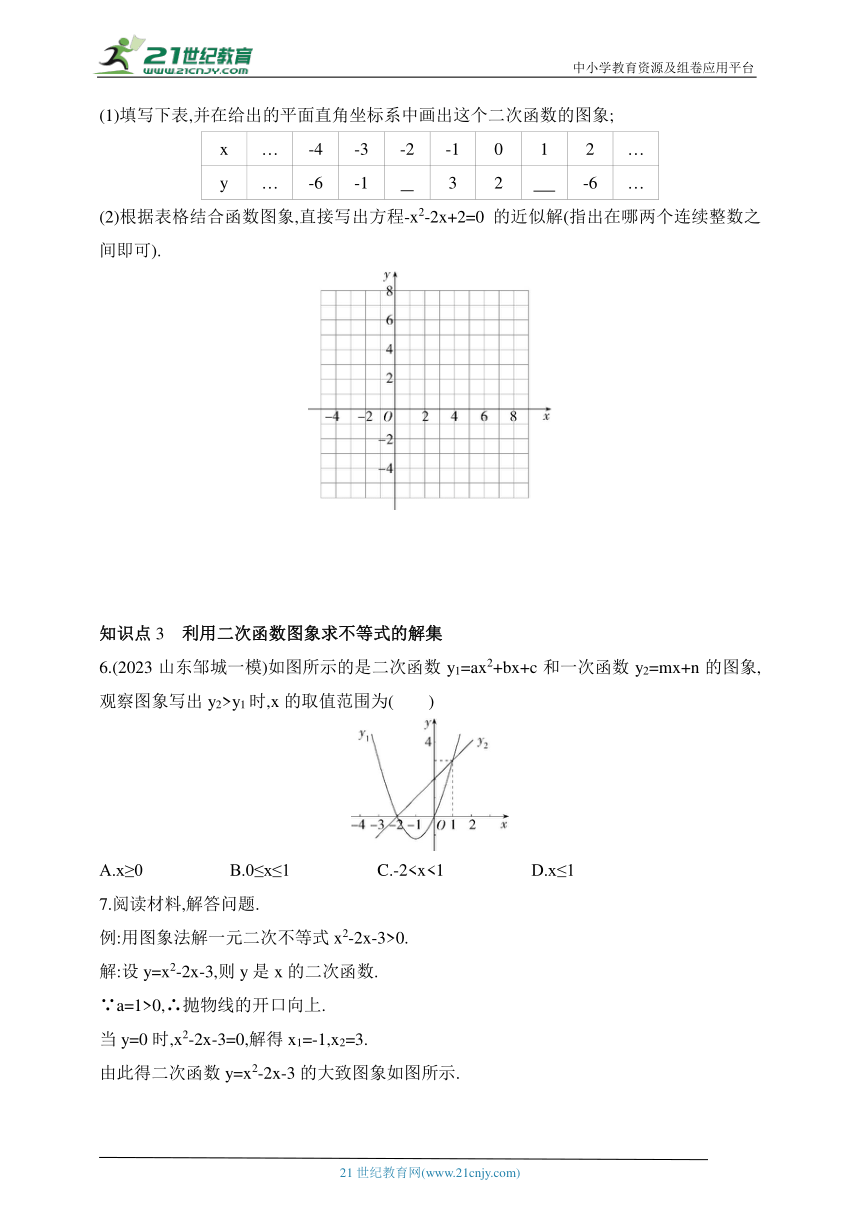
(1)填写下表,并在给出的平面直角坐标系中画出这个二次函数的图象;
x … -4 -3 -2 -1 0 1 2 …
y … -6 -1 3 2 -6 …
(2)根据表格结合函数图象,直接写出方程-x2-2x+2=0的近似解(指出在哪两个连续整数之间即可).
知识点3 利用二次函数图象求不等式的解集
6.(2023山东邹城一模)如图所示的是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2>y1时,x的取值范围为( )
A.x≥0 B.0≤x≤1 C.-27.阅读材料,解答问题.
例:用图象法解一元二次不等式x2-2x-3>0.
解:设y=x2-2x-3,则y是x的二次函数.
∵a=1>0,∴抛物线的开口向上.
当y=0时,x2-2x-3=0,解得x1=-1,x2=3.
由此得二次函数y=x2-2x-3的大致图象如图所示.
观察函数图象可知,当x<-1或x>3时,y>0.
∴x2-2x-3>0的解集是x<-1或x>3.
(1)观察图象,直接写出一元二次不等式x2-2x-3<0的解集: ;
(2)依照上例,用图象法解一元二次不等式x2-1>0.
能力提升全练
8.(2023湖南衡阳中考,12,★★☆)已知m>n>0,若关于x的方程x2+2x-3-m=0的根为x1,x2(x1x4),则下列结论正确的是( )
A.x3C.x19.(2023河北中考,16,★★★)已知二次函数y=-x2+m2x和y=x2-m2(m是常数)的图象与x轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为( )
A.2 B.m2 C.4 D.2m2
素养探究全练
10.【几何直观】(2021四川广元中考)将二次函数y=-x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )
A.-或-3 B.-或-3
C.或-3 D.或-3
11.【创新意识】【新考向·代数推理】(2023云南中考)数和形是数学研究客观物体的两个方面,数(代数)侧重研究物体数量方面,具有精确性.形(几何)侧重研究物体形的方面,具有直观性.数和形相互联系,可用数来反映空间形式,也可用形来说明数量关系.数形结合就是把两者结合起来考虑问题,充分利用代数、几何各自的优势,数形互化,共同解决问题.
同学们,请你结合所学的数学知识解决下列问题.
在平面直角坐标系中,若点的横坐标、纵坐标都为整数,则称这样的点为整点.设函数y=(4a+2)x2+(9-6a)x-4a+4(实数a为常数)的图象为图象T.
(1)求证:无论a取何实数,图象T与x轴总有公共点.
(2)是否存在整数a,使图象T与x轴的公共点中有整点 若存在,求所有整数a的值;若不存在,请说明理由.
答案全解全析
基础过关全练
1.D 由题图可知函数y=x2+ax+b的图象与x轴的交点坐标分别是
(-1,0),(4,0),∴关于x的方程x2+ax+b=0的解为x1=-1,x2=4.故选D.
2.9
解析 ∵抛物线y=x2-6x+m与x轴有且只有一个交点,∴方程x2-6x+m=0有两个相同的实数根,即36-4m=0,解得m=9.故答案为9.
[变式1] k≥0且k≠1
解析 ∵抛物线y=(k-1)x2-4x-4与x轴有公共点,∴k-1≠0,且Δ=(-4)2-4×(k-1)×(-4)≥0,解得k≥0且k≠1.
易错警示 本题易忽略二次函数的二次项系数不为0而出错.
[变式2] k<-
解析 ∵二次函数y=-2x2-3x+k的图象在x轴下方,∴Δ<0,即(-3)2-4×
(-2)·k<0,解得k<-.
3.或(-1,-3)或
解析 (1)当k=0时,原函数为y=4x-1,直线y=4x-1与直线y=x-2有唯一公共点,是.
(2)当k≠0时,原函数为二次函数,
∵其图象与直线y=x-2有唯一公共点,
∴方程kx2-kx+4x-1=x-2即kx2-(k-3)x+1=0有两个相等的实数根,
∴Δ=[-(k-3)]2-4k=0,
即k2-10k+9=0,解得k=1或k=9.
当k=1时,交点坐标是(-1,-3);
当k=9时,交点坐标是.
综上,交点的坐标是或(-1,-3)或.
4.解析 (1)∵一元二次方程x2+x-m=0有两个不相等的实数根,
∴b2-4ac>0,即1+4m>0,∴m>-.
(2)二次函数y=x2+x-m的图象的对称轴为直线x=-,
∴抛物线与x轴的两个交点关于直线x=-对称,
由题图可知抛物线与x轴的一个交点为(1,0),
∴另一个交点为(-2,0),
∴一元二次方程x2+x-m=0的解为x1=1,x2=-2.
5.解析 (1)填表如下:
x … -4 -3 -2 -1 0 1 2 …
y … -6 -1 2 3 2 -1 -6 …
所画图象如图:
(2)由图象可知,方程-x2-2x+2=0的两个近似解在-3~-2之间和0~1之间.
6.C 解答本题的关键是从图象上找出两函数图象的交点坐标,再根据两函数图象的上下位置关系,判断y2>y1时,x的取值范围.从图象上看出,两个交点坐标分别为(-2,0),(1,3),∴当y2>y1时,-27.解析 (1)-1(2)设y=x2-1,则y是x的二次函数.
∵a=1>0,∴抛物线的开口向上.
当y=0时,x2-1=0,解得x=±1.
由此得二次函数y=x2-1的大致图象如图所示.
观察图象可知,当x<-1或x>1时,y>0.
∴x2-1>0的解集是x<-1或x>1.
能力提升全练
8.B 关于x的方程x2+2x-3-m=0的解为抛物线y=x2+2x-3与直线y=m的交点的横坐标,关于x的方程x2+2x-3-n=0的解为抛物线y=x2+2x-3与直线y=n的交点的横坐标,如图:
由图可知,x19.A 在y=-x2+m2x中,令y=0,得-x2+m2x=0,解得x=0或x=m2,在y=x2-m2中,令y=0,得x2-m2=0,解得x=-m或x=m,
由这四个交点中每相邻两点间的距离都相等可知分两种情况:
(1)若m>0,则m2=2m,∴m=2;(2)若m<0,则m2=-2m,∴m=-2.∵抛物线y=x2-m2的对称轴为直线x=0,抛物线y=-x2+m2x的对称轴为直线x=,∴这两个函数图象对称轴之间的距离==2.故选A.
素养探究全练
10.A ∵y=-x2+2x+3=-(x-1)2+4,
∴抛物线y=-x2+2x+3的顶点坐标为(1,4),
当y=0时,-x2+2x+3=0,解得x1=-1,x2=3,
则抛物线y=-x2+2x+3与x轴的交点为A(-1,0),B(3,0),把抛物线y=
-x2+2x+3在x轴上方的部分沿x轴翻折到x轴下方,则翻折部分的抛物线解析式为y=(x-1)2-4(-1如图,当直线y=x+b过点B时,直线y=x+b与新图象恰好有三个公共点,∴3+b=0,解得b=-3;
当直线y=x+b与抛物线y=(x-1)2-4(-111.解析 (1)证明:当4a+2=0,即a=-时,函数表达式为y=12x+6,
令y=0得x=-,
∴此时函数y=(4a+2)x2+(9-6a)x-4a+4(实数a为常数)的图象与x轴有交点;
当4a+2≠0,即a≠-时,y=(4a+2)x2+(9-6a)x-4a+4为二次函数,
∵Δ=(9-6a)2-4(4a+2)(-4a+4)=100a2-140a+49=(10a-7)2≥0,
∴函数y=(4a+2)x2+(9-6a)x-4a+4(实数a为常数)的图象与x轴有交点.
综上所述,无论a取何实数,图象T与x轴总有公共点.
(2)存在整数a,使图象T与x轴的公共点中有整点.当a=-时,不符合题意;当a≠-时,在y=(4a+2)x2+(9-6a)x-4a+4中,令y=0得0=(4a+2)x2+(9-6a)x-4a+4,解得x=-或x=,a是整数,∴当2a+1是6的因数时,是整数,∴2a+1=-6或2a+1=-3或2a+1=-2或2a+1=-1或2a+1=1或2a+1=2或2a+1=3或2a+1=6,解得a=-或a=-2或a=-或a=-1或a=0或a=或a=1或a=,∵a是整数,∴a=-2或a=-1或a=0或a=1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
第二章 二次函数
5 二次函数与一元二次方程
基础过关全练
知识点1 二次函数与一元二次方程的关系
1.小兰画了一个函数y=x2+ax+b的图象,如图,则关于x的方程x2+ax+b=0的解是( )
A.无解 B.x=1 C.x=-4 D.x1=-1,x2=4
2.【一题多变·抛物线与x轴有一个交点】(2023湖南郴州中考)已知抛物线y=x2-6x+m与x轴有且只有一个交点,则m= .
[变式1·抛物线与x轴有交点(交点个数不确定)]【易错题】抛物线y=(k-1)x2-4x-4与x轴有公共点,则k的取值范围是 .
[变式2]二次函数y=-2x2-3x+k的图象在x轴下方,则k的取值范围是 .
3.【新独家原创】如果函数y=kx2-kx+4x-1的图象与直线y=x-2有唯一的公共点,那么交点的坐标是 .
4.【数形结合思想】(2021四川乐山中考)已知关于x的一元二次方程x2+x-m=0.
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)二次函数y=x2+x-m的部分图象如图所示,求一元二次方程x2+x-m=0的解.
知识点2 利用二次函数的图象求一元二次方程的近似根
5.(2023陕西汉阴月考)已知二次函数y=-x2-2x+2.
(1)填写下表,并在给出的平面直角坐标系中画出这个二次函数的图象;
x … -4 -3 -2 -1 0 1 2 …
y … -6 -1 3 2 -6 …
(2)根据表格结合函数图象,直接写出方程-x2-2x+2=0的近似解(指出在哪两个连续整数之间即可).
知识点3 利用二次函数图象求不等式的解集
6.(2023山东邹城一模)如图所示的是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2>y1时,x的取值范围为( )
A.x≥0 B.0≤x≤1 C.-2
例:用图象法解一元二次不等式x2-2x-3>0.
解:设y=x2-2x-3,则y是x的二次函数.
∵a=1>0,∴抛物线的开口向上.
当y=0时,x2-2x-3=0,解得x1=-1,x2=3.
由此得二次函数y=x2-2x-3的大致图象如图所示.
观察函数图象可知,当x<-1或x>3时,y>0.
∴x2-2x-3>0的解集是x<-1或x>3.
(1)观察图象,直接写出一元二次不等式x2-2x-3<0的解集: ;
(2)依照上例,用图象法解一元二次不等式x2-1>0.
能力提升全练
8.(2023湖南衡阳中考,12,★★☆)已知m>n>0,若关于x的方程x2+2x-3-m=0的根为x1,x2(x1
A.x3
A.2 B.m2 C.4 D.2m2
素养探究全练
10.【几何直观】(2021四川广元中考)将二次函数y=-x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )
A.-或-3 B.-或-3
C.或-3 D.或-3
11.【创新意识】【新考向·代数推理】(2023云南中考)数和形是数学研究客观物体的两个方面,数(代数)侧重研究物体数量方面,具有精确性.形(几何)侧重研究物体形的方面,具有直观性.数和形相互联系,可用数来反映空间形式,也可用形来说明数量关系.数形结合就是把两者结合起来考虑问题,充分利用代数、几何各自的优势,数形互化,共同解决问题.
同学们,请你结合所学的数学知识解决下列问题.
在平面直角坐标系中,若点的横坐标、纵坐标都为整数,则称这样的点为整点.设函数y=(4a+2)x2+(9-6a)x-4a+4(实数a为常数)的图象为图象T.
(1)求证:无论a取何实数,图象T与x轴总有公共点.
(2)是否存在整数a,使图象T与x轴的公共点中有整点 若存在,求所有整数a的值;若不存在,请说明理由.
答案全解全析
基础过关全练
1.D 由题图可知函数y=x2+ax+b的图象与x轴的交点坐标分别是
(-1,0),(4,0),∴关于x的方程x2+ax+b=0的解为x1=-1,x2=4.故选D.
2.9
解析 ∵抛物线y=x2-6x+m与x轴有且只有一个交点,∴方程x2-6x+m=0有两个相同的实数根,即36-4m=0,解得m=9.故答案为9.
[变式1] k≥0且k≠1
解析 ∵抛物线y=(k-1)x2-4x-4与x轴有公共点,∴k-1≠0,且Δ=(-4)2-4×(k-1)×(-4)≥0,解得k≥0且k≠1.
易错警示 本题易忽略二次函数的二次项系数不为0而出错.
[变式2] k<-
解析 ∵二次函数y=-2x2-3x+k的图象在x轴下方,∴Δ<0,即(-3)2-4×
(-2)·k<0,解得k<-.
3.或(-1,-3)或
解析 (1)当k=0时,原函数为y=4x-1,直线y=4x-1与直线y=x-2有唯一公共点,是.
(2)当k≠0时,原函数为二次函数,
∵其图象与直线y=x-2有唯一公共点,
∴方程kx2-kx+4x-1=x-2即kx2-(k-3)x+1=0有两个相等的实数根,
∴Δ=[-(k-3)]2-4k=0,
即k2-10k+9=0,解得k=1或k=9.
当k=1时,交点坐标是(-1,-3);
当k=9时,交点坐标是.
综上,交点的坐标是或(-1,-3)或.
4.解析 (1)∵一元二次方程x2+x-m=0有两个不相等的实数根,
∴b2-4ac>0,即1+4m>0,∴m>-.
(2)二次函数y=x2+x-m的图象的对称轴为直线x=-,
∴抛物线与x轴的两个交点关于直线x=-对称,
由题图可知抛物线与x轴的一个交点为(1,0),
∴另一个交点为(-2,0),
∴一元二次方程x2+x-m=0的解为x1=1,x2=-2.
5.解析 (1)填表如下:
x … -4 -3 -2 -1 0 1 2 …
y … -6 -1 2 3 2 -1 -6 …
所画图象如图:
(2)由图象可知,方程-x2-2x+2=0的两个近似解在-3~-2之间和0~1之间.
6.C 解答本题的关键是从图象上找出两函数图象的交点坐标,再根据两函数图象的上下位置关系,判断y2>y1时,x的取值范围.从图象上看出,两个交点坐标分别为(-2,0),(1,3),∴当y2>y1时,-2
∵a=1>0,∴抛物线的开口向上.
当y=0时,x2-1=0,解得x=±1.
由此得二次函数y=x2-1的大致图象如图所示.
观察图象可知,当x<-1或x>1时,y>0.
∴x2-1>0的解集是x<-1或x>1.
能力提升全练
8.B 关于x的方程x2+2x-3-m=0的解为抛物线y=x2+2x-3与直线y=m的交点的横坐标,关于x的方程x2+2x-3-n=0的解为抛物线y=x2+2x-3与直线y=n的交点的横坐标,如图:
由图可知,x1
由这四个交点中每相邻两点间的距离都相等可知分两种情况:
(1)若m>0,则m2=2m,∴m=2;(2)若m<0,则m2=-2m,∴m=-2.∵抛物线y=x2-m2的对称轴为直线x=0,抛物线y=-x2+m2x的对称轴为直线x=,∴这两个函数图象对称轴之间的距离==2.故选A.
素养探究全练
10.A ∵y=-x2+2x+3=-(x-1)2+4,
∴抛物线y=-x2+2x+3的顶点坐标为(1,4),
当y=0时,-x2+2x+3=0,解得x1=-1,x2=3,
则抛物线y=-x2+2x+3与x轴的交点为A(-1,0),B(3,0),把抛物线y=
-x2+2x+3在x轴上方的部分沿x轴翻折到x轴下方,则翻折部分的抛物线解析式为y=(x-1)2-4(-1
当直线y=x+b与抛物线y=(x-1)2-4(-1
令y=0得x=-,
∴此时函数y=(4a+2)x2+(9-6a)x-4a+4(实数a为常数)的图象与x轴有交点;
当4a+2≠0,即a≠-时,y=(4a+2)x2+(9-6a)x-4a+4为二次函数,
∵Δ=(9-6a)2-4(4a+2)(-4a+4)=100a2-140a+49=(10a-7)2≥0,
∴函数y=(4a+2)x2+(9-6a)x-4a+4(实数a为常数)的图象与x轴有交点.
综上所述,无论a取何实数,图象T与x轴总有公共点.
(2)存在整数a,使图象T与x轴的公共点中有整点.当a=-时,不符合题意;当a≠-时,在y=(4a+2)x2+(9-6a)x-4a+4中,令y=0得0=(4a+2)x2+(9-6a)x-4a+4,解得x=-或x=,a是整数,∴当2a+1是6的因数时,是整数,∴2a+1=-6或2a+1=-3或2a+1=-2或2a+1=-1或2a+1=1或2a+1=2或2a+1=3或2a+1=6,解得a=-或a=-2或a=-或a=-1或a=0或a=或a=1或a=,∵a是整数,∴a=-2或a=-1或a=0或a=1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
