2024北师大版数学九年级下学期课时练--3.5 确定圆的条件同步练习(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--3.5 确定圆的条件同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 17:34:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
第三章 圆
5 确定圆的条件
基础过关全练
知识点1 确定圆的条件
1.下列说法错误的是( )
A.已知圆心和半径可以作一个圆
B.经过一个已知点A的圆能作无数个
C.经过两个已知点A,B的圆能作两个
D.经过不在同一直线上的三个点A,B,C只能作一个圆
2.(2023江西中考)如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为( )
A.3 B.4 C.5 D.6
3.如图,要把残破的圆片复制完整.已知弧上的三点A,B,C,用尺规作图找出所在圆的圆心(保留作图痕迹).
知识点2 三角形的外接圆及三角形的外心
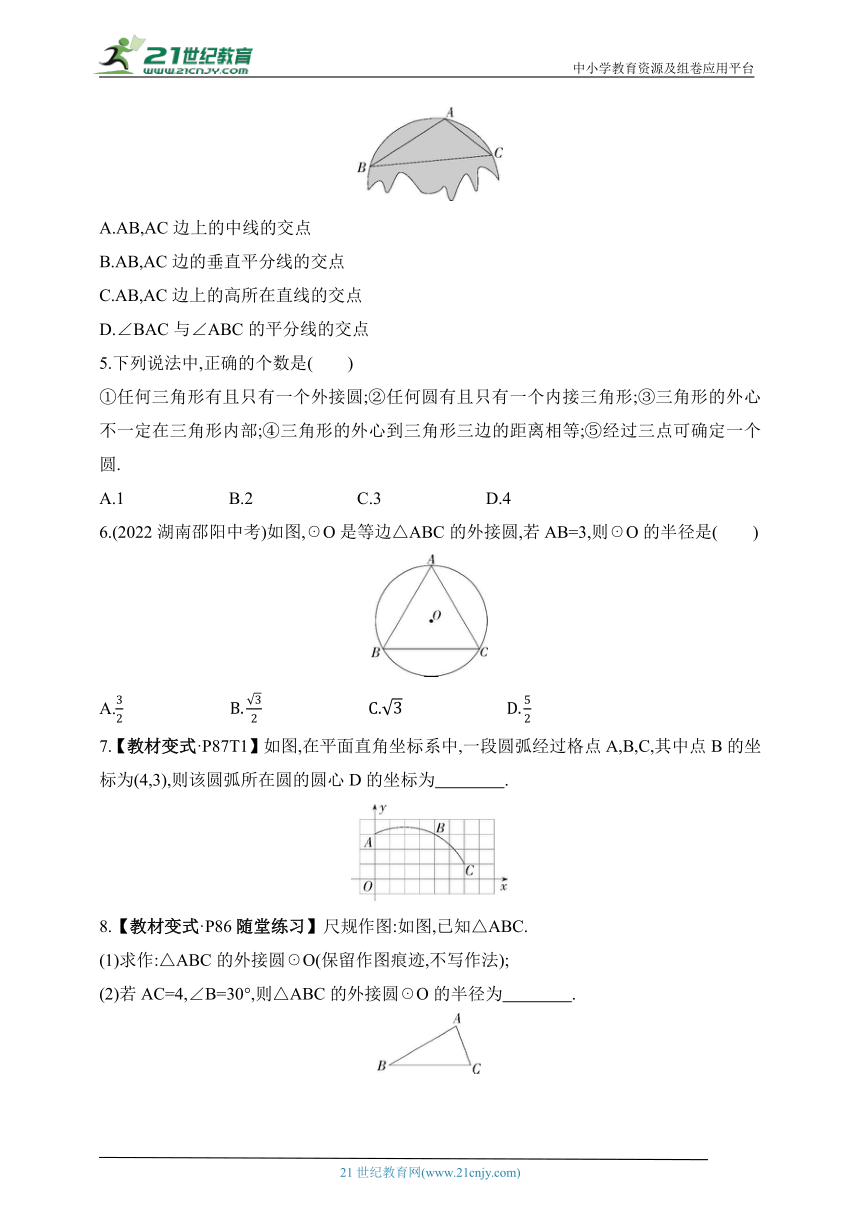
4.小红不小心把家里的一块圆形玻璃镜打碎了,需要配一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )
A.AB,AC边上的中线的交点
B.AB,AC边的垂直平分线的交点
C.AB,AC边上的高所在直线的交点
D.∠BAC与∠ABC的平分线的交点
5.下列说法中,正确的个数是( )
①任何三角形有且只有一个外接圆;②任何圆有且只有一个内接三角形;③三角形的外心不一定在三角形内部;④三角形的外心到三角形三边的距离相等;⑤经过三点可确定一个圆.
A.1 B.2 C.3 D.4
6.(2022湖南邵阳中考)如图,☉O是等边△ABC的外接圆,若AB=3,则☉O的半径是( )
A.
7.【教材变式·P87T1】如图,在平面直角坐标系中,一段圆弧经过格点A,B,C,其中点B的坐标为(4,3),则该圆弧所在圆的圆心D的坐标为 .
8.【教材变式·P86随堂练习】尺规作图:如图,已知△ABC.
(1)求作:△ABC的外接圆☉O(保留作图痕迹,不写作法);
(2)若AC=4,∠B=30°,则△ABC的外接圆☉O的半径为 .
能力提升全练
9.(2023台湾省中考,17,★★☆)如图所示的方格纸中,每个方格的边长为1,A、O两点皆在格线的交点上,今在此方格纸格线的交点上另外找两点B、C,使得△ABC的外心为O,则BC的长度为( )
A.4 B.5 C.
10.【新考向·尺规作图】(2023内蒙古通辽中考,10,★★☆)下面是“作已知直角三角形的外接圆”的尺规作图过程:
已知:如图1,在Rt△ABC中,∠C=90°.
求作:Rt△ABC的外接圆.
图1 图2
作法:如图2,
(1)分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于P,Q两点;
(2)作直线PQ,交AB于点O;
(3)以O为圆心,OA长为半径作☉O.
☉O即为所求作的圆.
下列不属于该尺规作图依据的是( )
A.两点确定一条直线
B.直角三角形斜边上的中线等于斜边的一半
C.与线段两个端点距离相等的点在这条线段的垂直平分线上
D.线段垂直平分线上的点与这条线段两个端点的距离相等
11.(2022广西玉林中考,17,★★☆)如图所示,在5×7的网格中,各个小正方形的边长均为1,点O,A,B,C,D,E均在格点处,点O是△ABC的外心,在不添加其他字母的情况下,把你认为外心也是O的三角形(△ABC除外)都写出来: .
素养探究全练
12.【推理能力】(2020四川凉山州中考)如图,☉O的半径为R,其内接锐角三角形ABC中,∠A、∠B、∠C所对的边分别是a、b、c.
(1)求证:=2R;
(2)若∠A=60°,∠C=45°,BC=4,利用(1)中的结论求AB的长和sin B的值.
答案全解全析
基础过关全练
1.C 经过两个已知点A,B的圆能作无数个,C中说法错误.故选C.
2.D 根据“经过不在同一直线上的三点确定一个圆”得,经过A、B、P或A、C、P或A、D、P或B、C、P或B、D、P或C、D、P可以确定圆,故最多可画出圆的个数为6,故选D.
3.解析 如图,连接AB,BC,分别作AB,BC的垂直平分线,两条垂直平分线的交点即为所求圆的圆心.
4.B 由题意可得,所求的圆形玻璃镜是△ABC的外接圆,∴这块玻璃镜的圆心是△ABC三边垂直平分线的交点,故选B.
5.B ①③正确.任何一个圆都有无数个内接三角形,故②错误;三角形的外心到三角形的三个顶点的距离相等,故④错误;经过不在同一直线上的三点可确定一个圆,故⑤错误.故选B.
6.C 作直径AD,连接CD,如图,
∵△ABC为等边三角形,∴AC=AB=3,∠B=60°,
∵AD为直径,∴∠ACD=90°,
∵∠D=∠B=60°,∴∠DAC=30°,∴CD=
(舍负),
∴OA=,即☉O的半径为.故选C.
7.(2,-1)
解析 连接AB,BC,作AB和BC的垂直平分线,它们相交于点D,点D即为圆心,如图,则圆心D的坐标为(2,-1).
8.解析 (1)如图所示,☉O即为所求作的圆.
(2)如图,连接OA,OC,
∵∠B=30°,∴∠AOC=60°,
又∵OA=OC,
∴△OAC为等边三角形,
∴OA=OC=AC=4,
∴△ABC的外接圆☉O的半径为4.
能力提升全练
9.D 由三角形外心的性质“三角形的外心到三角形三个顶点的距离相等”得到OB=OC=OA,从而确定B、C的位置(如图).
∴BC=.故选D.
10.D (2)的依据是“两点确定一条直线”;(1)的依据是“与线段两个端点距离相等的点在这条线段的垂直平分线上”;(3)的依据是“直角三角形斜边上的中线等于斜边的一半”.故选D.
11.△ABD,△ACD,△BCD
解析 由题图可知OA=,
∴OA=OB=OC=OD≠OE,
∴除△ABC外,△ABD,△ACD,△BCD的外心都是点O,
故答案为△ABD,△ACD,△BCD.
素养探究全练
12.解析 (1)证明:作直径BE,连接CE,如图所示,
则∠BCE=90°,∠E=∠A,
∴sin A=sin E==2R,
同理=2R,
∴=2R.
(2)由(1)得=2R,即=2R,
∴AB==8,
如图,过点B作BH⊥AC于H,
∴∠AHB=∠BHC=90°,
∴AH=AB·cos 60°=4,
CH=BC·cos 45°=,
∴AC=AH+CH=2(),
∴sin∠ABC=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
第三章 圆
5 确定圆的条件
基础过关全练
知识点1 确定圆的条件
1.下列说法错误的是( )
A.已知圆心和半径可以作一个圆
B.经过一个已知点A的圆能作无数个
C.经过两个已知点A,B的圆能作两个
D.经过不在同一直线上的三个点A,B,C只能作一个圆
2.(2023江西中考)如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为( )
A.3 B.4 C.5 D.6
3.如图,要把残破的圆片复制完整.已知弧上的三点A,B,C,用尺规作图找出所在圆的圆心(保留作图痕迹).
知识点2 三角形的外接圆及三角形的外心
4.小红不小心把家里的一块圆形玻璃镜打碎了,需要配一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )
A.AB,AC边上的中线的交点
B.AB,AC边的垂直平分线的交点
C.AB,AC边上的高所在直线的交点
D.∠BAC与∠ABC的平分线的交点
5.下列说法中,正确的个数是( )
①任何三角形有且只有一个外接圆;②任何圆有且只有一个内接三角形;③三角形的外心不一定在三角形内部;④三角形的外心到三角形三边的距离相等;⑤经过三点可确定一个圆.
A.1 B.2 C.3 D.4
6.(2022湖南邵阳中考)如图,☉O是等边△ABC的外接圆,若AB=3,则☉O的半径是( )
A.
7.【教材变式·P87T1】如图,在平面直角坐标系中,一段圆弧经过格点A,B,C,其中点B的坐标为(4,3),则该圆弧所在圆的圆心D的坐标为 .
8.【教材变式·P86随堂练习】尺规作图:如图,已知△ABC.
(1)求作:△ABC的外接圆☉O(保留作图痕迹,不写作法);
(2)若AC=4,∠B=30°,则△ABC的外接圆☉O的半径为 .
能力提升全练
9.(2023台湾省中考,17,★★☆)如图所示的方格纸中,每个方格的边长为1,A、O两点皆在格线的交点上,今在此方格纸格线的交点上另外找两点B、C,使得△ABC的外心为O,则BC的长度为( )
A.4 B.5 C.
10.【新考向·尺规作图】(2023内蒙古通辽中考,10,★★☆)下面是“作已知直角三角形的外接圆”的尺规作图过程:
已知:如图1,在Rt△ABC中,∠C=90°.
求作:Rt△ABC的外接圆.
图1 图2
作法:如图2,
(1)分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于P,Q两点;
(2)作直线PQ,交AB于点O;
(3)以O为圆心,OA长为半径作☉O.
☉O即为所求作的圆.
下列不属于该尺规作图依据的是( )
A.两点确定一条直线
B.直角三角形斜边上的中线等于斜边的一半
C.与线段两个端点距离相等的点在这条线段的垂直平分线上
D.线段垂直平分线上的点与这条线段两个端点的距离相等
11.(2022广西玉林中考,17,★★☆)如图所示,在5×7的网格中,各个小正方形的边长均为1,点O,A,B,C,D,E均在格点处,点O是△ABC的外心,在不添加其他字母的情况下,把你认为外心也是O的三角形(△ABC除外)都写出来: .
素养探究全练
12.【推理能力】(2020四川凉山州中考)如图,☉O的半径为R,其内接锐角三角形ABC中,∠A、∠B、∠C所对的边分别是a、b、c.
(1)求证:=2R;
(2)若∠A=60°,∠C=45°,BC=4,利用(1)中的结论求AB的长和sin B的值.
答案全解全析
基础过关全练
1.C 经过两个已知点A,B的圆能作无数个,C中说法错误.故选C.
2.D 根据“经过不在同一直线上的三点确定一个圆”得,经过A、B、P或A、C、P或A、D、P或B、C、P或B、D、P或C、D、P可以确定圆,故最多可画出圆的个数为6,故选D.
3.解析 如图,连接AB,BC,分别作AB,BC的垂直平分线,两条垂直平分线的交点即为所求圆的圆心.
4.B 由题意可得,所求的圆形玻璃镜是△ABC的外接圆,∴这块玻璃镜的圆心是△ABC三边垂直平分线的交点,故选B.
5.B ①③正确.任何一个圆都有无数个内接三角形,故②错误;三角形的外心到三角形的三个顶点的距离相等,故④错误;经过不在同一直线上的三点可确定一个圆,故⑤错误.故选B.
6.C 作直径AD,连接CD,如图,
∵△ABC为等边三角形,∴AC=AB=3,∠B=60°,
∵AD为直径,∴∠ACD=90°,
∵∠D=∠B=60°,∴∠DAC=30°,∴CD=
(舍负),
∴OA=,即☉O的半径为.故选C.
7.(2,-1)
解析 连接AB,BC,作AB和BC的垂直平分线,它们相交于点D,点D即为圆心,如图,则圆心D的坐标为(2,-1).
8.解析 (1)如图所示,☉O即为所求作的圆.
(2)如图,连接OA,OC,
∵∠B=30°,∴∠AOC=60°,
又∵OA=OC,
∴△OAC为等边三角形,
∴OA=OC=AC=4,
∴△ABC的外接圆☉O的半径为4.
能力提升全练
9.D 由三角形外心的性质“三角形的外心到三角形三个顶点的距离相等”得到OB=OC=OA,从而确定B、C的位置(如图).
∴BC=.故选D.
10.D (2)的依据是“两点确定一条直线”;(1)的依据是“与线段两个端点距离相等的点在这条线段的垂直平分线上”;(3)的依据是“直角三角形斜边上的中线等于斜边的一半”.故选D.
11.△ABD,△ACD,△BCD
解析 由题图可知OA=,
∴OA=OB=OC=OD≠OE,
∴除△ABC外,△ABD,△ACD,△BCD的外心都是点O,
故答案为△ABD,△ACD,△BCD.
素养探究全练
12.解析 (1)证明:作直径BE,连接CE,如图所示,
则∠BCE=90°,∠E=∠A,
∴sin A=sin E==2R,
同理=2R,
∴=2R.
(2)由(1)得=2R,即=2R,
∴AB==8,
如图,过点B作BH⊥AC于H,
∴∠AHB=∠BHC=90°,
∴AH=AB·cos 60°=4,
CH=BC·cos 45°=,
∴AC=AH+CH=2(),
∴sin∠ABC=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
