2024北师大版数学九年级下学期课时练--1.5 三角函数的应用同步练习(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--1.5 三角函数的应用同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 458.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 17:40:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
第一章 直角三角形的边角关系
5 三角函数的应用
基础过关全练
知识点1 方向角的定义及应用
1.(2023河北任丘模拟)如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,那么海轮航行的距离AB是 ( )
A.海里 B.2sin 55°海里 C.海里 D.2cos 55°海里
2.如图,在O点有一座5G移动信号塔,O点正北方向950 m处有一居民楼A,在A南偏东20°方向有一居民楼B.O,B之间有一个水塘,O点在B点的北偏西60°方向,有关资料表明信号塔与周边住户的安全距离是500 m,请你通过计算判断居民楼B是否安全.(参考数据:≈1.732,tan 70°≈2.747)
3.【国家安全】(2023河南商丘模拟)如图,一艘中国军舰在南海的A处正常巡逻,突然收到北偏东53°方向的C处的一艘中国远洋油轮的求救信号,同时,一艘巡逻艇在C处的南偏东30° 方向,距离C处40海里的B处也收到求救信号,巡逻艇在中国军舰的正东方向上,已知军舰的速度为30海里/小时,巡逻艇的速度为20海里/小时,若军舰和巡逻艇同时出发,哪个会先到达救援地点C处 (参考数据:sin 53°≈0.8,cos 53°≈0.6,tan 53°≈1.3,≈1.73)
知识点2 三角函数的应用
4.【教材变式·P19想一想】(2022四川眉山中考)数学实践活动小组去测量眉山市某标志性建筑物的高CD.如图,在楼前平地A处测得楼顶C处的仰角为30°,沿AD方向前进60 m到达B处,测得楼顶C处的仰角为45°,求此建筑物的高.(结果保留整数.参考数据:≈1.41,≈1.73)
5.(2022湖南株洲中考)如图1所示,某登山运动爱好者由山坡①的山顶点A处沿线段AC至山谷点C处,再从点C处沿线段CB至山坡②的山顶点B处.如图2所示,将直线l视为水平面,山坡①的坡角∠ACM=30°,其高度AM为0.6千米,山坡②的坡度i=1∶1,BN⊥l于N,且CN=千米.
(1)求∠ACB的度数;
(2)求在此过程中该登山运动爱好者走过的路程.
图1 图2
能力提升全练
6.【跨学科·体育与健康】(2023浙江绍兴中考,19,★★☆)图1是某款篮球架,图2是其示意图,立柱OA⊥地面OB,支架CD与OA交于点A,支架CG⊥CD交OA于点G,支架DE平行于地面OB,篮筐EF与支架DE在同一直线上,OA=2.5米,AD=0.8米,∠AGC=32°.
(1)求∠GAC的度数;
(2)某运动员准备给篮筐挂上篮网,如果他站在凳子上,最高可以把篮网挂到离地面3米处,那么他能挂上篮网吗 请通过计算说明理由.(参考数据:sin 32°≈0.53,cos 32°≈0.85,tan 32°≈0.62)
图1 图2
7.【真实情境】(2023安徽合肥高新区一模,19,★★☆)2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图所示的是处于工作状态的某型号手臂机器人示意图,OA是垂直于工作台的移动基座,AB、BC为机械臂,OA=1 m,AB=5 m,BC=2 m,∠ABC=
143°.机械臂端点C到工作台的距离CD=6 m.
(1)求A、C两点之间的距离;
(2)求OD的长.
(结果精确到0.1 m,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,
≈2.24)
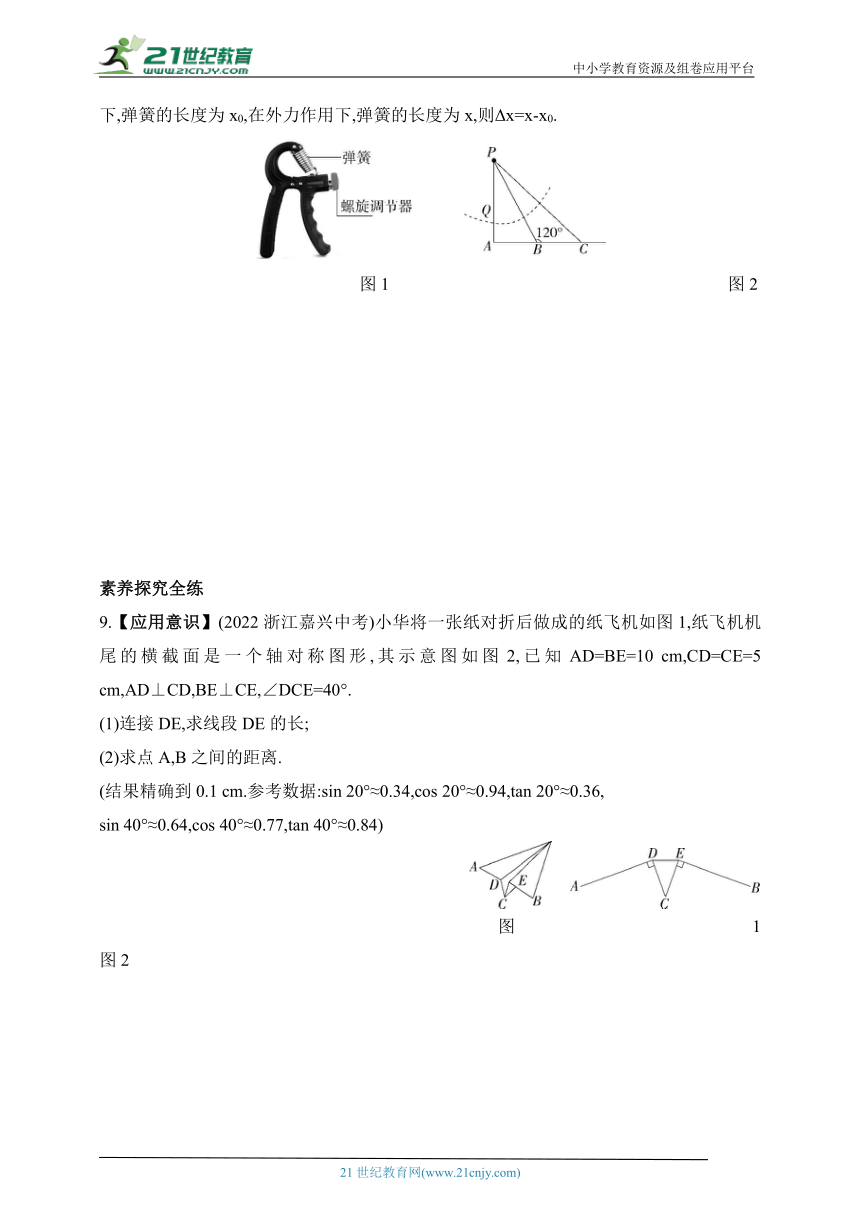
8.【跨学科·物理】(2022湖南娄底中考,22,★★☆)“体育承载着国家强盛、民族振兴的梦想”.墩墩使用握力器(如图1)锻炼手部肌肉.如图2,握力器弹簧的一端固定在点P处,在无外力作用下,弹簧的长度为3 cm,即PQ=3 cm.开始训练时,将弹簧的端点Q调在点B处,此时弹簧的长PB=4 cm,弹力大小是100 N,经过一段时间的锻炼后,他手部的力量大大提高,需增加训练强度,于是将弹簧端点Q调到C处,使弹力大小变为300 N,已知∠PBC=120°,求BC的长.
注:弹簧的弹力与形变成正比,即F=k·Δx,k是劲度系数,Δx是弹簧的形变量,在无外力作用下,弹簧的长度为x0,在外力作用下,弹簧的长度为x,则Δx=x-x0.
图1 图2
素养探究全练
9.【应用意识】(2022浙江嘉兴中考)小华将一张纸对折后做成的纸飞机如图1,纸飞机机尾的横截面是一个轴对称图形,其示意图如图2,已知AD=BE=10 cm,CD=CE=5 cm,AD⊥CD,BE⊥CE,∠DCE=40°.
(1)连接DE,求线段DE的长;
(2)求点A,B之间的距离.
(结果精确到0.1 cm.参考数据:sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36,
sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
图1 图2
答案全解全析
基础过关全练
1.D 由题意得AB⊥BP,NP∥AB,∠NPA=55°,∴∠A=∠NPA=55°,在Rt△APB中,AP=2海里,∴AB=AP·cos 55°=2cos 55°(海里),∴海轮航行的距离AB是2cos 55°海里,故选D.
2.解析 如图,作BC⊥AO,交AO的延长线于点C.
由题意可知∠A=20°,∠COB=∠OBD=60°,
则∠ABC=90°-20°=70°,∠OBC=30°.
设OC=x m,则OB=2x m,BC=x m,
∴AC=AO+OC=(950+x)m,
在Rt△ABC中,tan∠ABC=,
∴AC=BC·tan∠ABC=x·tan 70° m,
∴950+x=x·tan 70°,∴x=≈252.81,
则OB=2x≈505.6 m,
∵505.6>500,∴居民楼B是安全的.
3.解析 如图,过点C作CD⊥AB于点D,
由题意可知BC=40海里,∠ACD=53°,∠BCD=30°,
在Rt△BCD中,BC=40海里,∠BCD=30°,
∴CD=BC·cos 30°=40=60(海里),
在Rt△ACD中,CD=60海里,∠ACD=53°,
∴AC==100(海里),
∴军舰到达点C的时间为≈3.33(时).
巡逻艇到达点C的时间为≈3.46(时),
∵3.33<3.46,∴军舰先到达救援地点C处.
4.解析 在Rt△BCD中,∠CBD=45°,∴BD=CD.
设CD=x m,则BD=x m,
∴AD=BD+AB=(60+x)m,
在Rt△ACD中,
tan∠CAD=tan 30°=,
解得x=30+30≈82.
答:此建筑物的高约为82 m.
5.解析 (1)∵山坡②的坡度i=1∶1,
∴CN=BN,∴∠BCN=45°,
∴∠ACB=180°-30°-45°=105°.
(2)在Rt△ACM中,∠AMC=90°,∠ACM=30°,AM=0.6千米,
∴AC=2AM=1.2千米,
在Rt△BCN中,∠BNC=90°,∠BCN=45°,CN=千米,
则BC==2(千米),
1.2+2=3.2(千米).
答:该登山运动爱好者走过的路程为3.2千米.
能力提升全练
6.解析 (1)∵CG⊥CD,∴∠ACG=90°,
∵∠AGC=32°,∴∠GAC=90°-∠AGC=90°-32°=58°.
(2)该运动员能挂上篮网,理由如下:
延长OA,ED交于点M,如图,
∵OA⊥OB,∴∠AOB=90°,
∵DE∥OB,
∴∠DMA=∠AOB=90°,
∵∠GAC=58°,∴∠DAM=∠GAC=58°,
∴∠ADM=90°-∠DAM=32°,
在Rt△ADM中,AD=0.8米,
∴AM=AD·sin 32°≈0.8×0.53=0.424(米),
∴OM=OA+AM=2.5+0.424=2.924(米),
∵2.924米<3米,∴该运动员能挂上篮网.
7.解析 (1)如图,连接AC,过点A作AE⊥CB,垂足为E,
在Rt△ABE中,AB=5 m,∠ABE=180°-143°=37°,
∵sin∠ABE=,cos∠ABE=,
∴AE=AB·sin∠ABE≈5×0.60=3 m,
BE=AB·cos∠ABE≈5×0.80=4 m,
∴CE=BC+BE=2+4=6(m),
在Rt△ACE中,由勾股定理得AC=≈6.7 m.
故A、C两点之间的距离约为6.7 m.
(2)过点A作AF⊥CD,垂足为F,
∴FD=AO=1 m,∴CF=5 m,
在Rt△ACF中,由勾股定理得AF=(m).
∴OD=AF=2≈4.5 m,即OD的长约为4.5 m.
8.解析 由题意可得x0=3 cm,100=k(4-3),
解得k=100,∴F=100Δx,
当F=300 N时,300=100×(PC-3),解得PC=6 cm,
由题图可得∠PAB=90°,∠PBC=120°,
∴∠APB=30°,
∴AB=PB·sin∠APB=4×sin 30°=4×=2(cm),
PA=PB·cos∠APB=4×(cm),
∵PC=6 cm,
∴AC=(cm),
∴BC=AC-AB=(2-2)cm,
即BC的长是(2-2)cm.
素养探究全练
9.解析 (1)如图,过点C作CF⊥DE于点F,
∵CD=CE=5 cm,∠DCE=40°,∴∠DCF=20°,
∴DF=CD·sin 20°≈5×0.34=1.7(cm),
∴DE=2DF=3.4 cm,∴线段DE的长约为3.4 cm.
(2)延长CF交AD,BE的延长线于点G,连接AB,
∵横截面是一个轴对称图形,∴DE∥AB,∴∠A=∠GDE,
∵AD⊥CD,BE⊥CE,∴∠GDF+∠FDC=90°,
∵∠DCF+∠FDC=90°,∴∠GDF=∠DCF=20°,
∴∠A=20°,DG=≈1.81(cm),
∴AG=AD+DG=10+1.81=11.81(cm),
∴AB=2AG·cos 20°≈2×11.81×0.94≈22.2(cm).
∴点A,B之间的距离约为22.2 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
第一章 直角三角形的边角关系
5 三角函数的应用
基础过关全练
知识点1 方向角的定义及应用
1.(2023河北任丘模拟)如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,那么海轮航行的距离AB是 ( )
A.海里 B.2sin 55°海里 C.海里 D.2cos 55°海里
2.如图,在O点有一座5G移动信号塔,O点正北方向950 m处有一居民楼A,在A南偏东20°方向有一居民楼B.O,B之间有一个水塘,O点在B点的北偏西60°方向,有关资料表明信号塔与周边住户的安全距离是500 m,请你通过计算判断居民楼B是否安全.(参考数据:≈1.732,tan 70°≈2.747)
3.【国家安全】(2023河南商丘模拟)如图,一艘中国军舰在南海的A处正常巡逻,突然收到北偏东53°方向的C处的一艘中国远洋油轮的求救信号,同时,一艘巡逻艇在C处的南偏东30° 方向,距离C处40海里的B处也收到求救信号,巡逻艇在中国军舰的正东方向上,已知军舰的速度为30海里/小时,巡逻艇的速度为20海里/小时,若军舰和巡逻艇同时出发,哪个会先到达救援地点C处 (参考数据:sin 53°≈0.8,cos 53°≈0.6,tan 53°≈1.3,≈1.73)
知识点2 三角函数的应用
4.【教材变式·P19想一想】(2022四川眉山中考)数学实践活动小组去测量眉山市某标志性建筑物的高CD.如图,在楼前平地A处测得楼顶C处的仰角为30°,沿AD方向前进60 m到达B处,测得楼顶C处的仰角为45°,求此建筑物的高.(结果保留整数.参考数据:≈1.41,≈1.73)
5.(2022湖南株洲中考)如图1所示,某登山运动爱好者由山坡①的山顶点A处沿线段AC至山谷点C处,再从点C处沿线段CB至山坡②的山顶点B处.如图2所示,将直线l视为水平面,山坡①的坡角∠ACM=30°,其高度AM为0.6千米,山坡②的坡度i=1∶1,BN⊥l于N,且CN=千米.
(1)求∠ACB的度数;
(2)求在此过程中该登山运动爱好者走过的路程.
图1 图2
能力提升全练
6.【跨学科·体育与健康】(2023浙江绍兴中考,19,★★☆)图1是某款篮球架,图2是其示意图,立柱OA⊥地面OB,支架CD与OA交于点A,支架CG⊥CD交OA于点G,支架DE平行于地面OB,篮筐EF与支架DE在同一直线上,OA=2.5米,AD=0.8米,∠AGC=32°.
(1)求∠GAC的度数;
(2)某运动员准备给篮筐挂上篮网,如果他站在凳子上,最高可以把篮网挂到离地面3米处,那么他能挂上篮网吗 请通过计算说明理由.(参考数据:sin 32°≈0.53,cos 32°≈0.85,tan 32°≈0.62)
图1 图2
7.【真实情境】(2023安徽合肥高新区一模,19,★★☆)2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图所示的是处于工作状态的某型号手臂机器人示意图,OA是垂直于工作台的移动基座,AB、BC为机械臂,OA=1 m,AB=5 m,BC=2 m,∠ABC=
143°.机械臂端点C到工作台的距离CD=6 m.
(1)求A、C两点之间的距离;
(2)求OD的长.
(结果精确到0.1 m,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,
≈2.24)
8.【跨学科·物理】(2022湖南娄底中考,22,★★☆)“体育承载着国家强盛、民族振兴的梦想”.墩墩使用握力器(如图1)锻炼手部肌肉.如图2,握力器弹簧的一端固定在点P处,在无外力作用下,弹簧的长度为3 cm,即PQ=3 cm.开始训练时,将弹簧的端点Q调在点B处,此时弹簧的长PB=4 cm,弹力大小是100 N,经过一段时间的锻炼后,他手部的力量大大提高,需增加训练强度,于是将弹簧端点Q调到C处,使弹力大小变为300 N,已知∠PBC=120°,求BC的长.
注:弹簧的弹力与形变成正比,即F=k·Δx,k是劲度系数,Δx是弹簧的形变量,在无外力作用下,弹簧的长度为x0,在外力作用下,弹簧的长度为x,则Δx=x-x0.
图1 图2
素养探究全练
9.【应用意识】(2022浙江嘉兴中考)小华将一张纸对折后做成的纸飞机如图1,纸飞机机尾的横截面是一个轴对称图形,其示意图如图2,已知AD=BE=10 cm,CD=CE=5 cm,AD⊥CD,BE⊥CE,∠DCE=40°.
(1)连接DE,求线段DE的长;
(2)求点A,B之间的距离.
(结果精确到0.1 cm.参考数据:sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36,
sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
图1 图2
答案全解全析
基础过关全练
1.D 由题意得AB⊥BP,NP∥AB,∠NPA=55°,∴∠A=∠NPA=55°,在Rt△APB中,AP=2海里,∴AB=AP·cos 55°=2cos 55°(海里),∴海轮航行的距离AB是2cos 55°海里,故选D.
2.解析 如图,作BC⊥AO,交AO的延长线于点C.
由题意可知∠A=20°,∠COB=∠OBD=60°,
则∠ABC=90°-20°=70°,∠OBC=30°.
设OC=x m,则OB=2x m,BC=x m,
∴AC=AO+OC=(950+x)m,
在Rt△ABC中,tan∠ABC=,
∴AC=BC·tan∠ABC=x·tan 70° m,
∴950+x=x·tan 70°,∴x=≈252.81,
则OB=2x≈505.6 m,
∵505.6>500,∴居民楼B是安全的.
3.解析 如图,过点C作CD⊥AB于点D,
由题意可知BC=40海里,∠ACD=53°,∠BCD=30°,
在Rt△BCD中,BC=40海里,∠BCD=30°,
∴CD=BC·cos 30°=40=60(海里),
在Rt△ACD中,CD=60海里,∠ACD=53°,
∴AC==100(海里),
∴军舰到达点C的时间为≈3.33(时).
巡逻艇到达点C的时间为≈3.46(时),
∵3.33<3.46,∴军舰先到达救援地点C处.
4.解析 在Rt△BCD中,∠CBD=45°,∴BD=CD.
设CD=x m,则BD=x m,
∴AD=BD+AB=(60+x)m,
在Rt△ACD中,
tan∠CAD=tan 30°=,
解得x=30+30≈82.
答:此建筑物的高约为82 m.
5.解析 (1)∵山坡②的坡度i=1∶1,
∴CN=BN,∴∠BCN=45°,
∴∠ACB=180°-30°-45°=105°.
(2)在Rt△ACM中,∠AMC=90°,∠ACM=30°,AM=0.6千米,
∴AC=2AM=1.2千米,
在Rt△BCN中,∠BNC=90°,∠BCN=45°,CN=千米,
则BC==2(千米),
1.2+2=3.2(千米).
答:该登山运动爱好者走过的路程为3.2千米.
能力提升全练
6.解析 (1)∵CG⊥CD,∴∠ACG=90°,
∵∠AGC=32°,∴∠GAC=90°-∠AGC=90°-32°=58°.
(2)该运动员能挂上篮网,理由如下:
延长OA,ED交于点M,如图,
∵OA⊥OB,∴∠AOB=90°,
∵DE∥OB,
∴∠DMA=∠AOB=90°,
∵∠GAC=58°,∴∠DAM=∠GAC=58°,
∴∠ADM=90°-∠DAM=32°,
在Rt△ADM中,AD=0.8米,
∴AM=AD·sin 32°≈0.8×0.53=0.424(米),
∴OM=OA+AM=2.5+0.424=2.924(米),
∵2.924米<3米,∴该运动员能挂上篮网.
7.解析 (1)如图,连接AC,过点A作AE⊥CB,垂足为E,
在Rt△ABE中,AB=5 m,∠ABE=180°-143°=37°,
∵sin∠ABE=,cos∠ABE=,
∴AE=AB·sin∠ABE≈5×0.60=3 m,
BE=AB·cos∠ABE≈5×0.80=4 m,
∴CE=BC+BE=2+4=6(m),
在Rt△ACE中,由勾股定理得AC=≈6.7 m.
故A、C两点之间的距离约为6.7 m.
(2)过点A作AF⊥CD,垂足为F,
∴FD=AO=1 m,∴CF=5 m,
在Rt△ACF中,由勾股定理得AF=(m).
∴OD=AF=2≈4.5 m,即OD的长约为4.5 m.
8.解析 由题意可得x0=3 cm,100=k(4-3),
解得k=100,∴F=100Δx,
当F=300 N时,300=100×(PC-3),解得PC=6 cm,
由题图可得∠PAB=90°,∠PBC=120°,
∴∠APB=30°,
∴AB=PB·sin∠APB=4×sin 30°=4×=2(cm),
PA=PB·cos∠APB=4×(cm),
∵PC=6 cm,
∴AC=(cm),
∴BC=AC-AB=(2-2)cm,
即BC的长是(2-2)cm.
素养探究全练
9.解析 (1)如图,过点C作CF⊥DE于点F,
∵CD=CE=5 cm,∠DCE=40°,∴∠DCF=20°,
∴DF=CD·sin 20°≈5×0.34=1.7(cm),
∴DE=2DF=3.4 cm,∴线段DE的长约为3.4 cm.
(2)延长CF交AD,BE的延长线于点G,连接AB,
∵横截面是一个轴对称图形,∴DE∥AB,∴∠A=∠GDE,
∵AD⊥CD,BE⊥CE,∴∠GDF+∠FDC=90°,
∵∠DCF+∠FDC=90°,∴∠GDF=∠DCF=20°,
∴∠A=20°,DG=≈1.81(cm),
∴AG=AD+DG=10+1.81=11.81(cm),
∴AB=2AG·cos 20°≈2×11.81×0.94≈22.2(cm).
∴点A,B之间的距离约为22.2 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
