2024北师大版数学九年级下学期课时练--3.8 圆内接正多边形同步练习(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--3.8 圆内接正多边形同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 534.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 17:44:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
第三章 圆
8 圆内接正多边形
基础过关全练
知识点1 圆内接正多边形
1.下列说法错误的是( )
A.圆内接正多边形每个内角都相等
B.圆内接正多边形都是轴对称图形
C.圆内接正多边形都是中心对称图形
D.圆内接正多边形的中心到各边的距离相等
2.(2023安徽中考)如图,正五边形ABCDE内接于☉O,连接OC,OD,则∠BAE-∠COD=( )
A.60° B.54° C.48° D.36°
3.图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形面板翻折起来后,就能形成一个圆形桌面(可近似看做正方形的外接圆),正方形桌面与翻折成的圆形桌面的面积之比最接近( )
A.
4.如图,将一个小正方形EFGH和4个全等的直角三角形拼成一个大正方形ABCD,已知每一个直角三角形的两直角边长分别是a、b,正方形ABCD的内切圆半径为R,正方形EFGH的外接圆半径为r,下列说法不正确的是( )
A.正方形ABCD的内切圆与正方形EFGH的外接圆是同心圆
B.R=r
C.R≤r
D.R∶r=(a+b)∶
知识点2 圆内接正多边形的画法
5.已知☉O和☉O上一点A.
(1)作☉O的内接正方形ABCD和内接正六边形AEFCGH(点E在上);
(2)在(1)所作的图中,求证:DE是☉O的内接正十二边形的一边.
能力提升全练
6.(2020四川凉山州中考,11,★★☆)如图,等边三角形ABC和正方形ADEF都内接于☉O,则AD∶AB=( )
A.2 C.
7.(2023河北中考,9,★★☆)如图,点P1~P8是☉O的八等分点.若△P1P3P7,四边形P3P4P6P7的周长分别为a,b,则下列正确的是( )
A.ab D.a,b大小无法比较
8.【数学文化】(2023福建中考,10,★★☆)我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣.”“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.141 6.如图,☉O的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计☉O的面积,可得π的估计值为,若用圆内接正十二边形作近似估计,可得π的估计值为( )
A.
9.(2023湖南衡阳中考,18,★★☆)如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是
10.(2021广东珠海香洲期末,17,★★☆)如图,已知AB是☉O的直径,若CD是☉O内接正n边形的一边,AD是☉O内接正(n+4)边形的一边,BD=AC,则n= .
11.(2022浙江金华中考,22,★★☆)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答下列问题.作法:如图2,①作直径AF.②以F为圆心,FO长为半径作圆弧,与☉O交于点M,N.③连接AM,MN,NA.
(1)求∠ABC的度数.
(2)△AMN是正三角形吗 请说明理由.
(3)从点A开始,以DN长为半径,在☉O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
图1 图2
素养探究全练
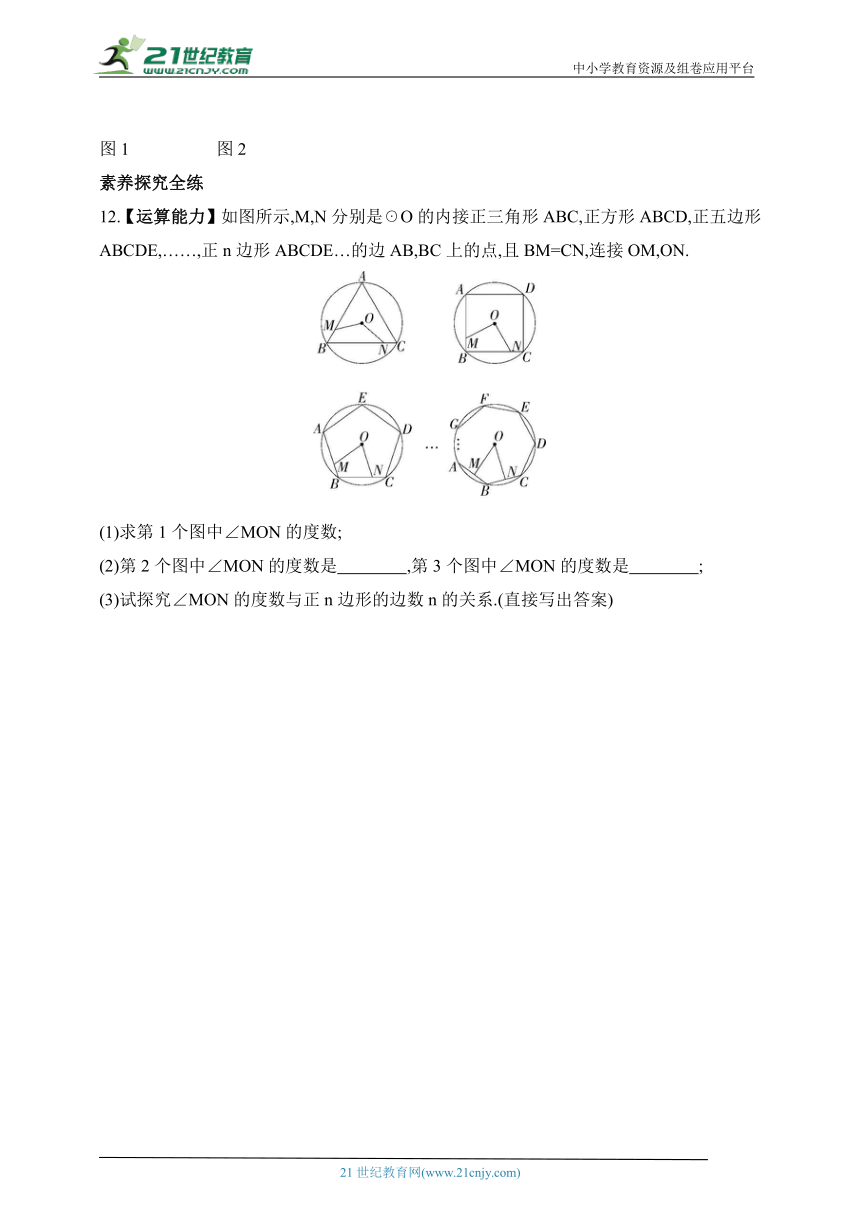
12.【运算能力】如图所示,M,N分别是☉O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,……,正n边形ABCDE…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求第1个图中∠MON的度数;
(2)第2个图中∠MON的度数是 ,第3个图中∠MON的度数是 ;
(3)试探究∠MON的度数与正n边形的边数n的关系.(直接写出答案)
答案全解全析
基础过关全练
1.C 根据圆内接正多边形的性质,可得A、B、D说法正确;若圆内接正多边形的边数为奇数,则它不是中心对称图形,故C说法错误.故选C.
2.D ∵五边形ABCDE是正五边形,∴∠BAE==108°,
∠COD==72°,∴∠BAE-∠COD=108°-72°=36°,故选D.
3.C 如图,连接AC,设正方形的边长为a,∵四边形ABCD是正方形,∴∠B=90°,∴AC为圆的直径,AC=a,则正方形桌面与翻折成的圆形桌面的面积之比为,故选C.
4.B 如图,连接HF、GE,交于点O,易知正方形ABCD的内切圆和正方形EFGH的外接圆的圆心都为O,∴两个圆是同心圆,故A正确;易知R=≤0,∴R2≤r2,∴R≤r,故C、D正确,B不正确.故选B.
5.解析 (1)作图如图.
作法:①作直径AC;
②作直径BD⊥AC,依次连接AB、BC、CD、DA,
则四边形ABCD为☉O的内接正方形;
③分别以点A、C为圆心,OA长为半径画弧,交☉O于点E、H、F、G,顺次连接AE、EF、FC、CG、GH、HA,则六边形AEFCGH为☉O的内接正六边形.
(2)证明:如图,连接OE、DE.
∵∠AOD==90°,∠AOE==60°,
∴∠EOD=∠AOD-∠AOE=90°-60°=30°.
∵360°÷30°=12,
∴DE为☉O的内接正十二边形的一边.
能力提升全练
6.B 连接OA、OB、OD,过O作OH⊥AB于H,如图,
则AH=BH=AB,
∵正方形ADEF和等边三角形ABC都内接于☉O,
∴∠AOB=120°,∠AOD=90°,
∵AO=DO,∴AD=OA,
∵OA=OB,∴∠AOH=∠BOH=×120°=60°,
∴AH=OA·sin 60°=OA,
∴AB=2AH=2×OA,
∴,即AD∶AB=.故选B.
7.A 连接P4P5,P5P6.
∵点P1~P8是☉O的八等分点,
∴P3P4=P4P5=P5P6=P6P7,P1P7=P1P3=P4P6,
∴b-a=P3P4+P7P6-P1P3,
∵P5P4+P5P6>P4P6,
∴P3P4+P7P6>P1P3,
∴b-a>0,∴a8.C 如图,AB是正十二边形的一条边,点O是正十二边形的中心,过A作AM⊥OB于M,∵∠AOB=360°÷12=30°,∴AM=,
∴S△AOB=OB·AM=,∴正十二边形的面积为12×=3,
∴3≈12×π,∴π≈3,∴π的近似值为3,故选C.
9.10
解析 ∵多边形是正五边形,正五边形的每一个内角为×180°×(5-2)=108°,∴∠O=180°-(180°-108°)×2=36°,∴正五边形的个数是360°÷36°=10.故答案为10.
10.4
解析 连接OD,OC,∵BD=AC,∴,∴∠AOD=
∠BOC,∵∠AOD=∠BOC=,∠DOC=,AB为☉O的直径,
∴2×=180°.解得n=4或n=-2(舍),故答案为4.
11.解析 (1)∵五边形ABCDE是正五边形,
∴∠ABC==108°.
(2)△AMN是正三角形.理由:如图,连接ON,NF,由题意可得FN=OF=ON,∴△FON是等边三角形,∴∠NFA=60°,∴∠NMA=60°,
同理可得∠ANM=60°,∴∠MAN=60°,∴△MAN是正三角形.
(3)∵∠AMN=60°,∴∠AON=120°,
连接OD,则∠AOD=×2=144°,
∴∠NOD=∠AOD-∠AON=144°-120°=24°,
∵360°÷24°=15,∴n的值是15.
素养探究全练
12.解析 (1)如图所示,连接OB,OC,
∵△ABC为正三角形,
∴∠ABC=60°,∠BOC=120°,
∵OC=OB,
∴∠OBC=∠OCB=30°,
∴∠OBM=60°-30°=30°,
∴∠OBM=∠OCN,
又∵BM=CN,OB=OC,∴△OMB≌△ONC,
∴∠BOM=∠CON,∴∠MON=∠BOC=120°.
(2)90°;72°.
(3)∠MON=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
第三章 圆
8 圆内接正多边形
基础过关全练
知识点1 圆内接正多边形
1.下列说法错误的是( )
A.圆内接正多边形每个内角都相等
B.圆内接正多边形都是轴对称图形
C.圆内接正多边形都是中心对称图形
D.圆内接正多边形的中心到各边的距离相等
2.(2023安徽中考)如图,正五边形ABCDE内接于☉O,连接OC,OD,则∠BAE-∠COD=( )
A.60° B.54° C.48° D.36°
3.图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形面板翻折起来后,就能形成一个圆形桌面(可近似看做正方形的外接圆),正方形桌面与翻折成的圆形桌面的面积之比最接近( )
A.
4.如图,将一个小正方形EFGH和4个全等的直角三角形拼成一个大正方形ABCD,已知每一个直角三角形的两直角边长分别是a、b,正方形ABCD的内切圆半径为R,正方形EFGH的外接圆半径为r,下列说法不正确的是( )
A.正方形ABCD的内切圆与正方形EFGH的外接圆是同心圆
B.R=r
C.R≤r
D.R∶r=(a+b)∶
知识点2 圆内接正多边形的画法
5.已知☉O和☉O上一点A.
(1)作☉O的内接正方形ABCD和内接正六边形AEFCGH(点E在上);
(2)在(1)所作的图中,求证:DE是☉O的内接正十二边形的一边.
能力提升全练
6.(2020四川凉山州中考,11,★★☆)如图,等边三角形ABC和正方形ADEF都内接于☉O,则AD∶AB=( )
A.2 C.
7.(2023河北中考,9,★★☆)如图,点P1~P8是☉O的八等分点.若△P1P3P7,四边形P3P4P6P7的周长分别为a,b,则下列正确的是( )
A.a
8.【数学文化】(2023福建中考,10,★★☆)我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣.”“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.141 6.如图,☉O的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计☉O的面积,可得π的估计值为,若用圆内接正十二边形作近似估计,可得π的估计值为( )
A.
9.(2023湖南衡阳中考,18,★★☆)如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是
10.(2021广东珠海香洲期末,17,★★☆)如图,已知AB是☉O的直径,若CD是☉O内接正n边形的一边,AD是☉O内接正(n+4)边形的一边,BD=AC,则n= .
11.(2022浙江金华中考,22,★★☆)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答下列问题.作法:如图2,①作直径AF.②以F为圆心,FO长为半径作圆弧,与☉O交于点M,N.③连接AM,MN,NA.
(1)求∠ABC的度数.
(2)△AMN是正三角形吗 请说明理由.
(3)从点A开始,以DN长为半径,在☉O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
图1 图2
素养探究全练
12.【运算能力】如图所示,M,N分别是☉O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,……,正n边形ABCDE…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求第1个图中∠MON的度数;
(2)第2个图中∠MON的度数是 ,第3个图中∠MON的度数是 ;
(3)试探究∠MON的度数与正n边形的边数n的关系.(直接写出答案)
答案全解全析
基础过关全练
1.C 根据圆内接正多边形的性质,可得A、B、D说法正确;若圆内接正多边形的边数为奇数,则它不是中心对称图形,故C说法错误.故选C.
2.D ∵五边形ABCDE是正五边形,∴∠BAE==108°,
∠COD==72°,∴∠BAE-∠COD=108°-72°=36°,故选D.
3.C 如图,连接AC,设正方形的边长为a,∵四边形ABCD是正方形,∴∠B=90°,∴AC为圆的直径,AC=a,则正方形桌面与翻折成的圆形桌面的面积之比为,故选C.
4.B 如图,连接HF、GE,交于点O,易知正方形ABCD的内切圆和正方形EFGH的外接圆的圆心都为O,∴两个圆是同心圆,故A正确;易知R=≤0,∴R2≤r2,∴R≤r,故C、D正确,B不正确.故选B.
5.解析 (1)作图如图.
作法:①作直径AC;
②作直径BD⊥AC,依次连接AB、BC、CD、DA,
则四边形ABCD为☉O的内接正方形;
③分别以点A、C为圆心,OA长为半径画弧,交☉O于点E、H、F、G,顺次连接AE、EF、FC、CG、GH、HA,则六边形AEFCGH为☉O的内接正六边形.
(2)证明:如图,连接OE、DE.
∵∠AOD==90°,∠AOE==60°,
∴∠EOD=∠AOD-∠AOE=90°-60°=30°.
∵360°÷30°=12,
∴DE为☉O的内接正十二边形的一边.
能力提升全练
6.B 连接OA、OB、OD,过O作OH⊥AB于H,如图,
则AH=BH=AB,
∵正方形ADEF和等边三角形ABC都内接于☉O,
∴∠AOB=120°,∠AOD=90°,
∵AO=DO,∴AD=OA,
∵OA=OB,∴∠AOH=∠BOH=×120°=60°,
∴AH=OA·sin 60°=OA,
∴AB=2AH=2×OA,
∴,即AD∶AB=.故选B.
7.A 连接P4P5,P5P6.
∵点P1~P8是☉O的八等分点,
∴P3P4=P4P5=P5P6=P6P7,P1P7=P1P3=P4P6,
∴b-a=P3P4+P7P6-P1P3,
∵P5P4+P5P6>P4P6,
∴P3P4+P7P6>P1P3,
∴b-a>0,∴a
∴S△AOB=OB·AM=,∴正十二边形的面积为12×=3,
∴3≈12×π,∴π≈3,∴π的近似值为3,故选C.
9.10
解析 ∵多边形是正五边形,正五边形的每一个内角为×180°×(5-2)=108°,∴∠O=180°-(180°-108°)×2=36°,∴正五边形的个数是360°÷36°=10.故答案为10.
10.4
解析 连接OD,OC,∵BD=AC,∴,∴∠AOD=
∠BOC,∵∠AOD=∠BOC=,∠DOC=,AB为☉O的直径,
∴2×=180°.解得n=4或n=-2(舍),故答案为4.
11.解析 (1)∵五边形ABCDE是正五边形,
∴∠ABC==108°.
(2)△AMN是正三角形.理由:如图,连接ON,NF,由题意可得FN=OF=ON,∴△FON是等边三角形,∴∠NFA=60°,∴∠NMA=60°,
同理可得∠ANM=60°,∴∠MAN=60°,∴△MAN是正三角形.
(3)∵∠AMN=60°,∴∠AON=120°,
连接OD,则∠AOD=×2=144°,
∴∠NOD=∠AOD-∠AON=144°-120°=24°,
∵360°÷24°=15,∴n的值是15.
素养探究全练
12.解析 (1)如图所示,连接OB,OC,
∵△ABC为正三角形,
∴∠ABC=60°,∠BOC=120°,
∵OC=OB,
∴∠OBC=∠OCB=30°,
∴∠OBM=60°-30°=30°,
∴∠OBM=∠OCN,
又∵BM=CN,OB=OC,∴△OMB≌△ONC,
∴∠BOM=∠CON,∴∠MON=∠BOC=120°.
(2)90°;72°.
(3)∠MON=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
