2024北师大版数学九年级下学期课时练--3.9 弧长及扇形的面积同步练习(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--3.9 弧长及扇形的面积同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 578.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 17:45:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
第三章 圆
9 弧长及扇形的面积
基础过关全练
知识点1 弧长
1.【一题多变·已知圆心角、半径求弧长】(2023辽宁大连中考)圆心角为90°,半径为3的扇形弧长为( )
A.2π B.3π C.π
[变式1·已知弧长、圆心角求半径]一个扇形的弧长是8π cm,圆心角是144°,则此扇形的半径是 cm.
[变式2·已知弧长、半径求圆心角](2023吉林省吉林市一模)图1是等边三角形铁丝框ABC,按如图2所示的方式变形成以A为圆心,AB长为半径的扇形(图形周长保持不变),则所得扇形ABC的圆心角的度数是( )
A.45° B.60° C.
2.(2023福建福州闽侯期中)如图,△ABC内接于☉O,∠BAC=45°,BC=
,则的长是( )
A.π D.π
3.(2021河南中考)如图所示的网格中,每个小正方形的边长均为1,点A,B,D均在小正方形的顶点上,且点B,C在上,∠BAC=22.5°,则的长为 .
4.如图,一个含有30°角的直角三角板ABC在水平桌面上绕点C按顺时针方向旋转到△A'B'C的位置,若BC=15 cm,求顶点A从开始到结束所经过的路径长.
知识点2 扇形面积的计算
5.【中华优秀传统文化】【教材变式·P102T4】(2023湖北巴东期中)扇子最早称“翣”,在我国已有三千多年历史.“打开半个月亮,收起兜里可装.来时荷花初放,去时菊花正黄.”这则谜语说的就是扇子.如图,一竹扇完全打开后,外侧两竹条AB,AC的夹角为135°,AB的长为30 cm,BD的长为20 cm,则扇面面积为( )
A.π cm2 B.600π cm2 C.300π cm2 D.30π cm2
6.【整体思想】如图所示,分别以五边形ABCDE的顶点为圆心,以1为半径作五个圆,则图中阴影部分的面积之和为( )
A.π D.2π
7.【教材变式·P68T1】(2021青海中考)如图,一根5 m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域的面积是( )
A.π m2 B.π m2 C.π m2 D.π m2
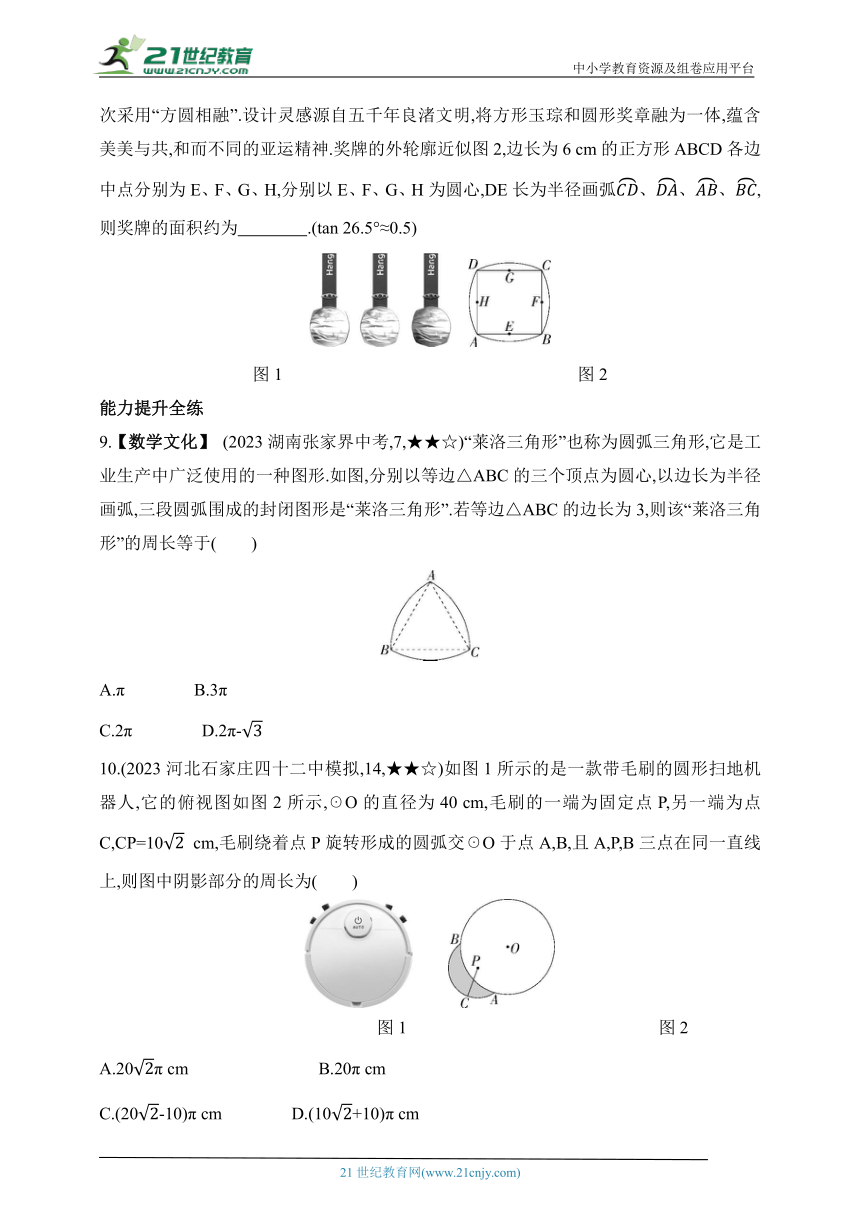
8.【新独家原创】【新素材】如图1,杭州第19届亚运会奖牌取名为“湖山”,它的设计中首次采用“方圆相融”.设计灵感源自五千年良渚文明,将方形玉琮和圆形奖章融为一体,蕴含美美与共,和而不同的亚运精神.奖牌的外轮廓近似图2,边长为6 cm的正方形ABCD各边中点分别为E、F、G、H,分别以E、F、G、H为圆心,DE长为半径画弧,则奖牌的面积约为 .(tan 26.5°≈0.5)
图1 图2
能力提升全练
9.【数学文化】 (2023湖南张家界中考,7,★★☆)“莱洛三角形”也称为圆弧三角形,它是工业生产中广泛使用的一种图形.如图,分别以等边△ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的封闭图形是“莱洛三角形”.若等边△ABC的边长为3,则该“莱洛三角形”的周长等于( )
A.π B.3π
C.2π D.2π-
10.(2023河北石家庄四十二中模拟,14,★★☆)如图1所示的是一款带毛刷的圆形扫地机器人,它的俯视图如图2所示,☉O的直径为40 cm,毛刷的一端为固定点P,另一端为点C,CP=10 cm,毛刷绕着点P旋转形成的圆弧交☉O于点A,B,且A,P,B三点在同一直线上,则图中阴影部分的周长为( )
图1 图2
A.20π cm B.20π cm
C.(20-10)π cm D.(10+10)π cm
11.【将军饮马模型】(2023内蒙古通辽中考,9,★★★)如图,在扇形AOB中,∠AOB=60°,OD平分∠AOB交于点D,点C是半径OB上一动点,若OA=1,则阴影部分周长的最小值为( )
A. C.2
12.(2022广西玉林中考,16,★★☆)数学课上,老师将如图所示的边长为1的正方形铁丝框变形成以A为圆心,AB为半径的扇形(铁丝的粗细忽略不计),则所得扇形DAB的面积是 .
13.(2022江苏泰州中考,23,★★☆)如图①,矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E、F都在直线l上,且AB=7,EF=10,BC>5.点B以1个单位/秒的速度从点E处出发,沿射线EF方向运动,矩形ABCD随之运动,运动时间为t秒.
(1)如图②,当t=2.5时,求半圆O在矩形ABCD内的弧的长度;
(2)【一线三等角模型】在点B运动的过程中,当AD、BC都与半圆O相交时,设这两个交点为G、H,连接OG、OH,若∠GOH为直角,求此时t的值.
素养探究全练
14.【抽象能力】在学习扇形的面积公式时,同学们推得S扇形=,并通过比较扇形面积公式与弧长公式l=,得出扇形面积的另一种计算方法S扇形= lR.接着老师让同学们解决下面两个问题:
问题Ⅰ:求弧长为4π,圆心角为120°的扇形的面积.
问题Ⅱ:某小区设计的花坛形状如图中的阴影部分,已知所在圆的圆心都是点O,的长为l1,的长为l2,AC=BD=d,求该花坛的面积.
(1)请你解答问题Ⅰ.
(2)在解完问题Ⅱ后的全班交流中,有位同学发现扇形面积公式S扇形=lR类似于三角形面积公式,类比梯形面积公式,他猜想花坛的面积S=(l1+l2)d.他的猜想正确吗 如果正确,写出推导过程;如果不正确,请说明理由.
答案全解全析
基础过关全练
1.C 该扇形的弧长为π.故选C.
[变式1] 10
解析 设扇形的半径为r cm,由题意得=8π,解得r=10,
故此扇形的半径是10 cm.
[变式2] D 设AB=BC=x,扇形ABC的圆心角为n°,∴=x,解得n=,∴扇形ABC的圆心角的度数为.
2.C 如图,连接OB、OC,
∵∠BAC=45°,
∴∠BOC=2∠BAC=90°,
∵BC=BC=1,
∴π,故选C.
3.
解析 如图,找到所在圆的圆心O,连接OC.
则半径OB=5,∠BOC=2∠BAC=45°,∴的长=.
4.解析 顶点A从开始到结束所经过的路径是以点C为圆心、AC的长为半径的一段弧,旋转的角度是180°-60°=120°,所以根据弧长公式可得,路径长为=20π(cm).
5.C ∵AB=30 cm,BD=20 cm,∴AD=10 cm,∵∠BAC=135°,∴扇面的面积=S扇形BAC-S扇形DAE==300π(cm2).故选C.
6.C 五边形的内角和为(5-2)×180°=540°,∴题图中圆形的空白部分的面积之和为π,∴题图中阴影部分的面积之和为5π×12-
π.故选C.
方法解读 当所求阴影各个部分扇形的圆心角不确定,但圆心角之和确定时,可以利用整体思想,求出几个扇形的面积之和从而求解.
7.B 如图,小羊A在草地上的最大活动区域是阴影部分,由题意可知,扇形DOE的圆心角是90度,半径是5 m,所以面积=π(m2);扇形ECB的圆心角是180°-120°=60°,半径是5-4=1(m),则面积=(m2),则小羊A在草地上的最大活动区域的面积=π(m2).故选B.
8.cm2
解析 连接DE、GE、CE,则DG=CD=3,EG=6.
在Rt△EDG中,ED=,tan∠DEG==0.5,
∴∠DEG≈26.5°,∴∠DEC=2∠DEG=53°.
S弓形DC=S扇形EDC-S△EDC=CD·EG=π-18,
∴奖牌面积=4S弓形DC+S正方形ABCD=4×cm2.
能力提升全练
9.B ∵△ABC是等边三角形,∴AB=BC=AC=3,∠A=∠B=∠C=60°,
∴的长==π,∴该“莱洛三角形”的周长是3π.故选B.
10.D 连接AB,OA,OB,OP,
∵A,P,B三点在同一直线上,∴AB经过点P,
由题意得AB为半圆的直径,∴PB=PA=CP=10 cm,
∵OA=OB=20 cm,∴OP⊥AB,
在Rt△OAP中,sin∠AOP=,∴∠AOP=45°,
∵OA=OB,OP⊥AB,∴∠BOP=∠AOP=45°,
∴∠AOB=90°,∴l =10π cm,
又l π cm,
∴阴影部分的周长为10+10)π cm,故选D.
11.A 作D点关于直线OB的对称点E,连接OE,AE,AE与OB的交点为C点,此时阴影部分周长最小,最小为AE的长+l .在扇形AOB中,∠AOB=60°,OD平分∠AOB交于点D,∴∠AOD=∠BOD=30°,由轴对称的性质得∠EOB=∠BOD=30°,OE=OD,∴∠AOE=90°,∴△AOE是等腰直角三角形,∵OA=1,∴AE=的长=,∴阴影部分周长的最小值为,故选A.
模型解读 将军饮马模型:如图,直线l同侧有两个定点A、B,请在直线l上找一点C,使AC+BC的值最小.若点A、B在直线l的异侧就好了,这样我们就可以利用“点到点最值模型:两点之间线段最短”找到点C的位置了,即连接AB交直线l于点C.因此,我们可以找点A关于直线l的对称点A',再连接A'B交直线l于点C,点C即为所求.如果将军在河边的另外任一点C'饮马,所走的路程就是AC'+C'B.但是,AC'+C'B
=A'C'+C'B>A'B=A'C+CB=AC+CB.故在点C处饮马,路程最短.
12.1
解析 由题意得的长=CD+BC=1+1=2,
∴S扇形DAB=×2×1=1,故答案为1.
13.解析 (1)如图①,设BC与半圆O交于点M,连接OM,EM,
当t=2.5时,BE=2.5,
∵EF=10,∴OE=EF=5,∴OB=2.5,∴EB=OB,
在矩形ABCD中,∠ABC=90°,∴ME=MO,
又∵MO=EO,∴ME=EO=MO,∴△MOE是等边三角形,
∴∠EOM=60°,∴的长=,
即半圆O在矩形ABCD内的弧的长度为.
图① 图②
(2)如图②,
∵∠GOH=90°,∴∠AOG+∠BOH=90°,
∵∠AGO+∠AOG=90°,∴∠AGO=∠BOH,
在△AGO和△BOH中,
∴△AGO≌△BOH(AAS),∴OB=AG=t-5,
∵AB=7,∴AE=t-7,∴AO=5-(t-7)=12-t,
在Rt△AGO中,AG2+AO2=OG2,
∴(t-5)2+(12-t)2=52,
解得t1=8,t2=9,即t的值为8或9.
素养探究全练
14.解析 (1)设半径为R,由弧长公式,
得=4π,解得R=6,
∴S扇形=×4π×6=12π.
(2)他的猜想正确.理由如下:
设圆心角的度数为n°,
则S扇形AOB=,S扇形COD=,
∴S阴影=(l1+l2)d.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
第三章 圆
9 弧长及扇形的面积
基础过关全练
知识点1 弧长
1.【一题多变·已知圆心角、半径求弧长】(2023辽宁大连中考)圆心角为90°,半径为3的扇形弧长为( )
A.2π B.3π C.π
[变式1·已知弧长、圆心角求半径]一个扇形的弧长是8π cm,圆心角是144°,则此扇形的半径是 cm.
[变式2·已知弧长、半径求圆心角](2023吉林省吉林市一模)图1是等边三角形铁丝框ABC,按如图2所示的方式变形成以A为圆心,AB长为半径的扇形(图形周长保持不变),则所得扇形ABC的圆心角的度数是( )
A.45° B.60° C.
2.(2023福建福州闽侯期中)如图,△ABC内接于☉O,∠BAC=45°,BC=
,则的长是( )
A.π D.π
3.(2021河南中考)如图所示的网格中,每个小正方形的边长均为1,点A,B,D均在小正方形的顶点上,且点B,C在上,∠BAC=22.5°,则的长为 .
4.如图,一个含有30°角的直角三角板ABC在水平桌面上绕点C按顺时针方向旋转到△A'B'C的位置,若BC=15 cm,求顶点A从开始到结束所经过的路径长.
知识点2 扇形面积的计算
5.【中华优秀传统文化】【教材变式·P102T4】(2023湖北巴东期中)扇子最早称“翣”,在我国已有三千多年历史.“打开半个月亮,收起兜里可装.来时荷花初放,去时菊花正黄.”这则谜语说的就是扇子.如图,一竹扇完全打开后,外侧两竹条AB,AC的夹角为135°,AB的长为30 cm,BD的长为20 cm,则扇面面积为( )
A.π cm2 B.600π cm2 C.300π cm2 D.30π cm2
6.【整体思想】如图所示,分别以五边形ABCDE的顶点为圆心,以1为半径作五个圆,则图中阴影部分的面积之和为( )
A.π D.2π
7.【教材变式·P68T1】(2021青海中考)如图,一根5 m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域的面积是( )
A.π m2 B.π m2 C.π m2 D.π m2
8.【新独家原创】【新素材】如图1,杭州第19届亚运会奖牌取名为“湖山”,它的设计中首次采用“方圆相融”.设计灵感源自五千年良渚文明,将方形玉琮和圆形奖章融为一体,蕴含美美与共,和而不同的亚运精神.奖牌的外轮廓近似图2,边长为6 cm的正方形ABCD各边中点分别为E、F、G、H,分别以E、F、G、H为圆心,DE长为半径画弧,则奖牌的面积约为 .(tan 26.5°≈0.5)
图1 图2
能力提升全练
9.【数学文化】 (2023湖南张家界中考,7,★★☆)“莱洛三角形”也称为圆弧三角形,它是工业生产中广泛使用的一种图形.如图,分别以等边△ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的封闭图形是“莱洛三角形”.若等边△ABC的边长为3,则该“莱洛三角形”的周长等于( )
A.π B.3π
C.2π D.2π-
10.(2023河北石家庄四十二中模拟,14,★★☆)如图1所示的是一款带毛刷的圆形扫地机器人,它的俯视图如图2所示,☉O的直径为40 cm,毛刷的一端为固定点P,另一端为点C,CP=10 cm,毛刷绕着点P旋转形成的圆弧交☉O于点A,B,且A,P,B三点在同一直线上,则图中阴影部分的周长为( )
图1 图2
A.20π cm B.20π cm
C.(20-10)π cm D.(10+10)π cm
11.【将军饮马模型】(2023内蒙古通辽中考,9,★★★)如图,在扇形AOB中,∠AOB=60°,OD平分∠AOB交于点D,点C是半径OB上一动点,若OA=1,则阴影部分周长的最小值为( )
A. C.2
12.(2022广西玉林中考,16,★★☆)数学课上,老师将如图所示的边长为1的正方形铁丝框变形成以A为圆心,AB为半径的扇形(铁丝的粗细忽略不计),则所得扇形DAB的面积是 .
13.(2022江苏泰州中考,23,★★☆)如图①,矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E、F都在直线l上,且AB=7,EF=10,BC>5.点B以1个单位/秒的速度从点E处出发,沿射线EF方向运动,矩形ABCD随之运动,运动时间为t秒.
(1)如图②,当t=2.5时,求半圆O在矩形ABCD内的弧的长度;
(2)【一线三等角模型】在点B运动的过程中,当AD、BC都与半圆O相交时,设这两个交点为G、H,连接OG、OH,若∠GOH为直角,求此时t的值.
素养探究全练
14.【抽象能力】在学习扇形的面积公式时,同学们推得S扇形=,并通过比较扇形面积公式与弧长公式l=,得出扇形面积的另一种计算方法S扇形= lR.接着老师让同学们解决下面两个问题:
问题Ⅰ:求弧长为4π,圆心角为120°的扇形的面积.
问题Ⅱ:某小区设计的花坛形状如图中的阴影部分,已知所在圆的圆心都是点O,的长为l1,的长为l2,AC=BD=d,求该花坛的面积.
(1)请你解答问题Ⅰ.
(2)在解完问题Ⅱ后的全班交流中,有位同学发现扇形面积公式S扇形=lR类似于三角形面积公式,类比梯形面积公式,他猜想花坛的面积S=(l1+l2)d.他的猜想正确吗 如果正确,写出推导过程;如果不正确,请说明理由.
答案全解全析
基础过关全练
1.C 该扇形的弧长为π.故选C.
[变式1] 10
解析 设扇形的半径为r cm,由题意得=8π,解得r=10,
故此扇形的半径是10 cm.
[变式2] D 设AB=BC=x,扇形ABC的圆心角为n°,∴=x,解得n=,∴扇形ABC的圆心角的度数为.
2.C 如图,连接OB、OC,
∵∠BAC=45°,
∴∠BOC=2∠BAC=90°,
∵BC=BC=1,
∴π,故选C.
3.
解析 如图,找到所在圆的圆心O,连接OC.
则半径OB=5,∠BOC=2∠BAC=45°,∴的长=.
4.解析 顶点A从开始到结束所经过的路径是以点C为圆心、AC的长为半径的一段弧,旋转的角度是180°-60°=120°,所以根据弧长公式可得,路径长为=20π(cm).
5.C ∵AB=30 cm,BD=20 cm,∴AD=10 cm,∵∠BAC=135°,∴扇面的面积=S扇形BAC-S扇形DAE==300π(cm2).故选C.
6.C 五边形的内角和为(5-2)×180°=540°,∴题图中圆形的空白部分的面积之和为π,∴题图中阴影部分的面积之和为5π×12-
π.故选C.
方法解读 当所求阴影各个部分扇形的圆心角不确定,但圆心角之和确定时,可以利用整体思想,求出几个扇形的面积之和从而求解.
7.B 如图,小羊A在草地上的最大活动区域是阴影部分,由题意可知,扇形DOE的圆心角是90度,半径是5 m,所以面积=π(m2);扇形ECB的圆心角是180°-120°=60°,半径是5-4=1(m),则面积=(m2),则小羊A在草地上的最大活动区域的面积=π(m2).故选B.
8.cm2
解析 连接DE、GE、CE,则DG=CD=3,EG=6.
在Rt△EDG中,ED=,tan∠DEG==0.5,
∴∠DEG≈26.5°,∴∠DEC=2∠DEG=53°.
S弓形DC=S扇形EDC-S△EDC=CD·EG=π-18,
∴奖牌面积=4S弓形DC+S正方形ABCD=4×cm2.
能力提升全练
9.B ∵△ABC是等边三角形,∴AB=BC=AC=3,∠A=∠B=∠C=60°,
∴的长==π,∴该“莱洛三角形”的周长是3π.故选B.
10.D 连接AB,OA,OB,OP,
∵A,P,B三点在同一直线上,∴AB经过点P,
由题意得AB为半圆的直径,∴PB=PA=CP=10 cm,
∵OA=OB=20 cm,∴OP⊥AB,
在Rt△OAP中,sin∠AOP=,∴∠AOP=45°,
∵OA=OB,OP⊥AB,∴∠BOP=∠AOP=45°,
∴∠AOB=90°,∴l =10π cm,
又l π cm,
∴阴影部分的周长为10+10)π cm,故选D.
11.A 作D点关于直线OB的对称点E,连接OE,AE,AE与OB的交点为C点,此时阴影部分周长最小,最小为AE的长+l .在扇形AOB中,∠AOB=60°,OD平分∠AOB交于点D,∴∠AOD=∠BOD=30°,由轴对称的性质得∠EOB=∠BOD=30°,OE=OD,∴∠AOE=90°,∴△AOE是等腰直角三角形,∵OA=1,∴AE=的长=,∴阴影部分周长的最小值为,故选A.
模型解读 将军饮马模型:如图,直线l同侧有两个定点A、B,请在直线l上找一点C,使AC+BC的值最小.若点A、B在直线l的异侧就好了,这样我们就可以利用“点到点最值模型:两点之间线段最短”找到点C的位置了,即连接AB交直线l于点C.因此,我们可以找点A关于直线l的对称点A',再连接A'B交直线l于点C,点C即为所求.如果将军在河边的另外任一点C'饮马,所走的路程就是AC'+C'B.但是,AC'+C'B
=A'C'+C'B>A'B=A'C+CB=AC+CB.故在点C处饮马,路程最短.
12.1
解析 由题意得的长=CD+BC=1+1=2,
∴S扇形DAB=×2×1=1,故答案为1.
13.解析 (1)如图①,设BC与半圆O交于点M,连接OM,EM,
当t=2.5时,BE=2.5,
∵EF=10,∴OE=EF=5,∴OB=2.5,∴EB=OB,
在矩形ABCD中,∠ABC=90°,∴ME=MO,
又∵MO=EO,∴ME=EO=MO,∴△MOE是等边三角形,
∴∠EOM=60°,∴的长=,
即半圆O在矩形ABCD内的弧的长度为.
图① 图②
(2)如图②,
∵∠GOH=90°,∴∠AOG+∠BOH=90°,
∵∠AGO+∠AOG=90°,∴∠AGO=∠BOH,
在△AGO和△BOH中,
∴△AGO≌△BOH(AAS),∴OB=AG=t-5,
∵AB=7,∴AE=t-7,∴AO=5-(t-7)=12-t,
在Rt△AGO中,AG2+AO2=OG2,
∴(t-5)2+(12-t)2=52,
解得t1=8,t2=9,即t的值为8或9.
素养探究全练
14.解析 (1)设半径为R,由弧长公式,
得=4π,解得R=6,
∴S扇形=×4π×6=12π.
(2)他的猜想正确.理由如下:
设圆心角的度数为n°,
则S扇形AOB=,S扇形COD=,
∴S阴影=(l1+l2)d.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
