人教版五年级数学上册第六单元多边形的面积同步学案(知识点梳理+能力百分练)三
文档属性
| 名称 | 人教版五年级数学上册第六单元多边形的面积同步学案(知识点梳理+能力百分练)三 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 06:20:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版五年级数学上册第六单元多边形的面积(知识点梳理+能力百分练)三
知识点梳理
1、通过拆分平移,平行四边形的面积可以转换为以它的底和高为长宽的长方形的面积。所以平行四边形的面积=底×高,或S=ah。由此可得等底等高的平行四边形面积相等。
2、任意两个相同的三角形可以拼成一个与它等底等高的平行四边形,所以三角形的面积可以看成与它等底等高的平行四边形的面积的一半。即三角形的面积=底×高÷2或S=ah÷2。
3、任意两个相同的梯形可以拼成一个与它等底等高的平行四边形,这个平行四边形的底是梯形上下底之和,高是梯形的高,所以梯形的面积可以看成以梯形上底与下底的和为底,以梯形的高为高的平行四边形的一半。即梯形的面积=(上底+下底)×高÷2或S=(a+b)h÷2。
4、求组合图形的面积可以用割补拼接使其成为基本图形来计算,或者用基本图形面积做和差计算。
能力百分练
一、选择题(共16分)
1.一个三角形与一个平行四边形的底和面积都相等,已知平行四边形的高是7厘米,三角形的高是( )厘米。
A.5 B.7 C.14 D.21
2.计算下图的面积(单位:厘米)。
聪聪的算法是:(7+12)×8÷2+10×(12-7)÷2。下面能表示聪聪的思考过程的图示是( )。
A. B.
C. D.
3.把一个长方形框架拉成平行四边形,面积变小了是因为( )。
A.底变短了 B.高变短了
C.周长变短了 D.底和高都变短了
4.下面哪道题可以用方程4=24来解答( )。
A.一个三角形的面积是24平方米,底是4米,高是多少米?
B.把24支铅笔平均分给4个小朋友,每个小朋友分得多少支?
C.小明有24本课外书,比小芳多4本,小芳有多少本课外书?
D.小明看一本故事书,平均每天看24页,4天可以看多少页?
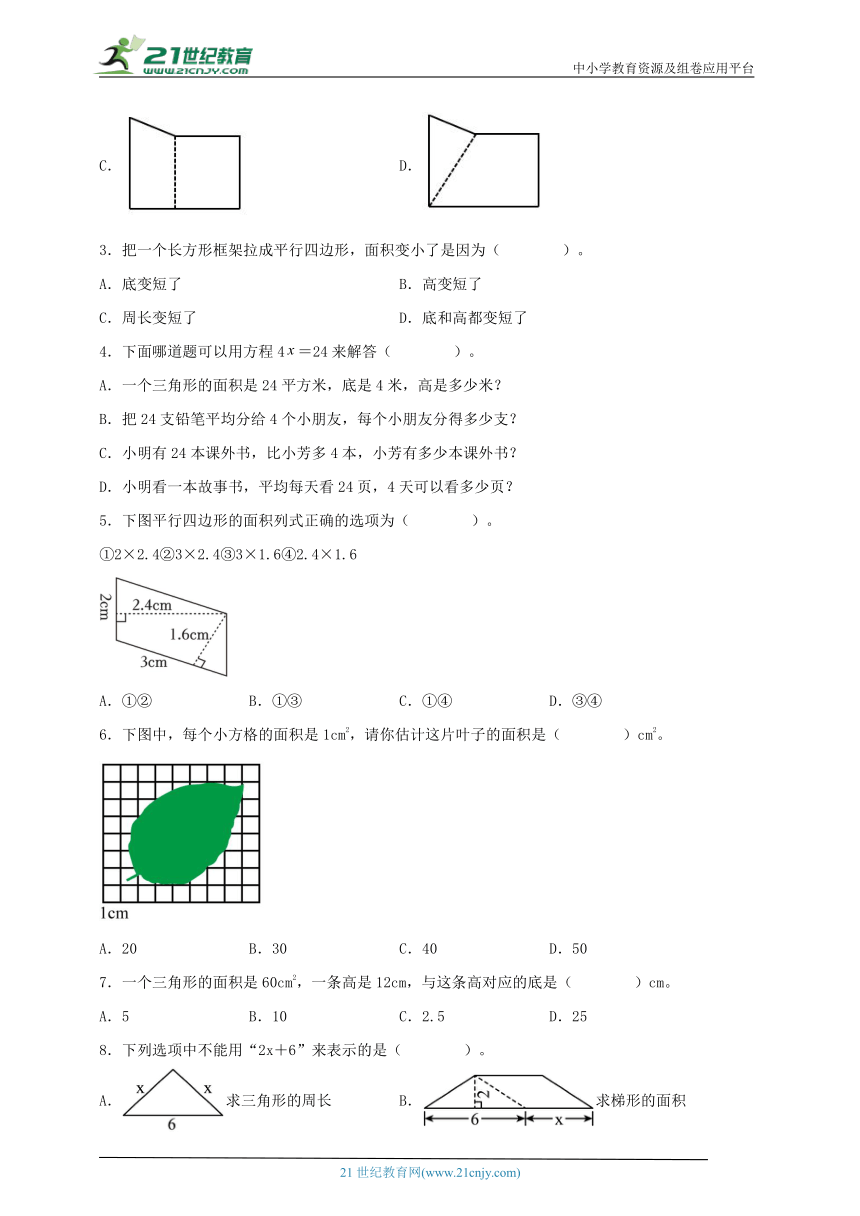
5.下图平行四边形的面积列式正确的选项为( )。
①2×2.4②3×2.4③3×1.6④2.4×1.6
A.①② B.①③ C.①④ D.③④
6.下图中,每个小方格的面积是1cm2,请你估计这片叶子的面积是( )cm2。
A.20 B.30 C.40 D.50
7.一个三角形的面积是60cm2,一条高是12cm,与这条高对应的底是( )cm。
A.5 B.10 C.2.5 D.25
8.下列选项中不能用“2x+6”来表示的是( )。
A.求三角形的周长 B.求梯形的面积
C.求线段的总长度 D.小明有x元,小红的钱数比小明多6元,求两人的总钱数。
二、填空题(共16分)
9.下边梯形的高是( )厘米,面积是( )平方厘米。
10.一个三角形的面积是15.6平方厘米,底是3厘米,高是( )厘米。
11.一个面积是20平方厘米的三角形,如果把它的底扩大到原来的2倍,高缩小到原来的一半,那么变化后三角形的面积是( )平方厘米;如果把它的底缩小到原来的一半,高扩大到原来的1.2倍,那么变化后三角形的面积是( )平方厘米。
12.一个梯形的面积是,已知上、下底的和是25m,则它的高是( )m。
13.有一块平行四边形菜地(如图所示),如果在它的四边围上篱笆,篱笆长( )米。
14.一个平形四边形的底是8分米,高是0.9分米,它的面积是( )平方分米,和它等底等高的三角形的面积是( )平方分米。
15.靠墙边围成一个梯形花坛(如下图),围花坛的篱笆长52m,这个花坛的面积是( )。
16.下图中每个小方格的面积是1cm2,请你估计这片叶子的面积约是( )cm2。
三、判断题(共8分)
17.如果一个梯形的面积是50cm2,上底和下底的和是10cm,那么这个梯形的高是5cm。( )
18.我们在进行梯形面积公式的推导时,也可以把梯形转化成两个三角形进行推导。( )
19.把一个平行四边形拉成一个长方形,它的面积和周长都不变。( )
20.把一个平行四边形框架拉成了一个长方形。已知这个长方形的长是8cm、宽是5cm,面积是40cm2,所以原来的平行四边形的面积也是40cm2。( )
四、计算题(共12分)
21.(6分)计算阴影部分的面积。
22.(6分)求组合图形的面积。(单位:米)
五、作图题(共6分)
23.(6分)在下面的方格纸上画出一个平行四边形、一个三角形和一个梯形,使所画图形的面积都是12平方厘米且高相等。(每个小方格都是1平方厘米)
六、解答题(共42分)
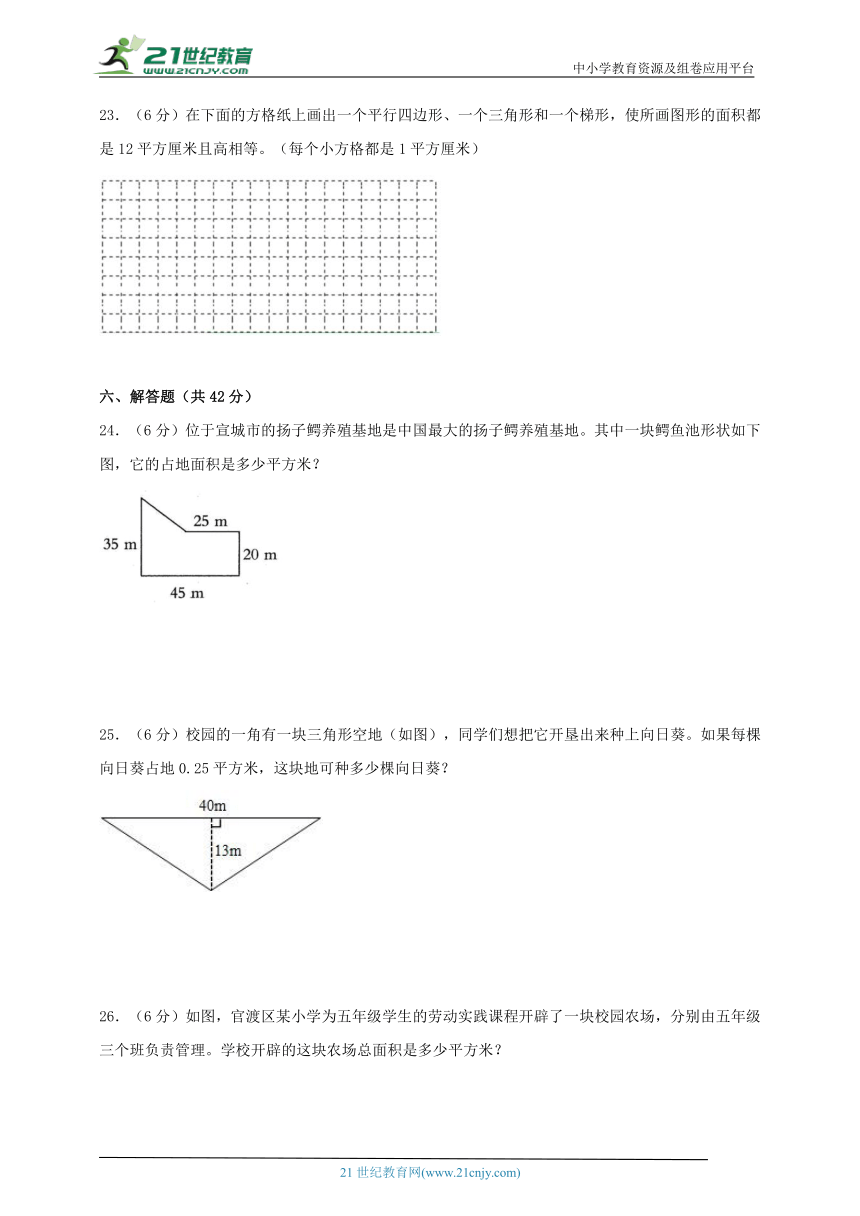
24.(6分)位于宣城市的扬子鳄养殖基地是中国最大的扬子鳄养殖基地。其中一块鳄鱼池形状如下图,它的占地面积是多少平方米?
25.(6分)校园的一角有一块三角形空地(如图),同学们想把它开垦出来种上向日葵。如果每棵向日葵占地0.25平方米,这块地可种多少棵向日葵?
26.(6分)如图,官渡区某小学为五年级学生的劳动实践课程开辟了一块校园农场,分别由五年级三个班负责管理。学校开辟的这块农场总面积是多少平方米?
27.(6分)果园里有一块平行四边形的地,一共栽了9600棵果树,平均每棵果树占地0.5平方米,这块地有多少平方米?平行四边形地的底是100米,底边上的高是多少?
28.(6分)学校要粉刷一面墙(如下图),每平方米需要0.15千克涂料,至少需要准备多少千克涂料?
29.(6分)一块平行四边形的广告牌,底是12.5米,高6.4米,现在要给这块广告牌的正反两面刷防水漆,每平方米用油漆0.8千克,共需要多少千克防水漆?
30.(6分)汽车的前挡风玻璃大都是梯形,这样的设计不仅美观,而且可以大大提高司机的视野。如果这种玻璃的造价是每平方米600元,算一算,这块玻璃的价格大概是多少元?
参考答案
1.C
【分析】根据三角形的面积=底×高÷2,平行四边形的面积=底×高,如果一个三角形与一个平行四边形的底和面积都相等时,则三角形的高等于平行四边形的高的2倍,用平行四边形的高乘2即可求出三角形的高。
【详解】7×2=14(厘米)
即三角形的高是14厘米。
故答案为:C
【点睛】此题的解题关键是灵活运用三角形和平行四边形的面积公式以及它们之间的关系求解。
2.D
【分析】根据求组合图形的面积的方法,用“割补法”把组合图形割成几个不同的图形或补成其它的图形,据此逐一分析各项即可。
【详解】A.把这个组合图形补成一个长方形,此时该图形的面积等于长方形的面积减去梯形的面积,列式为:10×12-(7+12)×(10-8)÷2,不符合题意;
B.把该图形割成一个三角形和一个长方形,此时该图形的面积等于三角形的面积加上长方形的面积,列式为:12×8+(12-7)×(10-8)÷2,不符合题意;
C.把该图形割成一个梯形和一个长方形,此时该图形的面积等于梯形的面积加上长方形的面积,列式为:7×8+(8+10)×(12-7)÷2,不符合题意;
D.把该图形割成一个三角形和一个梯形,此时该图形的面积等于三角形的面积加上梯形的面积,列式为:(7+12)×8÷2+10×(12-7)÷2,符合题意;
故答案为:D
【点睛】本题考查组合图形的面积,明确运用“割补法”是解题的关键。
3.B
【分析】把一个长方形框架拉成平行四边形,长方形的长=平行四边形的底,长方形的宽>平行四边形的高,据此分析。
【详解】根据分析,把一个长方形框架拉成平行四边形,长方形面积=长×宽>平行四边形的底×高=平行四边形面积,面积变小了是因为高变短了。
故答案为:B
【点睛】关键是熟悉长方形和平行四边形的特征,掌握并灵活运用平行四边形面积公式。
4.B
【分析】A.根据三角形的面积=底×高÷2,据此列出方程;
B.根据题意可得等量关系:每个小朋友分得的支数×小朋友的人数=铅笔的总支数,据此列出方程;
C.根据题意可得等量关系:小芳课外书的本数+4=小明课外书的本数,据此列出方程;
D.根据题意可得等量关系:4天看的总页数÷4=平均每天看的页数,据此列出方程。
【详解】A.设高为米,列方程为:4÷2=24,不符合题意;
B.设每个小朋友分得支,列方程为:4=24,符合题意;
C.设小芳有本课外书,列方程为:+4=24,不符合题意;
D.设小明4天可以看页,列方程为:÷4=24,不符合题意。
故答案为:B
【点睛】本题考查列方程解决问题,从题目中找到等量关系,按等量关系列出方程。
5.B
【分析】平行四边形面积=底×高,注意公式中的底和高指的是对应的一组底和高,据此分析。
【详解】2×2.4=4.8(平方厘米)
3×1.6=4.8(平方厘米)
所以列式正确的选项为①③。
故答案为:B
【点睛】关键是掌握并灵活运用平行四边形面积公式。
6.B
【分析】估计不规则图形的面积时,可以根据图形的特点转化成已学过的图形,再利用面积公式来估算面积。
【详解】将叶子的形状近似地看成平行四边形,如下图,底是5cm,高是6cm。
根据平行四边形的面积=底×高计算,5×6=30(cm2),所以这片叶子的面积约是30cm2。
故答案为:B
【点睛】估计不规则图形的面积也可以用数方格的方法,不满一格的都按半格计算。
7.B
【分析】三角形的面积=底×高÷2,则底=面积×2÷高,据此解答即可。
【详解】60×2÷12
=120÷12
=10(cm)
与这条高对应的底是10cm。
故答案为:B
【点睛】此题主要考查三角形面积的计算方法的灵活应用。
8.C
【分析】根据三角形周长=三条线段的长度和;梯形面积=(上底十下底)×高÷2,分别表示出三角形的周长,梯形的面积,总钱数以及线段的长度,再选择即可。
【详解】A.三角形的周长x+x+6=2x+6;
B.梯形的面积(x+6+x)×2÷2
=(2x+6)×2÷2
=2x+6;
C.线段的总长度2+x+6=x+8;
D.两人的总钱数x+6+x=2x+6。
故答案为:C
【点睛】此题考查了用字母表示数的方法,关键是弄清题中字母所表示的意义,再进一步解答。
9. 12 162
【分析】一腰垂直于底的梯形叫直角梯形。梯形的上底为9厘米,下底为18厘米,则梯形的高为12厘米;根据梯形的面积=(上底+下底)×高÷2,代入数据即可求出梯形的面积。
【详解】梯形的高是12厘米。
(9+18)×12÷2
=27×12÷2
=162(平方厘米)
即梯形的面积是162平方厘米。
【点睛】此题的解题关键是理解掌握梯形的特征以及梯形的面积的计算方法。
10.10.4
【分析】由“三角形的面积=底×高÷2”可得“三角形的高=三角形的面积×2÷底”,三角形的面积和底已知,代入关系式即可求解。
【详解】15.6×2÷3
=31.2÷3
=10.4(厘米)
所以,这个三角形的高是10.4厘米。
【点睛】此题主要考查三角形的面积的计算方法的灵活应用。
11. 20 12
【分析】三角形的面积=底×高÷2;一个因数不变,另一个因数扩大到原来的几倍或缩小到原来的几分之一(0除外),积也扩大到原来几倍或缩小到原来的几分之一;如果一个因数扩大到原来几倍或缩小到原来的几分之一,另一个因数反而缩小到原来的几分之一或扩大到相同的倍数(0除外),那么积不变。据此解答。
【详解】20×2÷2=20(平方厘米)
20÷2×1.2=12(平方厘米)
一个面积是20平方厘米的三角形,如果把它的底扩大到原来的2倍,高缩小到原来的一半,那么变化后三角形的面积是20平方厘米;如果把它的底缩小到原来的一半,高扩大到原来的1.2倍,那么变化后三角形的面积是12平方厘米。
【点睛】本题考查了三角形面积公式的灵活应用以及积的变化规律。
12.16
【分析】根据梯形的高=面积×2÷上下底的和,列式计算即可。
【详解】200×2÷25=16(m)
它的高是16m。
【点睛】关键是掌握并灵活运用梯形面积公式。
13.192
【分析】根据“平行四边形面积=底×高”可知,平行四边形的底=平行四边形的面积÷高,据此先求出平行四边形的面积,再求出平行四边形另一条边的长度;然后求出平行四边形的周长即可。
【详解】60×30÷50
=1800÷50
=36(米)
(60+36)×2
=96×2
=192(平方米)
所以,篱笆长192米。
【点睛】熟记平行四边形面积、周长计算公式,是解答此题是关键。
14. 7.2 3.6
【分析】先根据平行四边形的面积公式求出平行四边形的面积;再根据三角形的面积是与它等底等高的平行四边形面积的一半,即可求出三角形的面积。
【详解】8×0.9=7.2(平方分米)
平行四边形的面积是7.2平方分米,
7.2÷2=3.6(平方分米)
和它等底等高的三角形的面积是3.6平方分米。
【点睛】解答此题的关键是掌握平行四边形的面积公式以及三角形的面积是和它等底等高的平行四边形面积的一半。
15.320
【分析】因为围花坛的篱笆长52m,由图可知:梯形花坛的高为20m,用“52-20”求出上底和下底的和,进而根据“梯形的面积=(上底+下底)×高÷2”解答即可。
【详解】(52-20)×20÷2
=32×20÷2
=640÷2
=320(m2)
这个花坛的面积是320m2。
【点睛】此题考查的是梯形面积计算公式的运用,理解“52-20”是上底和下底的和是本题的关键。
16.22
【分析】不规则图形的面积估算方法:数格子,分别数出满格和不满格的数量,不满格的数量按半格计算,再加上满格的数量,就是不规则图形的格子数,最后乘每个小方格的面积即可。
【详解】满格有14个,不满格有16个;
一共有:
14+16÷2
=14+8
=22(个)
面积:1×22=22(cm2)
估计这片叶子的面积约是22cm2。
(答案不唯一)
【点睛】掌握不规则图形面积的估算方法是解题的关键。
17.×
【分析】由梯形的面积公式可推导出:梯形的高=梯形的面积×2÷(上底+下底),把梯形的面积、上底和下底的和代入计算出高即可。
【详解】50×2÷10
=100÷10
=10(cm)
10≠5
所以这个梯形的高是10cm。原题说法错误。
故答案为:×
【点睛】计算梯形的面积时,不要忘记除以2。
18.√
【分析】如图所示,连接梯形ABCD的对角线AC,把梯形分成两个等高的三角形,利用“三角形的面积=底×高÷2”表示出三角形ABC和三角形ACD的面积,梯形的面积=三角形ABC的面积+三角形ACD的面积,据此解答。
【详解】
上底×高÷2+下底×高÷2
=上底×(高÷2)+下底×(高÷2)
=(上底+下底)×(高÷2)
=(上底+下底)×高÷2
所以,梯形的面积=(上底+下底)×高÷2。
由上可知,我们在进行梯形面积公式的推导时,也可以把梯形转化成两个三角形进行推导。
故答案为:√
【点睛】熟记三角形的面积计算公式,并掌握梯形面积公式的推导过程是解答题目的关键。
19.×
【分析】把一个平行四边形拉成一个长方形,四边的长度不变,则周长不变,根据平行四边形的面积公式:S=ah,长方形的面积公式:S=ab,把一个平行四边形拉成一个长方形(边长不变),由于长方形的宽大于平行四边形的高,所以拉成长方形的面积大于平行四边形的面积。据此解答。
【详解】因为把平行四边形拉成长方形,四个边的长度没变,则其周长不变;
但是它的高变长了,所以它的面积就变大了。
所以原题说法错误。
故答案为:×
【点睛】本题考查了平行四边形、长方形的特征和性质,理解掌握平行四边形的面积公式、长方形的面积公式的灵活运用,关键是熟记公式。
20.×
【分析】把一个平行四边形框架拉成了一个长方形之后,长方形的宽大于平行四边形的高,长方形的长等于平行四边形的底。所以长方形的面积比原来平行四边形的面积大。
【详解】把一个平行四边形框架拉成了一个长方形之后,长方形的宽大于平行四边形的高,大于5cm,长方形的长等于平行四边形的底是8cm ,所以长方形的面积比原来平行四边形的面积大,原来平行四边形的面积小于40cm2。
故答案为:×
【点睛】解答此题的关键是:把一个平行四边形拉成长方形之后,长方形的宽大于平行四边形的高,长方形的长等于平行四边形的底,最后算出的面积比平行四边形的面积大。
21.80平方厘米
【分析】阴影部分是由一个底为12厘米,高为5厘米的三角形和一个上底为12厘米,下底为8厘米,高为5厘米的梯形组合而成,那么分别利用三角形和梯形的面积公式求出这两个图形的面积,再相加即可求出阴影部分的面积。
【详解】12×5÷2+(12+8)×5÷2
=60÷2+20×5÷2
=30+50
=80(平方厘米)
即阴影部分的面积是80平方厘米。
22.63.7平方米
【分析】观察图形可知,组合图形的面积=三角形的面积+平行四边形的面积,根据三角形的面积=底×高÷2,平行四边形的面积=底×高,代入数据计算求解。
【详解】三角形的面积:
9.8×3÷2
=29.4÷2
=14.7(平方米)
平行四边形的面积:
9.8×5=49(平方米)
一共:14.7+49=63.7(平方米)
组合图形的面积是63.7平方米。
23.见详解
【分析】已知平行四边形、三角形、梯形的面积都是12平方厘米,且高相等;根据平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,由此确定平行四边形的底和高、三角形的底和高、梯形的上底、下底和高,据此画出符合要求的图形。
【详解】平行四边形的面积:3×4=12(平方厘米)
三角形的面积:6×4÷2=12(平方厘米)
梯形的面积:
(2+4)×4÷2
=6×4÷2
=12(平方厘米)
画一个底为3厘米、高为4厘米的平行四边形;
画一个底为6厘米、高为4厘米的三角形;
画一个上底为2厘米、下底为4厘米、高为4厘米的梯形。
如图:
(答案不唯一)
【点睛】本题考查画指定面积的平行四边形、三角形和梯形,掌握平行四边形、三角形、梯形的面积公式是解题的关键。
24.1050平方米
【分析】如图:这块鳄鱼池是由一个长为45米,宽为20米的长方形和一个底为(45-25)米,高为(35-20)米的三角形组合而成,分别利用长方形和三角形的面积公式求出这两个图形的面积,再相加即可得解。
【详解】45×20+(45-25)×(35-20)÷2
=900+20×15÷2
=900+150
=1050(平方米)
答:它的占地面积是1050平方米。
【点睛】此题主要考查组合图形的面积的计算方法,灵活运用长方形和三角形的面积公式求解。
25.1040棵
【分析】根据三角形的面积=底×高÷2,已知这块三角形空地的底边长是40米,高是13米,代入到公式中即可求出这块三角形空地的面积,再除以每棵向日葵占地0.25平方米,即可求出这块地可种多少棵向日葵。
【详解】40×13÷2÷0.25
=520÷2÷0.25
=1040(棵)
答:这块地可种1040棵向日葵。
【点睛】此题的解题关键是灵活运用三角形的面积公式解决实际问题。
26.312.5平方米
【分析】观察图意可知,学校开辟的这块农场总面积=底和高都是15米的三角形面积+底和高都是20米的三角形面积,据此根据“三角形面积=底×高÷2”,即可解题。
【详解】15×15÷2+20×20÷2
=225÷2+400÷2
=112.5+200
=312.5(平方米)
答:学校开辟的这块农场总面积是312.5平方米。
【点睛】熟记三角形面积计算公式,是解答此题的关键。
27.4800平方米;48米
【分析】平均每棵果树占地0.5平方米,那么9600棵树就有9600个0.5,用9600×0.5即可求出这块地的面积;平行四边形的面积=底×高,所以高=面积÷底,代入数据计算即可求解。
【详解】9600×0.5=4800(平方米)
4800÷100=48(米)
答:这块地的面积有4800平方米,底边的高是48米。
【点睛】此题考查小数乘法的计算以及平行四边形面积公式的灵活应用。
28.6千克
【分析】由图意可知:这面墙由1个梯形和1个长方形组成;利用梯形的面积=(上底+下底)×高÷2和长方形的面积=长×宽,求出梯形和长方形的面积,再相加即可求解。
【详解】(4+8)×2÷2+8×3.5
=12×2÷2+28
=24÷2+28
=12+28
=40(平方米)
0.15×40=6(千克).
答:至少需要准备6千克涂料。
【点睛】本题考查的是组合图形的面积,解答此题的关键是:弄清楚这面墙有哪几个图形组成,进而求其面积,问题即可逐步得解。
29.128千克
【分析】根据平行四边形的面积公式:S=ah,据此求出广告牌的面积,再乘2即可求出这块广告牌的正反两面的面积,最后再乘0.8即可。
【详解】12.5×6.4×2×0.8
=80×2×0.8
=160×0.8
=128(千克)
答:共需要128千克防水漆。
【点睛】本题考查平行四边形的面积,熟记公式是解题的关键。
30.514.5元
【分析】先根据梯形的面积=(上底+下底)×高÷2,把数据代入公式求出挡风玻璃的面积,再根据每平方米600元,用单价×面积求出这块玻璃的总价格即可。
【详解】(100+145)×70÷2
=245×70÷2
=17150÷2
=8575(平方厘米)
8575平方厘米=0.8575平方米
600×0.8575=514.5(元)
答:这块玻璃的价格大概是514.5元。
【点睛】掌握梯形面积公式以及经济问题的基本数量关系是解题的关键,计算时要注意单位换算一致。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版五年级数学上册第六单元多边形的面积(知识点梳理+能力百分练)三
知识点梳理
1、通过拆分平移,平行四边形的面积可以转换为以它的底和高为长宽的长方形的面积。所以平行四边形的面积=底×高,或S=ah。由此可得等底等高的平行四边形面积相等。
2、任意两个相同的三角形可以拼成一个与它等底等高的平行四边形,所以三角形的面积可以看成与它等底等高的平行四边形的面积的一半。即三角形的面积=底×高÷2或S=ah÷2。
3、任意两个相同的梯形可以拼成一个与它等底等高的平行四边形,这个平行四边形的底是梯形上下底之和,高是梯形的高,所以梯形的面积可以看成以梯形上底与下底的和为底,以梯形的高为高的平行四边形的一半。即梯形的面积=(上底+下底)×高÷2或S=(a+b)h÷2。
4、求组合图形的面积可以用割补拼接使其成为基本图形来计算,或者用基本图形面积做和差计算。
能力百分练
一、选择题(共16分)
1.一个三角形与一个平行四边形的底和面积都相等,已知平行四边形的高是7厘米,三角形的高是( )厘米。
A.5 B.7 C.14 D.21
2.计算下图的面积(单位:厘米)。
聪聪的算法是:(7+12)×8÷2+10×(12-7)÷2。下面能表示聪聪的思考过程的图示是( )。
A. B.
C. D.
3.把一个长方形框架拉成平行四边形,面积变小了是因为( )。
A.底变短了 B.高变短了
C.周长变短了 D.底和高都变短了
4.下面哪道题可以用方程4=24来解答( )。
A.一个三角形的面积是24平方米,底是4米,高是多少米?
B.把24支铅笔平均分给4个小朋友,每个小朋友分得多少支?
C.小明有24本课外书,比小芳多4本,小芳有多少本课外书?
D.小明看一本故事书,平均每天看24页,4天可以看多少页?
5.下图平行四边形的面积列式正确的选项为( )。
①2×2.4②3×2.4③3×1.6④2.4×1.6
A.①② B.①③ C.①④ D.③④
6.下图中,每个小方格的面积是1cm2,请你估计这片叶子的面积是( )cm2。
A.20 B.30 C.40 D.50
7.一个三角形的面积是60cm2,一条高是12cm,与这条高对应的底是( )cm。
A.5 B.10 C.2.5 D.25
8.下列选项中不能用“2x+6”来表示的是( )。
A.求三角形的周长 B.求梯形的面积
C.求线段的总长度 D.小明有x元,小红的钱数比小明多6元,求两人的总钱数。
二、填空题(共16分)
9.下边梯形的高是( )厘米,面积是( )平方厘米。
10.一个三角形的面积是15.6平方厘米,底是3厘米,高是( )厘米。
11.一个面积是20平方厘米的三角形,如果把它的底扩大到原来的2倍,高缩小到原来的一半,那么变化后三角形的面积是( )平方厘米;如果把它的底缩小到原来的一半,高扩大到原来的1.2倍,那么变化后三角形的面积是( )平方厘米。
12.一个梯形的面积是,已知上、下底的和是25m,则它的高是( )m。
13.有一块平行四边形菜地(如图所示),如果在它的四边围上篱笆,篱笆长( )米。
14.一个平形四边形的底是8分米,高是0.9分米,它的面积是( )平方分米,和它等底等高的三角形的面积是( )平方分米。
15.靠墙边围成一个梯形花坛(如下图),围花坛的篱笆长52m,这个花坛的面积是( )。
16.下图中每个小方格的面积是1cm2,请你估计这片叶子的面积约是( )cm2。
三、判断题(共8分)
17.如果一个梯形的面积是50cm2,上底和下底的和是10cm,那么这个梯形的高是5cm。( )
18.我们在进行梯形面积公式的推导时,也可以把梯形转化成两个三角形进行推导。( )
19.把一个平行四边形拉成一个长方形,它的面积和周长都不变。( )
20.把一个平行四边形框架拉成了一个长方形。已知这个长方形的长是8cm、宽是5cm,面积是40cm2,所以原来的平行四边形的面积也是40cm2。( )
四、计算题(共12分)
21.(6分)计算阴影部分的面积。
22.(6分)求组合图形的面积。(单位:米)
五、作图题(共6分)
23.(6分)在下面的方格纸上画出一个平行四边形、一个三角形和一个梯形,使所画图形的面积都是12平方厘米且高相等。(每个小方格都是1平方厘米)
六、解答题(共42分)
24.(6分)位于宣城市的扬子鳄养殖基地是中国最大的扬子鳄养殖基地。其中一块鳄鱼池形状如下图,它的占地面积是多少平方米?
25.(6分)校园的一角有一块三角形空地(如图),同学们想把它开垦出来种上向日葵。如果每棵向日葵占地0.25平方米,这块地可种多少棵向日葵?
26.(6分)如图,官渡区某小学为五年级学生的劳动实践课程开辟了一块校园农场,分别由五年级三个班负责管理。学校开辟的这块农场总面积是多少平方米?
27.(6分)果园里有一块平行四边形的地,一共栽了9600棵果树,平均每棵果树占地0.5平方米,这块地有多少平方米?平行四边形地的底是100米,底边上的高是多少?
28.(6分)学校要粉刷一面墙(如下图),每平方米需要0.15千克涂料,至少需要准备多少千克涂料?
29.(6分)一块平行四边形的广告牌,底是12.5米,高6.4米,现在要给这块广告牌的正反两面刷防水漆,每平方米用油漆0.8千克,共需要多少千克防水漆?
30.(6分)汽车的前挡风玻璃大都是梯形,这样的设计不仅美观,而且可以大大提高司机的视野。如果这种玻璃的造价是每平方米600元,算一算,这块玻璃的价格大概是多少元?
参考答案
1.C
【分析】根据三角形的面积=底×高÷2,平行四边形的面积=底×高,如果一个三角形与一个平行四边形的底和面积都相等时,则三角形的高等于平行四边形的高的2倍,用平行四边形的高乘2即可求出三角形的高。
【详解】7×2=14(厘米)
即三角形的高是14厘米。
故答案为:C
【点睛】此题的解题关键是灵活运用三角形和平行四边形的面积公式以及它们之间的关系求解。
2.D
【分析】根据求组合图形的面积的方法,用“割补法”把组合图形割成几个不同的图形或补成其它的图形,据此逐一分析各项即可。
【详解】A.把这个组合图形补成一个长方形,此时该图形的面积等于长方形的面积减去梯形的面积,列式为:10×12-(7+12)×(10-8)÷2,不符合题意;
B.把该图形割成一个三角形和一个长方形,此时该图形的面积等于三角形的面积加上长方形的面积,列式为:12×8+(12-7)×(10-8)÷2,不符合题意;
C.把该图形割成一个梯形和一个长方形,此时该图形的面积等于梯形的面积加上长方形的面积,列式为:7×8+(8+10)×(12-7)÷2,不符合题意;
D.把该图形割成一个三角形和一个梯形,此时该图形的面积等于三角形的面积加上梯形的面积,列式为:(7+12)×8÷2+10×(12-7)÷2,符合题意;
故答案为:D
【点睛】本题考查组合图形的面积,明确运用“割补法”是解题的关键。
3.B
【分析】把一个长方形框架拉成平行四边形,长方形的长=平行四边形的底,长方形的宽>平行四边形的高,据此分析。
【详解】根据分析,把一个长方形框架拉成平行四边形,长方形面积=长×宽>平行四边形的底×高=平行四边形面积,面积变小了是因为高变短了。
故答案为:B
【点睛】关键是熟悉长方形和平行四边形的特征,掌握并灵活运用平行四边形面积公式。
4.B
【分析】A.根据三角形的面积=底×高÷2,据此列出方程;
B.根据题意可得等量关系:每个小朋友分得的支数×小朋友的人数=铅笔的总支数,据此列出方程;
C.根据题意可得等量关系:小芳课外书的本数+4=小明课外书的本数,据此列出方程;
D.根据题意可得等量关系:4天看的总页数÷4=平均每天看的页数,据此列出方程。
【详解】A.设高为米,列方程为:4÷2=24,不符合题意;
B.设每个小朋友分得支,列方程为:4=24,符合题意;
C.设小芳有本课外书,列方程为:+4=24,不符合题意;
D.设小明4天可以看页,列方程为:÷4=24,不符合题意。
故答案为:B
【点睛】本题考查列方程解决问题,从题目中找到等量关系,按等量关系列出方程。
5.B
【分析】平行四边形面积=底×高,注意公式中的底和高指的是对应的一组底和高,据此分析。
【详解】2×2.4=4.8(平方厘米)
3×1.6=4.8(平方厘米)
所以列式正确的选项为①③。
故答案为:B
【点睛】关键是掌握并灵活运用平行四边形面积公式。
6.B
【分析】估计不规则图形的面积时,可以根据图形的特点转化成已学过的图形,再利用面积公式来估算面积。
【详解】将叶子的形状近似地看成平行四边形,如下图,底是5cm,高是6cm。
根据平行四边形的面积=底×高计算,5×6=30(cm2),所以这片叶子的面积约是30cm2。
故答案为:B
【点睛】估计不规则图形的面积也可以用数方格的方法,不满一格的都按半格计算。
7.B
【分析】三角形的面积=底×高÷2,则底=面积×2÷高,据此解答即可。
【详解】60×2÷12
=120÷12
=10(cm)
与这条高对应的底是10cm。
故答案为:B
【点睛】此题主要考查三角形面积的计算方法的灵活应用。
8.C
【分析】根据三角形周长=三条线段的长度和;梯形面积=(上底十下底)×高÷2,分别表示出三角形的周长,梯形的面积,总钱数以及线段的长度,再选择即可。
【详解】A.三角形的周长x+x+6=2x+6;
B.梯形的面积(x+6+x)×2÷2
=(2x+6)×2÷2
=2x+6;
C.线段的总长度2+x+6=x+8;
D.两人的总钱数x+6+x=2x+6。
故答案为:C
【点睛】此题考查了用字母表示数的方法,关键是弄清题中字母所表示的意义,再进一步解答。
9. 12 162
【分析】一腰垂直于底的梯形叫直角梯形。梯形的上底为9厘米,下底为18厘米,则梯形的高为12厘米;根据梯形的面积=(上底+下底)×高÷2,代入数据即可求出梯形的面积。
【详解】梯形的高是12厘米。
(9+18)×12÷2
=27×12÷2
=162(平方厘米)
即梯形的面积是162平方厘米。
【点睛】此题的解题关键是理解掌握梯形的特征以及梯形的面积的计算方法。
10.10.4
【分析】由“三角形的面积=底×高÷2”可得“三角形的高=三角形的面积×2÷底”,三角形的面积和底已知,代入关系式即可求解。
【详解】15.6×2÷3
=31.2÷3
=10.4(厘米)
所以,这个三角形的高是10.4厘米。
【点睛】此题主要考查三角形的面积的计算方法的灵活应用。
11. 20 12
【分析】三角形的面积=底×高÷2;一个因数不变,另一个因数扩大到原来的几倍或缩小到原来的几分之一(0除外),积也扩大到原来几倍或缩小到原来的几分之一;如果一个因数扩大到原来几倍或缩小到原来的几分之一,另一个因数反而缩小到原来的几分之一或扩大到相同的倍数(0除外),那么积不变。据此解答。
【详解】20×2÷2=20(平方厘米)
20÷2×1.2=12(平方厘米)
一个面积是20平方厘米的三角形,如果把它的底扩大到原来的2倍,高缩小到原来的一半,那么变化后三角形的面积是20平方厘米;如果把它的底缩小到原来的一半,高扩大到原来的1.2倍,那么变化后三角形的面积是12平方厘米。
【点睛】本题考查了三角形面积公式的灵活应用以及积的变化规律。
12.16
【分析】根据梯形的高=面积×2÷上下底的和,列式计算即可。
【详解】200×2÷25=16(m)
它的高是16m。
【点睛】关键是掌握并灵活运用梯形面积公式。
13.192
【分析】根据“平行四边形面积=底×高”可知,平行四边形的底=平行四边形的面积÷高,据此先求出平行四边形的面积,再求出平行四边形另一条边的长度;然后求出平行四边形的周长即可。
【详解】60×30÷50
=1800÷50
=36(米)
(60+36)×2
=96×2
=192(平方米)
所以,篱笆长192米。
【点睛】熟记平行四边形面积、周长计算公式,是解答此题是关键。
14. 7.2 3.6
【分析】先根据平行四边形的面积公式求出平行四边形的面积;再根据三角形的面积是与它等底等高的平行四边形面积的一半,即可求出三角形的面积。
【详解】8×0.9=7.2(平方分米)
平行四边形的面积是7.2平方分米,
7.2÷2=3.6(平方分米)
和它等底等高的三角形的面积是3.6平方分米。
【点睛】解答此题的关键是掌握平行四边形的面积公式以及三角形的面积是和它等底等高的平行四边形面积的一半。
15.320
【分析】因为围花坛的篱笆长52m,由图可知:梯形花坛的高为20m,用“52-20”求出上底和下底的和,进而根据“梯形的面积=(上底+下底)×高÷2”解答即可。
【详解】(52-20)×20÷2
=32×20÷2
=640÷2
=320(m2)
这个花坛的面积是320m2。
【点睛】此题考查的是梯形面积计算公式的运用,理解“52-20”是上底和下底的和是本题的关键。
16.22
【分析】不规则图形的面积估算方法:数格子,分别数出满格和不满格的数量,不满格的数量按半格计算,再加上满格的数量,就是不规则图形的格子数,最后乘每个小方格的面积即可。
【详解】满格有14个,不满格有16个;
一共有:
14+16÷2
=14+8
=22(个)
面积:1×22=22(cm2)
估计这片叶子的面积约是22cm2。
(答案不唯一)
【点睛】掌握不规则图形面积的估算方法是解题的关键。
17.×
【分析】由梯形的面积公式可推导出:梯形的高=梯形的面积×2÷(上底+下底),把梯形的面积、上底和下底的和代入计算出高即可。
【详解】50×2÷10
=100÷10
=10(cm)
10≠5
所以这个梯形的高是10cm。原题说法错误。
故答案为:×
【点睛】计算梯形的面积时,不要忘记除以2。
18.√
【分析】如图所示,连接梯形ABCD的对角线AC,把梯形分成两个等高的三角形,利用“三角形的面积=底×高÷2”表示出三角形ABC和三角形ACD的面积,梯形的面积=三角形ABC的面积+三角形ACD的面积,据此解答。
【详解】
上底×高÷2+下底×高÷2
=上底×(高÷2)+下底×(高÷2)
=(上底+下底)×(高÷2)
=(上底+下底)×高÷2
所以,梯形的面积=(上底+下底)×高÷2。
由上可知,我们在进行梯形面积公式的推导时,也可以把梯形转化成两个三角形进行推导。
故答案为:√
【点睛】熟记三角形的面积计算公式,并掌握梯形面积公式的推导过程是解答题目的关键。
19.×
【分析】把一个平行四边形拉成一个长方形,四边的长度不变,则周长不变,根据平行四边形的面积公式:S=ah,长方形的面积公式:S=ab,把一个平行四边形拉成一个长方形(边长不变),由于长方形的宽大于平行四边形的高,所以拉成长方形的面积大于平行四边形的面积。据此解答。
【详解】因为把平行四边形拉成长方形,四个边的长度没变,则其周长不变;
但是它的高变长了,所以它的面积就变大了。
所以原题说法错误。
故答案为:×
【点睛】本题考查了平行四边形、长方形的特征和性质,理解掌握平行四边形的面积公式、长方形的面积公式的灵活运用,关键是熟记公式。
20.×
【分析】把一个平行四边形框架拉成了一个长方形之后,长方形的宽大于平行四边形的高,长方形的长等于平行四边形的底。所以长方形的面积比原来平行四边形的面积大。
【详解】把一个平行四边形框架拉成了一个长方形之后,长方形的宽大于平行四边形的高,大于5cm,长方形的长等于平行四边形的底是8cm ,所以长方形的面积比原来平行四边形的面积大,原来平行四边形的面积小于40cm2。
故答案为:×
【点睛】解答此题的关键是:把一个平行四边形拉成长方形之后,长方形的宽大于平行四边形的高,长方形的长等于平行四边形的底,最后算出的面积比平行四边形的面积大。
21.80平方厘米
【分析】阴影部分是由一个底为12厘米,高为5厘米的三角形和一个上底为12厘米,下底为8厘米,高为5厘米的梯形组合而成,那么分别利用三角形和梯形的面积公式求出这两个图形的面积,再相加即可求出阴影部分的面积。
【详解】12×5÷2+(12+8)×5÷2
=60÷2+20×5÷2
=30+50
=80(平方厘米)
即阴影部分的面积是80平方厘米。
22.63.7平方米
【分析】观察图形可知,组合图形的面积=三角形的面积+平行四边形的面积,根据三角形的面积=底×高÷2,平行四边形的面积=底×高,代入数据计算求解。
【详解】三角形的面积:
9.8×3÷2
=29.4÷2
=14.7(平方米)
平行四边形的面积:
9.8×5=49(平方米)
一共:14.7+49=63.7(平方米)
组合图形的面积是63.7平方米。
23.见详解
【分析】已知平行四边形、三角形、梯形的面积都是12平方厘米,且高相等;根据平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,由此确定平行四边形的底和高、三角形的底和高、梯形的上底、下底和高,据此画出符合要求的图形。
【详解】平行四边形的面积:3×4=12(平方厘米)
三角形的面积:6×4÷2=12(平方厘米)
梯形的面积:
(2+4)×4÷2
=6×4÷2
=12(平方厘米)
画一个底为3厘米、高为4厘米的平行四边形;
画一个底为6厘米、高为4厘米的三角形;
画一个上底为2厘米、下底为4厘米、高为4厘米的梯形。
如图:
(答案不唯一)
【点睛】本题考查画指定面积的平行四边形、三角形和梯形,掌握平行四边形、三角形、梯形的面积公式是解题的关键。
24.1050平方米
【分析】如图:这块鳄鱼池是由一个长为45米,宽为20米的长方形和一个底为(45-25)米,高为(35-20)米的三角形组合而成,分别利用长方形和三角形的面积公式求出这两个图形的面积,再相加即可得解。
【详解】45×20+(45-25)×(35-20)÷2
=900+20×15÷2
=900+150
=1050(平方米)
答:它的占地面积是1050平方米。
【点睛】此题主要考查组合图形的面积的计算方法,灵活运用长方形和三角形的面积公式求解。
25.1040棵
【分析】根据三角形的面积=底×高÷2,已知这块三角形空地的底边长是40米,高是13米,代入到公式中即可求出这块三角形空地的面积,再除以每棵向日葵占地0.25平方米,即可求出这块地可种多少棵向日葵。
【详解】40×13÷2÷0.25
=520÷2÷0.25
=1040(棵)
答:这块地可种1040棵向日葵。
【点睛】此题的解题关键是灵活运用三角形的面积公式解决实际问题。
26.312.5平方米
【分析】观察图意可知,学校开辟的这块农场总面积=底和高都是15米的三角形面积+底和高都是20米的三角形面积,据此根据“三角形面积=底×高÷2”,即可解题。
【详解】15×15÷2+20×20÷2
=225÷2+400÷2
=112.5+200
=312.5(平方米)
答:学校开辟的这块农场总面积是312.5平方米。
【点睛】熟记三角形面积计算公式,是解答此题的关键。
27.4800平方米;48米
【分析】平均每棵果树占地0.5平方米,那么9600棵树就有9600个0.5,用9600×0.5即可求出这块地的面积;平行四边形的面积=底×高,所以高=面积÷底,代入数据计算即可求解。
【详解】9600×0.5=4800(平方米)
4800÷100=48(米)
答:这块地的面积有4800平方米,底边的高是48米。
【点睛】此题考查小数乘法的计算以及平行四边形面积公式的灵活应用。
28.6千克
【分析】由图意可知:这面墙由1个梯形和1个长方形组成;利用梯形的面积=(上底+下底)×高÷2和长方形的面积=长×宽,求出梯形和长方形的面积,再相加即可求解。
【详解】(4+8)×2÷2+8×3.5
=12×2÷2+28
=24÷2+28
=12+28
=40(平方米)
0.15×40=6(千克).
答:至少需要准备6千克涂料。
【点睛】本题考查的是组合图形的面积,解答此题的关键是:弄清楚这面墙有哪几个图形组成,进而求其面积,问题即可逐步得解。
29.128千克
【分析】根据平行四边形的面积公式:S=ah,据此求出广告牌的面积,再乘2即可求出这块广告牌的正反两面的面积,最后再乘0.8即可。
【详解】12.5×6.4×2×0.8
=80×2×0.8
=160×0.8
=128(千克)
答:共需要128千克防水漆。
【点睛】本题考查平行四边形的面积,熟记公式是解题的关键。
30.514.5元
【分析】先根据梯形的面积=(上底+下底)×高÷2,把数据代入公式求出挡风玻璃的面积,再根据每平方米600元,用单价×面积求出这块玻璃的总价格即可。
【详解】(100+145)×70÷2
=245×70÷2
=17150÷2
=8575(平方厘米)
8575平方厘米=0.8575平方米
600×0.8575=514.5(元)
答:这块玻璃的价格大概是514.5元。
【点睛】掌握梯形面积公式以及经济问题的基本数量关系是解题的关键,计算时要注意单位换算一致。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
