人教版五年级数学上册第四单元可能性同步学案(知识点梳理+能力百分练)二
文档属性
| 名称 | 人教版五年级数学上册第四单元可能性同步学案(知识点梳理+能力百分练)二 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 06:24:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版五年级数学上册第四单元可能性(知识点梳理+能力百分练)二
知识点梳理
1、事件发生有确定性和不确定性,确定事件也就是一定会发生的或一定不会发生的事件,用“一定”、“不可能”来描述,不确定事件用“可能”来描述。
2、在游戏中,我们可以发现事件发生的可能性不同主要是受到了大小,数量,面积等原因,总结来说也就是某种情况在总数中所占比重越多,某一事件发生的可能性就越大。
3、设计与可能性相关的游戏时,先要知道游戏的所有可能性,再根据要求修改各种不同的事件发生的可能性。
能力百分练
一、选择题(共16分)
1.在装有红球、黄球、白球的袋子里,( )摸出绿球。
A.可能 B.一定能 C.不可能 D.不确定
2.把下面四张扑克牌反扣在桌面上,并把它们的次序打乱,任意摸一张。下面说法错误的是( )。
A.摸到9的可能性最大
B.摸到9的可能性比7大
C.摸到7和10的可能性一样大
D.摸到7、9和10的可能性一样大
3.李明做摸球游戏,他任意摸了200次,摸到红球42次,黄球158次。根据数据推测,他最有可能是在装有( )的盒子里摸的。
A.10个红球 B.8个红球2个黄球
C.2个红球8个黄球 D.10个黄球
4.从一副扑克牌中任意抽出一张,那么抽出的一张中,( )。
A.是大王或小王的可能性最小 B.是梅花或方块的可能性大些
C.是红桃或黑桃的可能性大些 D.是大小王、梅花、方块、红桃、黑桃的可能性一样大
5.指针停在阴影区域可能性最大的是( )。
A. B. C.D.
6.袋子里有两种颜色的球(除颜色外完全相同),妙妙从中摸出一个球后再放回去摇匀,这样重复摸了50次,摸球的情况如下表,下列说法错误的是( )。
黄球 红球
次数 8 42
A.袋子里红球可能多。
B.如果再摸一次,摸到红球的可能性大。
C.袋子里黄球可能少。
D.如果再摸一次,摸到的一定是红球。
7.把一个转盘10等分,红色涂3份,黄色涂5份,剩下的涂蓝色,转动转盘,指针指向( )的可能性最大。
A.黄色 B.红色 C.蓝色 D.不确定
8.如图,把一个均匀的圆形转盘等分成8份,在每一份上涂上红、黄、蓝、绿四种颜色中的一种,再安装上指针,设计成一个“幸运大转盘”。任意转动转盘,指针停留在( )区域的可能性最大。
A.红色 B.黄色 C.蓝色 D.绿色
二、填空题(共16分)
9.把2个红球和3个黄球同装在一个箱子里,任意摸出一个球,摸到( )球的可能性大一些。
10.袋子里有红球10个,黄球5个,摸到( )球的可能性大,( )摸到白球。
11.如图,同时掷两个骰子,得到的两个数中,和最大是( ),最小是( )。
12.国庆节期间,某超市开展有奖购物活动,规定凡购物满50元者均可参加刮奖,设一等奖1名,二等奖3名,三等奖10名,纪念奖100名。妈妈10月1日购物58元,她去刮奖,最有可能刮中( )奖。
13.在一个既有黑球又有白球的袋子里,任意摸出一个球,可能是( ),也可能是( )。
14.一个放有2个白球和6个红球、8个黄球的盒子里,任意摸出一个球,摸出( )球的可能性最大,摸到( )球的可能性最小。
15.五年级一班一组的10个同学抽签表演节目,其中有6张是讲故事,3张是唱歌,1张是跳舞,小红抽一次,可能出现( )种结果。
16.果盘里有6个橙子,3个橘子,8个苹果,周星星同学随便拿出一个水果,拿到( )的可能性最小,要想拿到这种水果的可能性最大,至少还要加( )个这种水果。
三、判断题(共8分)
17.希望小学每年都举行校园足球联赛,连续四届五(5)班都是冠军,今年五(5)班一定是冠军。( )
18.盒子里有100粒黄珠子,1粒红珠子,任意拿一粒,不可能拿到红珠子。( )
19.转动如图的转盘,指针停在白色部分的可能性大。( )
20.袋子里装有一些大小相同的1个白球和6个红球,任意摸一个球(摸出后不放回)。小乐第一次摸到了白球,第二次一定摸到红球。( )
四、连线题(共12分)
21.(6分)下图第一排是一些可以自由转动的转盘,将它们分别转动4次后,请你用第二排的语言描述转出最大四位数可能性的大小,并用线连起来。
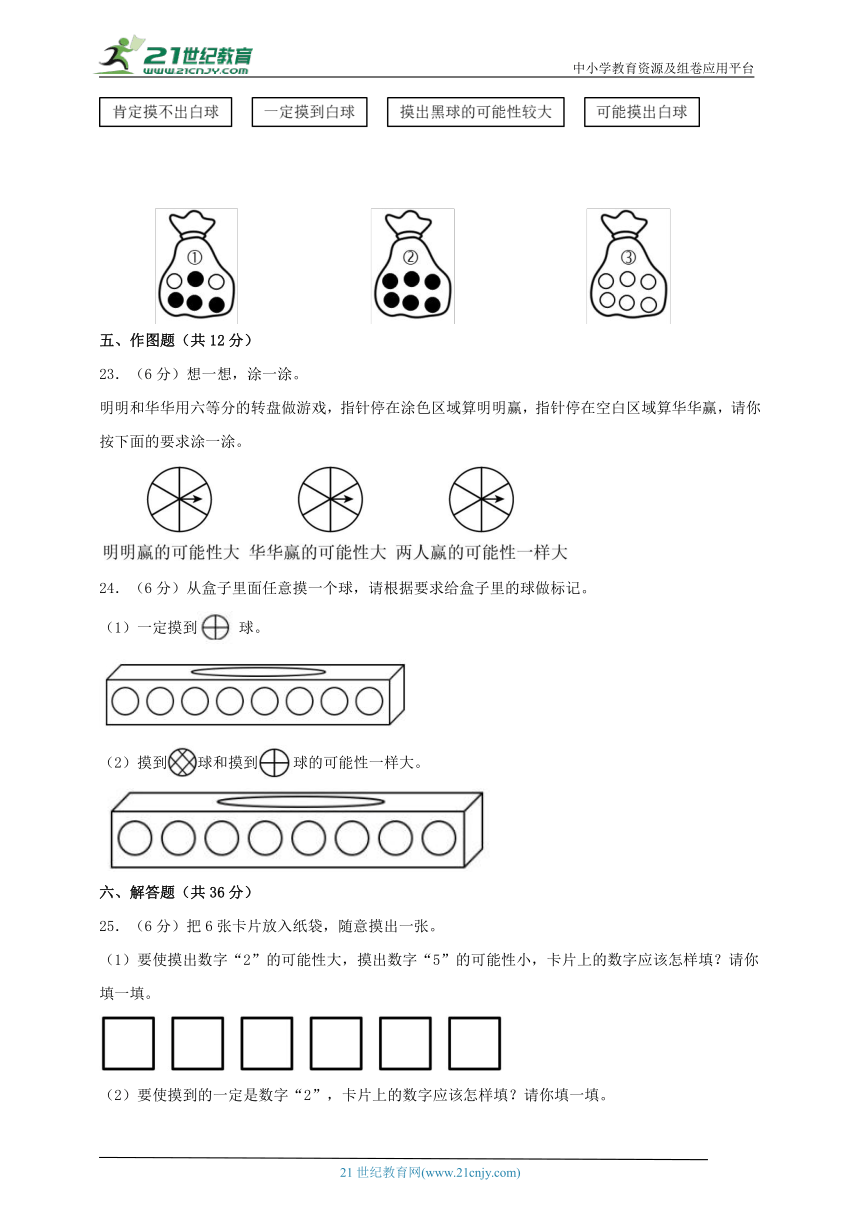
22.(6分)袋子里的球除颜色外完全相同,从中任意摸出一个球,结果会怎样?连一连。
五、作图题(共12分)
23.(6分)想一想,涂一涂。
明明和华华用六等分的转盘做游戏,指针停在涂色区域算明明赢,指针停在空白区域算华华赢,请你按下面的要求涂一涂。
24.(6分)从盒子里面任意摸一个球,请根据要求给盒子里的球做标记。
(1)一定摸到球。
(2)摸到球和摸到球的可能性一样大。
六、解答题(共36分)
25.(6分)把6张卡片放入纸袋,随意摸出一张。
(1)要使摸出数字“2”的可能性大,摸出数字“5”的可能性小,卡片上的数字应该怎样填?请你填一填。
(2)要使摸到的一定是数字“2”,卡片上的数字应该怎样填?请你填一填。
26.(6分)分别从下面两个盒子里摸棋子。
(1)哪个盒子里肯定能摸出红棋子?
(2)哪个盒子里可能摸出绿棋子?
(3)哪个盒子里不可能摸出绿棋子?
27.(6分)现在是上午9时,外面正下着大雨。小松说“:再过14小时,太阳一定会出来。”他说的可能发生吗?
28.(6分)明明和小丽两人都有写着数字2,5,6,8的卡片各一张。每人拿出一张卡片,若两数的和是双数,则聪聪获胜;若两数的和是单数,则亮亮获胜。谁获胜的可能性大?你能换掉一张卡片使游戏更公平吗?
29.(6分)为庆祝神舟十三号载人飞船发射成功,学校购买了部分飞船模型拼装玩具。淘气班举办了“幸运转盘赢模型”的游戏,老师将为赢得游戏的同学发飞船模型拼装玩具。你认为这个游戏规则公平吗?请你设计一个公平的游戏规则。
30.(6分)淘气和笑笑下跳棋。笑笑准备了一些卡片(如下图),她设计的游戏规则是任意摸一张卡片,卡片上的点数大于5笑笑先走,点数小于5淘气先走。这个游戏规则公平吗?请写出你判断的理由。
参考答案
1.C
【分析】根据题意,在装有红球、黄球、白球的袋子里,没有绿球,所以不可能摸出绿球。
【详解】在装有红球、黄球、白球的袋子里,不可能摸出绿球。
故答案为:C
【点睛】本题考查可能性的知识,判断事件发生的可能性的几种情况:可能、不可能、一定;在任何情况下,都不会发生的事件,是“不可能”事件。
2.D
【分析】从图中可知,9有2张,7有1张,10有1张;根据可能性大小的判断方法,数量最多的,摸到的可能性最大;反之,数量最少的,摸到的可能性就最小;数量相等的,摸到的可能性一样大。
【详解】A.9的张数最多,所以摸到9的可能性最大,原题说法正确;
B.9的张数比7的张数多,所以摸到9的可能性比7大,原题说法正确;
C.7和10的张数一样多,所以摸到7和10的可能性一样大,原题说法正确;
D.7、9、10的张数不一样多,所以摸到7、9和10的可能性不一样大,原题说法错误。
故答案为:D
【点睛】本题考查可能性的大小,根据事件数量的多少判断可能性的大小。
3.C
【分析】逐项分析,根据条件判断可能性,用排除法求解。
【详解】A. 10个红球,不可能摸到黄球,不符合;
B. 8个红球2个黄球,红球多,摸到红球的可能性比黄球要大,不符合;
C. 2个红球8个黄球,黄球多,摸到黄球的可能性比红球要大,符合;
D. 10个黄球,不可能摸到红球,不符合。
故答案为:C
【点睛】本题主要考查可能性在生活中的应用。
4.A
【分析】一副扑克牌一共有54张,大王小王各1张,剩下的52张中梅花、方块、红桃、黑桃各13张,哪种花色的扑克牌数量越多,抽到的可能性就越大,哪种花色的扑克牌数量越少,抽到的可能性就越小,据此解答。
【详解】分析可知,一副扑克牌中大王或小王的数量最少,抽到大王或小王的可能性最小,梅花、方块、红桃、黑桃的数量相同,抽到梅花、方块、红桃、黑桃的可能性一样大。
故答案为:A
【点睛】根据各种花色扑克牌数量的多少判断事件发生可能性的大小是解答题目的关键。
5.A
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。已知圆被平均分成了4份,观察每个选项阴影部分有几份,再比较,数量越多,指针指到的可能性越大。
【详解】圆被平均分成了4份,阴影部分有3份,阴影部分有1份,阴影部分有2份,阴影部分有2份;
3>2>1
所以指针停在阴影区域可能性最大的是。
故答案为:A
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
6.D
【分析】可能性的大小与数量的多少有关,数量多则被摸到的可能性就大,反之就小。据此选择即可。
【详解】A.因为红球摸的次数多,所以袋子里红球可能多;
B.因为袋子里红球多,所以如果再摸一次,摸到红球的可能性大。
C.因为黄球摸的次数少,所以袋子里红球可能少;
D.因为袋子里既有红球,又有黄球,所以如果再摸一次,摸到的不一定是红球。
故答案为:D
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
7.A
【分析】由题可知,把一个转盘10等分,红色涂3份,黄色涂5份,蓝色则占10-3-5=2份,然后根据数量多的可能性就大来解答即可。
【详解】蓝色:10-3-5
=7-5
=2
2<3<5
所以指针指向黄色的可能性最大。
故答案为:A
【点睛】解决此题关键是根据不需要准确地计算可能性的大小时,可以根据所占份数的多少,直接判断可能性的大小。
8.D
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。根据题意,“幸运大转盘”中红色区域有2份、黄色区域有2份、蓝色区域有1份、绿色区域有3份,绿色区域最多,所以任意转动转盘,指针停留在绿色区域的可能性最大,据此解答。
【详解】“幸运大转盘”中红色区域有2份、黄色区域有2份、蓝色区域有1份、绿色区域有3份,3>2>1,绿色最多,所以任意转动转盘,指针停留在绿色区域的可能性最大。
故答案为:D
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
9.黄
【分析】根据可能性大小的判断方法,比较箱子里红球、黄球的数量,哪种颜色球的数量多,摸到的可能性就大。
【详解】3>2
黄球的数量多,所以任意摸出一个球,摸到黄球的可能性大一些。
【点睛】本题考查可能性的大小,根据事件数量的多少判断可能性的大小。
10. 红 不可能
【分析】事件发生的可能性大小是不确定的,当数量相对较多时,它发生的可能性就大;反之数量相对较少时,可能性就小。无论在什么情况下,都会发生的事件,是“一定”会发生的事件。在任何情况下,都不会发生的事件,是“不可能”事件。在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。
【详解】10>5
红球的数量比黄球的数量多,所以摸到红球的可能性大;
袋子里面没有白球,所以不可能摸到白球。
【点睛】此题主要考查事件的确定性与不确定性以及可能性的大小,明确可能性的大小与数量的多少有关是解题的关键。
11. 12 2
【分析】每个骰子六个面上分别写着数字1~6,要使两个朝上的数字相加,和最小,只需每个骰子投出的数字最小。要使两个朝上的数字相加,和最大,只需每个骰子投出的数字最大。
【详解】6+6=12
1+1=2
即和最大是12,最小是2。
【点睛】两个加数最小时,它们的和最小;两个加数最大时,它们的和最大。
12.纪念
【分析】根据题意可知,妈妈购物58元,超过50元,可参加刮奖。因为奖项中一等奖1名,二等奖3名,三等奖10名,纪念奖100名,事件发生的可能性大小是不确定的,当数量相对较多时,它发生的可能性就大;反之数量相对较少时,可能性就小。纪念奖最多,所以妈妈最有可能刮到纪念奖。
【详解】1<3<10<100
即妈妈最有可能刮中纪念奖。
【点睛】此题考查可能性的大小,刮奖活动中,数量多的奖项刮中的可能性就大,根据日常生活经验判断。
13. 黑球 白球
【分析】袋子里有几种颜色的球,从袋子里摸出球的可能性就有几种,哪种颜色球的数量越多,摸出该种颜色球的可能性就越大,哪种颜色球的数量越少,摸出该种颜色球的可能性就越小,据此解答。
【详解】分析可知,袋子里既有黑球又有白球,从袋子里任意摸出一个球,可能是黑球,也可能是白球。
【点睛】理解摸出球的可能性与袋子里球的颜色有关是解答题目的关键。
14. 黄 白
【分析】可能性的大小与球数量的多少有关,数量多则被摸到的可能性就大,反之就小。据此解答即可。
【详解】因为8>6>2
则任意摸出一个球,摸出黄球的可能性最大,摸到白球的可能性最小。
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
15.3
【分析】根据题意卡片上写着讲故事、唱歌和跳舞,小红抽一次,可能是讲故事、也可能是唱歌或跳舞。
【详解】据分析可知,小红抽一次,可能是讲故事、也可能是唱歌或跳舞,也就是可能出现3种结果。
【点睛】本题考查了可能性知识,结合题意进行分析即可。
16. 橘子 6
【分析】(1)因为果盘里有6个橙子,3个橘子,8个苹果,8>6>3,所以从果盘里任意摸出一个水果,摸到橘子的可能性最小;
(2)要想让这种水果的可能性最大,至少还要加8+1-3=6(个),据此进行填空。
【详解】果盘里有6个橙子,3个橘子,8个苹果,周星星同学随便拿出一个水果,拿到(橘子)的可能性最小,要想拿到这种水果的可能性最大,至少还要加(6)个这种水果。
【点睛】解决此题关键是根据不需要准确地计算可能性的大小时,可以根据各种水果个数的多少,直接判断可能性的大小。
17.×
【分析】无论在什么情况下,都会发生的事件,是“一定”会发生的事件。在任何情况下,都不会发生的事件,是“不可能”事件。在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。据此解答。
【详解】虽然连续四届五(5)班都是冠军,但今年五(5)班能不能得冠军并不确定,所以今年五(5)班可能是冠军,题干中的说法是错误的。
故答案为:×
【点睛】此题主要考查事件的确定性与不确定性,对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。
18.×
【分析】如果盒子里只有红珠子,任意拿一粒,拿到的一定是红珠子;如果盒子里除了红珠子还有其它颜色的珠子,任意拿一粒,可能拿到红珠子,也可能拿到其它颜色的珠子;如果盒子里没有红珠子,任意拿一粒,不可能拿到红珠子,据此解答。
【详解】由题意可知,盒子里有黄珠子和红珠子两种颜色的珠子,任意拿一粒,可能拿到黄珠子,也可能拿到红珠子。
故答案为:×
【点睛】准确地用“一定”“可能”“不可能”等词语来描述事件发生的可能性是解答题目的关键。
19.×
【分析】比较白色部分和阴影部分,哪一部分所占的区域大,指针停在哪种区域的可能性就大;如果两部分区域一样大,则指针停在两部分的可能性一样大,据此分析。
【详解】由于图中白色部分与阴影部分相等,所以转动转盘,指针停在白色部分和阴影部分的可能性相等,原题说法错误。
故答案为:×
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种颜色的区域大,发生的可能性就大一些。
20.√
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。袋子里装有1个白球和6个红球,第一次摸了白球,摸出后不放回袋子里,则余下的全部是红球,第二次一定摸到红球;据此回答。
【详解】袋子里装有一些大小相同的1个白球和6个红球,第一次摸到白球后,不放回,袋子里剩下都是红球,所以第二次一定摸到红球。原题干说法正确。
故答案为:√
【点睛】解决此类问题的关键是分两种情况:(1)需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可;(2)不需要计算可能性的大小的准确值时,可以根据各种球数量的多少,直接判断可能性的大小。
21.见详解
【分析】最大的四位数是9999。
第一个转盘内没有9,那么不可能转出最大的四位数;
第二个转盘内只有一个9,转出最大的四位数的可能性比较小;
第三个转盘内有9个9,1个0,很有可能转出最大的四位数;
第四个转盘内有3个9,可能转出最大的四位数;
第五个转盘内全部是9,一定能转出最大的四位数。
【详解】第一个转盘不可能转出最大的四位数;
第二个转盘不太可能转出最大的四位数;
第三个转盘很可能转出最大的四位数;
第四个转盘可能转出最大的四位数;
第五个转盘一定能转出最大的四位数。
连线如下:
【点睛】本题考查了可能性的大小,掌握可能性大小的判断方法是解题的关键。
22.见详解
【分析】袋子里没有白球,肯定摸不出白球;袋子里全是白球,一定摸到白球;有白球有黑球,黑球数量多,摸出黑球的可能性较大;袋子里有白球也有其它球,可能摸出白球,据此连线。
【详解】
【点睛】哪种球的数量多,发生的可能性就大一些。对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。
23.见详解
【分析】根据各种区域面积的大小,直接判断可能性的大小;如果明明赢的可能性大,则涂色区域的面积大;反之,如果华华赢的可能性大则白色区域的面积大;如果使游戏最公平,则应把两种颜色的区域涂得面积相等;据此涂色即可。
【详解】如图:
(涂法不唯一)
【点睛】本题考查可能性的大小,解决此类问题的关键是分两种情况:(1)需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答;(2)不需要计算可能性的大小的准确值时,可以根据各种区域面积的大小,直接判断可能性的大小。
24.(1)见详解;(2)见详解
【分析】(1)根据“一定摸到球”,说明这个盒子里面的球全部是球。
(2)根据“摸到球和摸到球的可能性一样大”,说明两种球一样多。
【详解】(1)一定摸到球,如图:
(2)摸到球和摸到球的可能性一样大,如图:
【点睛】正确理解“一定”、“可能”、“不可能”表示的含义,根据这个含义求解。
25.(1)(2)见详解
【分析】(1)事件发生的可能性大小是不确定的,当数量相对较多时,它发生的可能性就大;反之数量相对较少时,可能性就小。要使摸出数字“2”的可能性大,摸出数字“5”的可能性小,卡片上填数字“2”的数量比填数字“5”的数量多即可满足条件。
(2)无论在什么情况下,都会发生的事件,是“一定”会发生的事件。要使摸到的一定是数字“2”,那么卡片里数字都要填数字“2”,不能填其它的数,即可满足条件。
【详解】(1)填数如下:
或者
(2)填数如下:
【点睛】本题考查可能性的大小以及事件的确定性与不确定性,明确可能性的大小与数量的多少有关是解题的关键。
26.(1)左边
(2)右边
(3)左边
【分析】(1)盒子里全是红棋子,肯定能摸出红棋子。
(2)盒子里只要有绿棋子,且还有其它颜色的棋子,可能摸出绿棋子。
(3)盒子里没有绿棋子,不可能摸出绿棋子。
【详解】(1)左边盒子里肯定能摸出红棋子。
(2)右边盒子里可能摸出绿棋子。
(3)左边盒子里不可能摸出绿棋子。
【点睛】对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。
27.一定不可能发生
【分析】事件的确定性:“一定”表示确定事件,“可能”表示不确定事件,“不可能”属于确定事件中的必然事件,结合实际生活,按要求写出即可。
【详解】9+14=23(时)
上午9时,再过14小时,正好是23时,是深夜,一定不会有太阳出来,因此小松说的一定不可能发生。
【点睛】此题考查的是事件的确定性和不确定性,应明确事件的确定性和不确定性,并能结合实际进行正确判断。
28.聪聪;见详解
【分析】先计算出两数的和的所有情况,再看和是双数、单数分别有几种情况,哪种情况出现越多,获胜的可能性就越大。
因为数字2,5,6,8中双数多,单数少,所以要用单数替换掉其中的一张双数的卡片,让游戏更公平。
【详解】两数的和:
2+2=4, 2+5=7,2+6=8,2+8=10;
5+2=7,5+5=10,5+6=11,5+8=13;
6+2=8,6+5=11,6+6=12,6+8=14;
8+2=10,8+5=13,8+6=14,8+8=16;
一共有16种情况,和为双数的有10种情况,和为单数的有6种情况;
10>6,所以聪聪获胜的可能大。
因为单数+单数=双数,双数+双数=双数,单数+双数=单数,所以把其中一张双数卡片换成单数卡数,和出现单数和双数的可能性相等,两人获胜的可能性相等。
答:聪聪获胜的可能大。把写着数字2的卡片都换成写着数字3的卡片,这样游戏更公平。(方法不唯一)
【点睛】本题考查可能性的大小以及游戏的公平性,要使游戏公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
29.不公平;公平的游戏规则见详解
【分析】确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
【详解】小于5的数有1、2、3、4,共4种情况,等于或大于5的数有5、6、7、8、9、10,共6种情况,所以游戏规则不公平。
可以指针指向单数的得模型,指针指向双数的不得模型。(答案不唯一)
【点睛】游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。
30.不公平;点数大于5的比点数小于5的多
【分析】确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
【详解】点数大于5的有:8、9、7、6、10,共5个。
点数小于5的有:4、2、3、1,共4个。
这个游戏规则不公平,因为点数大于5的比点数小于5的多。
【点睛】游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版五年级数学上册第四单元可能性(知识点梳理+能力百分练)二
知识点梳理
1、事件发生有确定性和不确定性,确定事件也就是一定会发生的或一定不会发生的事件,用“一定”、“不可能”来描述,不确定事件用“可能”来描述。
2、在游戏中,我们可以发现事件发生的可能性不同主要是受到了大小,数量,面积等原因,总结来说也就是某种情况在总数中所占比重越多,某一事件发生的可能性就越大。
3、设计与可能性相关的游戏时,先要知道游戏的所有可能性,再根据要求修改各种不同的事件发生的可能性。
能力百分练
一、选择题(共16分)
1.在装有红球、黄球、白球的袋子里,( )摸出绿球。
A.可能 B.一定能 C.不可能 D.不确定
2.把下面四张扑克牌反扣在桌面上,并把它们的次序打乱,任意摸一张。下面说法错误的是( )。
A.摸到9的可能性最大
B.摸到9的可能性比7大
C.摸到7和10的可能性一样大
D.摸到7、9和10的可能性一样大
3.李明做摸球游戏,他任意摸了200次,摸到红球42次,黄球158次。根据数据推测,他最有可能是在装有( )的盒子里摸的。
A.10个红球 B.8个红球2个黄球
C.2个红球8个黄球 D.10个黄球
4.从一副扑克牌中任意抽出一张,那么抽出的一张中,( )。
A.是大王或小王的可能性最小 B.是梅花或方块的可能性大些
C.是红桃或黑桃的可能性大些 D.是大小王、梅花、方块、红桃、黑桃的可能性一样大
5.指针停在阴影区域可能性最大的是( )。
A. B. C.D.
6.袋子里有两种颜色的球(除颜色外完全相同),妙妙从中摸出一个球后再放回去摇匀,这样重复摸了50次,摸球的情况如下表,下列说法错误的是( )。
黄球 红球
次数 8 42
A.袋子里红球可能多。
B.如果再摸一次,摸到红球的可能性大。
C.袋子里黄球可能少。
D.如果再摸一次,摸到的一定是红球。
7.把一个转盘10等分,红色涂3份,黄色涂5份,剩下的涂蓝色,转动转盘,指针指向( )的可能性最大。
A.黄色 B.红色 C.蓝色 D.不确定
8.如图,把一个均匀的圆形转盘等分成8份,在每一份上涂上红、黄、蓝、绿四种颜色中的一种,再安装上指针,设计成一个“幸运大转盘”。任意转动转盘,指针停留在( )区域的可能性最大。
A.红色 B.黄色 C.蓝色 D.绿色
二、填空题(共16分)
9.把2个红球和3个黄球同装在一个箱子里,任意摸出一个球,摸到( )球的可能性大一些。
10.袋子里有红球10个,黄球5个,摸到( )球的可能性大,( )摸到白球。
11.如图,同时掷两个骰子,得到的两个数中,和最大是( ),最小是( )。
12.国庆节期间,某超市开展有奖购物活动,规定凡购物满50元者均可参加刮奖,设一等奖1名,二等奖3名,三等奖10名,纪念奖100名。妈妈10月1日购物58元,她去刮奖,最有可能刮中( )奖。
13.在一个既有黑球又有白球的袋子里,任意摸出一个球,可能是( ),也可能是( )。
14.一个放有2个白球和6个红球、8个黄球的盒子里,任意摸出一个球,摸出( )球的可能性最大,摸到( )球的可能性最小。
15.五年级一班一组的10个同学抽签表演节目,其中有6张是讲故事,3张是唱歌,1张是跳舞,小红抽一次,可能出现( )种结果。
16.果盘里有6个橙子,3个橘子,8个苹果,周星星同学随便拿出一个水果,拿到( )的可能性最小,要想拿到这种水果的可能性最大,至少还要加( )个这种水果。
三、判断题(共8分)
17.希望小学每年都举行校园足球联赛,连续四届五(5)班都是冠军,今年五(5)班一定是冠军。( )
18.盒子里有100粒黄珠子,1粒红珠子,任意拿一粒,不可能拿到红珠子。( )
19.转动如图的转盘,指针停在白色部分的可能性大。( )
20.袋子里装有一些大小相同的1个白球和6个红球,任意摸一个球(摸出后不放回)。小乐第一次摸到了白球,第二次一定摸到红球。( )
四、连线题(共12分)
21.(6分)下图第一排是一些可以自由转动的转盘,将它们分别转动4次后,请你用第二排的语言描述转出最大四位数可能性的大小,并用线连起来。
22.(6分)袋子里的球除颜色外完全相同,从中任意摸出一个球,结果会怎样?连一连。
五、作图题(共12分)
23.(6分)想一想,涂一涂。
明明和华华用六等分的转盘做游戏,指针停在涂色区域算明明赢,指针停在空白区域算华华赢,请你按下面的要求涂一涂。
24.(6分)从盒子里面任意摸一个球,请根据要求给盒子里的球做标记。
(1)一定摸到球。
(2)摸到球和摸到球的可能性一样大。
六、解答题(共36分)
25.(6分)把6张卡片放入纸袋,随意摸出一张。
(1)要使摸出数字“2”的可能性大,摸出数字“5”的可能性小,卡片上的数字应该怎样填?请你填一填。
(2)要使摸到的一定是数字“2”,卡片上的数字应该怎样填?请你填一填。
26.(6分)分别从下面两个盒子里摸棋子。
(1)哪个盒子里肯定能摸出红棋子?
(2)哪个盒子里可能摸出绿棋子?
(3)哪个盒子里不可能摸出绿棋子?
27.(6分)现在是上午9时,外面正下着大雨。小松说“:再过14小时,太阳一定会出来。”他说的可能发生吗?
28.(6分)明明和小丽两人都有写着数字2,5,6,8的卡片各一张。每人拿出一张卡片,若两数的和是双数,则聪聪获胜;若两数的和是单数,则亮亮获胜。谁获胜的可能性大?你能换掉一张卡片使游戏更公平吗?
29.(6分)为庆祝神舟十三号载人飞船发射成功,学校购买了部分飞船模型拼装玩具。淘气班举办了“幸运转盘赢模型”的游戏,老师将为赢得游戏的同学发飞船模型拼装玩具。你认为这个游戏规则公平吗?请你设计一个公平的游戏规则。
30.(6分)淘气和笑笑下跳棋。笑笑准备了一些卡片(如下图),她设计的游戏规则是任意摸一张卡片,卡片上的点数大于5笑笑先走,点数小于5淘气先走。这个游戏规则公平吗?请写出你判断的理由。
参考答案
1.C
【分析】根据题意,在装有红球、黄球、白球的袋子里,没有绿球,所以不可能摸出绿球。
【详解】在装有红球、黄球、白球的袋子里,不可能摸出绿球。
故答案为:C
【点睛】本题考查可能性的知识,判断事件发生的可能性的几种情况:可能、不可能、一定;在任何情况下,都不会发生的事件,是“不可能”事件。
2.D
【分析】从图中可知,9有2张,7有1张,10有1张;根据可能性大小的判断方法,数量最多的,摸到的可能性最大;反之,数量最少的,摸到的可能性就最小;数量相等的,摸到的可能性一样大。
【详解】A.9的张数最多,所以摸到9的可能性最大,原题说法正确;
B.9的张数比7的张数多,所以摸到9的可能性比7大,原题说法正确;
C.7和10的张数一样多,所以摸到7和10的可能性一样大,原题说法正确;
D.7、9、10的张数不一样多,所以摸到7、9和10的可能性不一样大,原题说法错误。
故答案为:D
【点睛】本题考查可能性的大小,根据事件数量的多少判断可能性的大小。
3.C
【分析】逐项分析,根据条件判断可能性,用排除法求解。
【详解】A. 10个红球,不可能摸到黄球,不符合;
B. 8个红球2个黄球,红球多,摸到红球的可能性比黄球要大,不符合;
C. 2个红球8个黄球,黄球多,摸到黄球的可能性比红球要大,符合;
D. 10个黄球,不可能摸到红球,不符合。
故答案为:C
【点睛】本题主要考查可能性在生活中的应用。
4.A
【分析】一副扑克牌一共有54张,大王小王各1张,剩下的52张中梅花、方块、红桃、黑桃各13张,哪种花色的扑克牌数量越多,抽到的可能性就越大,哪种花色的扑克牌数量越少,抽到的可能性就越小,据此解答。
【详解】分析可知,一副扑克牌中大王或小王的数量最少,抽到大王或小王的可能性最小,梅花、方块、红桃、黑桃的数量相同,抽到梅花、方块、红桃、黑桃的可能性一样大。
故答案为:A
【点睛】根据各种花色扑克牌数量的多少判断事件发生可能性的大小是解答题目的关键。
5.A
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。已知圆被平均分成了4份,观察每个选项阴影部分有几份,再比较,数量越多,指针指到的可能性越大。
【详解】圆被平均分成了4份,阴影部分有3份,阴影部分有1份,阴影部分有2份,阴影部分有2份;
3>2>1
所以指针停在阴影区域可能性最大的是。
故答案为:A
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
6.D
【分析】可能性的大小与数量的多少有关,数量多则被摸到的可能性就大,反之就小。据此选择即可。
【详解】A.因为红球摸的次数多,所以袋子里红球可能多;
B.因为袋子里红球多,所以如果再摸一次,摸到红球的可能性大。
C.因为黄球摸的次数少,所以袋子里红球可能少;
D.因为袋子里既有红球,又有黄球,所以如果再摸一次,摸到的不一定是红球。
故答案为:D
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
7.A
【分析】由题可知,把一个转盘10等分,红色涂3份,黄色涂5份,蓝色则占10-3-5=2份,然后根据数量多的可能性就大来解答即可。
【详解】蓝色:10-3-5
=7-5
=2
2<3<5
所以指针指向黄色的可能性最大。
故答案为:A
【点睛】解决此题关键是根据不需要准确地计算可能性的大小时,可以根据所占份数的多少,直接判断可能性的大小。
8.D
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。根据题意,“幸运大转盘”中红色区域有2份、黄色区域有2份、蓝色区域有1份、绿色区域有3份,绿色区域最多,所以任意转动转盘,指针停留在绿色区域的可能性最大,据此解答。
【详解】“幸运大转盘”中红色区域有2份、黄色区域有2份、蓝色区域有1份、绿色区域有3份,3>2>1,绿色最多,所以任意转动转盘,指针停留在绿色区域的可能性最大。
故答案为:D
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
9.黄
【分析】根据可能性大小的判断方法,比较箱子里红球、黄球的数量,哪种颜色球的数量多,摸到的可能性就大。
【详解】3>2
黄球的数量多,所以任意摸出一个球,摸到黄球的可能性大一些。
【点睛】本题考查可能性的大小,根据事件数量的多少判断可能性的大小。
10. 红 不可能
【分析】事件发生的可能性大小是不确定的,当数量相对较多时,它发生的可能性就大;反之数量相对较少时,可能性就小。无论在什么情况下,都会发生的事件,是“一定”会发生的事件。在任何情况下,都不会发生的事件,是“不可能”事件。在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。
【详解】10>5
红球的数量比黄球的数量多,所以摸到红球的可能性大;
袋子里面没有白球,所以不可能摸到白球。
【点睛】此题主要考查事件的确定性与不确定性以及可能性的大小,明确可能性的大小与数量的多少有关是解题的关键。
11. 12 2
【分析】每个骰子六个面上分别写着数字1~6,要使两个朝上的数字相加,和最小,只需每个骰子投出的数字最小。要使两个朝上的数字相加,和最大,只需每个骰子投出的数字最大。
【详解】6+6=12
1+1=2
即和最大是12,最小是2。
【点睛】两个加数最小时,它们的和最小;两个加数最大时,它们的和最大。
12.纪念
【分析】根据题意可知,妈妈购物58元,超过50元,可参加刮奖。因为奖项中一等奖1名,二等奖3名,三等奖10名,纪念奖100名,事件发生的可能性大小是不确定的,当数量相对较多时,它发生的可能性就大;反之数量相对较少时,可能性就小。纪念奖最多,所以妈妈最有可能刮到纪念奖。
【详解】1<3<10<100
即妈妈最有可能刮中纪念奖。
【点睛】此题考查可能性的大小,刮奖活动中,数量多的奖项刮中的可能性就大,根据日常生活经验判断。
13. 黑球 白球
【分析】袋子里有几种颜色的球,从袋子里摸出球的可能性就有几种,哪种颜色球的数量越多,摸出该种颜色球的可能性就越大,哪种颜色球的数量越少,摸出该种颜色球的可能性就越小,据此解答。
【详解】分析可知,袋子里既有黑球又有白球,从袋子里任意摸出一个球,可能是黑球,也可能是白球。
【点睛】理解摸出球的可能性与袋子里球的颜色有关是解答题目的关键。
14. 黄 白
【分析】可能性的大小与球数量的多少有关,数量多则被摸到的可能性就大,反之就小。据此解答即可。
【详解】因为8>6>2
则任意摸出一个球,摸出黄球的可能性最大,摸到白球的可能性最小。
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
15.3
【分析】根据题意卡片上写着讲故事、唱歌和跳舞,小红抽一次,可能是讲故事、也可能是唱歌或跳舞。
【详解】据分析可知,小红抽一次,可能是讲故事、也可能是唱歌或跳舞,也就是可能出现3种结果。
【点睛】本题考查了可能性知识,结合题意进行分析即可。
16. 橘子 6
【分析】(1)因为果盘里有6个橙子,3个橘子,8个苹果,8>6>3,所以从果盘里任意摸出一个水果,摸到橘子的可能性最小;
(2)要想让这种水果的可能性最大,至少还要加8+1-3=6(个),据此进行填空。
【详解】果盘里有6个橙子,3个橘子,8个苹果,周星星同学随便拿出一个水果,拿到(橘子)的可能性最小,要想拿到这种水果的可能性最大,至少还要加(6)个这种水果。
【点睛】解决此题关键是根据不需要准确地计算可能性的大小时,可以根据各种水果个数的多少,直接判断可能性的大小。
17.×
【分析】无论在什么情况下,都会发生的事件,是“一定”会发生的事件。在任何情况下,都不会发生的事件,是“不可能”事件。在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。据此解答。
【详解】虽然连续四届五(5)班都是冠军,但今年五(5)班能不能得冠军并不确定,所以今年五(5)班可能是冠军,题干中的说法是错误的。
故答案为:×
【点睛】此题主要考查事件的确定性与不确定性,对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。
18.×
【分析】如果盒子里只有红珠子,任意拿一粒,拿到的一定是红珠子;如果盒子里除了红珠子还有其它颜色的珠子,任意拿一粒,可能拿到红珠子,也可能拿到其它颜色的珠子;如果盒子里没有红珠子,任意拿一粒,不可能拿到红珠子,据此解答。
【详解】由题意可知,盒子里有黄珠子和红珠子两种颜色的珠子,任意拿一粒,可能拿到黄珠子,也可能拿到红珠子。
故答案为:×
【点睛】准确地用“一定”“可能”“不可能”等词语来描述事件发生的可能性是解答题目的关键。
19.×
【分析】比较白色部分和阴影部分,哪一部分所占的区域大,指针停在哪种区域的可能性就大;如果两部分区域一样大,则指针停在两部分的可能性一样大,据此分析。
【详解】由于图中白色部分与阴影部分相等,所以转动转盘,指针停在白色部分和阴影部分的可能性相等,原题说法错误。
故答案为:×
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种颜色的区域大,发生的可能性就大一些。
20.√
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。袋子里装有1个白球和6个红球,第一次摸了白球,摸出后不放回袋子里,则余下的全部是红球,第二次一定摸到红球;据此回答。
【详解】袋子里装有一些大小相同的1个白球和6个红球,第一次摸到白球后,不放回,袋子里剩下都是红球,所以第二次一定摸到红球。原题干说法正确。
故答案为:√
【点睛】解决此类问题的关键是分两种情况:(1)需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可;(2)不需要计算可能性的大小的准确值时,可以根据各种球数量的多少,直接判断可能性的大小。
21.见详解
【分析】最大的四位数是9999。
第一个转盘内没有9,那么不可能转出最大的四位数;
第二个转盘内只有一个9,转出最大的四位数的可能性比较小;
第三个转盘内有9个9,1个0,很有可能转出最大的四位数;
第四个转盘内有3个9,可能转出最大的四位数;
第五个转盘内全部是9,一定能转出最大的四位数。
【详解】第一个转盘不可能转出最大的四位数;
第二个转盘不太可能转出最大的四位数;
第三个转盘很可能转出最大的四位数;
第四个转盘可能转出最大的四位数;
第五个转盘一定能转出最大的四位数。
连线如下:
【点睛】本题考查了可能性的大小,掌握可能性大小的判断方法是解题的关键。
22.见详解
【分析】袋子里没有白球,肯定摸不出白球;袋子里全是白球,一定摸到白球;有白球有黑球,黑球数量多,摸出黑球的可能性较大;袋子里有白球也有其它球,可能摸出白球,据此连线。
【详解】
【点睛】哪种球的数量多,发生的可能性就大一些。对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。
23.见详解
【分析】根据各种区域面积的大小,直接判断可能性的大小;如果明明赢的可能性大,则涂色区域的面积大;反之,如果华华赢的可能性大则白色区域的面积大;如果使游戏最公平,则应把两种颜色的区域涂得面积相等;据此涂色即可。
【详解】如图:
(涂法不唯一)
【点睛】本题考查可能性的大小,解决此类问题的关键是分两种情况:(1)需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答;(2)不需要计算可能性的大小的准确值时,可以根据各种区域面积的大小,直接判断可能性的大小。
24.(1)见详解;(2)见详解
【分析】(1)根据“一定摸到球”,说明这个盒子里面的球全部是球。
(2)根据“摸到球和摸到球的可能性一样大”,说明两种球一样多。
【详解】(1)一定摸到球,如图:
(2)摸到球和摸到球的可能性一样大,如图:
【点睛】正确理解“一定”、“可能”、“不可能”表示的含义,根据这个含义求解。
25.(1)(2)见详解
【分析】(1)事件发生的可能性大小是不确定的,当数量相对较多时,它发生的可能性就大;反之数量相对较少时,可能性就小。要使摸出数字“2”的可能性大,摸出数字“5”的可能性小,卡片上填数字“2”的数量比填数字“5”的数量多即可满足条件。
(2)无论在什么情况下,都会发生的事件,是“一定”会发生的事件。要使摸到的一定是数字“2”,那么卡片里数字都要填数字“2”,不能填其它的数,即可满足条件。
【详解】(1)填数如下:
或者
(2)填数如下:
【点睛】本题考查可能性的大小以及事件的确定性与不确定性,明确可能性的大小与数量的多少有关是解题的关键。
26.(1)左边
(2)右边
(3)左边
【分析】(1)盒子里全是红棋子,肯定能摸出红棋子。
(2)盒子里只要有绿棋子,且还有其它颜色的棋子,可能摸出绿棋子。
(3)盒子里没有绿棋子,不可能摸出绿棋子。
【详解】(1)左边盒子里肯定能摸出红棋子。
(2)右边盒子里可能摸出绿棋子。
(3)左边盒子里不可能摸出绿棋子。
【点睛】对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。
27.一定不可能发生
【分析】事件的确定性:“一定”表示确定事件,“可能”表示不确定事件,“不可能”属于确定事件中的必然事件,结合实际生活,按要求写出即可。
【详解】9+14=23(时)
上午9时,再过14小时,正好是23时,是深夜,一定不会有太阳出来,因此小松说的一定不可能发生。
【点睛】此题考查的是事件的确定性和不确定性,应明确事件的确定性和不确定性,并能结合实际进行正确判断。
28.聪聪;见详解
【分析】先计算出两数的和的所有情况,再看和是双数、单数分别有几种情况,哪种情况出现越多,获胜的可能性就越大。
因为数字2,5,6,8中双数多,单数少,所以要用单数替换掉其中的一张双数的卡片,让游戏更公平。
【详解】两数的和:
2+2=4, 2+5=7,2+6=8,2+8=10;
5+2=7,5+5=10,5+6=11,5+8=13;
6+2=8,6+5=11,6+6=12,6+8=14;
8+2=10,8+5=13,8+6=14,8+8=16;
一共有16种情况,和为双数的有10种情况,和为单数的有6种情况;
10>6,所以聪聪获胜的可能大。
因为单数+单数=双数,双数+双数=双数,单数+双数=单数,所以把其中一张双数卡片换成单数卡数,和出现单数和双数的可能性相等,两人获胜的可能性相等。
答:聪聪获胜的可能大。把写着数字2的卡片都换成写着数字3的卡片,这样游戏更公平。(方法不唯一)
【点睛】本题考查可能性的大小以及游戏的公平性,要使游戏公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
29.不公平;公平的游戏规则见详解
【分析】确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
【详解】小于5的数有1、2、3、4,共4种情况,等于或大于5的数有5、6、7、8、9、10,共6种情况,所以游戏规则不公平。
可以指针指向单数的得模型,指针指向双数的不得模型。(答案不唯一)
【点睛】游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。
30.不公平;点数大于5的比点数小于5的多
【分析】确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
【详解】点数大于5的有:8、9、7、6、10,共5个。
点数小于5的有:4、2、3、1,共4个。
这个游戏规则不公平,因为点数大于5的比点数小于5的多。
【点睛】游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
