人教版五年级数学上册第四单元可能性同步学案(知识点梳理+能力百分练)四
文档属性
| 名称 | 人教版五年级数学上册第四单元可能性同步学案(知识点梳理+能力百分练)四 |

|
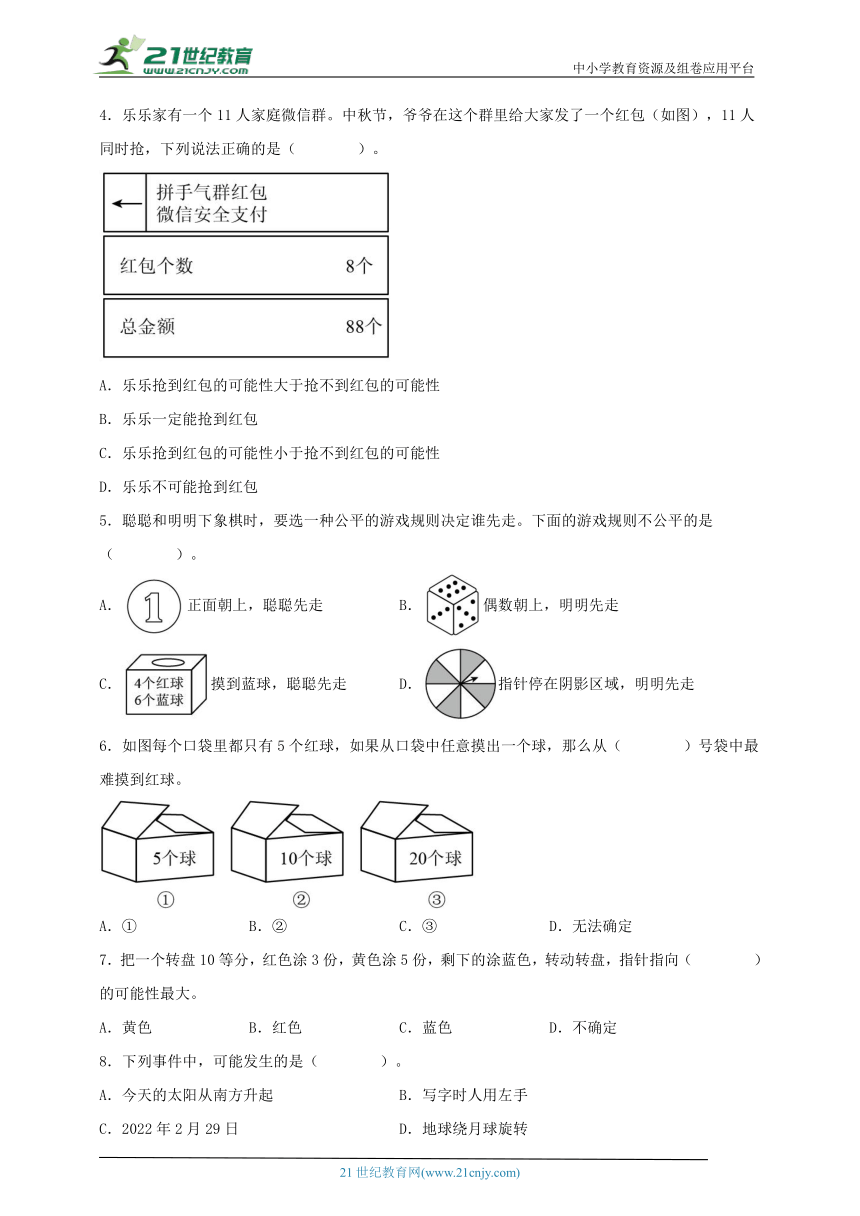
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 06:26:20 | ||
图片预览

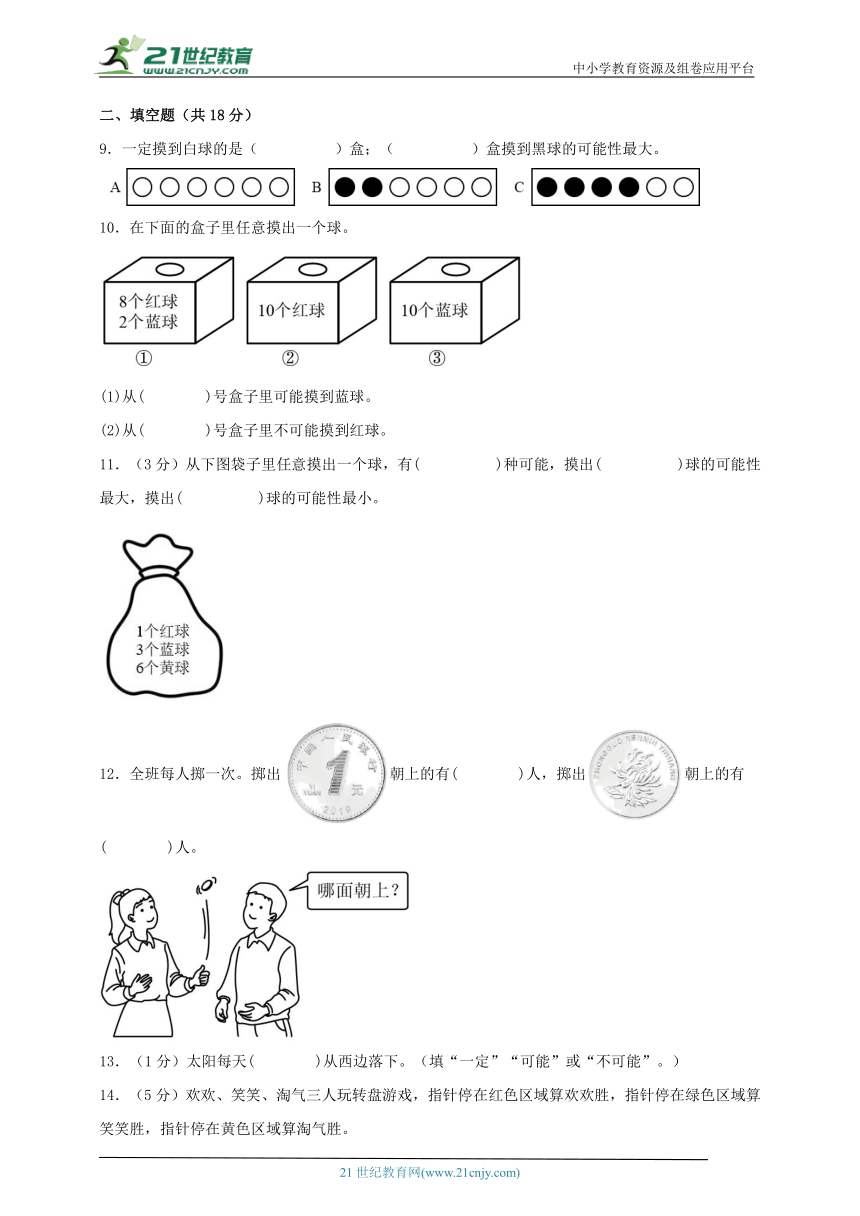

文档简介
中小学教育资源及组卷应用平台
人教版五年级数学上册第四单元可能性(知识点梳理+能力百分练)四
知识点梳理
1、事件发生有确定性和不确定性,确定事件也就是一定会发生的或一定不会发生的事件,用“一定”、“不可能”来描述,不确定事件用“可能”来描述。
2、在游戏中,我们可以发现事件发生的可能性不同主要是受到了大小,数量,面积等原因,总结来说也就是某种情况在总数中所占比重越多,某一事件发生的可能性就越大。
3、设计与可能性相关的游戏时,先要知道游戏的所有可能性,再根据要求修改各种不同的事件发生的可能性。
能力百分练
一、选择题(共16分)
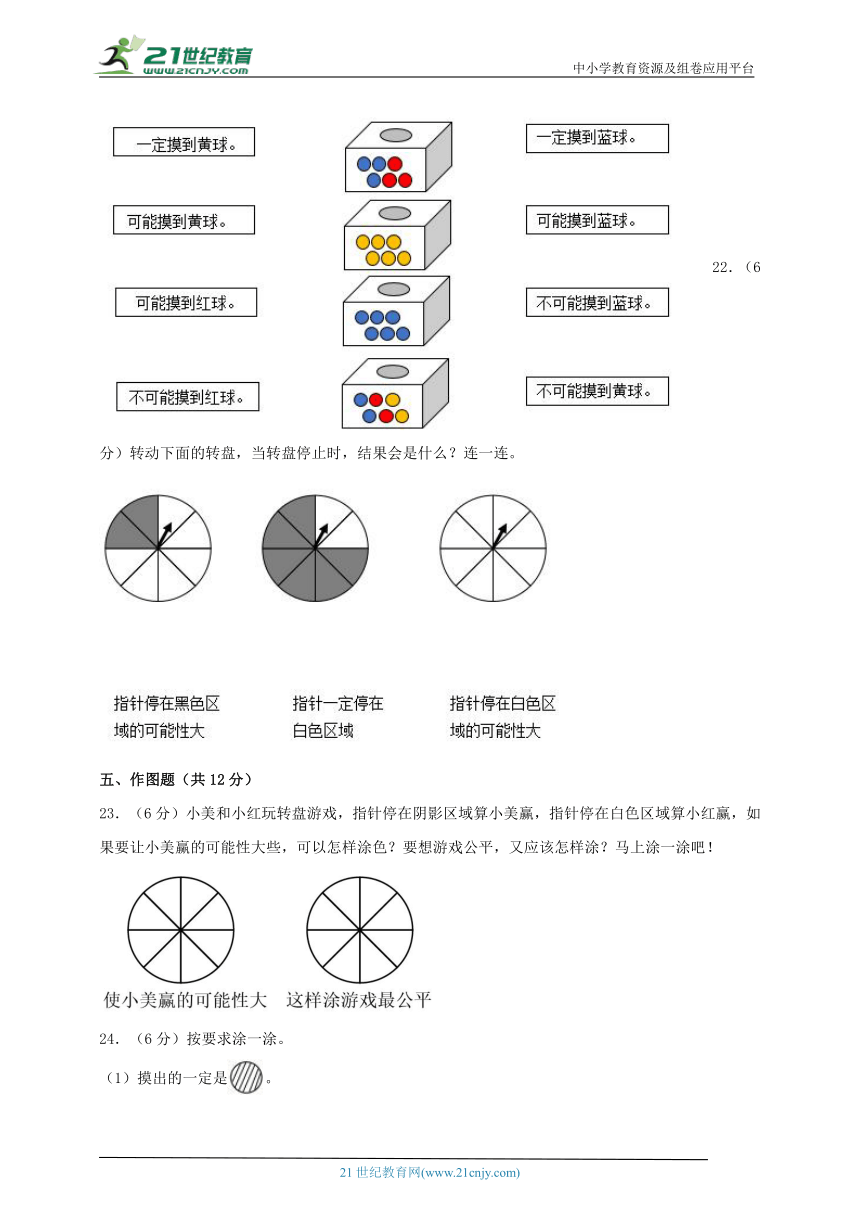
1.在装有红球、黄球、白球的袋子里,( )摸出绿球。
A.可能 B.一定能 C.不可能 D.不确定
2.盒子里装有黑、白两种颜色的球,丁丁从中摸出一个球后再放回去摇匀,重复20次并记录下球的颜色,情况如图。如果丁丁再摸一次,下面哪句话的描述是正确的?( )
● 正正正
○
A.一定摸到黑球
B.一定摸到白球
C.摸到黑球的可能性比较大
D.摸到白球的可能性比较大
3.把下面四张扑克牌反扣在桌面上,并把它们的次序打乱,任意摸一张。下面说法错误的是( )。
A.摸到9的可能性最大
B.摸到9的可能性比7大
C.摸到7和10的可能性一样大
D.摸到7、9和10的可能性一样大
4.乐乐家有一个11人家庭微信群。中秋节,爷爷在这个群里给大家发了一个红包(如图),11人同时抢,下列说法正确的是( )。
A.乐乐抢到红包的可能性大于抢不到红包的可能性
B.乐乐一定能抢到红包
C.乐乐抢到红包的可能性小于抢不到红包的可能性
D.乐乐不可能抢到红包
5.聪聪和明明下象棋时,要选一种公平的游戏规则决定谁先走。下面的游戏规则不公平的是( )。
A.正面朝上,聪聪先走 B.偶数朝上,明明先走
C.摸到蓝球,聪聪先走 D.指针停在阴影区域,明明先走
6.如图每个口袋里都只有5个红球,如果从口袋中任意摸出一个球,那么从( )号袋中最难摸到红球。
A.① B.② C.③ D.无法确定
7.把一个转盘10等分,红色涂3份,黄色涂5份,剩下的涂蓝色,转动转盘,指针指向( )的可能性最大。
A.黄色 B.红色 C.蓝色 D.不确定
8.下列事件中,可能发生的是( )。
A.今天的太阳从南方升起 B.写字时人用左手
C.2022年2月29日 D.地球绕月球旋转
二、填空题(共18分)
9.一定摸到白球的是( )盒;( )盒摸到黑球的可能性最大。
10.在下面的盒子里任意摸出一个球。
(1)从( )号盒子里可能摸到蓝球。
(2)从( )号盒子里不可能摸到红球。
11.(3分)从下图袋子里任意摸出一个球,有( )种可能,摸出( )球的可能性最大,摸出( )球的可能性最小。
12.全班每人掷一次。掷出朝上的有( )人,掷出朝上的有( )人。
13.(1分)太阳每天( )从西边落下。(填“一定”“可能”或“不可能”。)
14.(5分)欢欢、笑笑、淘气三人玩转盘游戏,指针停在红色区域算欢欢胜,指针停在绿色区域算笑笑胜,指针停在黄色区域算淘气胜。
(1)淘气想让自己胜的可能性最大,应选( )号转盘。
(2)用( )号转盘做游戏,对他们三人都公平。
(3)选②号转盘,( )胜的可能性最大。
(4)选( )号转盘,欢欢、笑笑和淘气三人输的可能性一样大。
(5)他们三个玩了30次,每人胜的次数如下表,根据表中的数据,他们可能用的是( )号转盘。
欢欢 笑笑 淘气
8 14 8
15.(1分)元旦到了,五(1)班举行文艺活动,准备了10个签,其中6个签为舞蹈类节目,4个签为语言类节目,陈芳同学从中抽出一个签,抽到( )类节目的可能性大。
16.给涂上红、蓝两种颜色,要使掷出蓝色朝上的可能性比红色大,红色可以涂( )面,蓝色可以涂( )面。
三、判断题(共8分)
17.生活中用“石头、剪刀、布”决定输赢的方法是公平的。( )
18.转动如图的转盘,指针停在白色部分的可能性大。( )
19.从一副完整的扑克牌中抽出一张牌,抽到大王的可能性和抽到小王的可能性一样大。( )
20.在一次彩票有奖销售活动中,李叔叔买了100张彩票,一定能中奖。( )
四、连线题(共12分)
21.(6分)从盒子里摸出一个球,结果会是什么?连一连。
22.(6分)转动下面的转盘,当转盘停止时,结果会是什么?连一连。
五、作图题(共12分)
23.(6分)小美和小红玩转盘游戏,指针停在阴影区域算小美赢,指针停在白色区域算小红赢,如果要让小美赢的可能性大些,可以怎样涂色?要想游戏公平,又应该怎样涂?马上涂一涂吧!
24.(6分)按要求涂一涂。
(1)摸出的一定是。
(2)摸出和的可能性一样大。
六、解答题(共34分)
25.(6分)在下面的每个转盘中,指针停在哪种颜色区域的可能性最大?停在哪种颜色区域的可能性最小?
26.(6分)转动指针,说一说指针可能停在哪种颜色的区域上。
27.(8分)口袋里有8个黄球和2个红球。
(1)一次摸出一个球,可能有哪些结果?
(2)请你预测一下,摸出什么球的可能性最大?摸出什么球的可能性最小?
28.(6分)现有12个小球要放入盒子中,随意摸出一个,要使摸出红球的可能性是摸出黑球可能性的3倍,那红球、黑球各有几个?请你涂一涂或用文字表示颜色。
29.(8分)请你利用下面的圆形设计一个抽奖转盘的模拟图,使指针停在一等奖、二等奖、三等奖区域的可能性关系是:若一等奖1名,则二等奖3名、三等奖4名。
(1)请你完成抽奖转盘的模拟图。
(2)获几等奖的可能性最大?写出你的想法。
参考答案
1.C
【分析】根据题意,在装有红球、黄球、白球的袋子里,没有绿球,所以不可能摸出绿球。
【详解】在装有红球、黄球、白球的袋子里,不可能摸出绿球。
故答案为:C
【点睛】本题考查可能性的知识,判断事件发生的可能性的几种情况:可能、不可能、一定;在任何情况下,都不会发生的事件,是“不可能”事件。
2.C
【分析】根据判断事件发生的可能性,因为盒子里装有黑、白两种颜色的球,如果丁丁再摸一次,可能摸到黑球,也可能摸到白球。
根据可能性大小的判断方法,比较黑球、白球摸到的次数,次数多的,摸到的可能性就大;反之,次数少的,摸到的可能性就小。
【详解】A.如果丁丁再摸一次,可能摸到黑球,原题说法错误;
B.如果丁丁再摸一次,可能摸到白球,原题说法错误;
C.18>2,如果丁丁再摸一次,摸到黑球的可能性比较大,原题说法正确;
D.2<18,如果丁丁再摸一次,摸到白球的可能性比较小,原题说法错误。
故答案为:C
【点睛】本题考查可能性的知识,注意每一次摸球都是独立的随机试验,不能根据概率确定下一次一定摸到哪种颜色的球。
3.D
【分析】从图中可知,9有2张,7有1张,10有1张;根据可能性大小的判断方法,数量最多的,摸到的可能性最大;反之,数量最少的,摸到的可能性就最小;数量相等的,摸到的可能性一样大。
【详解】A.9的张数最多,所以摸到9的可能性最大,原题说法正确;
B.9的张数比7的张数多,所以摸到9的可能性比7大,原题说法正确;
C.7和10的张数一样多,所以摸到7和10的可能性一样大,原题说法正确;
D.7、9、10的张数不一样多,所以摸到7、9和10的可能性不一样大,原题说法错误。
故答案为:D
【点睛】本题考查可能性的大小,根据事件数量的多少判断可能性的大小。
4.A
【分析】要想抢到红包的可能性差不多,则红包和群里的人数要差不多,红包的数量一定,群里的人数越多,抢到的可能性越小,据此解答即可。
【详解】11-8=3(人)
11人抢8个红包,则有3人抢不到红包;
8>3
则乐乐抢到红包的可能性大于抢不到红包的可能性。
故答案为:A
【点睛】本题主要考查了可能性的问题,数量越多可能性越大。
5.C
【分析】只要两人先走的可能性相等,游戏就是公平的,否则就是不公平的。
【详解】A.硬币只有正面和反面,所以出现正面和反面的可能性相同,游戏规则公平;
B.骰子共有6个面,分别是1、2、3、4、5、6,其中偶数和奇数各有3个,所以出现偶数和奇数的可能性相同,游戏规则公平;
C.红球有4个,蓝球有6个,则摸到蓝球的可能性大一些,游戏规则不公平;
D.阴影部分和空白部分的面积相同,所以指针停在阴影区域和空白区域的可能性相同,游戏规则公平。
故答案为:C
【点睛】本题主要考查学生对可能性的大小知识的掌握和灵活运用。
6.C
【分析】红球在每个口袋里的数量越多,则摸到的可能性越大,反之,则摸到的可能性越小。
【详解】①中5个球都是红球,一定摸到红球;
②中有10个球,5个是红球,占一半;
③中有20个球,5个是红球,占据的数量较少,所以最难摸到红球。
则从③号口袋中最难摸到红球。
故答案为:C
【点睛】本题考查可能性的大小,解答本题的关键是掌握可能性的概念。
7.A
【分析】由题可知,把一个转盘10等分,红色涂3份,黄色涂5份,蓝色则占10-3-5=2份,然后根据数量多的可能性就大来解答即可。
【详解】蓝色:10-3-5
=7-5
=2
2<3<5
所以指针指向黄色的可能性最大。
故答案为:A
【点睛】解决此题关键是根据不需要准确地计算可能性的大小时,可以根据所占份数的多少,直接判断可能性的大小。
8.B
【分析】事件发生的可能性的大小,对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。无论在什么情况下,都会发生的事件,是“一定”会发生的事件;在任何情况下,都不会发生的事件,是“不可能”事件;在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。
【详解】根据生活实际可知,
A.今天的太阳从南方升起是不可能,不符合题意;
B.写字时,人可能用左手,符合题意;
C.2022÷4=505……2,所以2022年是平年,2月有28天,所以此项说法错误;
D.地球绕月球旋转,是不符合实际的,不符合题意。
故答案为:B
【点睛】联系生活实际,正确判定事件的确定性与不确定性,是解答此题的关键。
9. A C
【分析】根据可能性大小的判断方法,盒子里哪种颜色球的数量多,摸到的可能性就大;哪种颜色球的数量少,摸到的可能性就小;盒子如果只有一种颜色的球,那么一定可以摸到这种颜色的球。
【详解】A盒子里只有白球,所以一定摸到白球;
B盒子里有2个黑球,4个白球,2<4,摸到黑球的可能性小;
C盒子里有4个黑球,2个白球,4>2,摸到黑球的可能性大;
所以,一定摸到白球的是A盒;C盒摸到黑球的可能性最大。
【点睛】本题考查可能性的大小,根据黑球和白球数量的多少判断事件发生可能性的大小是解答题目的关键。
10.(1)①
(2)③
【分析】如果盒子里既有蓝球,也有其它颜色的球,那么从盒子里任意摸出一个球可能是蓝球;如果盒子里没有红球,那么从盒子里任意摸出一个球不可能是红球,据此解答。
【详解】(1)①号盒子里有红球和蓝球两种颜色的球,从盒子里任意摸出一个球,可能摸到蓝球,也可能摸到红球。
(2)③号盒子里只有蓝球,从盒子里任意摸出一个球,一定是蓝球,不可能是红球。
【点睛】根据盒子里球的颜色判断事件发生的确定与不确定性是解答题目的关键。
11. 3/三 黄 红
【分析】根据题意,袋子里有红球、蓝球、黄球三种颜色的球,那么任意摸出一个球,就有可能摸到这三种颜色的球中的任何一个,所以有3种可能的结果。
根据可能性大小的判断方法,比较袋子里红球、蓝球、黄球的数量多少,数量最多的,摸到的可能性最大;数量最少的,摸到的可能性最小。
【详解】6>3>1
黄球最多,红球最少;
从袋子里任意摸出一个球,有3种可能,摸出黄球的可能性最大,摸出红球的可能性最小。
【点睛】本题考查可能性的知识,根据事件数量的多少判断可能性的大小。
12. 23 22
【分析】根据班级人数和操作情况进行填空,抛出正面朝上和反面朝上的可能性一样大,一般情况,抛的次数越多,正面和反面朝上的人数越接近。
【详解】如果全班有45人,全班每人掷一次。掷出朝上的可能有23人,掷出朝上的可能有22人。(答案不唯一)
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。正面和反面一样多,发生的可能性一样大。
13.一定
【分析】太阳东升西落属于客观规律,属于确定事件中的必然事件;太阳一定会从西边落下。
【详解】由分析可知:
太阳每天一定从西边落下。
【点睛】此题应根据事件的确定性和不确定性进行分析、解答,正确使用“一定”、“可能”、“不可能”这三个词语。
14.(1)④
(2)①
(3)欢欢
(4)①
(5)③
【分析】(1)指针停在黄色区域算淘气胜,哪个转盘黄色区域最大,淘气胜的可能性就最大。
(2)红黄绿三种颜色的区域一样大,三个人胜的可能性一样大,就对他们三人都公平。
(3)②号转盘红色区域大,指针指向红色区域的可能性大,指针停在红色区域算欢欢胜。
(4)三个人胜的可能性一样大,则输的可能性就一样大。
(5)谁胜的次数多,说明谁对应颜色的区域大,根据胜的次数逆推出转盘即可。
【详解】(1)淘气想让自己胜的可能性最大,应选④号转盘。
(2)用①号转盘做游戏,对他们三人都公平。
(3)选②号转盘,欢欢胜的可能性最大。
(4)选①号转盘,欢欢、笑笑和淘气三人输的可能性一样大。
(5)他们可能用的是③号转盘。
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种颜色的区域大,发生的可能性就大一些。
15.舞蹈
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。舞蹈类节目的签数量大于语言类节目的签数量,则抽到舞蹈类节目的可能性大。
【详解】6>4
陈芳同学从中抽出一个签,抽到舞蹈类节目的可能性大。
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
16. 1 5
【分析】要使掷出蓝色朝上的可能性比红色大,蓝色的面要比红色的面多,据此解答即可。
【详解】由分析可得:要使掷出蓝色朝上的可能性比红色大,红色涂1个面,蓝色涂5个面。(答案不唯一)
【点睛】根据可能性的大小,直接判断涂色面的多少,据此解答即可。
17.√
【分析】游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
【详解】有可能出“石头、剪刀、布”中的任何一个,三种结果赢的可能性相等。
所以,生活中用“石头、剪刀、布”决定输赢的方法是公平的。
原题说法正确;
故答案为:√
【点睛】本题考查游戏的公平性,明确要使游戏公平,发生的可能性必须相等。
18.×
【分析】比较白色部分和阴影部分,哪一部分所占的区域大,指针停在哪种区域的可能性就大;如果两部分区域一样大,则指针停在两部分的可能性一样大,据此分析。
【详解】由于图中白色部分与阴影部分相等,所以转动转盘,指针停在白色部分和阴影部分的可能性相等,原题说法错误。
故答案为:×
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种颜色的区域大,发生的可能性就大一些。
19.√
【分析】哪种牌面的数量越多,抽到的可能性就越大;两种牌面的数量同样多,抽到的可能性就一样大,据此分析。
【详解】一副完整的扑克牌有一个大王和一个小王,大王和小王的数量同样多,抽到大王的可能性和抽到小王的可能性一样大,原题说法正确。
故答案为:√
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种牌的数量多,发生的可能性就大一些。
20.×
【分析】确定事件包括必然事件和不可能事件:必然事件指在一定条件下,一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件,即随机事件是指在一定条件下,可能发生也可能不发生的事件。李叔叔买彩票中不中奖,属于不确定事件,有可能发生,也有可能不发生,据此解答即可。
【详解】李叔叔买了100张彩票,他有可能中奖,也有可能不中奖。原说法错误。
故答案为:×
【点睛】本题主要考查确定事件、不确定事件的定义。
21.见详解
【分析】盒子里全是黄球,摸到的一定是黄球;盒子里只要有黄球,就可能摸到黄球;盒子里只要有红球,就可能摸到红球;盒子里没有红球,不可能摸到红球;盒子里全是蓝求,一定摸到蓝球;盒子里只要有蓝球,就可能摸到蓝球;盒子里没有蓝球,不可能摸到蓝球;盒子里没有黄球,不可能摸到黄球,据此连线。
【详解】
【点睛】对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。
22.图见详解
【分析】图一白色区域面积远大于深色区域面积,所以指针很可能落在白色区域;
图二深色区域面积远大于白色区域,所以指针落在深色区域的可能性很大;
图三只有白色区域,所以指针一定停在白色区域,据此连线。
【详解】作图如下:
【点睛】本题考查了可能性,转盘上哪种颜色的区域面积大,指针落在该区域的可能性就大。
23.见详解
【分析】根据可能性大小的判断方法,想让小美赢的可能性大些,那么涂阴影区域要比白色区域多;
想让游戏公平,那么涂阴影区域和白色区域一样多,这样两人赢的可能性一样大。
【详解】如图:
(答案不唯一)
【点睛】本题考查可能性的大小,根据事件数量的多少判断可能性的大小。
24.见详解
【分析】(1)根据题意,摸出的一定是,要使事件一定发生,那么就要排除其他情况,只剩一种情况,也就是箱子里面就只有;
(2)摸出和的可能性一样大,也就是和的数量同样多即可。
【详解】(1)涂色如下:
(2)涂色如下:(涂法不唯一,两种颜色数量相等即可)
【点睛】此题考查了可能性的知识,关键能够结合数量情况改变可能性的大小。
25.第一个转盘:蓝色区域可能性最大,黄色区域可能性最小;第二个转盘:红色区域可能性最大,蓝色区域可能性最小
【分析】转盘上哪种颜色的区域最大,指针停在哪种颜色区域的可能性最大;哪种颜色的区域最小,指针停在哪种颜色区域的可能性最小。
【详解】第一个转盘,因为蓝色区域最大,所以指针停在蓝色区域的可能性最大,黄色区域最小,所以指针停在黄色区域的可能性最小;
第二个转盘,因为红色区域最大,所以指针停在红色区域的可能性最大,蓝色区域最小,所以指针停在蓝色区域的可能性最小。
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种颜色的区域大,发生的可能性就大一些。
26.蓝色、粉色、绿色或黄色
【分析】可能性的大小与区域的面积的大小有关,哪种颜色的区域的面积大,则停在该区域的可能性就大,反之就小;若每种颜色的区域的面积一样大,则停在这几种颜色区域的可能性一样大。
【详解】因为蓝色、粉色、绿色和黄色区域的面积一样大,则指针停在这四种区域的可能性一样大。
答:指针可能停在蓝色、粉色、绿色或黄色的区域上。
【点睛】本题考查可能性,明确可能性的大小与区域的面积的大小有关是解题的关键。
27.(1)可能摸出黄球,也可能摸出红球;(2)摸出黄球的可能性最大;摸出红球的可能性最小
【分析】(1)口袋里只有黄球和红球,一次摸出一个球,所以只可能摸出黄球或红球;
(2)不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。黄球的个数大于红球的个数,所以摸出黄球的可能性大于红球的可能性。
【详解】(1)一次摸出一个球,可能摸出黄球也可能摸出红球。
(2)8>2
黄球的个数大于红球的个数,
所以摸出黄球的可能性最大,摸出红球的可能性最小。
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
28.红球有9个,黑球有3个,图见详解
【分析】根据题意,要使摸出红球的可能性是摸出黑球可能性的3倍,如果红球有3,那么黑球有1,利用12除以(3+1)即可求出黑球的数量,再乘3即可求出红球的数量,再涂色即可。
【详解】12÷(3+1)
=12÷4
=3(个)
3×3=9(个)
如图:
【点睛】本题主要考查可能性的求法。
29.(1)见详解
(2)三等奖;三等奖占4份,占的份数最多,转动转盘时,指针停在三等奖区域的可能性最大,因此获三等奖的可能性最大。
【分析】(1)三等奖占4份,占的份数最多,转动转盘时,指针停在三等奖区域的可能性最大,据此作图即可。
(2)可能性的大小与所占区域的大小有关,区域越大则可能性越大,反之则小,据此解答。
【详解】(1)由分析可知,作图如下:
(2)三等奖;三等奖占4份,占的份数最多,转动转盘时,指针停在三等奖区域的可能性最大,因此获三等奖的可能性最大。
【点睛】本题考查可能性的大小,明确所占区域越大则可能性越大,反之则小是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版五年级数学上册第四单元可能性(知识点梳理+能力百分练)四
知识点梳理
1、事件发生有确定性和不确定性,确定事件也就是一定会发生的或一定不会发生的事件,用“一定”、“不可能”来描述,不确定事件用“可能”来描述。
2、在游戏中,我们可以发现事件发生的可能性不同主要是受到了大小,数量,面积等原因,总结来说也就是某种情况在总数中所占比重越多,某一事件发生的可能性就越大。
3、设计与可能性相关的游戏时,先要知道游戏的所有可能性,再根据要求修改各种不同的事件发生的可能性。
能力百分练
一、选择题(共16分)
1.在装有红球、黄球、白球的袋子里,( )摸出绿球。
A.可能 B.一定能 C.不可能 D.不确定
2.盒子里装有黑、白两种颜色的球,丁丁从中摸出一个球后再放回去摇匀,重复20次并记录下球的颜色,情况如图。如果丁丁再摸一次,下面哪句话的描述是正确的?( )
● 正正正
○
A.一定摸到黑球
B.一定摸到白球
C.摸到黑球的可能性比较大
D.摸到白球的可能性比较大
3.把下面四张扑克牌反扣在桌面上,并把它们的次序打乱,任意摸一张。下面说法错误的是( )。
A.摸到9的可能性最大
B.摸到9的可能性比7大
C.摸到7和10的可能性一样大
D.摸到7、9和10的可能性一样大
4.乐乐家有一个11人家庭微信群。中秋节,爷爷在这个群里给大家发了一个红包(如图),11人同时抢,下列说法正确的是( )。
A.乐乐抢到红包的可能性大于抢不到红包的可能性
B.乐乐一定能抢到红包
C.乐乐抢到红包的可能性小于抢不到红包的可能性
D.乐乐不可能抢到红包
5.聪聪和明明下象棋时,要选一种公平的游戏规则决定谁先走。下面的游戏规则不公平的是( )。
A.正面朝上,聪聪先走 B.偶数朝上,明明先走
C.摸到蓝球,聪聪先走 D.指针停在阴影区域,明明先走
6.如图每个口袋里都只有5个红球,如果从口袋中任意摸出一个球,那么从( )号袋中最难摸到红球。
A.① B.② C.③ D.无法确定
7.把一个转盘10等分,红色涂3份,黄色涂5份,剩下的涂蓝色,转动转盘,指针指向( )的可能性最大。
A.黄色 B.红色 C.蓝色 D.不确定
8.下列事件中,可能发生的是( )。
A.今天的太阳从南方升起 B.写字时人用左手
C.2022年2月29日 D.地球绕月球旋转
二、填空题(共18分)
9.一定摸到白球的是( )盒;( )盒摸到黑球的可能性最大。
10.在下面的盒子里任意摸出一个球。
(1)从( )号盒子里可能摸到蓝球。
(2)从( )号盒子里不可能摸到红球。
11.(3分)从下图袋子里任意摸出一个球,有( )种可能,摸出( )球的可能性最大,摸出( )球的可能性最小。
12.全班每人掷一次。掷出朝上的有( )人,掷出朝上的有( )人。
13.(1分)太阳每天( )从西边落下。(填“一定”“可能”或“不可能”。)
14.(5分)欢欢、笑笑、淘气三人玩转盘游戏,指针停在红色区域算欢欢胜,指针停在绿色区域算笑笑胜,指针停在黄色区域算淘气胜。
(1)淘气想让自己胜的可能性最大,应选( )号转盘。
(2)用( )号转盘做游戏,对他们三人都公平。
(3)选②号转盘,( )胜的可能性最大。
(4)选( )号转盘,欢欢、笑笑和淘气三人输的可能性一样大。
(5)他们三个玩了30次,每人胜的次数如下表,根据表中的数据,他们可能用的是( )号转盘。
欢欢 笑笑 淘气
8 14 8
15.(1分)元旦到了,五(1)班举行文艺活动,准备了10个签,其中6个签为舞蹈类节目,4个签为语言类节目,陈芳同学从中抽出一个签,抽到( )类节目的可能性大。
16.给涂上红、蓝两种颜色,要使掷出蓝色朝上的可能性比红色大,红色可以涂( )面,蓝色可以涂( )面。
三、判断题(共8分)
17.生活中用“石头、剪刀、布”决定输赢的方法是公平的。( )
18.转动如图的转盘,指针停在白色部分的可能性大。( )
19.从一副完整的扑克牌中抽出一张牌,抽到大王的可能性和抽到小王的可能性一样大。( )
20.在一次彩票有奖销售活动中,李叔叔买了100张彩票,一定能中奖。( )
四、连线题(共12分)
21.(6分)从盒子里摸出一个球,结果会是什么?连一连。
22.(6分)转动下面的转盘,当转盘停止时,结果会是什么?连一连。
五、作图题(共12分)
23.(6分)小美和小红玩转盘游戏,指针停在阴影区域算小美赢,指针停在白色区域算小红赢,如果要让小美赢的可能性大些,可以怎样涂色?要想游戏公平,又应该怎样涂?马上涂一涂吧!
24.(6分)按要求涂一涂。
(1)摸出的一定是。
(2)摸出和的可能性一样大。
六、解答题(共34分)
25.(6分)在下面的每个转盘中,指针停在哪种颜色区域的可能性最大?停在哪种颜色区域的可能性最小?
26.(6分)转动指针,说一说指针可能停在哪种颜色的区域上。
27.(8分)口袋里有8个黄球和2个红球。
(1)一次摸出一个球,可能有哪些结果?
(2)请你预测一下,摸出什么球的可能性最大?摸出什么球的可能性最小?
28.(6分)现有12个小球要放入盒子中,随意摸出一个,要使摸出红球的可能性是摸出黑球可能性的3倍,那红球、黑球各有几个?请你涂一涂或用文字表示颜色。
29.(8分)请你利用下面的圆形设计一个抽奖转盘的模拟图,使指针停在一等奖、二等奖、三等奖区域的可能性关系是:若一等奖1名,则二等奖3名、三等奖4名。
(1)请你完成抽奖转盘的模拟图。
(2)获几等奖的可能性最大?写出你的想法。
参考答案
1.C
【分析】根据题意,在装有红球、黄球、白球的袋子里,没有绿球,所以不可能摸出绿球。
【详解】在装有红球、黄球、白球的袋子里,不可能摸出绿球。
故答案为:C
【点睛】本题考查可能性的知识,判断事件发生的可能性的几种情况:可能、不可能、一定;在任何情况下,都不会发生的事件,是“不可能”事件。
2.C
【分析】根据判断事件发生的可能性,因为盒子里装有黑、白两种颜色的球,如果丁丁再摸一次,可能摸到黑球,也可能摸到白球。
根据可能性大小的判断方法,比较黑球、白球摸到的次数,次数多的,摸到的可能性就大;反之,次数少的,摸到的可能性就小。
【详解】A.如果丁丁再摸一次,可能摸到黑球,原题说法错误;
B.如果丁丁再摸一次,可能摸到白球,原题说法错误;
C.18>2,如果丁丁再摸一次,摸到黑球的可能性比较大,原题说法正确;
D.2<18,如果丁丁再摸一次,摸到白球的可能性比较小,原题说法错误。
故答案为:C
【点睛】本题考查可能性的知识,注意每一次摸球都是独立的随机试验,不能根据概率确定下一次一定摸到哪种颜色的球。
3.D
【分析】从图中可知,9有2张,7有1张,10有1张;根据可能性大小的判断方法,数量最多的,摸到的可能性最大;反之,数量最少的,摸到的可能性就最小;数量相等的,摸到的可能性一样大。
【详解】A.9的张数最多,所以摸到9的可能性最大,原题说法正确;
B.9的张数比7的张数多,所以摸到9的可能性比7大,原题说法正确;
C.7和10的张数一样多,所以摸到7和10的可能性一样大,原题说法正确;
D.7、9、10的张数不一样多,所以摸到7、9和10的可能性不一样大,原题说法错误。
故答案为:D
【点睛】本题考查可能性的大小,根据事件数量的多少判断可能性的大小。
4.A
【分析】要想抢到红包的可能性差不多,则红包和群里的人数要差不多,红包的数量一定,群里的人数越多,抢到的可能性越小,据此解答即可。
【详解】11-8=3(人)
11人抢8个红包,则有3人抢不到红包;
8>3
则乐乐抢到红包的可能性大于抢不到红包的可能性。
故答案为:A
【点睛】本题主要考查了可能性的问题,数量越多可能性越大。
5.C
【分析】只要两人先走的可能性相等,游戏就是公平的,否则就是不公平的。
【详解】A.硬币只有正面和反面,所以出现正面和反面的可能性相同,游戏规则公平;
B.骰子共有6个面,分别是1、2、3、4、5、6,其中偶数和奇数各有3个,所以出现偶数和奇数的可能性相同,游戏规则公平;
C.红球有4个,蓝球有6个,则摸到蓝球的可能性大一些,游戏规则不公平;
D.阴影部分和空白部分的面积相同,所以指针停在阴影区域和空白区域的可能性相同,游戏规则公平。
故答案为:C
【点睛】本题主要考查学生对可能性的大小知识的掌握和灵活运用。
6.C
【分析】红球在每个口袋里的数量越多,则摸到的可能性越大,反之,则摸到的可能性越小。
【详解】①中5个球都是红球,一定摸到红球;
②中有10个球,5个是红球,占一半;
③中有20个球,5个是红球,占据的数量较少,所以最难摸到红球。
则从③号口袋中最难摸到红球。
故答案为:C
【点睛】本题考查可能性的大小,解答本题的关键是掌握可能性的概念。
7.A
【分析】由题可知,把一个转盘10等分,红色涂3份,黄色涂5份,蓝色则占10-3-5=2份,然后根据数量多的可能性就大来解答即可。
【详解】蓝色:10-3-5
=7-5
=2
2<3<5
所以指针指向黄色的可能性最大。
故答案为:A
【点睛】解决此题关键是根据不需要准确地计算可能性的大小时,可以根据所占份数的多少,直接判断可能性的大小。
8.B
【分析】事件发生的可能性的大小,对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。无论在什么情况下,都会发生的事件,是“一定”会发生的事件;在任何情况下,都不会发生的事件,是“不可能”事件;在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。
【详解】根据生活实际可知,
A.今天的太阳从南方升起是不可能,不符合题意;
B.写字时,人可能用左手,符合题意;
C.2022÷4=505……2,所以2022年是平年,2月有28天,所以此项说法错误;
D.地球绕月球旋转,是不符合实际的,不符合题意。
故答案为:B
【点睛】联系生活实际,正确判定事件的确定性与不确定性,是解答此题的关键。
9. A C
【分析】根据可能性大小的判断方法,盒子里哪种颜色球的数量多,摸到的可能性就大;哪种颜色球的数量少,摸到的可能性就小;盒子如果只有一种颜色的球,那么一定可以摸到这种颜色的球。
【详解】A盒子里只有白球,所以一定摸到白球;
B盒子里有2个黑球,4个白球,2<4,摸到黑球的可能性小;
C盒子里有4个黑球,2个白球,4>2,摸到黑球的可能性大;
所以,一定摸到白球的是A盒;C盒摸到黑球的可能性最大。
【点睛】本题考查可能性的大小,根据黑球和白球数量的多少判断事件发生可能性的大小是解答题目的关键。
10.(1)①
(2)③
【分析】如果盒子里既有蓝球,也有其它颜色的球,那么从盒子里任意摸出一个球可能是蓝球;如果盒子里没有红球,那么从盒子里任意摸出一个球不可能是红球,据此解答。
【详解】(1)①号盒子里有红球和蓝球两种颜色的球,从盒子里任意摸出一个球,可能摸到蓝球,也可能摸到红球。
(2)③号盒子里只有蓝球,从盒子里任意摸出一个球,一定是蓝球,不可能是红球。
【点睛】根据盒子里球的颜色判断事件发生的确定与不确定性是解答题目的关键。
11. 3/三 黄 红
【分析】根据题意,袋子里有红球、蓝球、黄球三种颜色的球,那么任意摸出一个球,就有可能摸到这三种颜色的球中的任何一个,所以有3种可能的结果。
根据可能性大小的判断方法,比较袋子里红球、蓝球、黄球的数量多少,数量最多的,摸到的可能性最大;数量最少的,摸到的可能性最小。
【详解】6>3>1
黄球最多,红球最少;
从袋子里任意摸出一个球,有3种可能,摸出黄球的可能性最大,摸出红球的可能性最小。
【点睛】本题考查可能性的知识,根据事件数量的多少判断可能性的大小。
12. 23 22
【分析】根据班级人数和操作情况进行填空,抛出正面朝上和反面朝上的可能性一样大,一般情况,抛的次数越多,正面和反面朝上的人数越接近。
【详解】如果全班有45人,全班每人掷一次。掷出朝上的可能有23人,掷出朝上的可能有22人。(答案不唯一)
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。正面和反面一样多,发生的可能性一样大。
13.一定
【分析】太阳东升西落属于客观规律,属于确定事件中的必然事件;太阳一定会从西边落下。
【详解】由分析可知:
太阳每天一定从西边落下。
【点睛】此题应根据事件的确定性和不确定性进行分析、解答,正确使用“一定”、“可能”、“不可能”这三个词语。
14.(1)④
(2)①
(3)欢欢
(4)①
(5)③
【分析】(1)指针停在黄色区域算淘气胜,哪个转盘黄色区域最大,淘气胜的可能性就最大。
(2)红黄绿三种颜色的区域一样大,三个人胜的可能性一样大,就对他们三人都公平。
(3)②号转盘红色区域大,指针指向红色区域的可能性大,指针停在红色区域算欢欢胜。
(4)三个人胜的可能性一样大,则输的可能性就一样大。
(5)谁胜的次数多,说明谁对应颜色的区域大,根据胜的次数逆推出转盘即可。
【详解】(1)淘气想让自己胜的可能性最大,应选④号转盘。
(2)用①号转盘做游戏,对他们三人都公平。
(3)选②号转盘,欢欢胜的可能性最大。
(4)选①号转盘,欢欢、笑笑和淘气三人输的可能性一样大。
(5)他们可能用的是③号转盘。
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种颜色的区域大,发生的可能性就大一些。
15.舞蹈
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。舞蹈类节目的签数量大于语言类节目的签数量,则抽到舞蹈类节目的可能性大。
【详解】6>4
陈芳同学从中抽出一个签,抽到舞蹈类节目的可能性大。
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
16. 1 5
【分析】要使掷出蓝色朝上的可能性比红色大,蓝色的面要比红色的面多,据此解答即可。
【详解】由分析可得:要使掷出蓝色朝上的可能性比红色大,红色涂1个面,蓝色涂5个面。(答案不唯一)
【点睛】根据可能性的大小,直接判断涂色面的多少,据此解答即可。
17.√
【分析】游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
【详解】有可能出“石头、剪刀、布”中的任何一个,三种结果赢的可能性相等。
所以,生活中用“石头、剪刀、布”决定输赢的方法是公平的。
原题说法正确;
故答案为:√
【点睛】本题考查游戏的公平性,明确要使游戏公平,发生的可能性必须相等。
18.×
【分析】比较白色部分和阴影部分,哪一部分所占的区域大,指针停在哪种区域的可能性就大;如果两部分区域一样大,则指针停在两部分的可能性一样大,据此分析。
【详解】由于图中白色部分与阴影部分相等,所以转动转盘,指针停在白色部分和阴影部分的可能性相等,原题说法错误。
故答案为:×
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种颜色的区域大,发生的可能性就大一些。
19.√
【分析】哪种牌面的数量越多,抽到的可能性就越大;两种牌面的数量同样多,抽到的可能性就一样大,据此分析。
【详解】一副完整的扑克牌有一个大王和一个小王,大王和小王的数量同样多,抽到大王的可能性和抽到小王的可能性一样大,原题说法正确。
故答案为:√
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种牌的数量多,发生的可能性就大一些。
20.×
【分析】确定事件包括必然事件和不可能事件:必然事件指在一定条件下,一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件,即随机事件是指在一定条件下,可能发生也可能不发生的事件。李叔叔买彩票中不中奖,属于不确定事件,有可能发生,也有可能不发生,据此解答即可。
【详解】李叔叔买了100张彩票,他有可能中奖,也有可能不中奖。原说法错误。
故答案为:×
【点睛】本题主要考查确定事件、不确定事件的定义。
21.见详解
【分析】盒子里全是黄球,摸到的一定是黄球;盒子里只要有黄球,就可能摸到黄球;盒子里只要有红球,就可能摸到红球;盒子里没有红球,不可能摸到红球;盒子里全是蓝求,一定摸到蓝球;盒子里只要有蓝球,就可能摸到蓝球;盒子里没有蓝球,不可能摸到蓝球;盒子里没有黄球,不可能摸到黄球,据此连线。
【详解】
【点睛】对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。
22.图见详解
【分析】图一白色区域面积远大于深色区域面积,所以指针很可能落在白色区域;
图二深色区域面积远大于白色区域,所以指针落在深色区域的可能性很大;
图三只有白色区域,所以指针一定停在白色区域,据此连线。
【详解】作图如下:
【点睛】本题考查了可能性,转盘上哪种颜色的区域面积大,指针落在该区域的可能性就大。
23.见详解
【分析】根据可能性大小的判断方法,想让小美赢的可能性大些,那么涂阴影区域要比白色区域多;
想让游戏公平,那么涂阴影区域和白色区域一样多,这样两人赢的可能性一样大。
【详解】如图:
(答案不唯一)
【点睛】本题考查可能性的大小,根据事件数量的多少判断可能性的大小。
24.见详解
【分析】(1)根据题意,摸出的一定是,要使事件一定发生,那么就要排除其他情况,只剩一种情况,也就是箱子里面就只有;
(2)摸出和的可能性一样大,也就是和的数量同样多即可。
【详解】(1)涂色如下:
(2)涂色如下:(涂法不唯一,两种颜色数量相等即可)
【点睛】此题考查了可能性的知识,关键能够结合数量情况改变可能性的大小。
25.第一个转盘:蓝色区域可能性最大,黄色区域可能性最小;第二个转盘:红色区域可能性最大,蓝色区域可能性最小
【分析】转盘上哪种颜色的区域最大,指针停在哪种颜色区域的可能性最大;哪种颜色的区域最小,指针停在哪种颜色区域的可能性最小。
【详解】第一个转盘,因为蓝色区域最大,所以指针停在蓝色区域的可能性最大,黄色区域最小,所以指针停在黄色区域的可能性最小;
第二个转盘,因为红色区域最大,所以指针停在红色区域的可能性最大,蓝色区域最小,所以指针停在蓝色区域的可能性最小。
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种颜色的区域大,发生的可能性就大一些。
26.蓝色、粉色、绿色或黄色
【分析】可能性的大小与区域的面积的大小有关,哪种颜色的区域的面积大,则停在该区域的可能性就大,反之就小;若每种颜色的区域的面积一样大,则停在这几种颜色区域的可能性一样大。
【详解】因为蓝色、粉色、绿色和黄色区域的面积一样大,则指针停在这四种区域的可能性一样大。
答:指针可能停在蓝色、粉色、绿色或黄色的区域上。
【点睛】本题考查可能性,明确可能性的大小与区域的面积的大小有关是解题的关键。
27.(1)可能摸出黄球,也可能摸出红球;(2)摸出黄球的可能性最大;摸出红球的可能性最小
【分析】(1)口袋里只有黄球和红球,一次摸出一个球,所以只可能摸出黄球或红球;
(2)不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。黄球的个数大于红球的个数,所以摸出黄球的可能性大于红球的可能性。
【详解】(1)一次摸出一个球,可能摸出黄球也可能摸出红球。
(2)8>2
黄球的个数大于红球的个数,
所以摸出黄球的可能性最大,摸出红球的可能性最小。
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
28.红球有9个,黑球有3个,图见详解
【分析】根据题意,要使摸出红球的可能性是摸出黑球可能性的3倍,如果红球有3,那么黑球有1,利用12除以(3+1)即可求出黑球的数量,再乘3即可求出红球的数量,再涂色即可。
【详解】12÷(3+1)
=12÷4
=3(个)
3×3=9(个)
如图:
【点睛】本题主要考查可能性的求法。
29.(1)见详解
(2)三等奖;三等奖占4份,占的份数最多,转动转盘时,指针停在三等奖区域的可能性最大,因此获三等奖的可能性最大。
【分析】(1)三等奖占4份,占的份数最多,转动转盘时,指针停在三等奖区域的可能性最大,据此作图即可。
(2)可能性的大小与所占区域的大小有关,区域越大则可能性越大,反之则小,据此解答。
【详解】(1)由分析可知,作图如下:
(2)三等奖;三等奖占4份,占的份数最多,转动转盘时,指针停在三等奖区域的可能性最大,因此获三等奖的可能性最大。
【点睛】本题考查可能性的大小,明确所占区域越大则可能性越大,反之则小是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
