人教版五年级数学上册第四单元可能性同步学案(知识点梳理+能力百分练)五
文档属性
| 名称 | 人教版五年级数学上册第四单元可能性同步学案(知识点梳理+能力百分练)五 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 06:27:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版五年级数学上册第四单元可能性(知识点梳理+能力百分练)五
知识点梳理
1、事件发生有确定性和不确定性,确定事件也就是一定会发生的或一定不会发生的事件,用“一定”、“不可能”来描述,不确定事件用“可能”来描述。
2、在游戏中,我们可以发现事件发生的可能性不同主要是受到了大小,数量,面积等原因,总结来说也就是某种情况在总数中所占比重越多,某一事件发生的可能性就越大。
3、设计与可能性相关的游戏时,先要知道游戏的所有可能性,再根据要求修改各种不同的事件发生的可能性。
能力百分练
一、选择题(共16分)
1.盒子里有9个红球、5个绿球,摸到可能性大的球是( )。
A.无法确定 B.红球 C.绿球 D.都一样
2.小明妈妈的年龄( )比小明大。
A.不可能 B.可能 C.一定 D.不能确定
3.方方和圆圆用转盘做游戏,指针停在红色区域算方方赢,停在蓝色区域算圆圆赢,停在黄色区域重新开始,用下面( )转盘做游戏对双方是公平的。
A. B.
C. D.
4.李明做摸球游戏,他任意摸了200次,摸到红球42次,黄球158次。根据数据推测,他最有可能是在装有( )的盒子里摸的。
A.10个红球 B.8个红球2个黄球
C.2个红球8个黄球 D.10个黄球
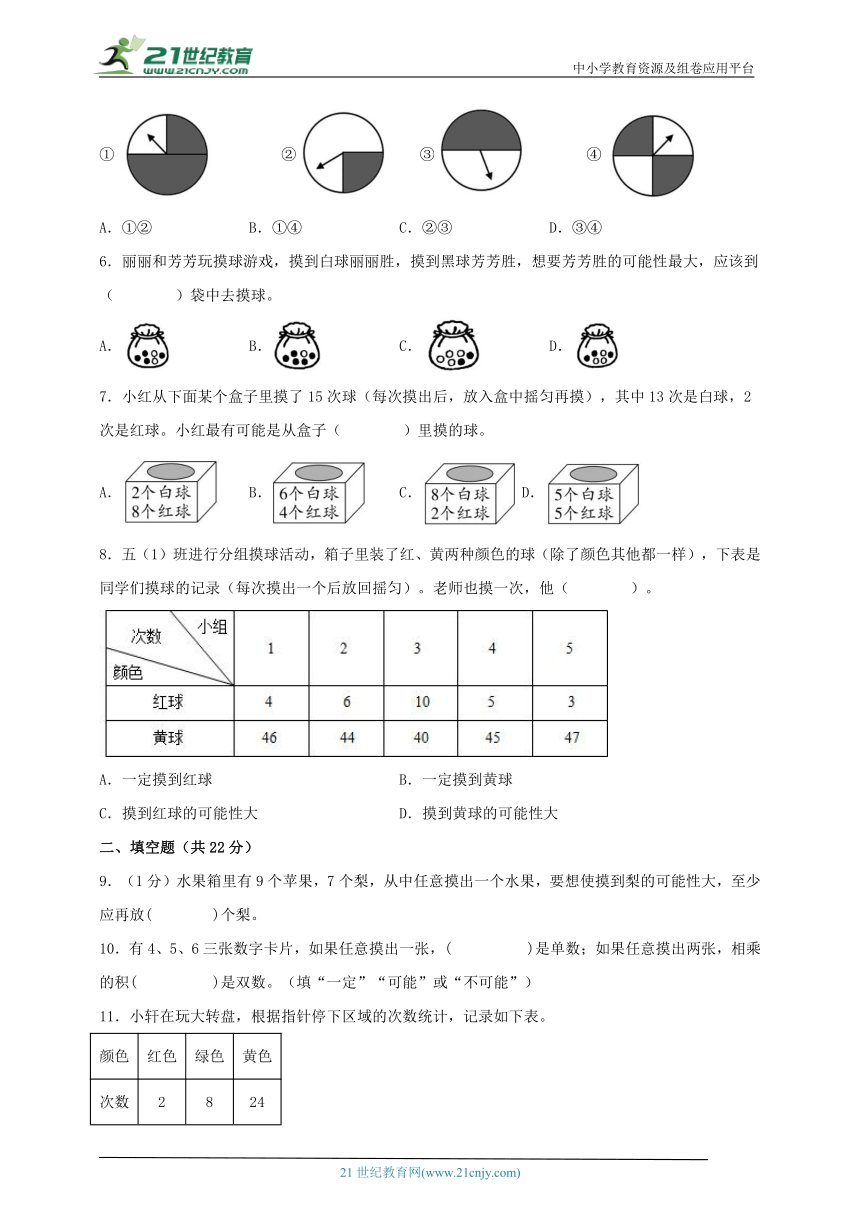
5.指针停在阴影区域可能性相等的是( )。
① ② ③ ④
A.①② B.①④ C.②③ D.③④
6.丽丽和芳芳玩摸球游戏,摸到白球丽丽胜,摸到黑球芳芳胜,想要芳芳胜的可能性最大,应该到( )袋中去摸球。
A. B. C. D.
7.小红从下面某个盒子里摸了15次球(每次摸出后,放入盒中摇匀再摸),其中13次是白球,2次是红球。小红最有可能是从盒子( )里摸的球。
A. B. C.D.
8.五(1)班进行分组摸球活动,箱子里装了红、黄两种颜色的球(除了颜色其他都一样),下表是同学们摸球的记录(每次摸出一个后放回摇匀)。老师也摸一次,他( )。
A.一定摸到红球 B.一定摸到黄球
C.摸到红球的可能性大 D.摸到黄球的可能性大
二、填空题(共22分)
9.(1分)水果箱里有9个苹果,7个梨,从中任意摸出一个水果,要想使摸到梨的可能性大,至少应再放( )个梨。
10.有4、5、6三张数字卡片,如果任意摸出一张,( )是单数;如果任意摸出两张,相乘的积( )是双数。(填“一定”“可能”或“不可能”)
11.小轩在玩大转盘,根据指针停下区域的次数统计,记录如下表。
颜色 红色 绿色 黄色
次数 2 8 24
根据表中的记录情况推测,大转盘上( )色区域最小。如果小轩再转30次,指针停在( )色区域的次数可能最多。
12.(5分)把10张卡片放纸袋内,随意摸一张,要使摸出数字“1”的可能性最小,数字“5”和“6”的可能性一样,卡片上可能是哪些数字?请你填一填。
13.(4分)用“可能”“不可能”或“一定”填空。
(1)从①号袋子里( )摸出黑球,( )摸出白球。
(2)从②号袋子里( )摸出黑球,( )摸出白球。
14.两位数乘两位数的积( )是两位数,( )是三位数。(用“一定”“可能”或“不可能”填空)。
15.(3分)如图:( )号桶里不可能摸出黑球;( )号桶里一定能摸出黑球;( )号桶里可能摸出白球。
16.(3分)袋子里放着6个苹果,3个橘子,2个桃子,9个梨,小朋随便拿出一个水果,出现的结果有( )种可能,拿到( )的可能性最大,要想让小朋随手拿到苹果的可能性最大,至少还要加( )个苹果。
三、判断题(共8分)
17.当游戏双方获胜的机会是均等时,游戏规则对双方才是公平的。( )
18.希望小学每年都举行校园足球联赛,连续四届五(5)班都是冠军,今年五(5)班一定是冠军。( )
19.一个路口的红绿灯时间设置为:红灯60秒,绿灯50秒,黄灯5秒,那么当你通过这个路口时,遇到红灯的可能性比较大。( )
20.在一次彩票有奖销售活动中,李叔叔买了100张彩票,一定能中奖。( )
四、连线题(共12分)
21.(6分)我会连。
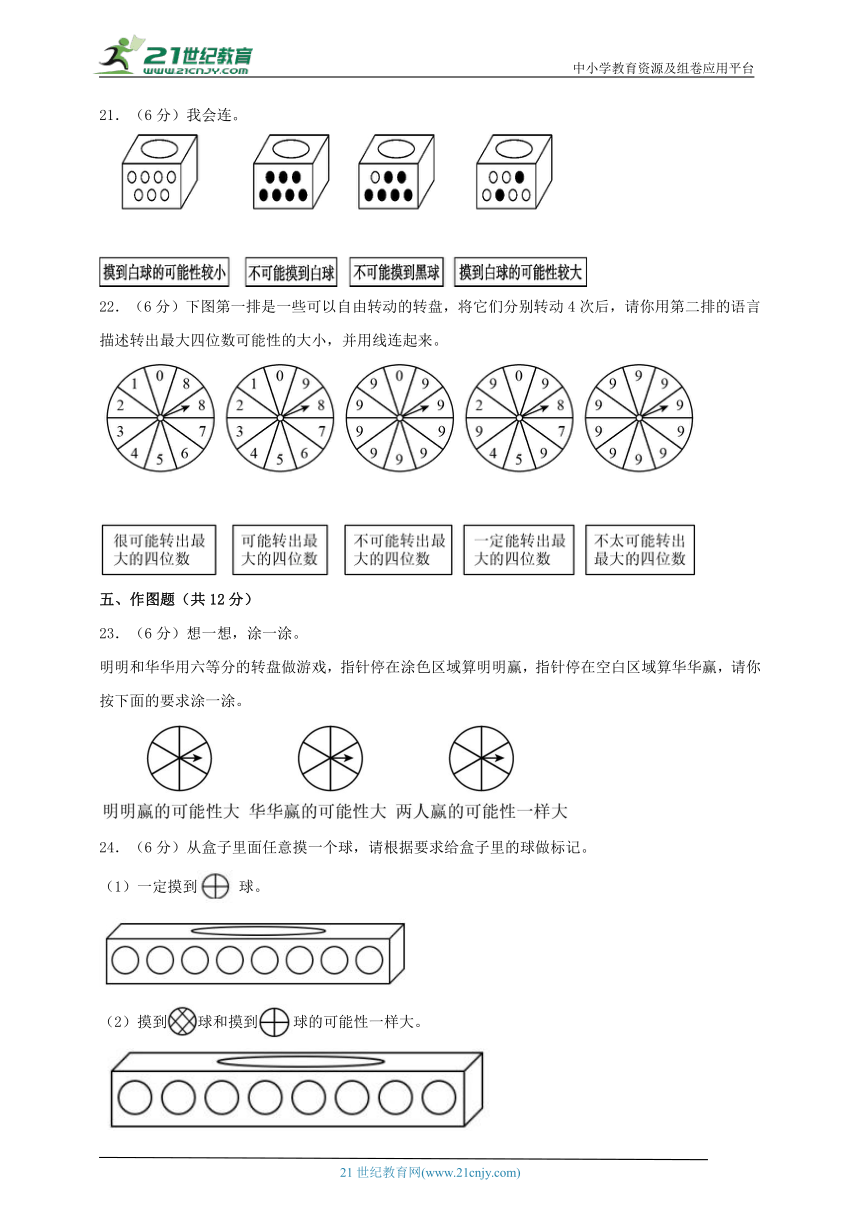
22.(6分)下图第一排是一些可以自由转动的转盘,将它们分别转动4次后,请你用第二排的语言描述转出最大四位数可能性的大小,并用线连起来。
五、作图题(共12分)
23.(6分)想一想,涂一涂。
明明和华华用六等分的转盘做游戏,指针停在涂色区域算明明赢,指针停在空白区域算华华赢,请你按下面的要求涂一涂。
24.(6分)从盒子里面任意摸一个球,请根据要求给盒子里的球做标记。
(1)一定摸到球。
(2)摸到球和摸到球的可能性一样大。
六、解答题(共30分)
25.(6分)给表面涂上红、蓝两种颜色,要使掷出红色面朝上的可能性比蓝色面大,应该怎么涂?
26.(6分)从下面9张卡片中抽出一张,最有可能抽到什么?
讲故事卡片 5张
唱歌卡片 3张
跳舞卡片 1张
27.(6分)小明和小丽玩转盘游戏,指针停在阴影区域算小明赢,指针停在白色区域算小丽赢。要想游戏公平,你会怎么设计转盘?请你涂一涂,并说明为什么是公平的?
28.(6分)桌子上有9张卡片,分别写着1—9个数,背面朝上,如果摸到单数,小丽赢,如果摸到双数,小明赢。
(1)这样约定公平吗?为什么?
(2)小明一定会输吗?
29.(6分)盒子里放有除颜色外完全相同的三种玻璃球,3颗红色的,2颗黄色的,1颗绿色的。
(1)淘气从盒子里任意摸出一颗玻璃球,可能是什么颜色的?有( )种可能,( )玻璃球可能性最大。
(2)笑笑从盒子里任意摸出其中一颗玻璃球,如果不区分颜色,有( )种可能。
(3)如果两个人轮流摸,摸后立即放回。摸到红球淘气赢,摸到其它颜色的球笑笑赢,请问这个游戏规则公平吗?请说明你的理由。
参考答案
1.B
【分析】根据可能性大小的判断方法,比较盒子里红球、绿球的数量多少,数量多的,摸到的可能性就大。
【详解】9>5
红球的数量多,所以摸到可能性大的球是红球。
故答案为:B
【点睛】本题考查可能性的大小,根据事件数量的多少判断可能性的大小。
2.C
【分析】一件事情可能发生也可能不发生,是不确定事件;
一件事情一定发生或不可能发生,是确定事件;据此判断。
【详解】小明妈妈的年龄一定会比小明大,这是一个客观事实,是一个确定的事件。
故答案为:C
【点睛】本题考查事件的确定性与不确定性。
3.B
【分析】转盘中红色区域和蓝色区域面积一样大的,停在红色和蓝色区域的可能性相等,对应游戏是公平的。据此解题。
【详解】A.停在红色区域的可能性大于停在蓝色区域的可能性,所以这个游戏不公平;
B.红色区域和蓝色区域面积相等,那么停在红色和蓝色区域的可能性相等,所以这个游戏是公平的;
C.停在蓝色区域的可能性大于停在红色区域的,所以这个游戏不公平;
D.停在红色区域的可能性大于停在蓝色区域的,所以这个游戏不公平。
故答案为:B
【点睛】本题考查了游戏规则的公平性,掌握可能性大小的判断方法是解题的关键。
4.C
【分析】逐项分析,根据条件判断可能性,用排除法求解。
【详解】A. 10个红球,不可能摸到黄球,不符合;
B. 8个红球2个黄球,红球多,摸到红球的可能性比黄球要大,不符合;
C. 2个红球8个黄球,黄球多,摸到黄球的可能性比红球要大,符合;
D. 10个黄球,不可能摸到红球,不符合。
故答案为:C
【点睛】本题主要考查可能性在生活中的应用。
5.D
【分析】图①的阴影区域占圆的四分之三,图②的阴影区域占圆的四分之一,图③的阴影区域占圆的二分之一,图④的阴影区域占圆的二分之一,若阴影部分一样大,则指针停在阴影区域的可能性一样大,据此解答。
【详解】图①的阴影区域占圆的四分之三,图②的阴影区域占圆的四分之一,图③的阴影区域占圆的二分之一,图④的阴影区域占圆的二分之一,图③④的阴影部分一样大,因此指针停在阴影区域的可能性就一样大。
故答案为:D
【点睛】考查事件发生的可能性大小,本题中有阴影和空白两个区域,阴影区域占圆的面积相同,则可能性就相同。
6.B
【分析】可能性的大小与球数量的多少有关,数量越多则被摸到的可能性就越大,反之就越小,据此逐一分析各项即可。
【详解】A.中黑球的数量多于白球,所以摸到黑球的可能性大,但与B项相比,黑球的数量比白球多的少一些;
B.中黑球的数量远多于白球,所以摸到黑球的可能性更大;
C.中白球的数量多于黑球,所以摸到白球的可能性大;
D.中白球和黑球的数量一样多,则摸到白球和黑球的可能性一样大。
故答案为:B
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
7.C
【分析】盒子里哪种球的数量多,摸到哪种球的可能性就大,哪种球的数量少,摸出哪种球的可能性就小,从摸出球的情况来看,摸出的白球比红球多得多,可能盒子里的白球比红球多得多,据此分析。
【详解】A.红球比白球多得多,摸出红球的可能性非常大,不符合题意;
B.白球比红球多一些,摸出白球的可能性大一些,不符合题意;
C.白球比红球多得多,摸出白球的可能性非常大,符合题意;
D.白球和红球同样多,摸出白球和红球的可能性一样大,不符合题意。
故答案为:C
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种球的数量多,发生的可能性就大一些。
8.D
【分析】因为盒子里有两种颜色的球,任意摸一个球,摸出什么颜色的球是不确定事件,不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,数量相同,可能性也相同。
【详解】第1组:4>46
第2组:6>44
第3组:10>40
第4组:5>45
第5组:3>47
因为盒子里摸到黄球的次数比摸到红球的次数多,所以老师再摸一次,选项中说法正确的是摸到黄球的可能性大。
故答案为:D
【点睛】本题解题关键是理解“摸出什么颜色的球是不确定事件”,理解并掌握影响可能性大小的因素,哪种颜色的球多,摸到哪种球的可能性就大。
9.3
【分析】要想使摸到梨的可能性大,则应使梨的数量多于苹果的数量,所以梨至少有10个,据此解答。
【详解】9-7+1
=2+1
=3(个)
则要想使摸到梨的可能性大,至少应再放3个梨。
【点睛】准确判断事件发生的可能性的大小是解答本题的关键。
10. 可能 一定
【分析】三张卡片任选一张有3种可能,其中4、6为双数,5为单数;所以:如果任意摸出一张,3种卡片都有可能,所以可能摸出单数,可能摸出双数;任意摸出两张则至少有一张是双数,据此列举如下:假设这个双数是4,另一个数可能是5,可能是6,可得:4×5=20,4×6=24;假设这个双数是6,另一个数可能是5,可能是4,可得:6×5=30,6×4=24;据此解题即可。
【详解】4×5=20
4×6=24
6×5=30
6×4=24
所以,有4、5、6三张数字卡片,如果任意摸出一张,可能是单数;如果任意摸出两张,相乘的积一定是双数。(填“一定”“可能”或“不可能”)
【点睛】本题主要考查可能性问题,能够列举出乘积的可能情况是解题的关键。
11. 红 黄
【分析】根据统计表可知,指针停下颜色区域的次数越多转盘上颜色区域就越大,指针停下颜色区域的次数越少转盘上颜色区域就越小;据此解答。
【详解】红色出现的次数最少,也就是可能性最小,大转盘上的区域也就最小;黄色出现的次数最多,也就是可能性最大,大转盘上的区域也就最大;
所以,根据表中的记录情况推测,大转盘上(红)色区域最小。如果小轩再转30次,指针停在(黄)色区域的次数可能最多。
【点睛】此题考查了可能性的大小,关键能够结合次数来判断颜色区域大小。
12.见详解
【分析】要想摸出“1”的可能性最小,“1”的张数最少,要想摸出“5”和“6”的可能性相等,则“5”和“6”的张数相等;由此解答即可。
【详解】由题意可知,这些卡片可能是“1”、“5”、“6”数字,且“1”最小,“5”和“6”一样多,如图:
【点睛】要想摸到哪个数字的可能性最大,该数字的张数必须最多,反之,该数字的张数最少,要想摸到哪两个数字的可能性相等,这两种数字的张数必须相等。此题答案不唯一。
13.(1) 可能 可能
(2) 一定 不可能
【分析】(1)根据袋子里球的颜色种类确定任意摸出球的可能,①号袋子有黑球,也有白球,所以有可能摸出黑球,也有可能摸出白球;
(2)②号袋子只有黑球,没有白球,所以一定能摸出黑球,不可能摸出白球。
【详解】(1)从①号袋子里可能摸出黑球,可能摸出白球。
(2)从②号袋子里一定能摸出黑球,不可能摸出白球。
【点睛】此题考查了可能性的大小,根据颜色的种类来确定。
14. 不可能 可能
【分析】根据题意,可以假设这两个两位数是最小的两位数,或者最大的两位数,然后再进行判断即可。
【详解】根据题意,假设这两个两位数是最小的两位数,即都是10,
那么10×10=100
100是三位数,
假设这两个两位数是最大的两位数,即都是99,
那么,99×99=9801
9801是四位数,
所以,两位数乘两位数,积不可能是两位数,可能是三位数。
【点睛】本题用赋值法能比较容易解决此类问题。
15. 2 1 3
【分析】可能性的大小与数量的多少有关,数量多则可能性就大,反之就小;1号桶中都是黑球,则一定能摸出黑球;2号桶中都是白球,则一定能摸出白球,不可能摸出黑球;3号桶中既有白球又有黑球,则可能摸出白球也可能摸出黑球。
【详解】由分析可知:
2号桶里不可能摸出黑球;1号桶里一定能摸出黑球;3号桶里可能摸出白球。
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
16. 4 梨 4
【分析】袋子中放着苹果、橘子、桃子和梨,小朋随便拿出一个水果,可能是这4种水果的其中一种,则有4种可能;根据可能性的大小与数量的多少有关,数量多的水果,被拿到的可能性就大,反之就小;要想让小朋随手拿到苹果的可能性最大,则应使苹果的数量最多。据此解答即可。
【详解】袋子里放着6个苹果,3个橘子,2个桃子,9个梨,小朋随便拿出一个水果,则可能是苹果、橘子、桃子、梨,也就是共有4种可能;
9>6>3>2
则小朋随便拿出一个水果,拿到梨的可能性最大
9-6+1
=3+1
=4(个)
则要想让小朋随手拿到苹果的可能性最大,至少还要加4个苹果。
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
17.√
【分析】当游戏双方获胜的机会是均等时,也就是说参与游戏双方获胜的可能性的大小相等;确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平;据此解答。
【详解】当游戏双方获胜的机会是均等时,也就是说参与游戏双方获胜的可能性的大小相等,所以游戏规则对双方是公平的,因此原题干的说法是正确的。
故答案为:√
【点睛】解答本题的关键是理解双方获胜的机会是均等时,也就是说游戏双方获胜的可能性的大小相等。
18.×
【分析】无论在什么情况下,都会发生的事件,是“一定”会发生的事件。在任何情况下,都不会发生的事件,是“不可能”事件。在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。据此解答。
【详解】虽然连续四届五(5)班都是冠军,但今年五(5)班能不能得冠军并不确定,所以今年五(5)班可能是冠军,题干中的说法是错误的。
故答案为:×
【点睛】此题主要考查事件的确定性与不确定性,对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。
19.√
【分析】哪种颜色的信号灯持续的时间长,遇到的可能性就大,反之即小,据此解答。
【详解】因为60>50>5
则当你通过这个路口时,遇到红灯的可能性比较大。原题干说法正确。
故答案为:√
【点睛】在不需要计算出可能性大小的准确值时,根据事件数量的多少进行判断即可。
20.×
【分析】确定事件包括必然事件和不可能事件:必然事件指在一定条件下,一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件,即随机事件是指在一定条件下,可能发生也可能不发生的事件。李叔叔买彩票中不中奖,属于不确定事件,有可能发生,也有可能不发生,据此解答即可。
【详解】李叔叔买了100张彩票,他有可能中奖,也有可能不中奖。原说法错误。
故答案为:×
【点睛】本题主要考查确定事件、不确定事件的定义。
21.见详解
【分析】盒子里哪种颜色球的数量越多,摸到该种颜色球的可能性就越大;盒子里哪种颜色球的数量越少,摸到该种颜色球的可能性就越小;如果盒子里没有该种颜色的球,那么不可能摸到该种颜色的球,据此解答。
【详解】分析可知:
【点睛】本题主要考查可能性,摸到该种颜色球的可能性的大小与该种颜色球的数量有关。
22.见详解
【分析】最大的四位数是9999。
第一个转盘内没有9,那么不可能转出最大的四位数;
第二个转盘内只有一个9,转出最大的四位数的可能性比较小;
第三个转盘内有9个9,1个0,很有可能转出最大的四位数;
第四个转盘内有3个9,可能转出最大的四位数;
第五个转盘内全部是9,一定能转出最大的四位数。
【详解】第一个转盘不可能转出最大的四位数;
第二个转盘不太可能转出最大的四位数;
第三个转盘很可能转出最大的四位数;
第四个转盘可能转出最大的四位数;
第五个转盘一定能转出最大的四位数。
连线如下:
【点睛】本题考查了可能性的大小,掌握可能性大小的判断方法是解题的关键。
23.见详解
【分析】根据各种区域面积的大小,直接判断可能性的大小;如果明明赢的可能性大,则涂色区域的面积大;反之,如果华华赢的可能性大则白色区域的面积大;如果使游戏最公平,则应把两种颜色的区域涂得面积相等;据此涂色即可。
【详解】如图:
(涂法不唯一)
【点睛】本题考查可能性的大小,解决此类问题的关键是分两种情况:(1)需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答;(2)不需要计算可能性的大小的准确值时,可以根据各种区域面积的大小,直接判断可能性的大小。
24.(1)见详解;(2)见详解
【分析】(1)根据“一定摸到球”,说明这个盒子里面的球全部是球。
(2)根据“摸到球和摸到球的可能性一样大”,说明两种球一样多。
【详解】(1)一定摸到球,如图:
(2)摸到球和摸到球的可能性一样大,如图:
【点睛】正确理解“一定”、“可能”、“不可能”表示的含义,根据这个含义求解。
25.5面红1面蓝或4面红2面蓝
【分析】有6个面,只要涂上的颜色红色比蓝色多,掷出红色面朝上的可能性就比蓝色面大,据此分析。
【详解】6=1+5=2+4=3+3
答:5面涂红色、1面涂蓝色,或者4面涂红色,2面涂蓝色。
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种颜色多,发生的可能性就大一些。
26.讲故事卡片
【分析】可能性的大小与卡片的数量的多少有关,哪种卡片的数量多,则被抽到的可能性就大,反之就小,据此解答即可。
【详解】因为5>3>1
答:从9张卡片中抽出一张,最有可能抽到讲故事卡片。
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
27.见解析
【分析】要想游戏公平,涂的阴影区域和白色区域一样多即可,共平均分成8份,阴影区域涂4份,据此解答问题。
【详解】8÷2=4(份)
设计如下图,涂的阴影区域和白色区域一样多,转转盘时,指针停在阴影区域和停在白色区域的可能性相同,所以游戏是公平的。(涂色情况不唯一,任意涂其中4份即可)
【点睛】解答此类问题的关键是要明确想要游戏公平,即停留两种区域的可能性相同,只需要保证两种区域的面积相同即可。
28.(1)不公平;摸到单数的可能性大
(2)不一定
【分析】(1)确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
(2)可能性大不一定会发生,可能性小也可能会发生,据此分析。
【详解】(1)1—9中,单数有:1、3、5、7、9,共5个,双数有:2、4、6、8,共4个,5>4。
答:这样的约定不公平,单数多,双数少,摸到单数的可能性大。
(2)小明不一定会输,单数多,只是说明小丽赢的可能性大一些,也有可能摸到双数,只要有可能摸到双数,小明就有可能赢。
【点睛】游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。
29.(1)3;红色
(2)6
(3)公平,理由见详解
【分析】(1)盒子里有几种颜色的球,就有几种可能摸出的结果;比较各种颜色球的数量,哪种颜色球的数量最多,摸到的可能性最大。
(2)不区分颜色,所有球都有可能摸出,共有几颗球,摸出的结果就有几种可能。
(3)确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
【详解】(1)盒子里有红、黄、绿,3种颜色的球,任意摸出一颗玻璃球,有3种可能;3>2>1,红色玻璃球可能性最大。
(2)3+2+1=6(颗),如果不区分颜色,有6种可能。
(3)2+1=3(颗)
3=3
答:这个游戏规则公平,因为红球和其它颜色球的总数量一样。
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种球多,发生的可能性就大一些。游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版五年级数学上册第四单元可能性(知识点梳理+能力百分练)五
知识点梳理
1、事件发生有确定性和不确定性,确定事件也就是一定会发生的或一定不会发生的事件,用“一定”、“不可能”来描述,不确定事件用“可能”来描述。
2、在游戏中,我们可以发现事件发生的可能性不同主要是受到了大小,数量,面积等原因,总结来说也就是某种情况在总数中所占比重越多,某一事件发生的可能性就越大。
3、设计与可能性相关的游戏时,先要知道游戏的所有可能性,再根据要求修改各种不同的事件发生的可能性。
能力百分练
一、选择题(共16分)
1.盒子里有9个红球、5个绿球,摸到可能性大的球是( )。
A.无法确定 B.红球 C.绿球 D.都一样
2.小明妈妈的年龄( )比小明大。
A.不可能 B.可能 C.一定 D.不能确定
3.方方和圆圆用转盘做游戏,指针停在红色区域算方方赢,停在蓝色区域算圆圆赢,停在黄色区域重新开始,用下面( )转盘做游戏对双方是公平的。
A. B.
C. D.
4.李明做摸球游戏,他任意摸了200次,摸到红球42次,黄球158次。根据数据推测,他最有可能是在装有( )的盒子里摸的。
A.10个红球 B.8个红球2个黄球
C.2个红球8个黄球 D.10个黄球
5.指针停在阴影区域可能性相等的是( )。
① ② ③ ④
A.①② B.①④ C.②③ D.③④
6.丽丽和芳芳玩摸球游戏,摸到白球丽丽胜,摸到黑球芳芳胜,想要芳芳胜的可能性最大,应该到( )袋中去摸球。
A. B. C. D.
7.小红从下面某个盒子里摸了15次球(每次摸出后,放入盒中摇匀再摸),其中13次是白球,2次是红球。小红最有可能是从盒子( )里摸的球。
A. B. C.D.
8.五(1)班进行分组摸球活动,箱子里装了红、黄两种颜色的球(除了颜色其他都一样),下表是同学们摸球的记录(每次摸出一个后放回摇匀)。老师也摸一次,他( )。
A.一定摸到红球 B.一定摸到黄球
C.摸到红球的可能性大 D.摸到黄球的可能性大
二、填空题(共22分)
9.(1分)水果箱里有9个苹果,7个梨,从中任意摸出一个水果,要想使摸到梨的可能性大,至少应再放( )个梨。
10.有4、5、6三张数字卡片,如果任意摸出一张,( )是单数;如果任意摸出两张,相乘的积( )是双数。(填“一定”“可能”或“不可能”)
11.小轩在玩大转盘,根据指针停下区域的次数统计,记录如下表。
颜色 红色 绿色 黄色
次数 2 8 24
根据表中的记录情况推测,大转盘上( )色区域最小。如果小轩再转30次,指针停在( )色区域的次数可能最多。
12.(5分)把10张卡片放纸袋内,随意摸一张,要使摸出数字“1”的可能性最小,数字“5”和“6”的可能性一样,卡片上可能是哪些数字?请你填一填。
13.(4分)用“可能”“不可能”或“一定”填空。
(1)从①号袋子里( )摸出黑球,( )摸出白球。
(2)从②号袋子里( )摸出黑球,( )摸出白球。
14.两位数乘两位数的积( )是两位数,( )是三位数。(用“一定”“可能”或“不可能”填空)。
15.(3分)如图:( )号桶里不可能摸出黑球;( )号桶里一定能摸出黑球;( )号桶里可能摸出白球。
16.(3分)袋子里放着6个苹果,3个橘子,2个桃子,9个梨,小朋随便拿出一个水果,出现的结果有( )种可能,拿到( )的可能性最大,要想让小朋随手拿到苹果的可能性最大,至少还要加( )个苹果。
三、判断题(共8分)
17.当游戏双方获胜的机会是均等时,游戏规则对双方才是公平的。( )
18.希望小学每年都举行校园足球联赛,连续四届五(5)班都是冠军,今年五(5)班一定是冠军。( )
19.一个路口的红绿灯时间设置为:红灯60秒,绿灯50秒,黄灯5秒,那么当你通过这个路口时,遇到红灯的可能性比较大。( )
20.在一次彩票有奖销售活动中,李叔叔买了100张彩票,一定能中奖。( )
四、连线题(共12分)
21.(6分)我会连。
22.(6分)下图第一排是一些可以自由转动的转盘,将它们分别转动4次后,请你用第二排的语言描述转出最大四位数可能性的大小,并用线连起来。
五、作图题(共12分)
23.(6分)想一想,涂一涂。
明明和华华用六等分的转盘做游戏,指针停在涂色区域算明明赢,指针停在空白区域算华华赢,请你按下面的要求涂一涂。
24.(6分)从盒子里面任意摸一个球,请根据要求给盒子里的球做标记。
(1)一定摸到球。
(2)摸到球和摸到球的可能性一样大。
六、解答题(共30分)
25.(6分)给表面涂上红、蓝两种颜色,要使掷出红色面朝上的可能性比蓝色面大,应该怎么涂?
26.(6分)从下面9张卡片中抽出一张,最有可能抽到什么?
讲故事卡片 5张
唱歌卡片 3张
跳舞卡片 1张
27.(6分)小明和小丽玩转盘游戏,指针停在阴影区域算小明赢,指针停在白色区域算小丽赢。要想游戏公平,你会怎么设计转盘?请你涂一涂,并说明为什么是公平的?
28.(6分)桌子上有9张卡片,分别写着1—9个数,背面朝上,如果摸到单数,小丽赢,如果摸到双数,小明赢。
(1)这样约定公平吗?为什么?
(2)小明一定会输吗?
29.(6分)盒子里放有除颜色外完全相同的三种玻璃球,3颗红色的,2颗黄色的,1颗绿色的。
(1)淘气从盒子里任意摸出一颗玻璃球,可能是什么颜色的?有( )种可能,( )玻璃球可能性最大。
(2)笑笑从盒子里任意摸出其中一颗玻璃球,如果不区分颜色,有( )种可能。
(3)如果两个人轮流摸,摸后立即放回。摸到红球淘气赢,摸到其它颜色的球笑笑赢,请问这个游戏规则公平吗?请说明你的理由。
参考答案
1.B
【分析】根据可能性大小的判断方法,比较盒子里红球、绿球的数量多少,数量多的,摸到的可能性就大。
【详解】9>5
红球的数量多,所以摸到可能性大的球是红球。
故答案为:B
【点睛】本题考查可能性的大小,根据事件数量的多少判断可能性的大小。
2.C
【分析】一件事情可能发生也可能不发生,是不确定事件;
一件事情一定发生或不可能发生,是确定事件;据此判断。
【详解】小明妈妈的年龄一定会比小明大,这是一个客观事实,是一个确定的事件。
故答案为:C
【点睛】本题考查事件的确定性与不确定性。
3.B
【分析】转盘中红色区域和蓝色区域面积一样大的,停在红色和蓝色区域的可能性相等,对应游戏是公平的。据此解题。
【详解】A.停在红色区域的可能性大于停在蓝色区域的可能性,所以这个游戏不公平;
B.红色区域和蓝色区域面积相等,那么停在红色和蓝色区域的可能性相等,所以这个游戏是公平的;
C.停在蓝色区域的可能性大于停在红色区域的,所以这个游戏不公平;
D.停在红色区域的可能性大于停在蓝色区域的,所以这个游戏不公平。
故答案为:B
【点睛】本题考查了游戏规则的公平性,掌握可能性大小的判断方法是解题的关键。
4.C
【分析】逐项分析,根据条件判断可能性,用排除法求解。
【详解】A. 10个红球,不可能摸到黄球,不符合;
B. 8个红球2个黄球,红球多,摸到红球的可能性比黄球要大,不符合;
C. 2个红球8个黄球,黄球多,摸到黄球的可能性比红球要大,符合;
D. 10个黄球,不可能摸到红球,不符合。
故答案为:C
【点睛】本题主要考查可能性在生活中的应用。
5.D
【分析】图①的阴影区域占圆的四分之三,图②的阴影区域占圆的四分之一,图③的阴影区域占圆的二分之一,图④的阴影区域占圆的二分之一,若阴影部分一样大,则指针停在阴影区域的可能性一样大,据此解答。
【详解】图①的阴影区域占圆的四分之三,图②的阴影区域占圆的四分之一,图③的阴影区域占圆的二分之一,图④的阴影区域占圆的二分之一,图③④的阴影部分一样大,因此指针停在阴影区域的可能性就一样大。
故答案为:D
【点睛】考查事件发生的可能性大小,本题中有阴影和空白两个区域,阴影区域占圆的面积相同,则可能性就相同。
6.B
【分析】可能性的大小与球数量的多少有关,数量越多则被摸到的可能性就越大,反之就越小,据此逐一分析各项即可。
【详解】A.中黑球的数量多于白球,所以摸到黑球的可能性大,但与B项相比,黑球的数量比白球多的少一些;
B.中黑球的数量远多于白球,所以摸到黑球的可能性更大;
C.中白球的数量多于黑球,所以摸到白球的可能性大;
D.中白球和黑球的数量一样多,则摸到白球和黑球的可能性一样大。
故答案为:B
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
7.C
【分析】盒子里哪种球的数量多,摸到哪种球的可能性就大,哪种球的数量少,摸出哪种球的可能性就小,从摸出球的情况来看,摸出的白球比红球多得多,可能盒子里的白球比红球多得多,据此分析。
【详解】A.红球比白球多得多,摸出红球的可能性非常大,不符合题意;
B.白球比红球多一些,摸出白球的可能性大一些,不符合题意;
C.白球比红球多得多,摸出白球的可能性非常大,符合题意;
D.白球和红球同样多,摸出白球和红球的可能性一样大,不符合题意。
故答案为:C
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种球的数量多,发生的可能性就大一些。
8.D
【分析】因为盒子里有两种颜色的球,任意摸一个球,摸出什么颜色的球是不确定事件,不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,数量相同,可能性也相同。
【详解】第1组:4>46
第2组:6>44
第3组:10>40
第4组:5>45
第5组:3>47
因为盒子里摸到黄球的次数比摸到红球的次数多,所以老师再摸一次,选项中说法正确的是摸到黄球的可能性大。
故答案为:D
【点睛】本题解题关键是理解“摸出什么颜色的球是不确定事件”,理解并掌握影响可能性大小的因素,哪种颜色的球多,摸到哪种球的可能性就大。
9.3
【分析】要想使摸到梨的可能性大,则应使梨的数量多于苹果的数量,所以梨至少有10个,据此解答。
【详解】9-7+1
=2+1
=3(个)
则要想使摸到梨的可能性大,至少应再放3个梨。
【点睛】准确判断事件发生的可能性的大小是解答本题的关键。
10. 可能 一定
【分析】三张卡片任选一张有3种可能,其中4、6为双数,5为单数;所以:如果任意摸出一张,3种卡片都有可能,所以可能摸出单数,可能摸出双数;任意摸出两张则至少有一张是双数,据此列举如下:假设这个双数是4,另一个数可能是5,可能是6,可得:4×5=20,4×6=24;假设这个双数是6,另一个数可能是5,可能是4,可得:6×5=30,6×4=24;据此解题即可。
【详解】4×5=20
4×6=24
6×5=30
6×4=24
所以,有4、5、6三张数字卡片,如果任意摸出一张,可能是单数;如果任意摸出两张,相乘的积一定是双数。(填“一定”“可能”或“不可能”)
【点睛】本题主要考查可能性问题,能够列举出乘积的可能情况是解题的关键。
11. 红 黄
【分析】根据统计表可知,指针停下颜色区域的次数越多转盘上颜色区域就越大,指针停下颜色区域的次数越少转盘上颜色区域就越小;据此解答。
【详解】红色出现的次数最少,也就是可能性最小,大转盘上的区域也就最小;黄色出现的次数最多,也就是可能性最大,大转盘上的区域也就最大;
所以,根据表中的记录情况推测,大转盘上(红)色区域最小。如果小轩再转30次,指针停在(黄)色区域的次数可能最多。
【点睛】此题考查了可能性的大小,关键能够结合次数来判断颜色区域大小。
12.见详解
【分析】要想摸出“1”的可能性最小,“1”的张数最少,要想摸出“5”和“6”的可能性相等,则“5”和“6”的张数相等;由此解答即可。
【详解】由题意可知,这些卡片可能是“1”、“5”、“6”数字,且“1”最小,“5”和“6”一样多,如图:
【点睛】要想摸到哪个数字的可能性最大,该数字的张数必须最多,反之,该数字的张数最少,要想摸到哪两个数字的可能性相等,这两种数字的张数必须相等。此题答案不唯一。
13.(1) 可能 可能
(2) 一定 不可能
【分析】(1)根据袋子里球的颜色种类确定任意摸出球的可能,①号袋子有黑球,也有白球,所以有可能摸出黑球,也有可能摸出白球;
(2)②号袋子只有黑球,没有白球,所以一定能摸出黑球,不可能摸出白球。
【详解】(1)从①号袋子里可能摸出黑球,可能摸出白球。
(2)从②号袋子里一定能摸出黑球,不可能摸出白球。
【点睛】此题考查了可能性的大小,根据颜色的种类来确定。
14. 不可能 可能
【分析】根据题意,可以假设这两个两位数是最小的两位数,或者最大的两位数,然后再进行判断即可。
【详解】根据题意,假设这两个两位数是最小的两位数,即都是10,
那么10×10=100
100是三位数,
假设这两个两位数是最大的两位数,即都是99,
那么,99×99=9801
9801是四位数,
所以,两位数乘两位数,积不可能是两位数,可能是三位数。
【点睛】本题用赋值法能比较容易解决此类问题。
15. 2 1 3
【分析】可能性的大小与数量的多少有关,数量多则可能性就大,反之就小;1号桶中都是黑球,则一定能摸出黑球;2号桶中都是白球,则一定能摸出白球,不可能摸出黑球;3号桶中既有白球又有黑球,则可能摸出白球也可能摸出黑球。
【详解】由分析可知:
2号桶里不可能摸出黑球;1号桶里一定能摸出黑球;3号桶里可能摸出白球。
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
16. 4 梨 4
【分析】袋子中放着苹果、橘子、桃子和梨,小朋随便拿出一个水果,可能是这4种水果的其中一种,则有4种可能;根据可能性的大小与数量的多少有关,数量多的水果,被拿到的可能性就大,反之就小;要想让小朋随手拿到苹果的可能性最大,则应使苹果的数量最多。据此解答即可。
【详解】袋子里放着6个苹果,3个橘子,2个桃子,9个梨,小朋随便拿出一个水果,则可能是苹果、橘子、桃子、梨,也就是共有4种可能;
9>6>3>2
则小朋随便拿出一个水果,拿到梨的可能性最大
9-6+1
=3+1
=4(个)
则要想让小朋随手拿到苹果的可能性最大,至少还要加4个苹果。
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
17.√
【分析】当游戏双方获胜的机会是均等时,也就是说参与游戏双方获胜的可能性的大小相等;确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平;据此解答。
【详解】当游戏双方获胜的机会是均等时,也就是说参与游戏双方获胜的可能性的大小相等,所以游戏规则对双方是公平的,因此原题干的说法是正确的。
故答案为:√
【点睛】解答本题的关键是理解双方获胜的机会是均等时,也就是说游戏双方获胜的可能性的大小相等。
18.×
【分析】无论在什么情况下,都会发生的事件,是“一定”会发生的事件。在任何情况下,都不会发生的事件,是“不可能”事件。在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。据此解答。
【详解】虽然连续四届五(5)班都是冠军,但今年五(5)班能不能得冠军并不确定,所以今年五(5)班可能是冠军,题干中的说法是错误的。
故答案为:×
【点睛】此题主要考查事件的确定性与不确定性,对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。
19.√
【分析】哪种颜色的信号灯持续的时间长,遇到的可能性就大,反之即小,据此解答。
【详解】因为60>50>5
则当你通过这个路口时,遇到红灯的可能性比较大。原题干说法正确。
故答案为:√
【点睛】在不需要计算出可能性大小的准确值时,根据事件数量的多少进行判断即可。
20.×
【分析】确定事件包括必然事件和不可能事件:必然事件指在一定条件下,一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件,即随机事件是指在一定条件下,可能发生也可能不发生的事件。李叔叔买彩票中不中奖,属于不确定事件,有可能发生,也有可能不发生,据此解答即可。
【详解】李叔叔买了100张彩票,他有可能中奖,也有可能不中奖。原说法错误。
故答案为:×
【点睛】本题主要考查确定事件、不确定事件的定义。
21.见详解
【分析】盒子里哪种颜色球的数量越多,摸到该种颜色球的可能性就越大;盒子里哪种颜色球的数量越少,摸到该种颜色球的可能性就越小;如果盒子里没有该种颜色的球,那么不可能摸到该种颜色的球,据此解答。
【详解】分析可知:
【点睛】本题主要考查可能性,摸到该种颜色球的可能性的大小与该种颜色球的数量有关。
22.见详解
【分析】最大的四位数是9999。
第一个转盘内没有9,那么不可能转出最大的四位数;
第二个转盘内只有一个9,转出最大的四位数的可能性比较小;
第三个转盘内有9个9,1个0,很有可能转出最大的四位数;
第四个转盘内有3个9,可能转出最大的四位数;
第五个转盘内全部是9,一定能转出最大的四位数。
【详解】第一个转盘不可能转出最大的四位数;
第二个转盘不太可能转出最大的四位数;
第三个转盘很可能转出最大的四位数;
第四个转盘可能转出最大的四位数;
第五个转盘一定能转出最大的四位数。
连线如下:
【点睛】本题考查了可能性的大小,掌握可能性大小的判断方法是解题的关键。
23.见详解
【分析】根据各种区域面积的大小,直接判断可能性的大小;如果明明赢的可能性大,则涂色区域的面积大;反之,如果华华赢的可能性大则白色区域的面积大;如果使游戏最公平,则应把两种颜色的区域涂得面积相等;据此涂色即可。
【详解】如图:
(涂法不唯一)
【点睛】本题考查可能性的大小,解决此类问题的关键是分两种情况:(1)需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答;(2)不需要计算可能性的大小的准确值时,可以根据各种区域面积的大小,直接判断可能性的大小。
24.(1)见详解;(2)见详解
【分析】(1)根据“一定摸到球”,说明这个盒子里面的球全部是球。
(2)根据“摸到球和摸到球的可能性一样大”,说明两种球一样多。
【详解】(1)一定摸到球,如图:
(2)摸到球和摸到球的可能性一样大,如图:
【点睛】正确理解“一定”、“可能”、“不可能”表示的含义,根据这个含义求解。
25.5面红1面蓝或4面红2面蓝
【分析】有6个面,只要涂上的颜色红色比蓝色多,掷出红色面朝上的可能性就比蓝色面大,据此分析。
【详解】6=1+5=2+4=3+3
答:5面涂红色、1面涂蓝色,或者4面涂红色,2面涂蓝色。
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种颜色多,发生的可能性就大一些。
26.讲故事卡片
【分析】可能性的大小与卡片的数量的多少有关,哪种卡片的数量多,则被抽到的可能性就大,反之就小,据此解答即可。
【详解】因为5>3>1
答:从9张卡片中抽出一张,最有可能抽到讲故事卡片。
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
27.见解析
【分析】要想游戏公平,涂的阴影区域和白色区域一样多即可,共平均分成8份,阴影区域涂4份,据此解答问题。
【详解】8÷2=4(份)
设计如下图,涂的阴影区域和白色区域一样多,转转盘时,指针停在阴影区域和停在白色区域的可能性相同,所以游戏是公平的。(涂色情况不唯一,任意涂其中4份即可)
【点睛】解答此类问题的关键是要明确想要游戏公平,即停留两种区域的可能性相同,只需要保证两种区域的面积相同即可。
28.(1)不公平;摸到单数的可能性大
(2)不一定
【分析】(1)确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
(2)可能性大不一定会发生,可能性小也可能会发生,据此分析。
【详解】(1)1—9中,单数有:1、3、5、7、9,共5个,双数有:2、4、6、8,共4个,5>4。
答:这样的约定不公平,单数多,双数少,摸到单数的可能性大。
(2)小明不一定会输,单数多,只是说明小丽赢的可能性大一些,也有可能摸到双数,只要有可能摸到双数,小明就有可能赢。
【点睛】游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。
29.(1)3;红色
(2)6
(3)公平,理由见详解
【分析】(1)盒子里有几种颜色的球,就有几种可能摸出的结果;比较各种颜色球的数量,哪种颜色球的数量最多,摸到的可能性最大。
(2)不区分颜色,所有球都有可能摸出,共有几颗球,摸出的结果就有几种可能。
(3)确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
【详解】(1)盒子里有红、黄、绿,3种颜色的球,任意摸出一颗玻璃球,有3种可能;3>2>1,红色玻璃球可能性最大。
(2)3+2+1=6(颗),如果不区分颜色,有6种可能。
(3)2+1=3(颗)
3=3
答:这个游戏规则公平,因为红球和其它颜色球的总数量一样。
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种球多,发生的可能性就大一些。游戏规则的公平性就是指对游戏的双方来说,机会是均等的,也就是双方获胜的可能性的大小相等。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
