沪教版三年级下册数学7.6《数学广场——搭配》课件(共14张PPT)
文档属性
| 名称 | 沪教版三年级下册数学7.6《数学广场——搭配》课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
《数学广场——搭配》
沪教版三年级下册
学校足球队有三种颜色的运动上衣和两种颜色的短裤。总共有几种搭配方案?
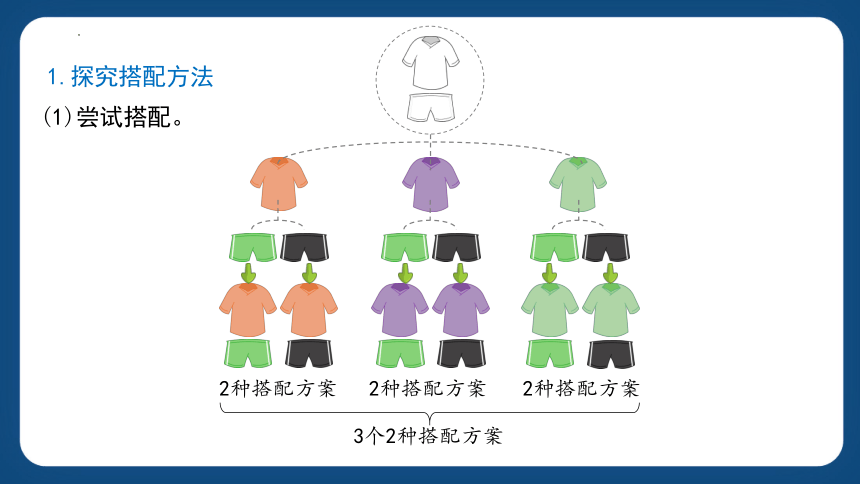
1.探究搭配方法
(1)尝试搭配。
2种搭配方案
2种搭配方案
2种搭配方案
3个2种搭配方案
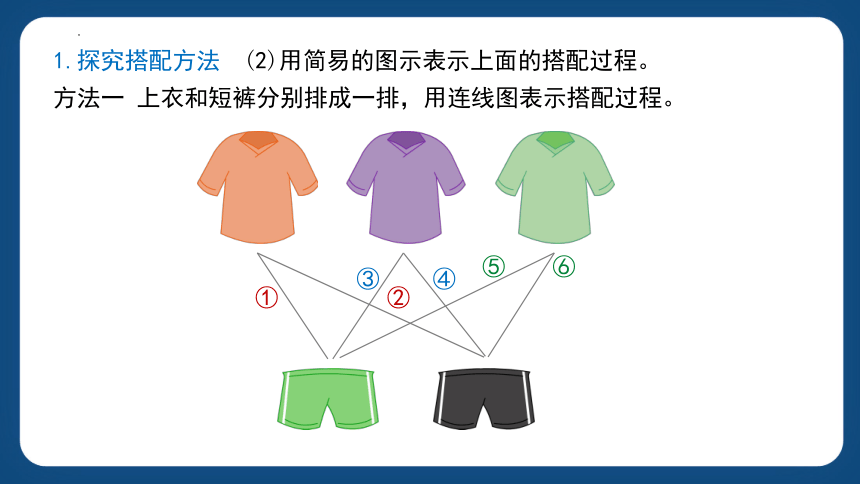
1.探究搭配方法
(2)用简易的图示表示上面的搭配过程。
方法一 上衣和短裤分别排成一排,用连线图表示搭配过程。
①
②
③
④
⑤
⑥
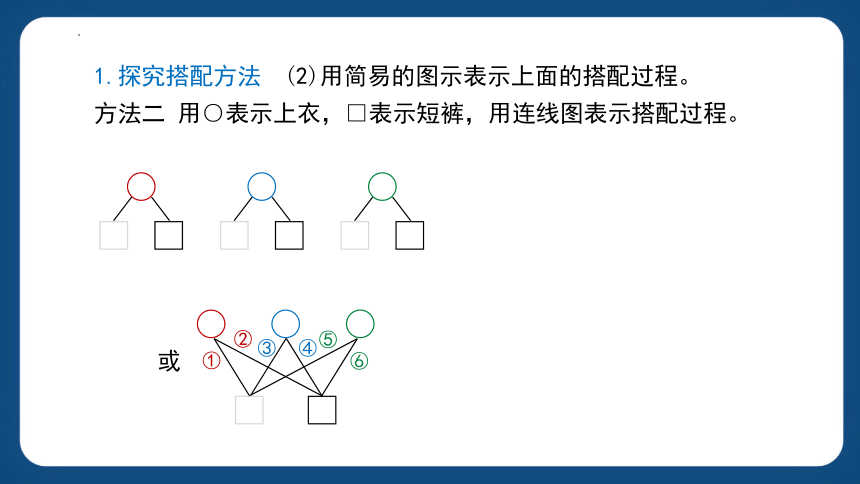
1.探究搭配方法
(2)用简易的图示表示上面的搭配过程。
方法二 用○表示上衣,□表示短裤,用连线图表示搭配过程。
或
①
②
③
④
⑤
⑥
2.观察搭配方法,寻找规律
无论是每件上衣与2件短裤进行搭配,还是每件短裤与3件上衣进行搭配,搭配在一起都有6种穿法。
从中得出:搭配方案的数量与上衣和短裤的件数有关,上衣和短裤件数的乘积就是搭配方案的数量,即把两类事物的数量相乘,就可得出一共有多少种搭配方案。
搭配上衣和短裤时,可以从不同的角度去思考,先固定上衣或短裤,可以用实物图或符号表示实物,再用连线的方法按顺序一一去搭配,求出搭配方案的数量。
在求上衣和短裤的搭配方案时,如果上衣有m件,短裤有n件,那么一共有mn种搭配方案。
六一儿童节,同学们用红色、绿色纸做灯笼。
灯笼有三层,每层只用一种颜色的纸。
一共有多少种不同颜色搭配的灯笼?
1.明确涂色方法
共有8种涂色方法。
涂色方法
2.观察搭配方法,寻找规律
(1)涂色时颜色位置的不同,灯笼的颜色就不同,
此种搭配方法属于排列问题。
(2)排列数的求法与乘法的联系。
例如完成涂色需要三步:第一步涂第一层,第二步涂第二层,第三步涂第三层。完成第一步有2种不同方法,完成第二步有2种不同方法,完成第三步有2种不同方法,完成涂色一共就有2×2×2种不同方法,即8种不同方法。
可以用图示求搭配的结果,在属于排列的搭配过程中,要做到有序搭配,先确定第一步的搭配方法,然后是第二步,依次类推,做到不重复、不遗漏。
1.有4个小朋友,每2个小朋友互相握手问好,一共要握多少次手?
练习
2.拉动纸条,可以组成哪些两位数?请你写一写。
3.小兔回家有几条路可以走?
《数学广场——搭配》
沪教版三年级下册
学校足球队有三种颜色的运动上衣和两种颜色的短裤。总共有几种搭配方案?
1.探究搭配方法
(1)尝试搭配。
2种搭配方案
2种搭配方案
2种搭配方案
3个2种搭配方案
1.探究搭配方法
(2)用简易的图示表示上面的搭配过程。
方法一 上衣和短裤分别排成一排,用连线图表示搭配过程。
①
②
③
④
⑤
⑥
1.探究搭配方法
(2)用简易的图示表示上面的搭配过程。
方法二 用○表示上衣,□表示短裤,用连线图表示搭配过程。
或
①
②
③
④
⑤
⑥
2.观察搭配方法,寻找规律
无论是每件上衣与2件短裤进行搭配,还是每件短裤与3件上衣进行搭配,搭配在一起都有6种穿法。
从中得出:搭配方案的数量与上衣和短裤的件数有关,上衣和短裤件数的乘积就是搭配方案的数量,即把两类事物的数量相乘,就可得出一共有多少种搭配方案。
搭配上衣和短裤时,可以从不同的角度去思考,先固定上衣或短裤,可以用实物图或符号表示实物,再用连线的方法按顺序一一去搭配,求出搭配方案的数量。
在求上衣和短裤的搭配方案时,如果上衣有m件,短裤有n件,那么一共有mn种搭配方案。
六一儿童节,同学们用红色、绿色纸做灯笼。
灯笼有三层,每层只用一种颜色的纸。
一共有多少种不同颜色搭配的灯笼?
1.明确涂色方法
共有8种涂色方法。
涂色方法
2.观察搭配方法,寻找规律
(1)涂色时颜色位置的不同,灯笼的颜色就不同,
此种搭配方法属于排列问题。
(2)排列数的求法与乘法的联系。
例如完成涂色需要三步:第一步涂第一层,第二步涂第二层,第三步涂第三层。完成第一步有2种不同方法,完成第二步有2种不同方法,完成第三步有2种不同方法,完成涂色一共就有2×2×2种不同方法,即8种不同方法。
可以用图示求搭配的结果,在属于排列的搭配过程中,要做到有序搭配,先确定第一步的搭配方法,然后是第二步,依次类推,做到不重复、不遗漏。
1.有4个小朋友,每2个小朋友互相握手问好,一共要握多少次手?
练习
2.拉动纸条,可以组成哪些两位数?请你写一写。
3.小兔回家有几条路可以走?
