2023—2024学年苏科版九年级数学下册7.5解直角三角形同步练习题(含解析)
文档属性
| 名称 | 2023—2024学年苏科版九年级数学下册7.5解直角三角形同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 248.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 15:04:48 | ||
图片预览



文档简介
2023-2024学年苏科版九年级数学下册《7.5解直角三角形》同步练习题(附答案)
一、单选题
1.在中,,当已知和a时,求c,应选择的关系式是( )
A. B. C. D.
2.在中,,,,则的长为( )
A.3 B.2 C. D.
3.某楼梯的侧面如图所示,已测得的长约为米,约为,则该楼梯的高度可表示为( )
A. B. C. D.
4.如图,在矩形中,,,对角线的垂直平分线分别交于点,则的长为( )
A. B. C. D.
5.如图,某校数学兴趣小组探究活动中要测量河的宽度,该小组同学在河岸一边上选定一点A,再在河岸另一边选定点P和点B,使(河的两岸平行).若利用测量工具测得为m米,,根据测量数据可计算得到小河宽度为( )
A.米 B.米 C.米 D.米
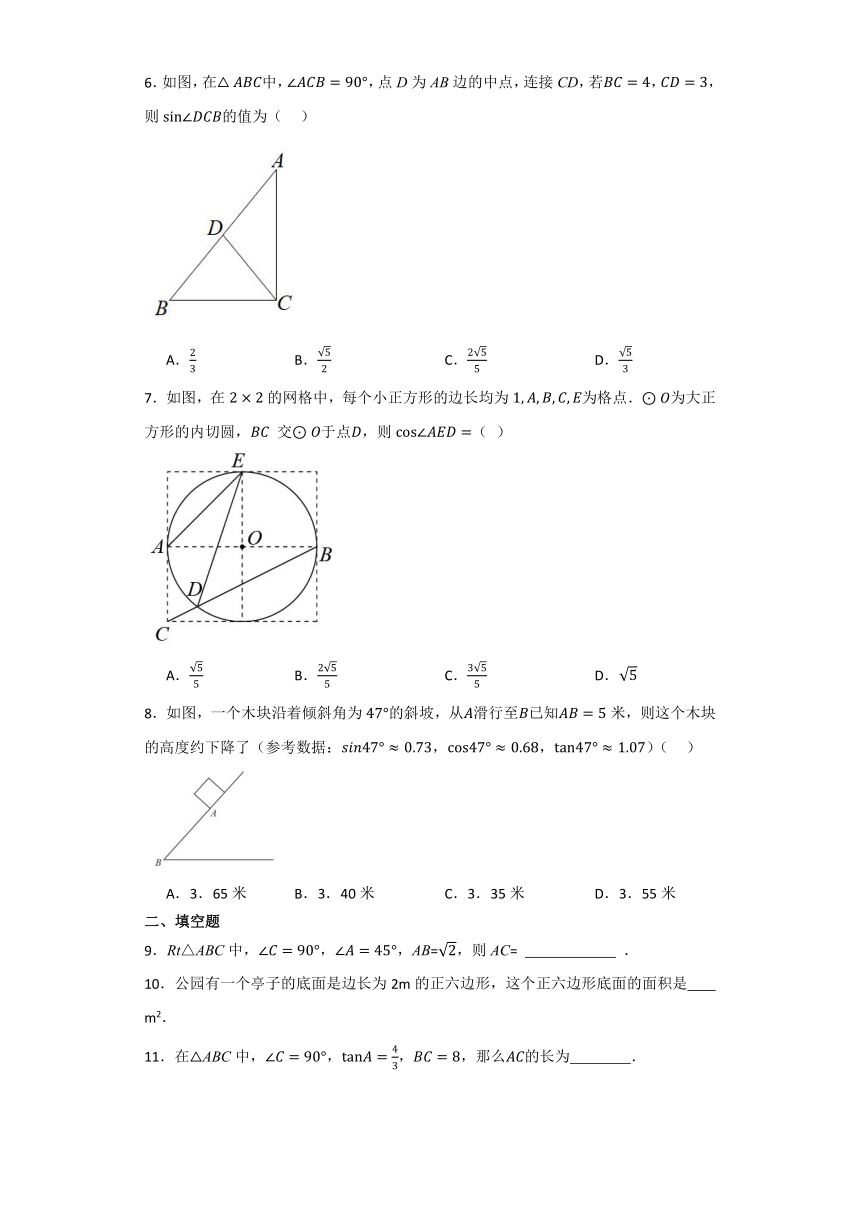
6.如图,在中,,点D为AB边的中点,连接CD,若,,则的值为( )
A. B. C. D.
7.如图,在的网格中,每个小正方形的边长均为为格点.为大正方形的内切圆, 交于点,则( )
A. B. C. D.
8.如图,一个木块沿着倾斜角为的斜坡,从滑行至已知米,则这个木块的高度约下降了(参考数据:,,)( )
A.3.65米 B.3.40米 C.3.35米 D.3.55米
二、填空题
9.Rt△ABC中,,,AB=,则AC= .
10.公园有一个亭子的底面是边长为2m的正六边形,这个正六边形底面的面积是 m2.
11.在ABC中,,,,那么的长为 .
12.如图, ,点P在OA上, PC=PD,若CO=5cm,OD=8cm ,则 OP的长是 .
13.如图,在△ABC中,点D是BC的中点,DA⊥AC,tan∠BAD=,AB=,则BC的长度为 .
14.如图,一段与水平面成30°角的斜坡上有两棵树,两棵树水平距离为,树的高度都是.一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 .
15.如图,中,CD是AB边上的高,AC=8,∠ACD=30°,tan∠ACB=,点P为CD上一动点,当BP+CP最小时,DP= .
16.在⊙O中,半径R=1,弦AB=,弦AC=,则∠BAC的度数为 .
三、解答题
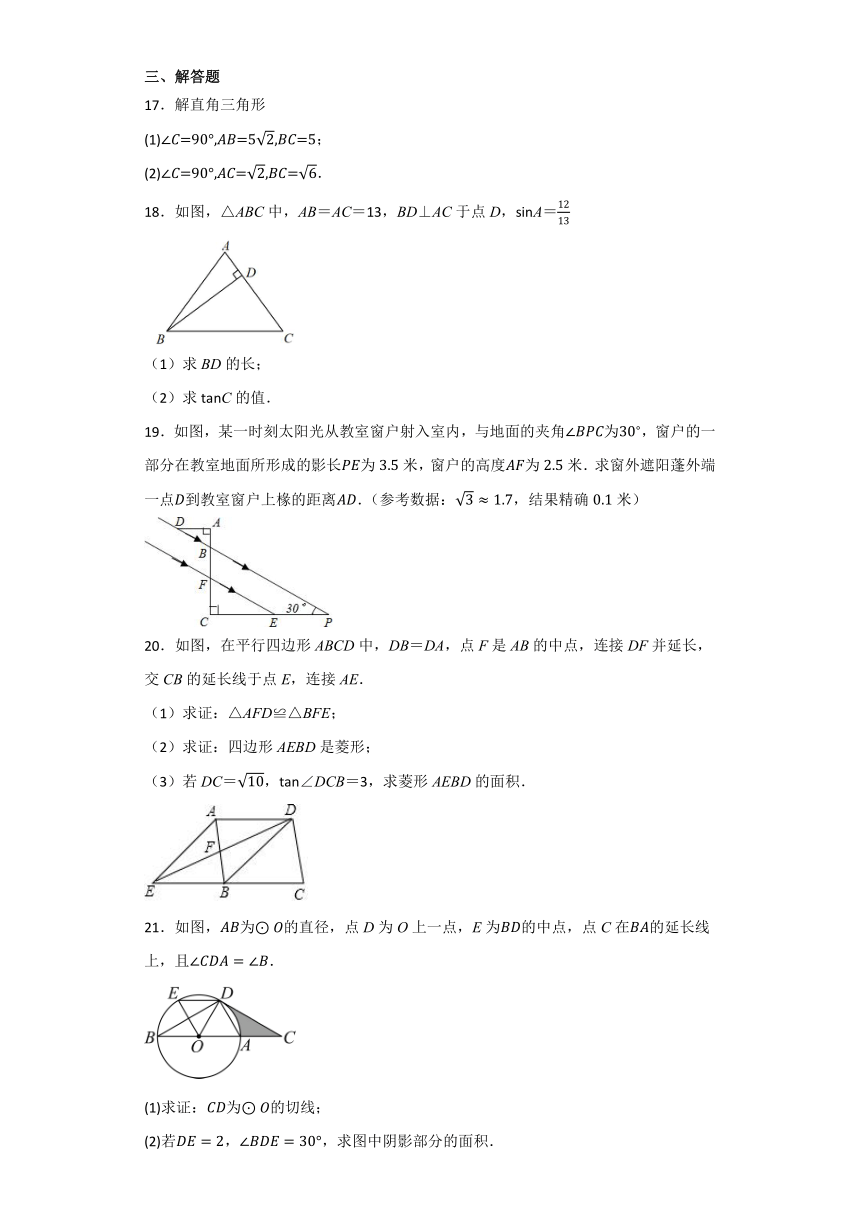
17.解直角三角形
(1);
(2).
18.如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
(1)求BD的长;
(2)求tanC的值.
19.如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角为,窗户的一部分在教室地面所形成的影长为米,窗户的高度为米.求窗外遮阳蓬外端一点到教室窗户上椽的距离.(参考数据:,结果精确米)
20.如图,在平行四边形ABCD中,DB=DA,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE.
(1)求证:△AFD≌△BFE;
(2)求证:四边形AEBD是菱形;
(3)若DC=,tan∠DCB=3,求菱形AEBD的面积.
21.如图,为的直径,点D为O上一点,E为的中点,点C在的延长线上,且.
(1)求证:为的切线;
(2)若,,求图中阴影部分的面积.
22.如图,在中,是上的一点,与交于点,与交于点.
(1)如图1,是的中点.
①求证:.
②求的值.
(2)如图2,若,,,,求的长.
参考答案
1.解:在中,,
∴,
∴,
故选:A.
2.解:在中,
,
.
,
.
.
.
故选:D.
3.解:在中, 的长约为米,约为,,
∴.
故选:A.
4.解:∵四边形是矩形,,,
∴,,
∵对角线的垂直平分线分别交于点,
∴,,
∵,则,
∴,
∴,
解得:,
故选:D
5.解:∵BP⊥AP,
∴∠APB=90°,
在Rt△ABP中,PB=m米,∠PBA=α,
∴PA=PB tanα=mtanα(米),
∴小河宽度PA为mtanα米,
故选:C.
6.解:∵在△ABC中,∠ACB=90°,点D为AB边的中点,
∴AD=BD=CD=AB,
∴,
又∵CD=3,
∴AB=6,
,
∴==,
故选:D.
7.解:由题意可得,∠AED=∠ABD
在Rt△ABC中,AC=1,AB=2,由勾股定理可得:
BC=
所以cos∠AED=cos∠ABD=
故选:B.
8.解:本题考查三角函数的定义.过点作水平面的垂线,垂足为,则,故(米),故选A.
9.解:Rt△ABC中,,
∴,
∴,
故答案为:1.
10.解:如图,连接正六边形对角顶点交于O点,过O点作AB边垂线于H点,
易知为等边三角形,,,
,
这个正六边形底面的面积,
故答案为:.
11.解:∵在ABC中,,,,
∴;
故答案为6.
12.解:过点P作PE⊥OB
∵CO=5cm,OD=8cm ,
∴CD=OD-CO=3
又∵PC=PD,PE⊥OB
∴CE=
∴OE=OC+CE=
∴在Rt△POE中,
故答案为:13cm.
13.解:作DE∥AC交AB于E,如图,
∵DA⊥AC,
∴DE⊥AD,
∴∠ADE=90,
∵点D是BC的中点,
∴DE为△ABC的中位线,
∴DE=AC,AE=BE=AB=2,
在Rt△ADE中,tan∠EAD==,
设DE=x,则AD=2x,
∵AD2+DE2=AE2,
∴(2x)2+x2=(2)2,解得x=2,
∴DE=2,AD=4,
∴AC=2DE=4,
∴CD=,
∴BC=2CD=
故答案为:.
14.解:如图,∵∠BAC=30,∠ACB=90,AC=,
∴AB=AC/cos30=(m).
故答案是:12.
15.解:如图,作PE⊥AC于E,BE′⊥AC于E′交CD于P′.
∵CD⊥AB,∠ACD=30°,∠PEC=90°,AC=8,
∴PE=PC,∠A=60°,∠ABE′=30°,AD=4,CD=4,
∴PB+PC=PB+PE,
∴当BE′⊥AC时,PB+PE=BP′+P′E′=BE′最小,
∵tan∠ACB=,设BE′=5,CE′=3k,
∴AE′=8﹣3k,AB=16﹣6k,BD=16﹣6k﹣4=12﹣6k,
∴BC2=BD2+CD2=BE′2+CE′2,
∴(12﹣6k)2+48=9k2+75k2,
整理得k2+3k﹣4=0,
∴k=1或﹣4(舍弃),
∴BE′=5,
∴PB+PC的最小值为5.
16.解:利用垂径定理可知:AD=,AE=,根据直角三角形中三角函数的值可知:sin∠AOD=,
所以可得∠AOD=60°,由sin∠AOE=,可得∠AOE=45°,因此可求得∠BAC=75°.而当两弦共弧的时候就是15°.
17.(1)解:∵,
∴,,
∴,
∴;
(2)解:,
∴,,
∴,
∴.
18.解:(1)∵△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
∴
即
解得:BD=12;
(2)∵AC=AB=13,BD=12,BD⊥AC,
∴AD=5,
∴DC=8,
∴tan∠C=
19.解:过E作EG∥AC交BP于G,
∵EF∥DP,
∴四边形BFEG是平行四边形.
在Rt△PEG中,PE=3.5m,∠P=30
,
tan∠EPG=,
∴EG=EP tan∠P=3.5×tan30≈2.02(m).
又∵四边形BFEG是平行四边形,
∴BF=EG=2.02m,
∴AB=AF BF=2.5 2.02=0.48(m).
又∵AD∥PE,∠BDA=∠P=30,
在Rt△BAD中,tan30=,
∴AD= =0.48×≈0.8(米).
答:窗外遮阳蓬外端一点D到教室窗户上椽的距离AD为0.8m.
20.解:(1)∵四边形ABCD是平行四边形,
∴AD∥CE,
∴∠DAF=∠EBF,
∵∠AFD=∠EFB,AF=FB,
∴△AFD≌△BFE(AAS);
(2)∵△AFD≌△BFE,
∴AD=EB,∵AD∥EB,
∴四边形AEBD是平行四边形,
∵BD=AD,
∴四边形AEBD是菱形.
(3)∵四边形ABCD是平行四边形,
∴CD=AB=,AB∥CD,
∴∠ABE=∠DCB,
∴tan∠ABE=tan∠DCB=3,
∵四边形AEBD是菱形,
∴AB⊥DE,AF=FB,EF=DF,
∴tan∠ABE==3,
∵BF=,
∴EF=,
∴DE=3,
∴S菱形AEBD= AB DE==15.
21.(1)证明:∵为的直径,
∴,
即,
∵,
∴,
∵,
∴,
∴,
即,
∴,
∵为的半径,
∴为的切线;
(2)解:∵E为的中点,,
∴,
∵,
∴,
∵,
∴为等边三角形,
∴,
∵,
所以
∴,
∴图中阴影部分的面积,
则
所以图中阴影部分的面积为
22.(1)解:①证明:如图1,
∵四边形,
∴
∴,
∴,
∴,
∵点为中点,
∴,
即,
∴;
②连接,
∵平行四边形对角线和相交于点,
∴点是的中点,
∵点为的中点,
∴是的中位线,
∴,
∴,,
∴,
故.
(2)解:∵,
∴平行四边形为菱形,
∴,
∵,
∴,
∵,,
∴,,
∴,
∵,
∴
解得:,
,
,
∴
故
一、单选题
1.在中,,当已知和a时,求c,应选择的关系式是( )
A. B. C. D.
2.在中,,,,则的长为( )
A.3 B.2 C. D.
3.某楼梯的侧面如图所示,已测得的长约为米,约为,则该楼梯的高度可表示为( )
A. B. C. D.
4.如图,在矩形中,,,对角线的垂直平分线分别交于点,则的长为( )
A. B. C. D.
5.如图,某校数学兴趣小组探究活动中要测量河的宽度,该小组同学在河岸一边上选定一点A,再在河岸另一边选定点P和点B,使(河的两岸平行).若利用测量工具测得为m米,,根据测量数据可计算得到小河宽度为( )
A.米 B.米 C.米 D.米
6.如图,在中,,点D为AB边的中点,连接CD,若,,则的值为( )
A. B. C. D.
7.如图,在的网格中,每个小正方形的边长均为为格点.为大正方形的内切圆, 交于点,则( )
A. B. C. D.
8.如图,一个木块沿着倾斜角为的斜坡,从滑行至已知米,则这个木块的高度约下降了(参考数据:,,)( )
A.3.65米 B.3.40米 C.3.35米 D.3.55米
二、填空题
9.Rt△ABC中,,,AB=,则AC= .
10.公园有一个亭子的底面是边长为2m的正六边形,这个正六边形底面的面积是 m2.
11.在ABC中,,,,那么的长为 .
12.如图, ,点P在OA上, PC=PD,若CO=5cm,OD=8cm ,则 OP的长是 .
13.如图,在△ABC中,点D是BC的中点,DA⊥AC,tan∠BAD=,AB=,则BC的长度为 .
14.如图,一段与水平面成30°角的斜坡上有两棵树,两棵树水平距离为,树的高度都是.一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 .
15.如图,中,CD是AB边上的高,AC=8,∠ACD=30°,tan∠ACB=,点P为CD上一动点,当BP+CP最小时,DP= .
16.在⊙O中,半径R=1,弦AB=,弦AC=,则∠BAC的度数为 .
三、解答题
17.解直角三角形
(1);
(2).
18.如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
(1)求BD的长;
(2)求tanC的值.
19.如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角为,窗户的一部分在教室地面所形成的影长为米,窗户的高度为米.求窗外遮阳蓬外端一点到教室窗户上椽的距离.(参考数据:,结果精确米)
20.如图,在平行四边形ABCD中,DB=DA,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE.
(1)求证:△AFD≌△BFE;
(2)求证:四边形AEBD是菱形;
(3)若DC=,tan∠DCB=3,求菱形AEBD的面积.
21.如图,为的直径,点D为O上一点,E为的中点,点C在的延长线上,且.
(1)求证:为的切线;
(2)若,,求图中阴影部分的面积.
22.如图,在中,是上的一点,与交于点,与交于点.
(1)如图1,是的中点.
①求证:.
②求的值.
(2)如图2,若,,,,求的长.
参考答案
1.解:在中,,
∴,
∴,
故选:A.
2.解:在中,
,
.
,
.
.
.
故选:D.
3.解:在中, 的长约为米,约为,,
∴.
故选:A.
4.解:∵四边形是矩形,,,
∴,,
∵对角线的垂直平分线分别交于点,
∴,,
∵,则,
∴,
∴,
解得:,
故选:D
5.解:∵BP⊥AP,
∴∠APB=90°,
在Rt△ABP中,PB=m米,∠PBA=α,
∴PA=PB tanα=mtanα(米),
∴小河宽度PA为mtanα米,
故选:C.
6.解:∵在△ABC中,∠ACB=90°,点D为AB边的中点,
∴AD=BD=CD=AB,
∴,
又∵CD=3,
∴AB=6,
,
∴==,
故选:D.
7.解:由题意可得,∠AED=∠ABD
在Rt△ABC中,AC=1,AB=2,由勾股定理可得:
BC=
所以cos∠AED=cos∠ABD=
故选:B.
8.解:本题考查三角函数的定义.过点作水平面的垂线,垂足为,则,故(米),故选A.
9.解:Rt△ABC中,,
∴,
∴,
故答案为:1.
10.解:如图,连接正六边形对角顶点交于O点,过O点作AB边垂线于H点,
易知为等边三角形,,,
,
这个正六边形底面的面积,
故答案为:.
11.解:∵在ABC中,,,,
∴;
故答案为6.
12.解:过点P作PE⊥OB
∵CO=5cm,OD=8cm ,
∴CD=OD-CO=3
又∵PC=PD,PE⊥OB
∴CE=
∴OE=OC+CE=
∴在Rt△POE中,
故答案为:13cm.
13.解:作DE∥AC交AB于E,如图,
∵DA⊥AC,
∴DE⊥AD,
∴∠ADE=90,
∵点D是BC的中点,
∴DE为△ABC的中位线,
∴DE=AC,AE=BE=AB=2,
在Rt△ADE中,tan∠EAD==,
设DE=x,则AD=2x,
∵AD2+DE2=AE2,
∴(2x)2+x2=(2)2,解得x=2,
∴DE=2,AD=4,
∴AC=2DE=4,
∴CD=,
∴BC=2CD=
故答案为:.
14.解:如图,∵∠BAC=30,∠ACB=90,AC=,
∴AB=AC/cos30=(m).
故答案是:12.
15.解:如图,作PE⊥AC于E,BE′⊥AC于E′交CD于P′.
∵CD⊥AB,∠ACD=30°,∠PEC=90°,AC=8,
∴PE=PC,∠A=60°,∠ABE′=30°,AD=4,CD=4,
∴PB+PC=PB+PE,
∴当BE′⊥AC时,PB+PE=BP′+P′E′=BE′最小,
∵tan∠ACB=,设BE′=5,CE′=3k,
∴AE′=8﹣3k,AB=16﹣6k,BD=16﹣6k﹣4=12﹣6k,
∴BC2=BD2+CD2=BE′2+CE′2,
∴(12﹣6k)2+48=9k2+75k2,
整理得k2+3k﹣4=0,
∴k=1或﹣4(舍弃),
∴BE′=5,
∴PB+PC的最小值为5.
16.解:利用垂径定理可知:AD=,AE=,根据直角三角形中三角函数的值可知:sin∠AOD=,
所以可得∠AOD=60°,由sin∠AOE=,可得∠AOE=45°,因此可求得∠BAC=75°.而当两弦共弧的时候就是15°.
17.(1)解:∵,
∴,,
∴,
∴;
(2)解:,
∴,,
∴,
∴.
18.解:(1)∵△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
∴
即
解得:BD=12;
(2)∵AC=AB=13,BD=12,BD⊥AC,
∴AD=5,
∴DC=8,
∴tan∠C=
19.解:过E作EG∥AC交BP于G,
∵EF∥DP,
∴四边形BFEG是平行四边形.
在Rt△PEG中,PE=3.5m,∠P=30
,
tan∠EPG=,
∴EG=EP tan∠P=3.5×tan30≈2.02(m).
又∵四边形BFEG是平行四边形,
∴BF=EG=2.02m,
∴AB=AF BF=2.5 2.02=0.48(m).
又∵AD∥PE,∠BDA=∠P=30,
在Rt△BAD中,tan30=,
∴AD= =0.48×≈0.8(米).
答:窗外遮阳蓬外端一点D到教室窗户上椽的距离AD为0.8m.
20.解:(1)∵四边形ABCD是平行四边形,
∴AD∥CE,
∴∠DAF=∠EBF,
∵∠AFD=∠EFB,AF=FB,
∴△AFD≌△BFE(AAS);
(2)∵△AFD≌△BFE,
∴AD=EB,∵AD∥EB,
∴四边形AEBD是平行四边形,
∵BD=AD,
∴四边形AEBD是菱形.
(3)∵四边形ABCD是平行四边形,
∴CD=AB=,AB∥CD,
∴∠ABE=∠DCB,
∴tan∠ABE=tan∠DCB=3,
∵四边形AEBD是菱形,
∴AB⊥DE,AF=FB,EF=DF,
∴tan∠ABE==3,
∵BF=,
∴EF=,
∴DE=3,
∴S菱形AEBD= AB DE==15.
21.(1)证明:∵为的直径,
∴,
即,
∵,
∴,
∵,
∴,
∴,
即,
∴,
∵为的半径,
∴为的切线;
(2)解:∵E为的中点,,
∴,
∵,
∴,
∵,
∴为等边三角形,
∴,
∵,
所以
∴,
∴图中阴影部分的面积,
则
所以图中阴影部分的面积为
22.(1)解:①证明:如图1,
∵四边形,
∴
∴,
∴,
∴,
∵点为中点,
∴,
即,
∴;
②连接,
∵平行四边形对角线和相交于点,
∴点是的中点,
∵点为的中点,
∴是的中位线,
∴,
∴,,
∴,
故.
(2)解:∵,
∴平行四边形为菱形,
∴,
∵,
∴,
∵,,
∴,,
∴,
∵,
∴
解得:,
,
,
∴
故
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
