2023—2024学年人教版九年级数学下册第28章锐角三角函数单元综合测试题(含解析)
文档属性
| 名称 | 2023—2024学年人教版九年级数学下册第28章锐角三角函数单元综合测试题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 718.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 00:00:00 | ||
图片预览

文档简介
2023-2024学年人教版九年级数学下册《第28章锐角三角函数》单元综合测试题(附答案)
一.选择题(满分32分)
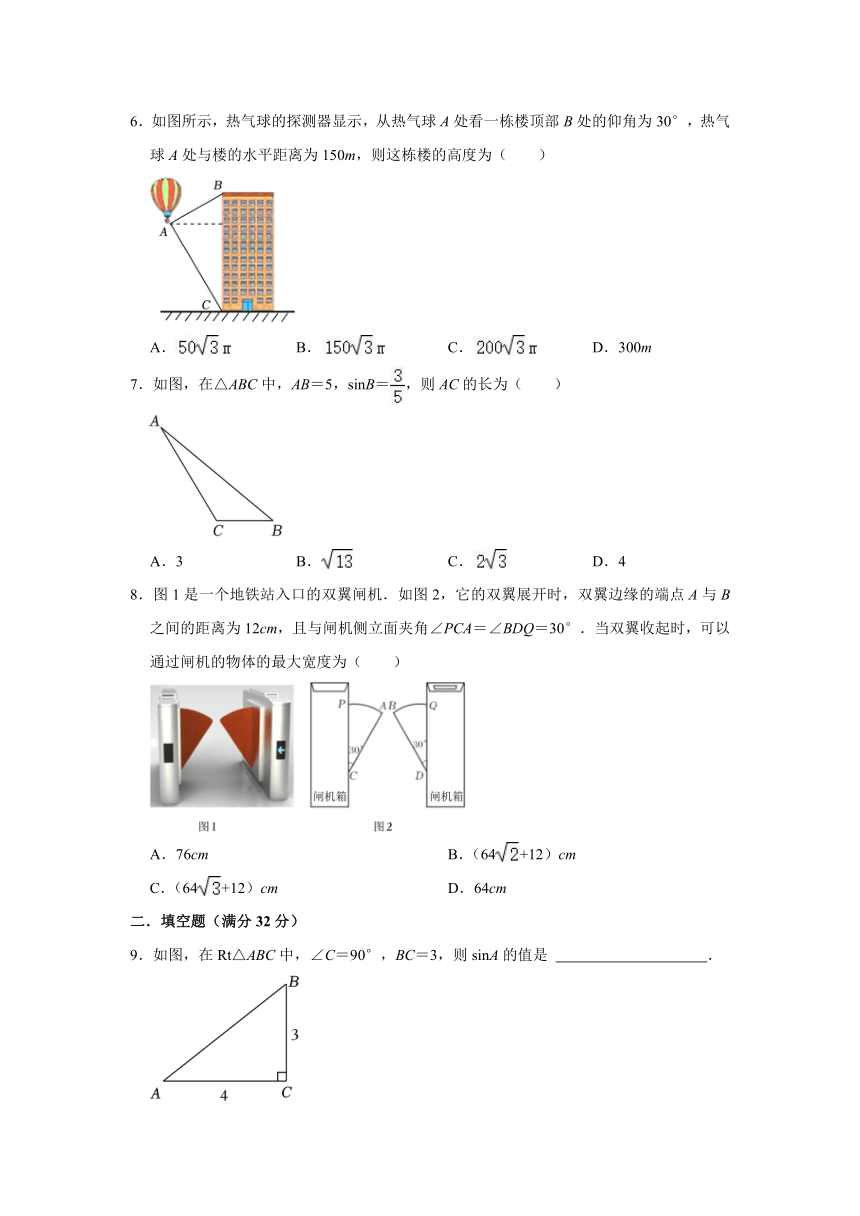
1.Rt△ABC中,∠C=90°,sinA=,则AC的长为( )
A.6 B.8 C.10 D.12
2.如图,在△ABC中,∠ACB=90°,BC=3,CD是△ABC的高( )
A. B. C. D.
3.如图,在6×4网格正方形中,每个小正方形的边长为1,若△ABC的顶点均是格点,则sin∠ABC的值是( )
A. B. C. D.
4.在山坡上植树,要求两棵树间的坡面距离是3,测得斜坡的倾斜角为27°( )
A.3sin27° B.3cos27° C. D.3tan27°
5.如图,小明在地面C处测得建筑物顶点A的仰角为30°,在地面D处测得建筑物顶点A的仰角为45°,D,C在一条直线上,已知CD=26米( )
A.(13+13)米 B.(13+13)米
C.26米 D.26米
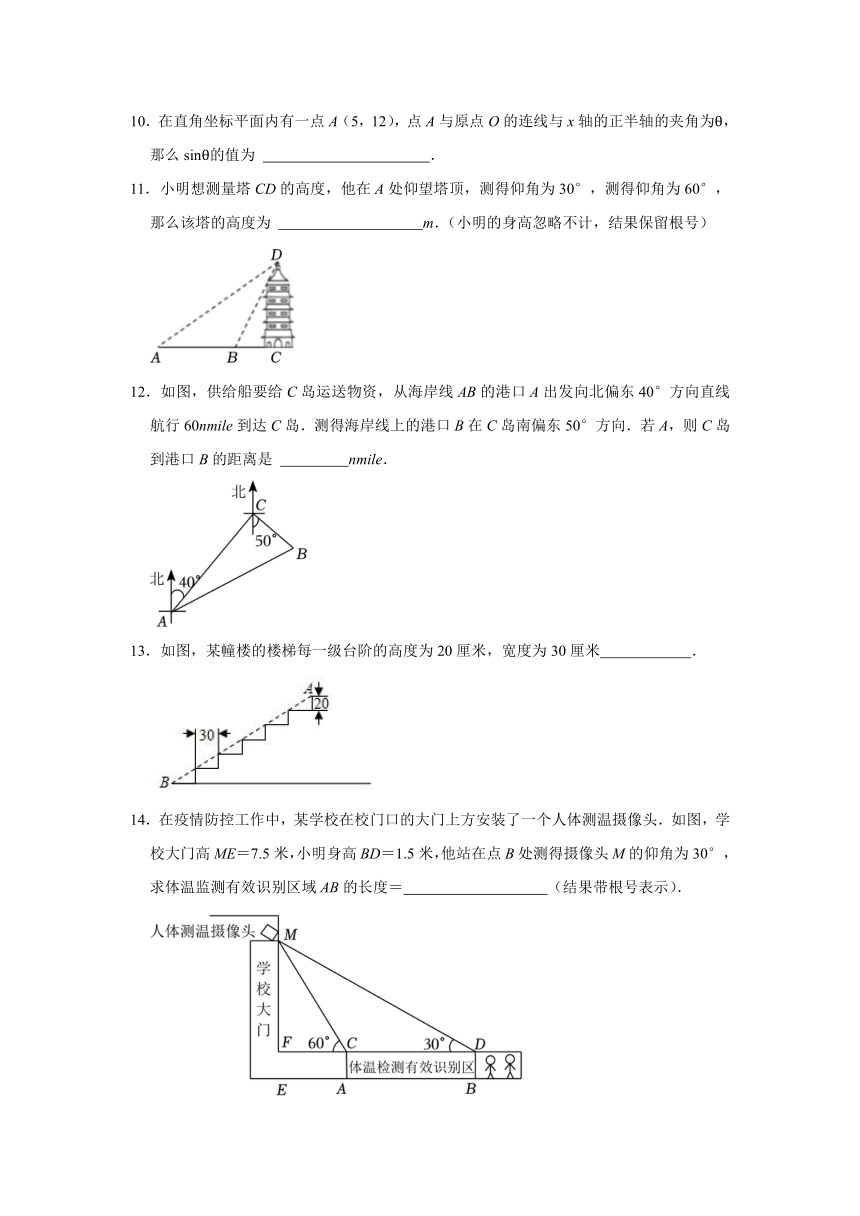
6.如图所示,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,热气球A处与楼的水平距离为150m,则这栋楼的高度为( )
A. B. C. D.300m
7.如图,在△ABC中,AB=5,sinB=,则AC的长为( )
A.3 B. C. D.4
8.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为12cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A.76cm B.(64+12)cm
C.(64+12)cm D.64cm
二.填空题(满分32分)
9.如图,在Rt△ABC中,∠C=90°,BC=3,则sinA的值是 .
10.在直角坐标平面内有一点A(5,12),点A与原点O的连线与x轴的正半轴的夹角为θ,那么sinθ的值为 .
11.小明想测量塔CD的高度,他在A处仰望塔顶,测得仰角为30°,测得仰角为60°,那么该塔的高度为 m.(小明的身高忽略不计,结果保留根号)
12.如图,供给船要给C岛运送物资,从海岸线AB的港口A出发向北偏东40°方向直线航行60nmile到达C岛.测得海岸线上的港口B在C岛南偏东50°方向.若A,则C岛到港口B的距离是 nmile.
13.如图,某幢楼的楼梯每一级台阶的高度为20厘米,宽度为30厘米 .
14.在疫情防控工作中,某学校在校门口的大门上方安装了一个人体测温摄像头.如图,学校大门高ME=7.5米,小明身高BD=1.5米,他站在点B处测得摄像头M的仰角为30°,求体温监测有效识别区域AB的长度= (结果带根号表示).
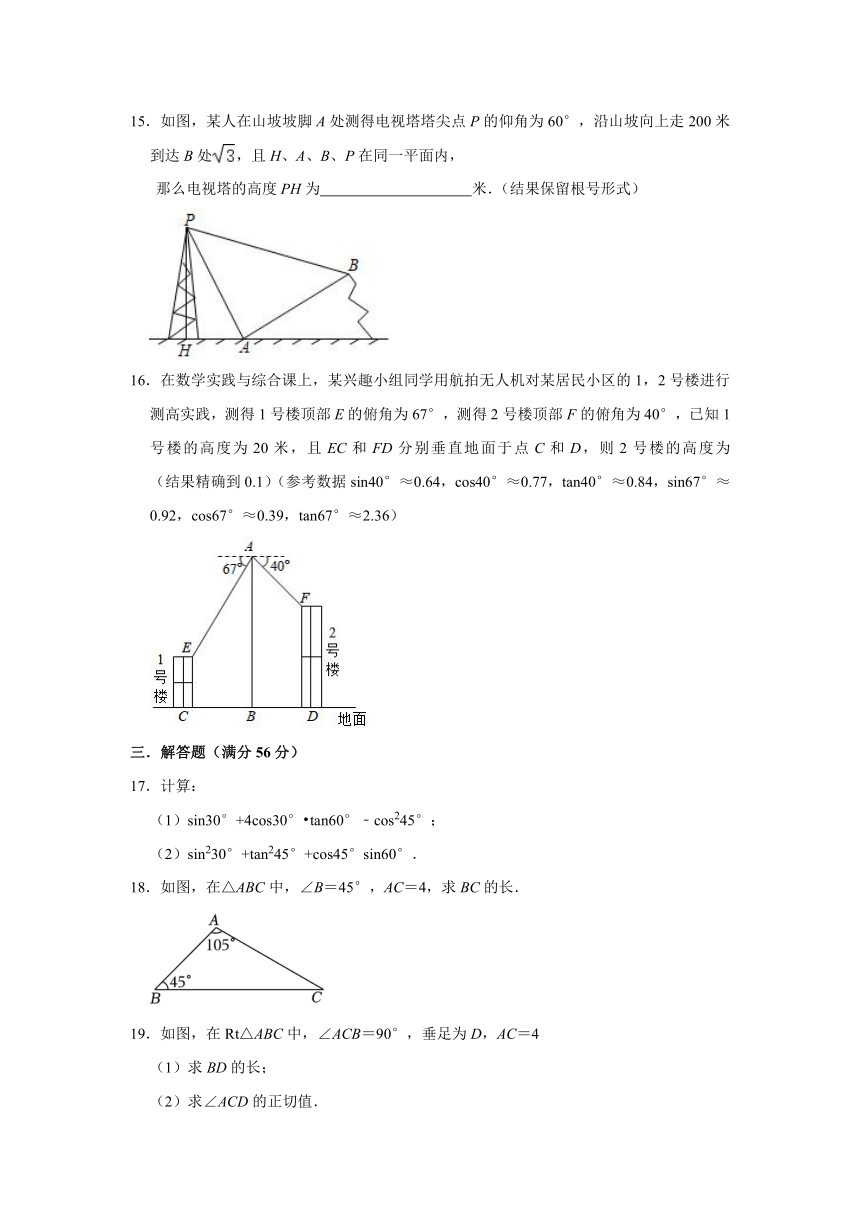
如图,某人在山坡坡脚A处测得电视塔塔尖点P的仰角为60°,沿山坡向上走200米到达B处,且H、A、B、P在同一平面内,
那么电视塔的高度PH为 米.(结果保留根号形式)
16.在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1,2号楼进行测高实践,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D,则2号楼的高度为 (结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
三.解答题(满分56分)
17.计算:
(1)sin30°+4cos30° tan60°﹣cos245°;
(2)sin230°+tan245°+cos45°sin60°.
18.如图,在△ABC中,∠B=45°,AC=4,求BC的长.
19.如图,在Rt△ABC中,∠ACB=90°,垂足为D,AC=4
(1)求BD的长;
(2)求∠ACD的正切值.
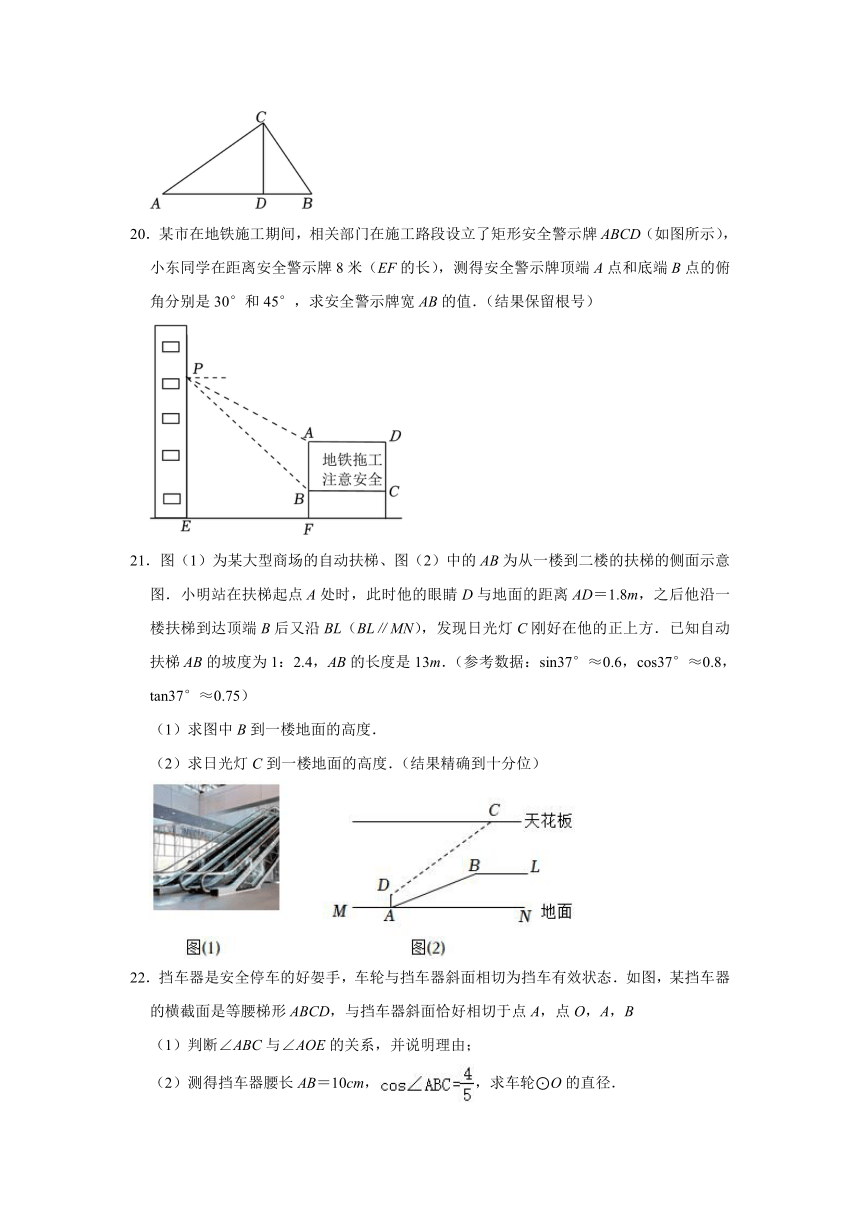
20.某市在地铁施工期间,相关部门在施工路段设立了矩形安全警示牌ABCD(如图所示),小东同学在距离安全警示牌8米(EF的长),测得安全警示牌顶端A点和底端B点的俯角分别是30°和45°,求安全警示牌宽AB的值.(结果保留根号)
21.图(1)为某大型商场的自动扶梯、图(2)中的AB为从一楼到二楼的扶梯的侧面示意图.小明站在扶梯起点A处时,此时他的眼睛D与地面的距离AD=1.8m,之后他沿一楼扶梯到达顶端B后又沿BL(BL∥MN),发现日光灯C刚好在他的正上方.已知自动扶梯AB的坡度为1:2.4,AB的长度是13m.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
(1)求图中B到一楼地面的高度.
(2)求日光灯C到一楼地面的高度.(结果精确到十分位)
22.挡车器是安全停车的好妿手,车轮与挡车器斜面相切为挡车有效状态.如图,某挡车器的横截面是等腰梯形ABCD,与挡车器斜面恰好相切于点A,点O,A,B
(1)判断∠ABC与∠AOE的关系,并说明理由;
(2)测得挡车器腰长AB=10cm,,求车轮⊙O的直径.
参考答案
一.选择题(满分32分)
1.解:∵在Rt△ABC中,∠C=90°,
∴sinA=,
∵AB=10,
∴BC=8,
∴AC==8,
故选:B.
2.解:∵∠ACB=90°,
∴∠BCD+∠ACD=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠DCA+∠A=90°,
∴∠BCD=∠A,
在Rt△ABC中,tanA==,
∴tan∠BCD=tanA=,
故选:D.
3.解:
∵△ABD是直角三角形,
∴AB===2,
∴sin∠ABC===,
故选:A.
4.解:如图,过点A作AB⊥BC于B,
∴∠ABC=90°,cos∠BAC=,
∵AC=3,∠BAC=27°,
∴AB=ACcos∠BAC=3cos27°;
故选:B.
5.解:设AB=x米,
在Rt△ABD中,∠ADB=45°,
∴DB==x(米),
在Rt△ABC中,∠C=30°,
∴BC===x(米),
∵BC﹣BD=CD,
∴x﹣x=26,
∴x=13+13,
∴AB=(13+13)米,
∴该建筑物AB的高度为(13+13)米,
故选:B.
6.解:过点A作AD⊥BC于点D,则∠BAD=30°,AD=150m,
在Rt△ABD中,BD=AD tan30°=150×(m),
在Rt△ACD中,CD=AD tan60°=150×(m),
∴BC=BD+CD=200(m).
故选:C.
7.解:过A作AH⊥BC,交BC延长线于H,
∵sinB==,AB=7,
∴AH=3,
∴BH==4,
∴HC=BH﹣BC=4﹣8=2,
∴AC==.
故选:B.
8.解:如图所示,过A作AE⊥CP于E,
则Rt△ACE中,AE=×64=32(cm),
同理可得,BF=32cm,
又∵点A与B之间的距离为12cm,
∴通过闸机的物体的最大宽度为32+12+32=76(cm),
故选:A.
二.填空题(满分32分)
9.解:在Rt△ABC中,∠C=90°,BC=3,
则,
∴,
故答案为:.
10.解:如图,过A作AH⊥x轴于H,
∴AH=12,OH=5,
∴OA===13,
∴sinθ==.
故答案为:.
11.解:∵∠DAB=30°,∠DBC=60°,
∴BD=AB=50m.
∴DC=BD sin60°=50×=25,
答:该塔高25m,
故答案为:25.
12.解:如图,过点A作AD⊥CD于点D,
根据题意得:∠CAD=90°﹣40°=50°,
∴∠ACD=90°﹣∠CAD=40°,
∴∠ACB=40°+50°=90°,
∵AC=60nmile,AB=65nmile,
∴BC==25(nmile).
故答案为:25.
13.解:斜面AB的坡度为20:30=1:1.6,
故答案为:1:1.4.
14.解:根据题意可知:四边形EFCA和ABDC是矩形,ME=7.5米,
∴CA=EF=BD=3.5米,CD=AB,
设FC=x,
在Rt△MFC中,
∵∠MCF=60°,
∴∠FMC=30°,
∴MC=2FC=3x,MF=x,
∵∠MDC=30°,
∴∠CMD=60°﹣30°=30°,
∴CD=CM=2x,
∵ME=MF+EF,
∴x+1.5=7.5,
解得:x=2,
∴MC=2x=4(米),
答:体温监测有效识别区域AB的长为4米,
故答案为:3米.
15.解:过B作BM⊥HA于M,过B作BN∥AM
则∠AMB=90°,∠ABN=∠BAM,
由题意得:AB=200米,∠PBN=15°,
∵山坡AB的坡度i=1:,
∴tan∠BAM=6:=,
∴∠BAM=30°,
∴∠ABN=30°,
∴∠PAB=180°﹣∠PAH﹣∠BAM=90°,∠ABP=∠ABN+∠PBN=45°,
∴△PAB是等腰直角三角形,
∴PA=AB=200米,
在Rt△PAH中,sin∠PAH=,
∴PH=PA=100,
故答案为:100.
16.解:过点E、F分别作EM⊥AB,垂足分别为M、N,
由题意得,EC=20,∠AFN=40°,AB=60,
∴AM=AB﹣MB=60﹣20=40,
在Rt△AEM中,
∵tan∠AEM=,
∴EM==≈16.9,
在Rt△AFN中,
∵tan∠AFN=,
∴AN=tan40°×16.9≈14.4,
∴FD=NB=AB﹣AN=60﹣14.2=45.8,
答:8号楼的高度约为45.8米,
故答案为:45.8米.
三.解答题(满分56分)
17.解:(1)原式===7;
(2)原式===.
18.解:如图所示,过点A作AD⊥BC于D,
∵在△ABC中,∠B=45°,
∴∠C=180°﹣∠B﹣∠BAC=30°,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠BAD=45°=∠B,
∴AD=BD,
∵AC=4,
∴,
∴,
∴.
19.解:(1)在Rt△ABC中,∠ACB=90°,BC=3,
∴AB==5,
∵CD⊥AB,
∵S△ABC=AB CD=,
∴CD===.
∵tanB==,
∴=,
∴BD=;
(2)∵AB=7,BD=,
∴AD=AB﹣BD=,
∵CD⊥AB,
∴tan∠ACD===.
20.解:如图:延长BA交PH于点G,
由题意得:
EF=PG=8米,∠PGA=90°,
在Rt△PAG中,∠GPA=30°,
∴AG=PG tan30°=8×=(米),
在Rt△PGB中,∠GPB=45°,
∴GB=PG tan45°=8×3=8(米),
∴AB=GB﹣GA=(8﹣)米,
∴安全警示牌宽AB的值为(5﹣)米.
21.解:(1)过点B作BE⊥MN于E,如图(2)所示:
设AE=xm,
∵AB的坡度为1:2.2,
∴=,
∴BE=xm,
在Rt△ABE中,由勾股定理得:x2+(x)2=132,
解得:x=12,
∴AE=12m,BE=5m,
答:B到一楼地面的高度为5m;
(2)过点C作CF⊥MN于F交BL于G,过点D作DJ⊥CF于J交BE于H,
则BG=2m,四边形BEFG,∠CDJ=37°,
∴EF=BG=4m,AD=FJ=1.8m,
由(1)可知,AF=AE+EF=12+4=14(m),
∴DJ=14m,
在Rt△CDJ中,tan∠CDJ=,
∴CJ≈0.75DJ=0.75×14=10.4(m),
∴CF=CJ+FJ=10.5+1.2=12.3(m),
答:日光灯C到一楼地面的高度约为12.3m.
22.解:(1)∠ABC=∠AOE.
理由如下:
由题意可知,⊙O与CB相切于点E,
∴∠OAB=90°,∠OEB=90°,
∵∠ABE+∠AOE+∠OAB+∠OEB=360°,
∴∠ABE+∠AOE=180°.
∵∠ABC+∠ABE=180°,
∴∠ABC=∠AOE;
(2)过点A作AH⊥BC于点H,AF⊥OE于点F,
在Rt△ABH中,∵AB=10,,
∴HB=AB cos∠ABC=2,
∵BA,BE分别与⊙O相切于A,E,
∴BE=AB=10,
∵AH⊥BC,AF⊥OE,
∴∠AHE=∠AFE=∠FEH=90°,
∴四边形AHEF是矩形,
∴AF=HE=HB+BE=18,
∵∠ABC=∠AOE,,
∴.
在Rt△OAF中,.
∵OA2﹣OF2=AF2,
∴,
解得:OA=30,
∴车轮⊙O的直径是60cm.
一.选择题(满分32分)
1.Rt△ABC中,∠C=90°,sinA=,则AC的长为( )
A.6 B.8 C.10 D.12
2.如图,在△ABC中,∠ACB=90°,BC=3,CD是△ABC的高( )
A. B. C. D.
3.如图,在6×4网格正方形中,每个小正方形的边长为1,若△ABC的顶点均是格点,则sin∠ABC的值是( )
A. B. C. D.
4.在山坡上植树,要求两棵树间的坡面距离是3,测得斜坡的倾斜角为27°( )
A.3sin27° B.3cos27° C. D.3tan27°
5.如图,小明在地面C处测得建筑物顶点A的仰角为30°,在地面D处测得建筑物顶点A的仰角为45°,D,C在一条直线上,已知CD=26米( )
A.(13+13)米 B.(13+13)米
C.26米 D.26米
6.如图所示,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,热气球A处与楼的水平距离为150m,则这栋楼的高度为( )
A. B. C. D.300m
7.如图,在△ABC中,AB=5,sinB=,则AC的长为( )
A.3 B. C. D.4
8.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为12cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A.76cm B.(64+12)cm
C.(64+12)cm D.64cm
二.填空题(满分32分)
9.如图,在Rt△ABC中,∠C=90°,BC=3,则sinA的值是 .
10.在直角坐标平面内有一点A(5,12),点A与原点O的连线与x轴的正半轴的夹角为θ,那么sinθ的值为 .
11.小明想测量塔CD的高度,他在A处仰望塔顶,测得仰角为30°,测得仰角为60°,那么该塔的高度为 m.(小明的身高忽略不计,结果保留根号)
12.如图,供给船要给C岛运送物资,从海岸线AB的港口A出发向北偏东40°方向直线航行60nmile到达C岛.测得海岸线上的港口B在C岛南偏东50°方向.若A,则C岛到港口B的距离是 nmile.
13.如图,某幢楼的楼梯每一级台阶的高度为20厘米,宽度为30厘米 .
14.在疫情防控工作中,某学校在校门口的大门上方安装了一个人体测温摄像头.如图,学校大门高ME=7.5米,小明身高BD=1.5米,他站在点B处测得摄像头M的仰角为30°,求体温监测有效识别区域AB的长度= (结果带根号表示).
如图,某人在山坡坡脚A处测得电视塔塔尖点P的仰角为60°,沿山坡向上走200米到达B处,且H、A、B、P在同一平面内,
那么电视塔的高度PH为 米.(结果保留根号形式)
16.在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1,2号楼进行测高实践,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D,则2号楼的高度为 (结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
三.解答题(满分56分)
17.计算:
(1)sin30°+4cos30° tan60°﹣cos245°;
(2)sin230°+tan245°+cos45°sin60°.
18.如图,在△ABC中,∠B=45°,AC=4,求BC的长.
19.如图,在Rt△ABC中,∠ACB=90°,垂足为D,AC=4
(1)求BD的长;
(2)求∠ACD的正切值.
20.某市在地铁施工期间,相关部门在施工路段设立了矩形安全警示牌ABCD(如图所示),小东同学在距离安全警示牌8米(EF的长),测得安全警示牌顶端A点和底端B点的俯角分别是30°和45°,求安全警示牌宽AB的值.(结果保留根号)
21.图(1)为某大型商场的自动扶梯、图(2)中的AB为从一楼到二楼的扶梯的侧面示意图.小明站在扶梯起点A处时,此时他的眼睛D与地面的距离AD=1.8m,之后他沿一楼扶梯到达顶端B后又沿BL(BL∥MN),发现日光灯C刚好在他的正上方.已知自动扶梯AB的坡度为1:2.4,AB的长度是13m.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
(1)求图中B到一楼地面的高度.
(2)求日光灯C到一楼地面的高度.(结果精确到十分位)
22.挡车器是安全停车的好妿手,车轮与挡车器斜面相切为挡车有效状态.如图,某挡车器的横截面是等腰梯形ABCD,与挡车器斜面恰好相切于点A,点O,A,B
(1)判断∠ABC与∠AOE的关系,并说明理由;
(2)测得挡车器腰长AB=10cm,,求车轮⊙O的直径.
参考答案
一.选择题(满分32分)
1.解:∵在Rt△ABC中,∠C=90°,
∴sinA=,
∵AB=10,
∴BC=8,
∴AC==8,
故选:B.
2.解:∵∠ACB=90°,
∴∠BCD+∠ACD=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠DCA+∠A=90°,
∴∠BCD=∠A,
在Rt△ABC中,tanA==,
∴tan∠BCD=tanA=,
故选:D.
3.解:
∵△ABD是直角三角形,
∴AB===2,
∴sin∠ABC===,
故选:A.
4.解:如图,过点A作AB⊥BC于B,
∴∠ABC=90°,cos∠BAC=,
∵AC=3,∠BAC=27°,
∴AB=ACcos∠BAC=3cos27°;
故选:B.
5.解:设AB=x米,
在Rt△ABD中,∠ADB=45°,
∴DB==x(米),
在Rt△ABC中,∠C=30°,
∴BC===x(米),
∵BC﹣BD=CD,
∴x﹣x=26,
∴x=13+13,
∴AB=(13+13)米,
∴该建筑物AB的高度为(13+13)米,
故选:B.
6.解:过点A作AD⊥BC于点D,则∠BAD=30°,AD=150m,
在Rt△ABD中,BD=AD tan30°=150×(m),
在Rt△ACD中,CD=AD tan60°=150×(m),
∴BC=BD+CD=200(m).
故选:C.
7.解:过A作AH⊥BC,交BC延长线于H,
∵sinB==,AB=7,
∴AH=3,
∴BH==4,
∴HC=BH﹣BC=4﹣8=2,
∴AC==.
故选:B.
8.解:如图所示,过A作AE⊥CP于E,
则Rt△ACE中,AE=×64=32(cm),
同理可得,BF=32cm,
又∵点A与B之间的距离为12cm,
∴通过闸机的物体的最大宽度为32+12+32=76(cm),
故选:A.
二.填空题(满分32分)
9.解:在Rt△ABC中,∠C=90°,BC=3,
则,
∴,
故答案为:.
10.解:如图,过A作AH⊥x轴于H,
∴AH=12,OH=5,
∴OA===13,
∴sinθ==.
故答案为:.
11.解:∵∠DAB=30°,∠DBC=60°,
∴BD=AB=50m.
∴DC=BD sin60°=50×=25,
答:该塔高25m,
故答案为:25.
12.解:如图,过点A作AD⊥CD于点D,
根据题意得:∠CAD=90°﹣40°=50°,
∴∠ACD=90°﹣∠CAD=40°,
∴∠ACB=40°+50°=90°,
∵AC=60nmile,AB=65nmile,
∴BC==25(nmile).
故答案为:25.
13.解:斜面AB的坡度为20:30=1:1.6,
故答案为:1:1.4.
14.解:根据题意可知:四边形EFCA和ABDC是矩形,ME=7.5米,
∴CA=EF=BD=3.5米,CD=AB,
设FC=x,
在Rt△MFC中,
∵∠MCF=60°,
∴∠FMC=30°,
∴MC=2FC=3x,MF=x,
∵∠MDC=30°,
∴∠CMD=60°﹣30°=30°,
∴CD=CM=2x,
∵ME=MF+EF,
∴x+1.5=7.5,
解得:x=2,
∴MC=2x=4(米),
答:体温监测有效识别区域AB的长为4米,
故答案为:3米.
15.解:过B作BM⊥HA于M,过B作BN∥AM
则∠AMB=90°,∠ABN=∠BAM,
由题意得:AB=200米,∠PBN=15°,
∵山坡AB的坡度i=1:,
∴tan∠BAM=6:=,
∴∠BAM=30°,
∴∠ABN=30°,
∴∠PAB=180°﹣∠PAH﹣∠BAM=90°,∠ABP=∠ABN+∠PBN=45°,
∴△PAB是等腰直角三角形,
∴PA=AB=200米,
在Rt△PAH中,sin∠PAH=,
∴PH=PA=100,
故答案为:100.
16.解:过点E、F分别作EM⊥AB,垂足分别为M、N,
由题意得,EC=20,∠AFN=40°,AB=60,
∴AM=AB﹣MB=60﹣20=40,
在Rt△AEM中,
∵tan∠AEM=,
∴EM==≈16.9,
在Rt△AFN中,
∵tan∠AFN=,
∴AN=tan40°×16.9≈14.4,
∴FD=NB=AB﹣AN=60﹣14.2=45.8,
答:8号楼的高度约为45.8米,
故答案为:45.8米.
三.解答题(满分56分)
17.解:(1)原式===7;
(2)原式===.
18.解:如图所示,过点A作AD⊥BC于D,
∵在△ABC中,∠B=45°,
∴∠C=180°﹣∠B﹣∠BAC=30°,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠BAD=45°=∠B,
∴AD=BD,
∵AC=4,
∴,
∴,
∴.
19.解:(1)在Rt△ABC中,∠ACB=90°,BC=3,
∴AB==5,
∵CD⊥AB,
∵S△ABC=AB CD=,
∴CD===.
∵tanB==,
∴=,
∴BD=;
(2)∵AB=7,BD=,
∴AD=AB﹣BD=,
∵CD⊥AB,
∴tan∠ACD===.
20.解:如图:延长BA交PH于点G,
由题意得:
EF=PG=8米,∠PGA=90°,
在Rt△PAG中,∠GPA=30°,
∴AG=PG tan30°=8×=(米),
在Rt△PGB中,∠GPB=45°,
∴GB=PG tan45°=8×3=8(米),
∴AB=GB﹣GA=(8﹣)米,
∴安全警示牌宽AB的值为(5﹣)米.
21.解:(1)过点B作BE⊥MN于E,如图(2)所示:
设AE=xm,
∵AB的坡度为1:2.2,
∴=,
∴BE=xm,
在Rt△ABE中,由勾股定理得:x2+(x)2=132,
解得:x=12,
∴AE=12m,BE=5m,
答:B到一楼地面的高度为5m;
(2)过点C作CF⊥MN于F交BL于G,过点D作DJ⊥CF于J交BE于H,
则BG=2m,四边形BEFG,∠CDJ=37°,
∴EF=BG=4m,AD=FJ=1.8m,
由(1)可知,AF=AE+EF=12+4=14(m),
∴DJ=14m,
在Rt△CDJ中,tan∠CDJ=,
∴CJ≈0.75DJ=0.75×14=10.4(m),
∴CF=CJ+FJ=10.5+1.2=12.3(m),
答:日光灯C到一楼地面的高度约为12.3m.
22.解:(1)∠ABC=∠AOE.
理由如下:
由题意可知,⊙O与CB相切于点E,
∴∠OAB=90°,∠OEB=90°,
∵∠ABE+∠AOE+∠OAB+∠OEB=360°,
∴∠ABE+∠AOE=180°.
∵∠ABC+∠ABE=180°,
∴∠ABC=∠AOE;
(2)过点A作AH⊥BC于点H,AF⊥OE于点F,
在Rt△ABH中,∵AB=10,,
∴HB=AB cos∠ABC=2,
∵BA,BE分别与⊙O相切于A,E,
∴BE=AB=10,
∵AH⊥BC,AF⊥OE,
∴∠AHE=∠AFE=∠FEH=90°,
∴四边形AHEF是矩形,
∴AF=HE=HB+BE=18,
∵∠ABC=∠AOE,,
∴.
在Rt△OAF中,.
∵OA2﹣OF2=AF2,
∴,
解得:OA=30,
∴车轮⊙O的直径是60cm.
