人教版数学8年级上册 12.2 三角形全等的判定 分层练习(含答案)
文档属性
| 名称 | 人教版数学8年级上册 12.2 三角形全等的判定 分层练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 190.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 15:30:11 | ||
图片预览



文档简介
三角形全等的判定——拓展课
班级: 组号: 姓名:
一、巩固训练
1.如图(2):AC∥EF,AC=EF,AE=BD.求证:△ABC≌△EDF。
2.如图,C为BE上一点,点A,D分别在BE两侧。AC=CD,AB=CE,BC=ED.AC与CD平行吗?请说明理由。
二、错题再现
1.如图:AB=DC,BE=CF,AF=DE。求证:△ABE≌△DCF。
2.已知:AD⊥BE,垂足C是BE的中点,AB=DE,则AB与DE有何位置关系?请说明理由。
三、能力提升
如图,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M。
(1)求证:AM=CM;
(2)当E、F两点移动到图所示的位置时,其他条件不变,上述结论能否成立?若成立,请给出证明;若不成立,请说明理由。
四、精练反馈
A组:
1.如图,AB=CD,CE=DF,AE=BF。求证:AE∥BF。
B组:
2.在四边形ABCD中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF。
(1)求证:DE=DF;
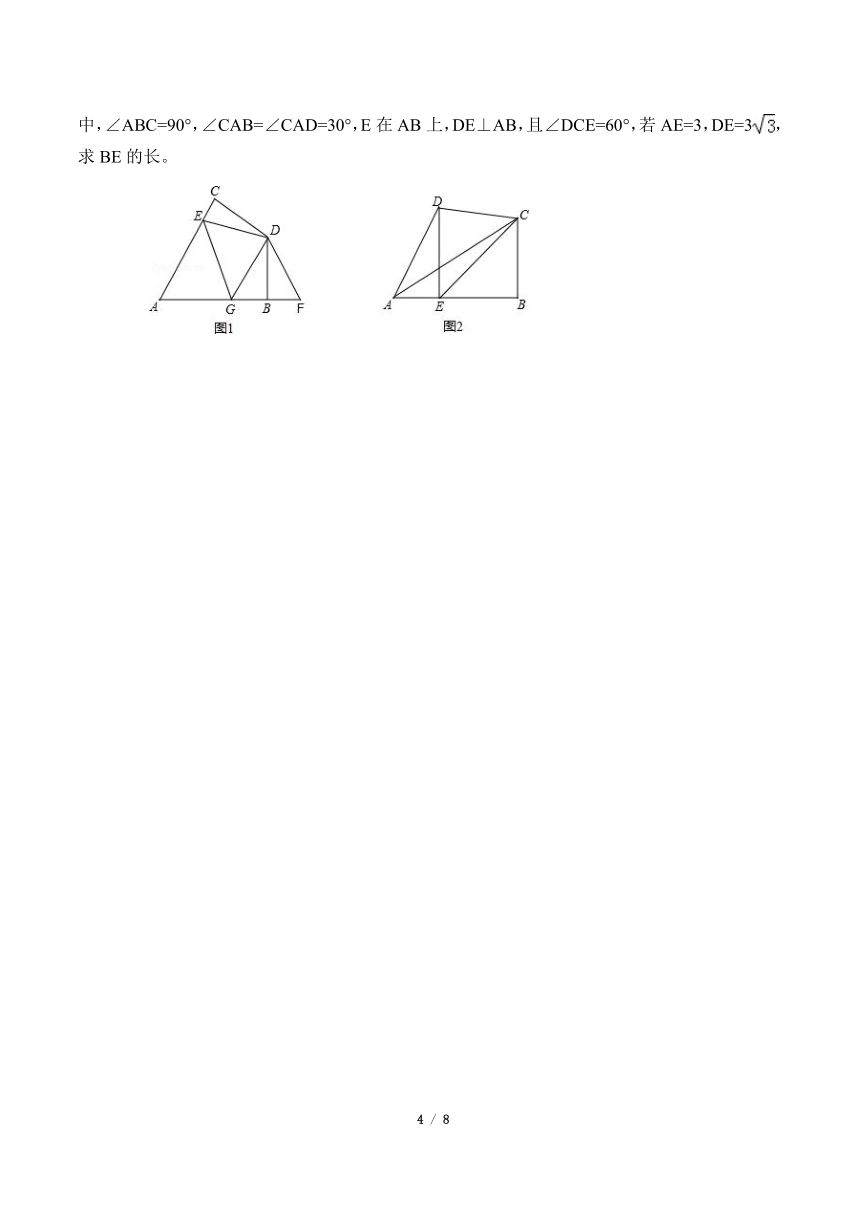
(2)在图1中,若G在AB上且∠EDG=60°,试猜想CE、EG、BG之间的数量关系并证明;
(3)若题中条件“∠CAB=60°且∠CDB=120°”改为∠CAB=α,∠CDB=180°-α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?(只写结果不要证明)
(4)运用(1)(2)(3)解答中所积累的经验和知识,完成下题:如图2,在四边形ABCD中,∠ABC=90°,∠CAB=∠CAD=30°,E在AB上,DE⊥AB,且∠DCE=60°,若AE=3,DE=3,求BE的长。
【答案】
巩固训练
1.证明:
∵AC∥EF
∴∠A=∠FED
在△ABC和△EDF中
∴△ABC≌△EDF(SAS)
2.答:AC∥CD
在△ABC和△DCE中
∴△ABC≌△DCE(SSS)
∵∠B=∠E
∴AC∥CD
错题再现
1.证明:在△ABE和△DCF中
∴△ABE≌△DCF(SSS)
2.答:AB∥DE
证明:∵AD⊥BE
∴∠ACB=∠DCE=90°
∵C是BE的中点
∴AC=CD
在△ACB和△ECD中
∴△ACB≌△ECD(SAS)
∴∠A=∠D
∴AB∥DE
能力提升
(1)证明:∵DE⊥AC BF⊥AC
∴∠AFB=∠BFM=∠DEC=∠DEM=90°
在Rt△BAF和Rt△CED中
∴Rt△BAF≌Rt△CED(HL)
∴BF=DF
在△BMF和△DME中
∴△BMF≌△DM(AAS)
∴MF=ME ∴MF+ AF= CE+ ME
∴AM=CM
(2)答:成立
∵AF=CE
∵DE⊥AC BF⊥AC
∴∠BFA =∠DEC =90°
在Rt△BAF和Rt△CED中
∴Rt△BAF≌Rt△CED(HL)
∴BF=DE
在△BFM和△DEM中
∴△BFM≌△DEM(AAS)
∴EM=NF
∴AM=CM
精练反馈
1.∵AB=CD ∴AB+BC=CD+BC ∴AC=BD
在△AEC和△BDF中
∴△AEC≌△BDF(SSS)
∴∠A=∠FBD
∴AE∥BF
2.(1)证明:连结∵
∴≌
∴
∴
在 和中,
∴≌。∴
(2)∵≌
∴。∴
∴
∴≌∴
(3)当时,
(4)过作,垂足为延长线上的点,∵
∴
∴∵
∴
∴由前面结论可得:
∴
7 / 8
班级: 组号: 姓名:
一、巩固训练
1.如图(2):AC∥EF,AC=EF,AE=BD.求证:△ABC≌△EDF。
2.如图,C为BE上一点,点A,D分别在BE两侧。AC=CD,AB=CE,BC=ED.AC与CD平行吗?请说明理由。
二、错题再现
1.如图:AB=DC,BE=CF,AF=DE。求证:△ABE≌△DCF。
2.已知:AD⊥BE,垂足C是BE的中点,AB=DE,则AB与DE有何位置关系?请说明理由。
三、能力提升
如图,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M。
(1)求证:AM=CM;
(2)当E、F两点移动到图所示的位置时,其他条件不变,上述结论能否成立?若成立,请给出证明;若不成立,请说明理由。
四、精练反馈
A组:
1.如图,AB=CD,CE=DF,AE=BF。求证:AE∥BF。
B组:
2.在四边形ABCD中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF。
(1)求证:DE=DF;
(2)在图1中,若G在AB上且∠EDG=60°,试猜想CE、EG、BG之间的数量关系并证明;
(3)若题中条件“∠CAB=60°且∠CDB=120°”改为∠CAB=α,∠CDB=180°-α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?(只写结果不要证明)
(4)运用(1)(2)(3)解答中所积累的经验和知识,完成下题:如图2,在四边形ABCD中,∠ABC=90°,∠CAB=∠CAD=30°,E在AB上,DE⊥AB,且∠DCE=60°,若AE=3,DE=3,求BE的长。
【答案】
巩固训练
1.证明:
∵AC∥EF
∴∠A=∠FED
在△ABC和△EDF中
∴△ABC≌△EDF(SAS)
2.答:AC∥CD
在△ABC和△DCE中
∴△ABC≌△DCE(SSS)
∵∠B=∠E
∴AC∥CD
错题再现
1.证明:在△ABE和△DCF中
∴△ABE≌△DCF(SSS)
2.答:AB∥DE
证明:∵AD⊥BE
∴∠ACB=∠DCE=90°
∵C是BE的中点
∴AC=CD
在△ACB和△ECD中
∴△ACB≌△ECD(SAS)
∴∠A=∠D
∴AB∥DE
能力提升
(1)证明:∵DE⊥AC BF⊥AC
∴∠AFB=∠BFM=∠DEC=∠DEM=90°
在Rt△BAF和Rt△CED中
∴Rt△BAF≌Rt△CED(HL)
∴BF=DF
在△BMF和△DME中
∴△BMF≌△DM(AAS)
∴MF=ME ∴MF+ AF= CE+ ME
∴AM=CM
(2)答:成立
∵AF=CE
∵DE⊥AC BF⊥AC
∴∠BFA =∠DEC =90°
在Rt△BAF和Rt△CED中
∴Rt△BAF≌Rt△CED(HL)
∴BF=DE
在△BFM和△DEM中
∴△BFM≌△DEM(AAS)
∴EM=NF
∴AM=CM
精练反馈
1.∵AB=CD ∴AB+BC=CD+BC ∴AC=BD
在△AEC和△BDF中
∴△AEC≌△BDF(SSS)
∴∠A=∠FBD
∴AE∥BF
2.(1)证明:连结∵
∴≌
∴
∴
在 和中,
∴≌。∴
(2)∵≌
∴。∴
∴
∴≌∴
(3)当时,
(4)过作,垂足为延长线上的点,∵
∴
∴∵
∴
∴由前面结论可得:
∴
7 / 8
