人教版数学8年级下册 17.1 勾股定理(2) 学案(含答案)
文档属性
| 名称 | 人教版数学8年级下册 17.1 勾股定理(2) 学案(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 151.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 00:00:00 | ||
图片预览


文档简介
勾股定理
班级:_____________姓名:__________________组号:_________
第二课时
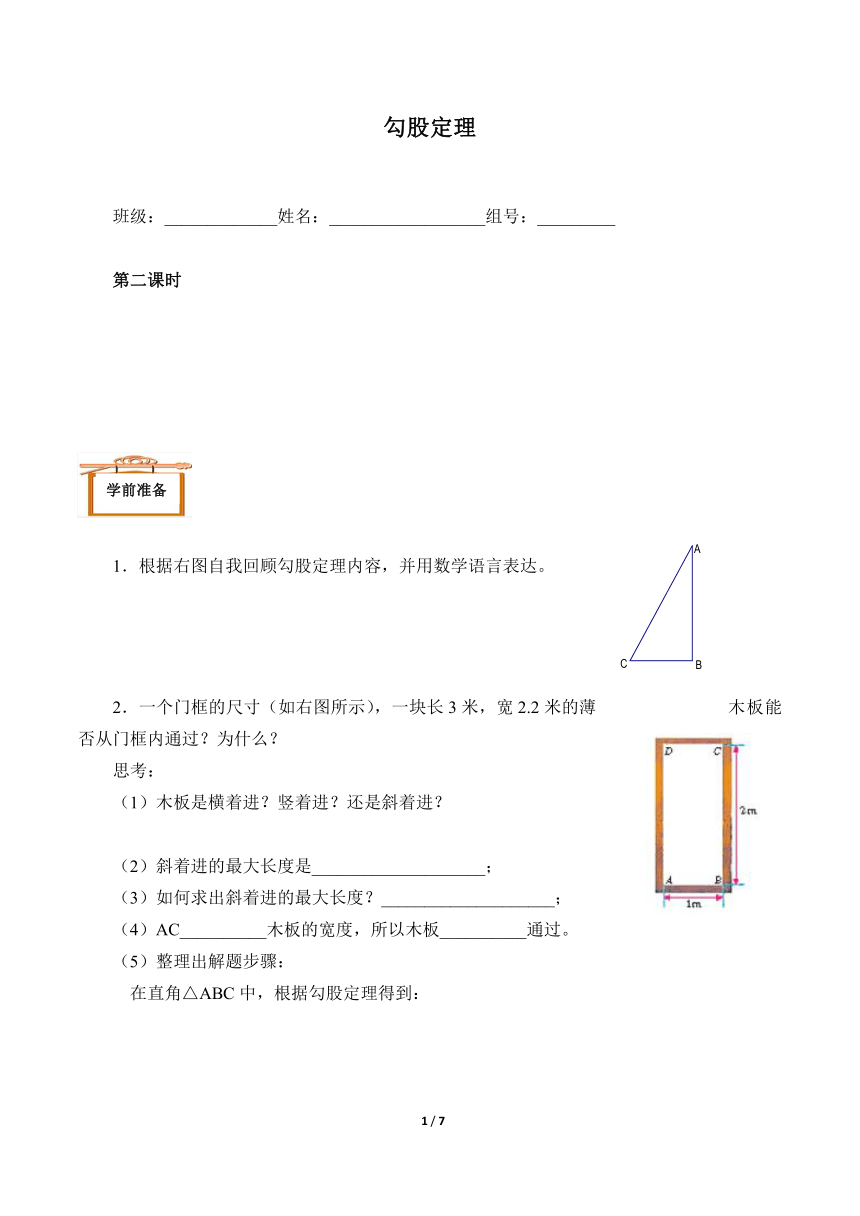
1.根据右图自我回顾勾股定理内容,并用数学语言表达。
2.一个门框的尺寸(如右图所示),一块长3米,宽2.2米的薄木板能否从门框内通过?为什么?
思考:
(1)木板是横着进?竖着进?还是斜着进?
(2)斜着进的最大长度是____________________;
(3)如何求出斜着进的最大长度?____________________;
(4)AC__________木板的宽度,所以木板__________通过。
(5)整理出解题步骤:
在直角△ABC中,根据勾股定理得到:
3.请在课本中分析例2的解题思路。
4.如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”。他们仅仅少走了__________米却踩伤了花草。
5.如图,去年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底部的距离比折断部分多1米,则这棵树折断之前的高度是多少米?(用方程解)
★通过预习你还有什么困惑?
一、课堂活动、记录
用勾股定理解决简单的实际问题时,是要把实际问题转化为在什么三角形中解决?
二、精练反馈
A组:
1.如图,将长为5米的梯子AC斜靠在墙上,BC长为3米,求梯子上端A到墙的底边的垂直距离AB=__________。
2.在Rt△ABC,∠C=90°,a、b为直角边,如果b=8,a:c=3:5,则c=__________。
B组:
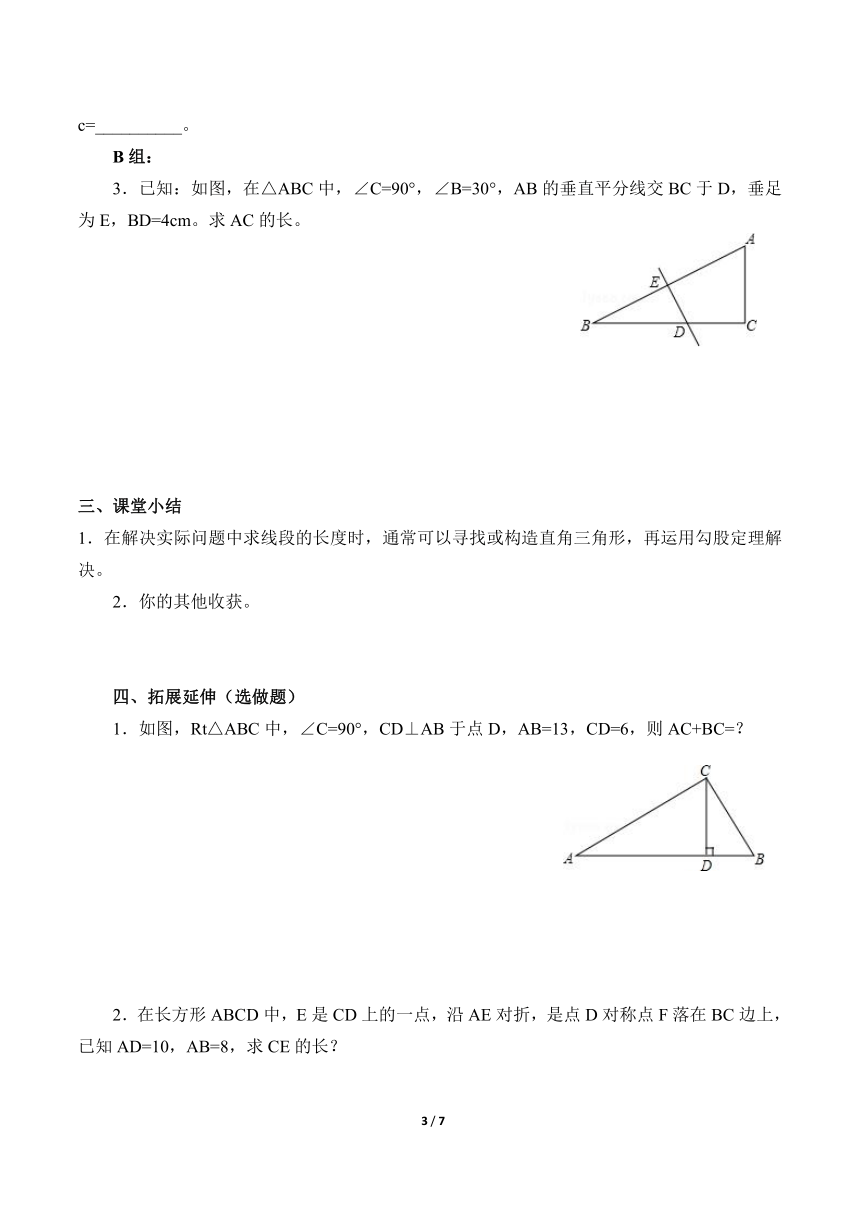
3.已知:如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,垂足为E,BD=4cm。求AC的长。
三、课堂小结
1.在解决实际问题中求线段的长度时,通常可以寻找或构造直角三角形,再运用勾股定理解决。
2.你的其他收获。
四、拓展延伸(选做题)
1.如图,Rt△ABC中,∠C=90°,CD⊥AB于点D,AB=13,CD=6,则AC+BC=?
2.在长方形ABCD中,E是CD上的一点,沿AE对折,是点D对称点F落在BC边上,已知AD=10,AB=8,求CE的长?
3.已知:如图,在△ABC中,AB=AC,D在CB的延长线上。
求证:(1)AD2-AB2=BD·CD;
(2)若D在CB上,结论如何,试证明你的结论。
【答案】
【学前准备】
1.
2.(1)斜着进
(2)
(3)
(4)>;可以
(5)
≈2.24米>2.2米。
所以木板能从门框内通过
3.略
4.2
5.∵AC=4米,BC=3米,∠ACB=90°,
∴折断的部分长为
∴折断前高度为5+3=8(米)
【课堂探究】
课堂活动、记录
略
精练反馈
1.4米
2.10
3.连接AD,
∵ED是AB的垂直平分线,
∴DB=DA=4cm,
∵∠B=30°,
∴∠ADC=2∠B=60°,
∴∠DAC=30°,
∴DC=2,
∵在△ABC中,∠C=90°
∴由勾股定理得:AC=
课堂小结
略
拓展延伸(选做题)
1.解:∵S△ABC=AB CD=AC BC,AB=13,CD=6,
∴AC BC=13×6=78,
∵△ABC为直角三角形,
∴根据勾股定理得:AB2=AC2+BC2=169,
∴(AC+BC)2=AC2+2AC BC+BC2=169+156=325,
则AC+BC=5。
2.解:∵四边形ABCD是矩形,
∴AD=BC=10cm,CD=AB=8cm,
根据题意得:Rt△ADE≌Rt△AFE,
∴∠AFE=90°,AF=10cm,EF=DE,
设CE=xcm,则DE=EF=CD-CE=8-x,
在Rt△ABF中由勾股定理得:AB2+BF2=AF2,
即82+BF2=102,
∴BF=6cm,
∴CF=BC-BF=10-6=4(cm),
在Rt△ECF中由勾股定理可得:EF2=CE2+CF2,
即(8-x)2=x2+42,
∴64-16x+x2=x2+16,
∴x=3(cm),
即CE=3cm。
3.(1)证明:如图,过点A作AE⊥BC于E,
∵AB=AC,
∴BE=CE,
在Rt△ADE中,AD2-AE2=DE2,
在Rt△ACE中,AC2-AE2=CE2,
两式相减得,AD2-AC2=DE2-CE2=(DE-CE)(DE+CE)=(DE-BE)CD=BD CD,即AD2-AB2=BD CD;
(2)结论为:AC2-AD2=BD CD.
证明如下:与(1)同理可得,AD2-AE2=DE2,AC2-AE2=CE2,
∵点D在CB上,
∴AB>AD,
∴AC2-AD2=CE2-DE2=(CE-DE)(CE+DE)=(BE-DE)(CE+DE)=BD CD,
即AC2-AD2=BD CD
学前准备
课堂探究
7 / 7
班级:_____________姓名:__________________组号:_________
第二课时
1.根据右图自我回顾勾股定理内容,并用数学语言表达。
2.一个门框的尺寸(如右图所示),一块长3米,宽2.2米的薄木板能否从门框内通过?为什么?
思考:
(1)木板是横着进?竖着进?还是斜着进?
(2)斜着进的最大长度是____________________;
(3)如何求出斜着进的最大长度?____________________;
(4)AC__________木板的宽度,所以木板__________通过。
(5)整理出解题步骤:
在直角△ABC中,根据勾股定理得到:
3.请在课本中分析例2的解题思路。
4.如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”。他们仅仅少走了__________米却踩伤了花草。
5.如图,去年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底部的距离比折断部分多1米,则这棵树折断之前的高度是多少米?(用方程解)
★通过预习你还有什么困惑?
一、课堂活动、记录
用勾股定理解决简单的实际问题时,是要把实际问题转化为在什么三角形中解决?
二、精练反馈
A组:
1.如图,将长为5米的梯子AC斜靠在墙上,BC长为3米,求梯子上端A到墙的底边的垂直距离AB=__________。
2.在Rt△ABC,∠C=90°,a、b为直角边,如果b=8,a:c=3:5,则c=__________。
B组:
3.已知:如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,垂足为E,BD=4cm。求AC的长。
三、课堂小结
1.在解决实际问题中求线段的长度时,通常可以寻找或构造直角三角形,再运用勾股定理解决。
2.你的其他收获。
四、拓展延伸(选做题)
1.如图,Rt△ABC中,∠C=90°,CD⊥AB于点D,AB=13,CD=6,则AC+BC=?
2.在长方形ABCD中,E是CD上的一点,沿AE对折,是点D对称点F落在BC边上,已知AD=10,AB=8,求CE的长?
3.已知:如图,在△ABC中,AB=AC,D在CB的延长线上。
求证:(1)AD2-AB2=BD·CD;
(2)若D在CB上,结论如何,试证明你的结论。
【答案】
【学前准备】
1.
2.(1)斜着进
(2)
(3)
(4)>;可以
(5)
≈2.24米>2.2米。
所以木板能从门框内通过
3.略
4.2
5.∵AC=4米,BC=3米,∠ACB=90°,
∴折断的部分长为
∴折断前高度为5+3=8(米)
【课堂探究】
课堂活动、记录
略
精练反馈
1.4米
2.10
3.连接AD,
∵ED是AB的垂直平分线,
∴DB=DA=4cm,
∵∠B=30°,
∴∠ADC=2∠B=60°,
∴∠DAC=30°,
∴DC=2,
∵在△ABC中,∠C=90°
∴由勾股定理得:AC=
课堂小结
略
拓展延伸(选做题)
1.解:∵S△ABC=AB CD=AC BC,AB=13,CD=6,
∴AC BC=13×6=78,
∵△ABC为直角三角形,
∴根据勾股定理得:AB2=AC2+BC2=169,
∴(AC+BC)2=AC2+2AC BC+BC2=169+156=325,
则AC+BC=5。
2.解:∵四边形ABCD是矩形,
∴AD=BC=10cm,CD=AB=8cm,
根据题意得:Rt△ADE≌Rt△AFE,
∴∠AFE=90°,AF=10cm,EF=DE,
设CE=xcm,则DE=EF=CD-CE=8-x,
在Rt△ABF中由勾股定理得:AB2+BF2=AF2,
即82+BF2=102,
∴BF=6cm,
∴CF=BC-BF=10-6=4(cm),
在Rt△ECF中由勾股定理可得:EF2=CE2+CF2,
即(8-x)2=x2+42,
∴64-16x+x2=x2+16,
∴x=3(cm),
即CE=3cm。
3.(1)证明:如图,过点A作AE⊥BC于E,
∵AB=AC,
∴BE=CE,
在Rt△ADE中,AD2-AE2=DE2,
在Rt△ACE中,AC2-AE2=CE2,
两式相减得,AD2-AC2=DE2-CE2=(DE-CE)(DE+CE)=(DE-BE)CD=BD CD,即AD2-AB2=BD CD;
(2)结论为:AC2-AD2=BD CD.
证明如下:与(1)同理可得,AD2-AE2=DE2,AC2-AE2=CE2,
∵点D在CB上,
∴AB>AD,
∴AC2-AD2=CE2-DE2=(CE-DE)(CE+DE)=(BE-DE)(CE+DE)=BD CD,
即AC2-AD2=BD CD
学前准备
课堂探究
7 / 7
