第五章 圆培优专题 圆与锐角三角函数(含答案)
文档属性
| 名称 | 第五章 圆培优专题 圆与锐角三角函数(含答案) | 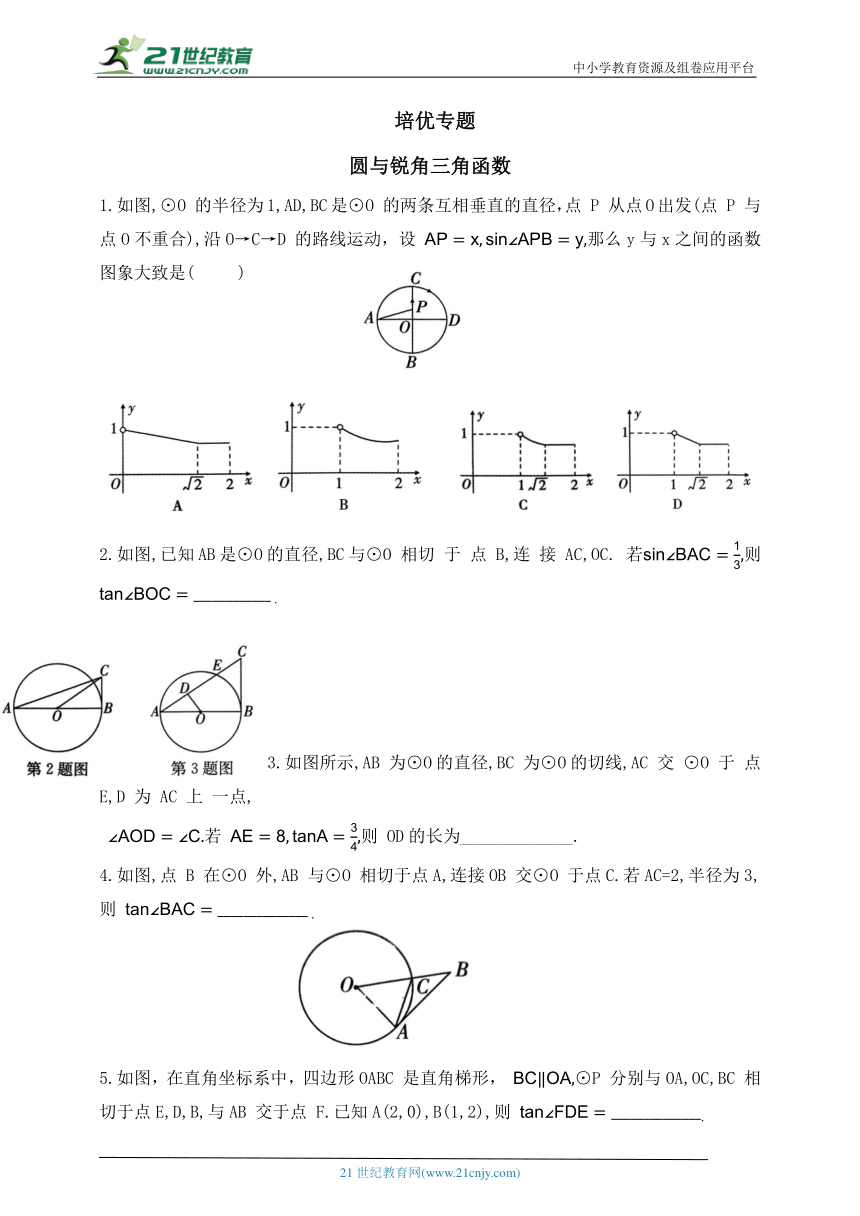 | |
| 格式 | docx | ||
| 文件大小 | 22.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 21:18:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
培优专题
圆与锐角三角函数
1.如图,⊙O 的半径为1,AD,BC是⊙O 的两条互相垂直的直径,点 P 从点O出发(点 P 与点O不重合),沿O→C→D 的路线运动,设 那么y与x之间的函数图象大致是( )
2.如图,已知AB是⊙O的直径,BC与⊙O 相切 于 点 B,连 接 AC,OC. 若则
3.如图所示,AB 为⊙O的直径,BC 为⊙O的切线,AC 交 ⊙O 于 点 E,D 为 AC 上 一点,
若 则 OD的长为_____________.
4.如图,点 B 在⊙O 外,AB 与⊙O 相切于点A,连接OB 交⊙O 于点C.若AC=2,半径为3,则
5.如图,在直角坐标系中,四边形OABC 是直角梯形, ⊙P 分别与OA,OC,BC 相切于点E,D,B,与AB 交于点 F.已知A(2,0),B(1,2),则
6.[几何直观]如图,矩形 ABCD 中, 以AB为直径在矩形内作半圆,DE切⊙O 于点E,则
7.[推理能力]如图,C,D 为⊙O 上两点,且在直径AB 两侧,连接CD 交AB 于点E,G 是 上一点,
(1)求证:
(2)点C 关于DG 的对称点为 F,连接CF.当点 F 落在直径AB 上时, 求⊙O 的半径.
参考答案
1. C
[解析]∵AB 是⊙O 的直径,BC 与⊙O 相切于点 B,∴设
3.3
[解析]如图,作直径AD,连接CD.∵AB 与⊙O 相切于点A,∴OA⊥AB,∴∠DAB=90°,即. =90°.∵AD为直径, 即 90°, ∴ ∠D = ∠BAC. 在 Rt △ADC 中,
[解析]如图,连接 PB,PE.∵⊙P 分别与OA,BC相切于点E,B,. ∴点 B,P,E 在一条直线上.∵A(2,0),B(1,2),∴AE=1,BE=
[解析]如图,连接DO,OE,设 FC=x.∵AD,DE 都是⊙O的切线,∴DA=DE=3.又∵EF,FB 都是⊙O的切线,∴EF=FB=3-x,∴在 Rt△DCF 中,由勾股定理得
7.(1)证明: AB 为⊙O的直径,
(2)解:如图,连接 DF.
AB 是⊙O 的直径,∴AB⊥CD,CE=DE,∴FD=FC=10.∵点C,F 关于DG 对称,∴DC=DF=10
∴⊙O的半径为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
培优专题
圆与锐角三角函数
1.如图,⊙O 的半径为1,AD,BC是⊙O 的两条互相垂直的直径,点 P 从点O出发(点 P 与点O不重合),沿O→C→D 的路线运动,设 那么y与x之间的函数图象大致是( )
2.如图,已知AB是⊙O的直径,BC与⊙O 相切 于 点 B,连 接 AC,OC. 若则
3.如图所示,AB 为⊙O的直径,BC 为⊙O的切线,AC 交 ⊙O 于 点 E,D 为 AC 上 一点,
若 则 OD的长为_____________.
4.如图,点 B 在⊙O 外,AB 与⊙O 相切于点A,连接OB 交⊙O 于点C.若AC=2,半径为3,则
5.如图,在直角坐标系中,四边形OABC 是直角梯形, ⊙P 分别与OA,OC,BC 相切于点E,D,B,与AB 交于点 F.已知A(2,0),B(1,2),则
6.[几何直观]如图,矩形 ABCD 中, 以AB为直径在矩形内作半圆,DE切⊙O 于点E,则
7.[推理能力]如图,C,D 为⊙O 上两点,且在直径AB 两侧,连接CD 交AB 于点E,G 是 上一点,
(1)求证:
(2)点C 关于DG 的对称点为 F,连接CF.当点 F 落在直径AB 上时, 求⊙O 的半径.
参考答案
1. C
[解析]∵AB 是⊙O 的直径,BC 与⊙O 相切于点 B,∴设
3.3
[解析]如图,作直径AD,连接CD.∵AB 与⊙O 相切于点A,∴OA⊥AB,∴∠DAB=90°,即. =90°.∵AD为直径, 即 90°, ∴ ∠D = ∠BAC. 在 Rt △ADC 中,
[解析]如图,连接 PB,PE.∵⊙P 分别与OA,BC相切于点E,B,. ∴点 B,P,E 在一条直线上.∵A(2,0),B(1,2),∴AE=1,BE=
[解析]如图,连接DO,OE,设 FC=x.∵AD,DE 都是⊙O的切线,∴DA=DE=3.又∵EF,FB 都是⊙O的切线,∴EF=FB=3-x,∴在 Rt△DCF 中,由勾股定理得
7.(1)证明: AB 为⊙O的直径,
(2)解:如图,连接 DF.
AB 是⊙O 的直径,∴AB⊥CD,CE=DE,∴FD=FC=10.∵点C,F 关于DG 对称,∴DC=DF=10
∴⊙O的半径为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
