12.3角的平分线的性质的综合运用 教学设计(表格式)
文档属性
| 名称 | 12.3角的平分线的性质的综合运用 教学设计(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 119.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 00:00:00 | ||
图片预览


文档简介
课题 角的平分线的性质的综合运用
教学目标
教学目标:综合运用角的平分线的性质的两个定理解决问题,并学习结合之前的知识(如全 等三角形等)解决更为综合的问题. 教学重点:识别基本图,分析推理,整合思路,规范书写,反思优化. 教学难点:通过分析进行合理的推理和优化.
教学过程
时 间 教学 环节 主要师生活动
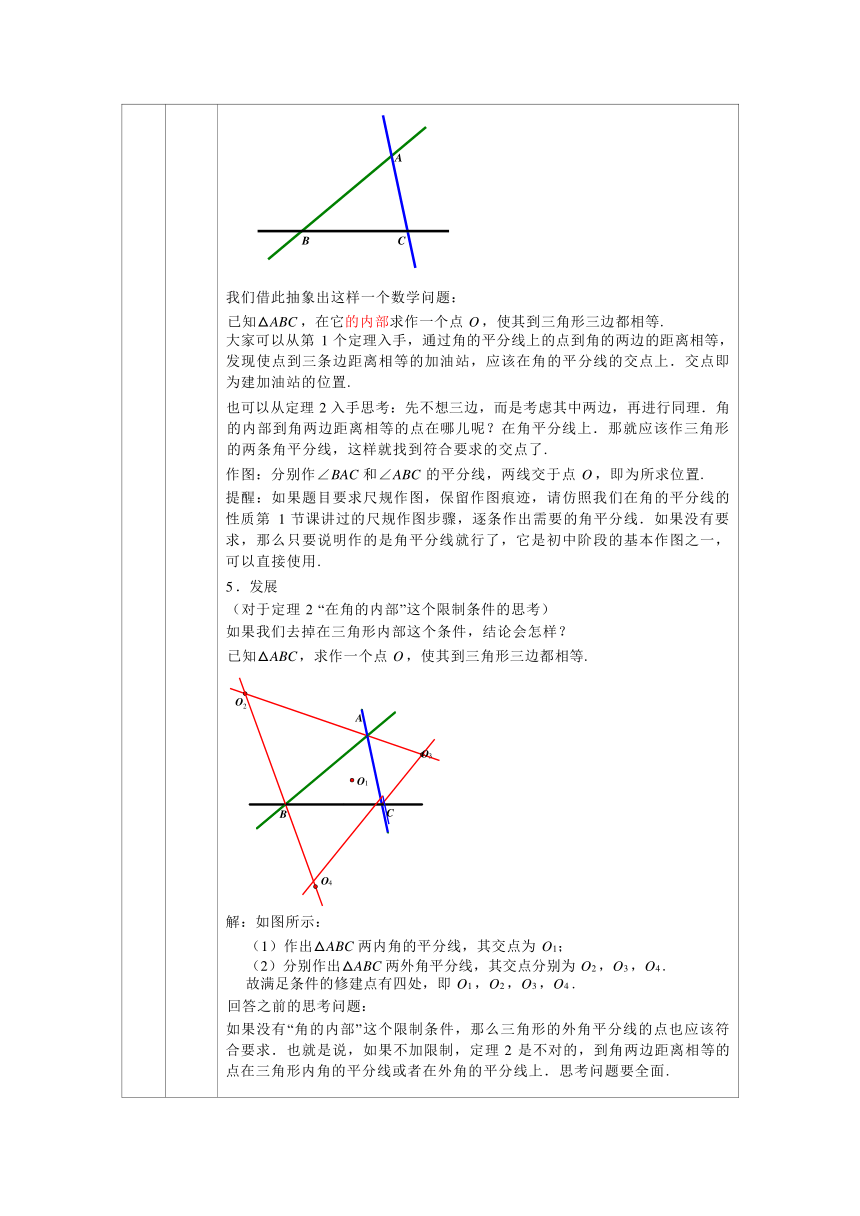
2 分 钟 8- 10 分 钟 复 习 定理 回 顾 整合 复习定理 1 .角平分线的性质:角平分线上的点到角的两边的距离相等. 符号表示: ∵OP 平分∠AOB, PD⊥OA ,PE⊥OB, ∴PD=PE . 2 .交换题设结论(注意附加条件):角的内部到角的两边的距离相等的点在 角的平分线上. 符号表示: ∵ PD⊥OA ,PE⊥OB ,PD=PE, ∴点 P 在∠AOB 的平分线上. 我们上节课还留下了一个思考问题:为什么定理 2 会附加角的内部这个条件? 我们先通过研究相关的一系列问题,来回答并帮助大家进行近期学习内容的 复习.
【问题】 1 .回顾 A N (
M
)P B C
之前的课上我们研究过这样一个书上的问题: (教材 50 页 例题)如图,△ABC 的角平分线 BM,CN 相交于 P . 求证:点 P 到三边 AB ,BC,CA 的距离相等. 解题思路:过点 P 分别向三角形各边作垂直,标垂足. 由角的平分线的性质得 PD= PE 及 PE= PF. 进而 PD= PE = PF.于是问题得证. 2 .追问 点 P 在∠BAC 的平分线上吗?这说明三角形的三条角平分线有什么关系? ∵PD =PE =PF(已证), 又 PD⊥AB ,PF⊥AC, ∴点 P 在∠BAC 的平分线上(角的内部到角的两边的距离相等的点在角的 平分线上). 由此可知:三角形的三条角平分线交于一点. 我们之前用角的平分线的性质来验证三角形两条角的平分线的交点到三 边距离相等,现在再通过定理 2 来判断这个交点也在第三条角平分线上.
(
D
) (
P
) (
E
) (
C
●
)3 .类比 A B
(教材 50 页 练习 第 2 题)如图,△ABC 的∠ABC 外角的平分线 BD 与∠ACB 的外角的平分线 CE 相交于点 P .(1)求证:点 P 到三边 AB ,BC ,CA 所在 的直线的距离相等. 思路:过点 P 分别向三角形各边作垂直,标垂足.由角的平分线的性质得 PF =PG 及 PG =PH.进而 PF=PG =PH.于是问题得证. 过点 P 作 PF,PG ,PH 分别垂直于 AB ,BC ,CA ,垂足分别为 F, G ,H. ∵BD 为∠ABC 外角的平分线,点 P 在 BD 上, ∴PF=PG .(角的平分线上的点到这个角两边的距离相等) 同理 PG =PH. ∴PF=PG =PH. 即点 P 到三边 AB ,BC,CA 所在的直线的距离相等. (2)点 P 在∠BAC 的平分线上吗?这说明三角形的相邻两个外角的平分线与 第三个内角角平分线有什么关系? ∵PM⊥AF,PN⊥BC, ∴点 P 在∠BAC 的平分线上(角的内部到角的两边的距离相等的点在角的 平分线上). 由此可知:三角形的相邻两个外角的平分线与第三个角的角平分线交于一点. 4 .应用 (教材 P55 复习题 12 第 6 题)如图,为了促进当地旅游发展,某地要在三 条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的 距离相等,应在何处修建?
(
B
C
) (
O
2
) (
B
) (
C
) (
A
) 我们借此抽象出这样一个数学问题: 已知△ABC ,在它的内部求作一个点 O ,使其到三角形三边都相等. 大家可以从第 1 个定理入手,通过角的平分线上的点到角的两边的距离相等, 发现使点到三条边距离相等的加油站,应该在角的平分线的交点上.交点即 为建加油站的位置. 也可以从定理 2 入手思考:先不想三边,而是考虑其中两边,再进行同理.角 的内部到角两边距离相等的点在哪儿呢?在角平分线上.那就应该作三角形 的两条角平分线,这样就找到符合要求的交点了. 作图:分别作∠BAC 和∠ABC 的平分线,两线交于点 O ,即为所求位置. 提醒:如果题目要求尺规作图,保留作图痕迹,请仿照我们在角的平分线的 性质第 1 节课讲过的尺规作图步骤,逐条作出需要的角平分线.如果没有要 求,那么只要说明作的是角平分线就行了,它是初中阶段的基本作图之一, 可以直接使用. 5 .发展 (对于定理 2 “在角的内部”这个限制条件的思考) 如果我们去掉在三角形内部这个条件,结论会怎样? 已知△ABC ,求作一个点 O ,使其到三角形三边都相等. (
A
O
3
O
1
) (
O
4
) 解:如图所示: (1)作出△ABC 两内角的平分线,其交点为 O1; (2)分别作出△ABC 两外角平分线,其交点分别为 O2 ,O3 ,O4 . 故满足条件的修建点有四处,即 O1 ,O2 ,O3 ,O4 . 回答之前的思考问题: 如果没有“角的内部”这个限制条件,那么三角形的外角平分线的点也应该符 合要求.也就是说,如果不加限制,定理 2 是不对的,到角两边距离相等的 点在三角形内角的平分线或者在外角的平分线上.思考问题要全面.
4-5 分 钟 6-8 分 钟 例 题 讲解 例 1 .(改编教材 51 页 习题 12 .3 第 4 题)如图,在△ABC 中,点 D ,E,F 在边 BC 上,点 P 在线段 AD 上,若 PE∥AB,PF∥AC,点 D 到 PE 和 PF 的距离相等.求证:点 D 到 AB 和 AC 的距离相等.
(
A
.
P
)
B E D F C
分析:标图 题目出现了两次“点到角两边的距离相等 ”, 1 .“点到角两边的距离相等” 当已知,想定理 2;当求证,想定理 1 2 .平行线用以转换角的位置 整理思路: 处理这个问题分 3 步走: 先用定理 2 证等角;再用平行关系换角的位置;最后用定理 1 再证距离相等. 证明: ∵点 D 到 PE 和 PF 的距离相等, ∴PD 是∠EPF 的平分线(定理 2). ∴∠1 = ∠2 . ∵PE∥AB , ∴∠1 = ∠3 . 同理, ∠2 = ∠4 . ∴∠3 = ∠4 . ∴△ABC 中,AD 平分∠BAC . ∴点 D 到 AB 和 AC 的距离相等. 点评:本题综合性较强,大家可以先通过分析结论,找到证明中使用到的的 板块,再展开书写.我们会发现这个题使用了这部分内容学到的两个定理, 解题的关键就是熟记和鉴别这两个定理.为了避免叙述角时发生混乱,可以 引入序号编角,叙述距离时如果不是必须,可以省略作出垂直的图形? 例 2 .(教材 51 页 习题 12 .3 第 5 题)如图,OC 是∠AOB 的平分线,P 是 OC 上一点,PD⊥OA ,PE⊥OB ,垂足分别为 D ,E .F 是 OC 上另一点, 连接 DF,EF.求证:DF=EF.
(
●
) (
●
) (
A
) (
P
) (
.
F
) (
D
) (
●
)C O E B
分析: 已知可推? “角分双垂推相等 ” 根据角平分线的性质可得 PD =PE, 进而可能推出△ODP≌△OEP 或△PDF≌△PEF.
(
l
OP
=
OP
,
)求证何来?可能来自全等. △ODF≌△OEF 或△PDF≌△PEF. 证明: 法 1 分三步,先由角的平分线的性质由 PD =PE; 再结合 OP =OP 证出 Rt△ODP≌Rt△OEP(HL),根据全等三角形的性质可得出 OD =OE;最后结 合∠DOF = ∠EOF,OF=OF 可证出△ODF≌△OEF(SAS),再利用全等三 角形的性质即可证出 DF=EF. ∵点 P 在∠AOB 的平分线上, ∴∠DOP = ∠EOP . 又 PD⊥OA ,PE⊥OB, ∴PD =PE . 在 Rt△ODP≌Rt△OEP 中 (
〈
)(PD = PE, ∴Rt△ODP≌Rt△OEP(HL). ∴OD =OE . 在△ODF 和△OEF 中, 〈EOF, ∴△ODF≌△OEF(SAS). ∴DF=EF. 法 2 调整一下,既然由 PD =PE ,可能推出△PDF≌△PEF,求证 DF =EF 也可能来自△PDF≌△PEF,有没有可能只证明这一次全等呢?这就需要中间 证明∠DPF= ∠EPF 了,可以看到它们作为 Rt△POD 与 Rt△POE 的外角是可 以推证相等的. 也分三步,还是先由角的平分线的性质由 PD =PE;再推出作为 Rt△POD 和 Rt△POE 的外角, ∠OPD = ∠OPE;最后证出△PDF≌△PEF(SAS),再利 用全等三角形的性质即可证出 DF=EF. ∵PD⊥OA ,PE⊥OB, ∴∠ODP = ∠OEP =90 ° . 又点 P 在∠AOB 的平分线上, ∴∠DOP = ∠EOP ,PD =PE . ∵∠DPF=∠ODP+∠DOP, ∠EPF=∠OEP+∠EOP, ∴∠DPF=∠EPF. 在△PDF≌△PEF 中 (
〈
|
经
DPF
= 经
EPF
,
|l
PF
=
PF
,
∴
△
PDF
≌△
PEF
(
SAS
).
)( PD = PE,
2-3 分 钟 小 结 与 作 业 ∴DF=EF. 点评:决定题目的复杂性的,不仅仅是使用定理的多少,还有就是采用不同 的定理可能会产生不同的证明步骤,有时候这种步骤的差别是很大的,会体 现在书写耗时,便捷程度等各个方面.大家在处理问题的时候,最好能够在 会做的基础上要求自己做对,在做对的基础上,还可以要求更高,要做得好. 小结 1 .我们在这阶段学习了两个定理,需注意区分它们的条件和结论,以免发生 混淆. 2 .有些几何问题的解决需要添加辅助线,目前常见的辅助线以补全基本图为 主. 3 .一般的分析方法:已知可推什么?求证从哪里来?找常见基本图与基本说 法等.可以先思考核心步骤再展开写以免干扰思路. 4 .有时候解决问题的方法不止一种,步骤难度可能差不多也可能有优劣. 希望大家多尝试,多比较,多思考,多积累,逐步做到会-对-好. 课后作业 1 .如图, △ABC 的角平分线 AP 和外角平分线 BP 相交于点 P ,求证: 点 P 也在∠BCD 的平分线上. 分析:作 PF⊥AB 于 F,PG⊥BC 于 G,PH⊥AC 于 H,根据角平分线的性 质定理和判定定理证明即可. 证明:作 PF⊥AB 于 F,PG⊥BC 于 G ,PH⊥AC 于 H, ∵BP 是∠EBC 的平分线,PF⊥AB ,PG⊥BC, ∴PF=PG, ∵AP 是∠BAC 的平分线,PH⊥AC,PF⊥AB, ∴PH=PF, ∴PG =PH,PG⊥BC,PH⊥AC, ∴点 P 在∠BCD 的平分线上.
(
P
) (
C
●
)D A B E
2 .如图,AD 是△ABC 的角平分线,DE⊥AB ,DF⊥AC,垂足分别为 E ,F, 连接 EF,EF 交 AD 于点 G ,AD 与 EF 垂直吗?证明你的结论. 分析: 已知可推? 除得到等角和直角外,还由角的平分线的性质得到 DE =
DF.求证何来?可证 AD 与 EF 相交所成的四个角中,任意一个为直角.两 者如何联系?可证△DEG≌△DFG(SAS).
解:AD 垂直 EF.理由如下: ∵AD 为△ABC 的角平分线,① ∴∠1 = ∠2 . ∵DE⊥AB 于 E ,DF⊥AC 于 F,② ∴∠AED = ∠AFD =90 ° . ∴Rt△AED 与 Rt△AFD 中, ∠3 = ∠4 . 由①② , 得 DE =DF. 在△DEG 与△DFG 中, (|DE = DF, 〈|l , ∴△DEG≌△DFG(SAS). ∴∠DGE = ∠DGF=90 ° . ∴AD 垂直 EF.
教学目标
教学目标:综合运用角的平分线的性质的两个定理解决问题,并学习结合之前的知识(如全 等三角形等)解决更为综合的问题. 教学重点:识别基本图,分析推理,整合思路,规范书写,反思优化. 教学难点:通过分析进行合理的推理和优化.
教学过程
时 间 教学 环节 主要师生活动
2 分 钟 8- 10 分 钟 复 习 定理 回 顾 整合 复习定理 1 .角平分线的性质:角平分线上的点到角的两边的距离相等. 符号表示: ∵OP 平分∠AOB, PD⊥OA ,PE⊥OB, ∴PD=PE . 2 .交换题设结论(注意附加条件):角的内部到角的两边的距离相等的点在 角的平分线上. 符号表示: ∵ PD⊥OA ,PE⊥OB ,PD=PE, ∴点 P 在∠AOB 的平分线上. 我们上节课还留下了一个思考问题:为什么定理 2 会附加角的内部这个条件? 我们先通过研究相关的一系列问题,来回答并帮助大家进行近期学习内容的 复习.
【问题】 1 .回顾 A N (
M
)P B C
之前的课上我们研究过这样一个书上的问题: (教材 50 页 例题)如图,△ABC 的角平分线 BM,CN 相交于 P . 求证:点 P 到三边 AB ,BC,CA 的距离相等. 解题思路:过点 P 分别向三角形各边作垂直,标垂足. 由角的平分线的性质得 PD= PE 及 PE= PF. 进而 PD= PE = PF.于是问题得证. 2 .追问 点 P 在∠BAC 的平分线上吗?这说明三角形的三条角平分线有什么关系? ∵PD =PE =PF(已证), 又 PD⊥AB ,PF⊥AC, ∴点 P 在∠BAC 的平分线上(角的内部到角的两边的距离相等的点在角的 平分线上). 由此可知:三角形的三条角平分线交于一点. 我们之前用角的平分线的性质来验证三角形两条角的平分线的交点到三 边距离相等,现在再通过定理 2 来判断这个交点也在第三条角平分线上.
(
D
) (
P
) (
E
) (
C
●
)3 .类比 A B
(教材 50 页 练习 第 2 题)如图,△ABC 的∠ABC 外角的平分线 BD 与∠ACB 的外角的平分线 CE 相交于点 P .(1)求证:点 P 到三边 AB ,BC ,CA 所在 的直线的距离相等. 思路:过点 P 分别向三角形各边作垂直,标垂足.由角的平分线的性质得 PF =PG 及 PG =PH.进而 PF=PG =PH.于是问题得证. 过点 P 作 PF,PG ,PH 分别垂直于 AB ,BC ,CA ,垂足分别为 F, G ,H. ∵BD 为∠ABC 外角的平分线,点 P 在 BD 上, ∴PF=PG .(角的平分线上的点到这个角两边的距离相等) 同理 PG =PH. ∴PF=PG =PH. 即点 P 到三边 AB ,BC,CA 所在的直线的距离相等. (2)点 P 在∠BAC 的平分线上吗?这说明三角形的相邻两个外角的平分线与 第三个内角角平分线有什么关系? ∵PM⊥AF,PN⊥BC, ∴点 P 在∠BAC 的平分线上(角的内部到角的两边的距离相等的点在角的 平分线上). 由此可知:三角形的相邻两个外角的平分线与第三个角的角平分线交于一点. 4 .应用 (教材 P55 复习题 12 第 6 题)如图,为了促进当地旅游发展,某地要在三 条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的 距离相等,应在何处修建?
(
B
C
) (
O
2
) (
B
) (
C
) (
A
) 我们借此抽象出这样一个数学问题: 已知△ABC ,在它的内部求作一个点 O ,使其到三角形三边都相等. 大家可以从第 1 个定理入手,通过角的平分线上的点到角的两边的距离相等, 发现使点到三条边距离相等的加油站,应该在角的平分线的交点上.交点即 为建加油站的位置. 也可以从定理 2 入手思考:先不想三边,而是考虑其中两边,再进行同理.角 的内部到角两边距离相等的点在哪儿呢?在角平分线上.那就应该作三角形 的两条角平分线,这样就找到符合要求的交点了. 作图:分别作∠BAC 和∠ABC 的平分线,两线交于点 O ,即为所求位置. 提醒:如果题目要求尺规作图,保留作图痕迹,请仿照我们在角的平分线的 性质第 1 节课讲过的尺规作图步骤,逐条作出需要的角平分线.如果没有要 求,那么只要说明作的是角平分线就行了,它是初中阶段的基本作图之一, 可以直接使用. 5 .发展 (对于定理 2 “在角的内部”这个限制条件的思考) 如果我们去掉在三角形内部这个条件,结论会怎样? 已知△ABC ,求作一个点 O ,使其到三角形三边都相等. (
A
O
3
O
1
) (
O
4
) 解:如图所示: (1)作出△ABC 两内角的平分线,其交点为 O1; (2)分别作出△ABC 两外角平分线,其交点分别为 O2 ,O3 ,O4 . 故满足条件的修建点有四处,即 O1 ,O2 ,O3 ,O4 . 回答之前的思考问题: 如果没有“角的内部”这个限制条件,那么三角形的外角平分线的点也应该符 合要求.也就是说,如果不加限制,定理 2 是不对的,到角两边距离相等的 点在三角形内角的平分线或者在外角的平分线上.思考问题要全面.
4-5 分 钟 6-8 分 钟 例 题 讲解 例 1 .(改编教材 51 页 习题 12 .3 第 4 题)如图,在△ABC 中,点 D ,E,F 在边 BC 上,点 P 在线段 AD 上,若 PE∥AB,PF∥AC,点 D 到 PE 和 PF 的距离相等.求证:点 D 到 AB 和 AC 的距离相等.
(
A
.
P
)
B E D F C
分析:标图 题目出现了两次“点到角两边的距离相等 ”, 1 .“点到角两边的距离相等” 当已知,想定理 2;当求证,想定理 1 2 .平行线用以转换角的位置 整理思路: 处理这个问题分 3 步走: 先用定理 2 证等角;再用平行关系换角的位置;最后用定理 1 再证距离相等. 证明: ∵点 D 到 PE 和 PF 的距离相等, ∴PD 是∠EPF 的平分线(定理 2). ∴∠1 = ∠2 . ∵PE∥AB , ∴∠1 = ∠3 . 同理, ∠2 = ∠4 . ∴∠3 = ∠4 . ∴△ABC 中,AD 平分∠BAC . ∴点 D 到 AB 和 AC 的距离相等. 点评:本题综合性较强,大家可以先通过分析结论,找到证明中使用到的的 板块,再展开书写.我们会发现这个题使用了这部分内容学到的两个定理, 解题的关键就是熟记和鉴别这两个定理.为了避免叙述角时发生混乱,可以 引入序号编角,叙述距离时如果不是必须,可以省略作出垂直的图形? 例 2 .(教材 51 页 习题 12 .3 第 5 题)如图,OC 是∠AOB 的平分线,P 是 OC 上一点,PD⊥OA ,PE⊥OB ,垂足分别为 D ,E .F 是 OC 上另一点, 连接 DF,EF.求证:DF=EF.
(
●
) (
●
) (
A
) (
P
) (
.
F
) (
D
) (
●
)C O E B
分析: 已知可推? “角分双垂推相等 ” 根据角平分线的性质可得 PD =PE, 进而可能推出△ODP≌△OEP 或△PDF≌△PEF.
(
l
OP
=
OP
,
)求证何来?可能来自全等. △ODF≌△OEF 或△PDF≌△PEF. 证明: 法 1 分三步,先由角的平分线的性质由 PD =PE; 再结合 OP =OP 证出 Rt△ODP≌Rt△OEP(HL),根据全等三角形的性质可得出 OD =OE;最后结 合∠DOF = ∠EOF,OF=OF 可证出△ODF≌△OEF(SAS),再利用全等三 角形的性质即可证出 DF=EF. ∵点 P 在∠AOB 的平分线上, ∴∠DOP = ∠EOP . 又 PD⊥OA ,PE⊥OB, ∴PD =PE . 在 Rt△ODP≌Rt△OEP 中 (
〈
)(PD = PE, ∴Rt△ODP≌Rt△OEP(HL). ∴OD =OE . 在△ODF 和△OEF 中, 〈EOF, ∴△ODF≌△OEF(SAS). ∴DF=EF. 法 2 调整一下,既然由 PD =PE ,可能推出△PDF≌△PEF,求证 DF =EF 也可能来自△PDF≌△PEF,有没有可能只证明这一次全等呢?这就需要中间 证明∠DPF= ∠EPF 了,可以看到它们作为 Rt△POD 与 Rt△POE 的外角是可 以推证相等的. 也分三步,还是先由角的平分线的性质由 PD =PE;再推出作为 Rt△POD 和 Rt△POE 的外角, ∠OPD = ∠OPE;最后证出△PDF≌△PEF(SAS),再利 用全等三角形的性质即可证出 DF=EF. ∵PD⊥OA ,PE⊥OB, ∴∠ODP = ∠OEP =90 ° . 又点 P 在∠AOB 的平分线上, ∴∠DOP = ∠EOP ,PD =PE . ∵∠DPF=∠ODP+∠DOP, ∠EPF=∠OEP+∠EOP, ∴∠DPF=∠EPF. 在△PDF≌△PEF 中 (
〈
|
经
DPF
= 经
EPF
,
|l
PF
=
PF
,
∴
△
≌△
PEF
(
SAS
).
)( PD = PE,
2-3 分 钟 小 结 与 作 业 ∴DF=EF. 点评:决定题目的复杂性的,不仅仅是使用定理的多少,还有就是采用不同 的定理可能会产生不同的证明步骤,有时候这种步骤的差别是很大的,会体 现在书写耗时,便捷程度等各个方面.大家在处理问题的时候,最好能够在 会做的基础上要求自己做对,在做对的基础上,还可以要求更高,要做得好. 小结 1 .我们在这阶段学习了两个定理,需注意区分它们的条件和结论,以免发生 混淆. 2 .有些几何问题的解决需要添加辅助线,目前常见的辅助线以补全基本图为 主. 3 .一般的分析方法:已知可推什么?求证从哪里来?找常见基本图与基本说 法等.可以先思考核心步骤再展开写以免干扰思路. 4 .有时候解决问题的方法不止一种,步骤难度可能差不多也可能有优劣. 希望大家多尝试,多比较,多思考,多积累,逐步做到会-对-好. 课后作业 1 .如图, △ABC 的角平分线 AP 和外角平分线 BP 相交于点 P ,求证: 点 P 也在∠BCD 的平分线上. 分析:作 PF⊥AB 于 F,PG⊥BC 于 G,PH⊥AC 于 H,根据角平分线的性 质定理和判定定理证明即可. 证明:作 PF⊥AB 于 F,PG⊥BC 于 G ,PH⊥AC 于 H, ∵BP 是∠EBC 的平分线,PF⊥AB ,PG⊥BC, ∴PF=PG, ∵AP 是∠BAC 的平分线,PH⊥AC,PF⊥AB, ∴PH=PF, ∴PG =PH,PG⊥BC,PH⊥AC, ∴点 P 在∠BCD 的平分线上.
(
P
) (
C
●
)D A B E
2 .如图,AD 是△ABC 的角平分线,DE⊥AB ,DF⊥AC,垂足分别为 E ,F, 连接 EF,EF 交 AD 于点 G ,AD 与 EF 垂直吗?证明你的结论. 分析: 已知可推? 除得到等角和直角外,还由角的平分线的性质得到 DE =
DF.求证何来?可证 AD 与 EF 相交所成的四个角中,任意一个为直角.两 者如何联系?可证△DEG≌△DFG(SAS).
解:AD 垂直 EF.理由如下: ∵AD 为△ABC 的角平分线,① ∴∠1 = ∠2 . ∵DE⊥AB 于 E ,DF⊥AC 于 F,② ∴∠AED = ∠AFD =90 ° . ∴Rt△AED 与 Rt△AFD 中, ∠3 = ∠4 . 由①② , 得 DE =DF. 在△DEG 与△DFG 中, (|DE = DF, 〈|l , ∴△DEG≌△DFG(SAS). ∴∠DGE = ∠DGF=90 ° . ∴AD 垂直 EF.
