第六章 反比例函数 单元检测题(含答案)2023-2024学年九年级上册数学北师大版
文档属性
| 名称 | 第六章 反比例函数 单元检测题(含答案)2023-2024学年九年级上册数学北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 351.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 10:22:09 | ||
图片预览

文档简介
第六章《反比例函数》单元检测题
2023-2024学年九年级上册数学北师大版
一、单选题(本大题共12小题,每小题3分,共36分)
1.下列函数中,y是x的反比例函数的是( )
A.x(y﹣1)=1 B.y= C.y=﹣x﹣1 D.y=
2.反比例函数的图象在每个象限内y随x的增大而增大,则k的值可为
A.- 1 B.1 C.-2 D.0
3.学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为平方米的矩形饲养场.设它的一边长为(米),那么另一边的长(米)与(米)的函数图象大致是( )
A. B. C. D.
4.如图,已知△ABO的顶点A和AB边的中点C都在双曲线y=(x>o)的一个分支上,点B在x轴上,CD⊥OB于D,若△AOC的面积为3,则k的值为
A.2 B.3 C.4 D.
5.如图,、是函数的图象上的点,且、关于原点对称,轴于,轴于,如果四边形的面积为,则( ).
A. B. C. D.
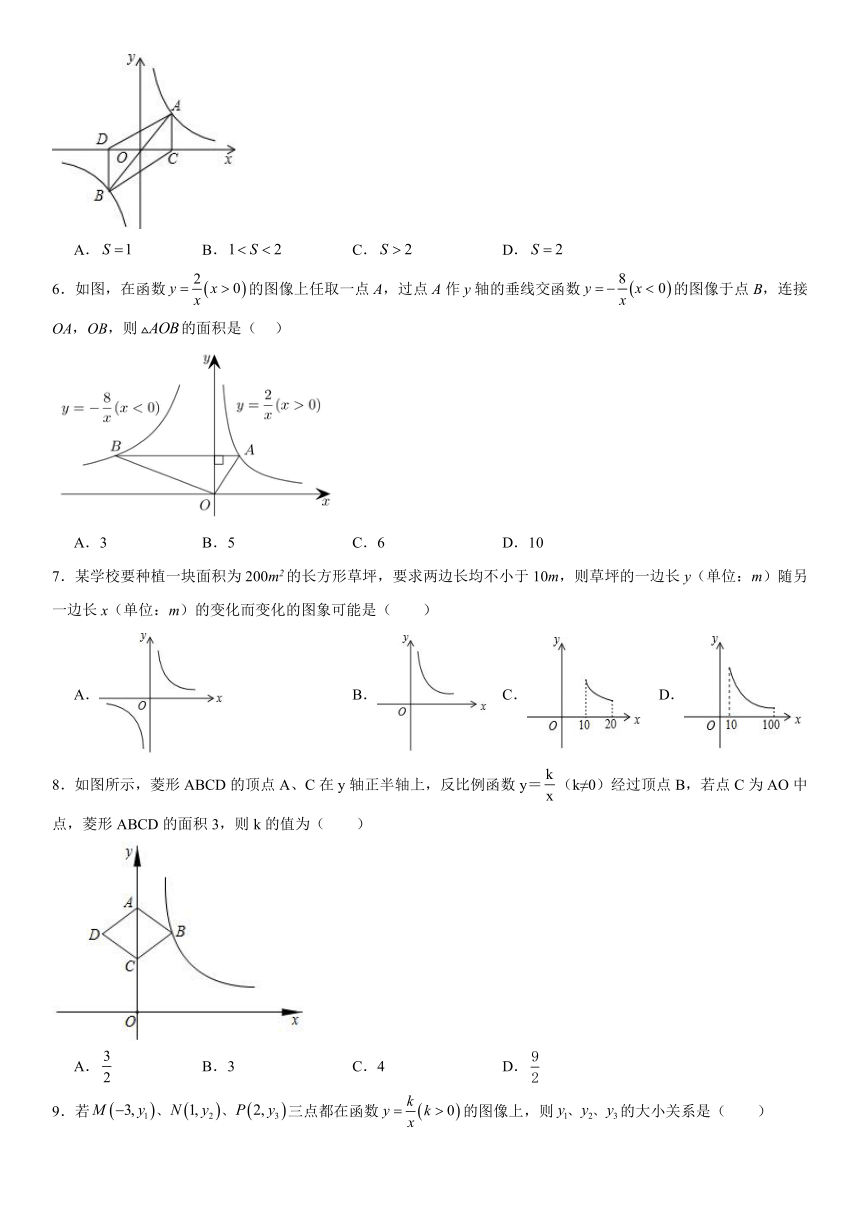
6.如图,在函数的图像上任取一点A,过点A作y轴的垂线交函数的图像于点B,连接OA,OB,则的面积是( )
A.3 B.5 C.6 D.10
7.某学校要种植一块面积为200m2的长方形草坪,要求两边长均不小于10m,则草坪的一边长y(单位:m)随另一边长x(单位:m)的变化而变化的图象可能是( )
A. B. C. D.
8.如图所示,菱形ABCD的顶点A、C在y轴正半轴上,反比例函数y=(k≠0)经过顶点B,若点C为AO中点,菱形ABCD的面积3,则k的值为( )
A. B.3 C.4 D.
9.若三点都在函数的图像上,则的大小关系是( )
A. B. C. D.
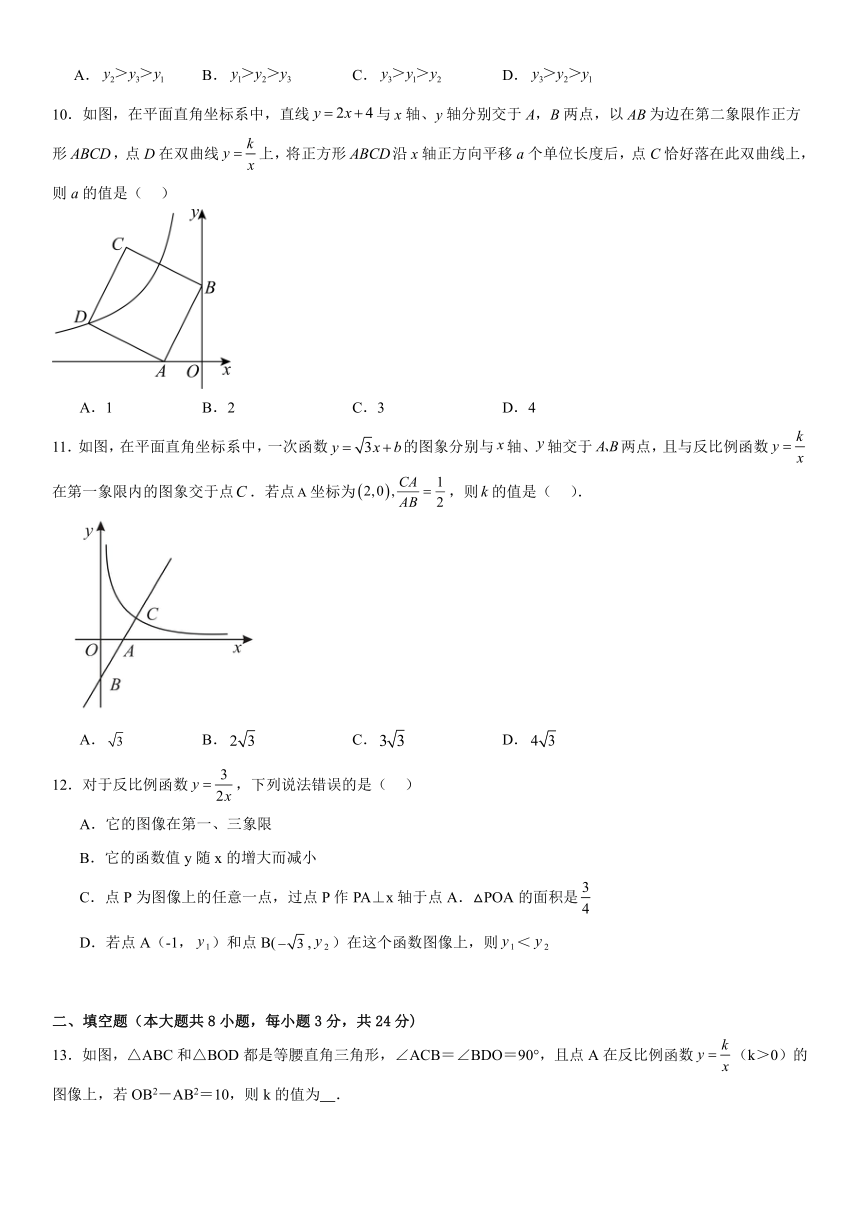
10.如图,在平面直角坐标系中,直线与x轴、y轴分别交于A,B两点,以为边在第二象限作正方形,点D在双曲线上,将正方形沿x轴正方向平移a个单位长度后,点C恰好落在此双曲线上,则a的值是( )
A.1 B.2 C.3 D.4
11.如图,在平面直角坐标系中,一次函数的图象分别与轴、轴交于两点,且与反比例函数在第一象限内的图象交于点.若点坐标为,则的值是( ).
A. B. C. D.
12.对于反比例函数,下列说法错误的是( )
A.它的图像在第一、三象限
B.它的函数值y随x的增大而减小
C.点P为图像上的任意一点,过点P作PA⊥x轴于点A.△POA的面积是
D.若点A(-1,)和点B(,)在这个函数图像上,则<
二、填空题(本大题共8小题,每小题3分,共24分)
13.如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A在反比例函数(k>0)的图像上,若OB2-AB2=10,则k的值为 .
14.设点A(x1,y1)和B(x2,y2)是反比例函数y=图象上的两个点,当x1<x2<0时,y1<y2,则一次函数y=﹣2x+k的图象不经过第 象限.
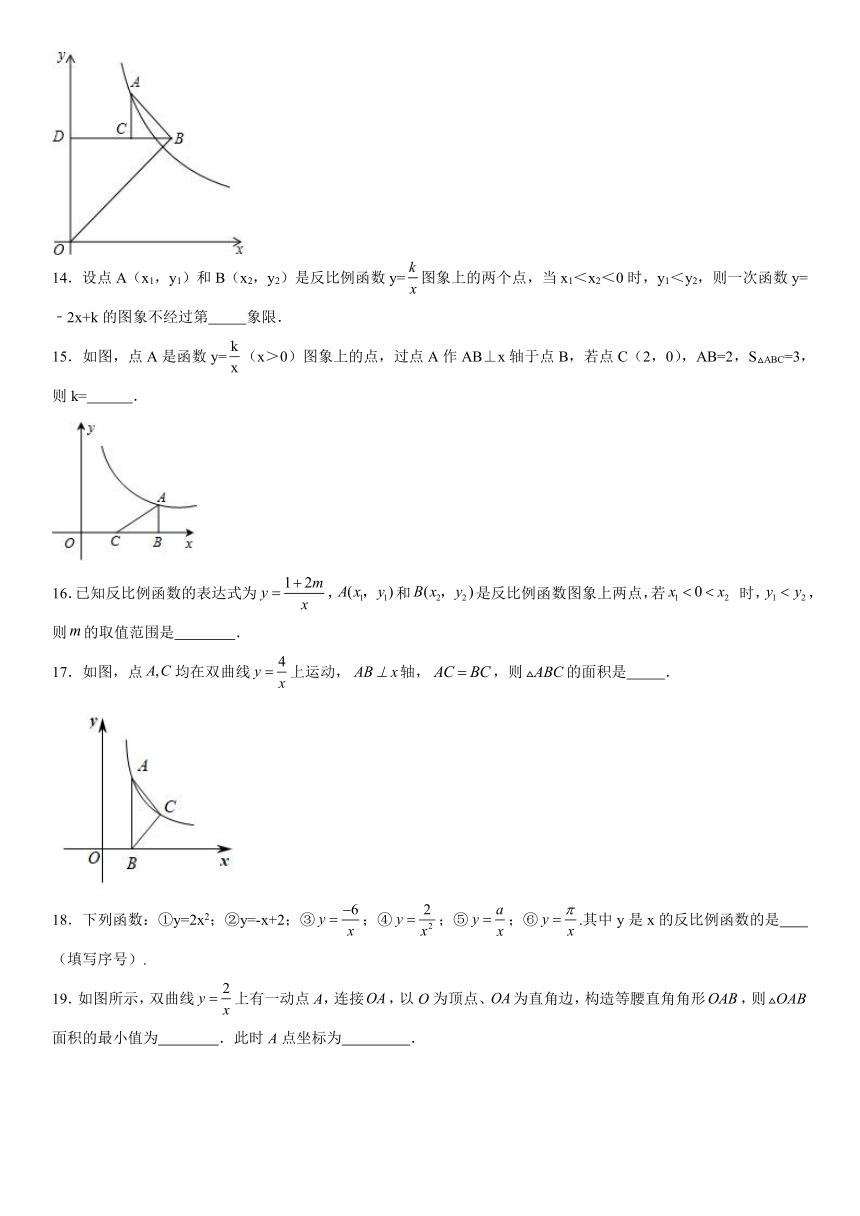
15.如图,点A是函数y=(x>0)图象上的点,过点A作AB⊥x轴于点B,若点C(2,0),AB=2,S△ABC=3,则k= .
16.已知反比例函数的表达式为,和是反比例函数图象上两点,若 时,,则的取值范围是 .
17.如图,点均在双曲线上运动,轴,,则的面积是 .
18.下列函数:①y=2x2;②y=-x+2;③;④;⑤;⑥.其中y是x的反比例函数的是 (填写序号).
19.如图所示,双曲线上有一动点A,连接,以O为顶点、为直角边,构造等腰直角角形,则面积的最小值为 .此时A点坐标为 .
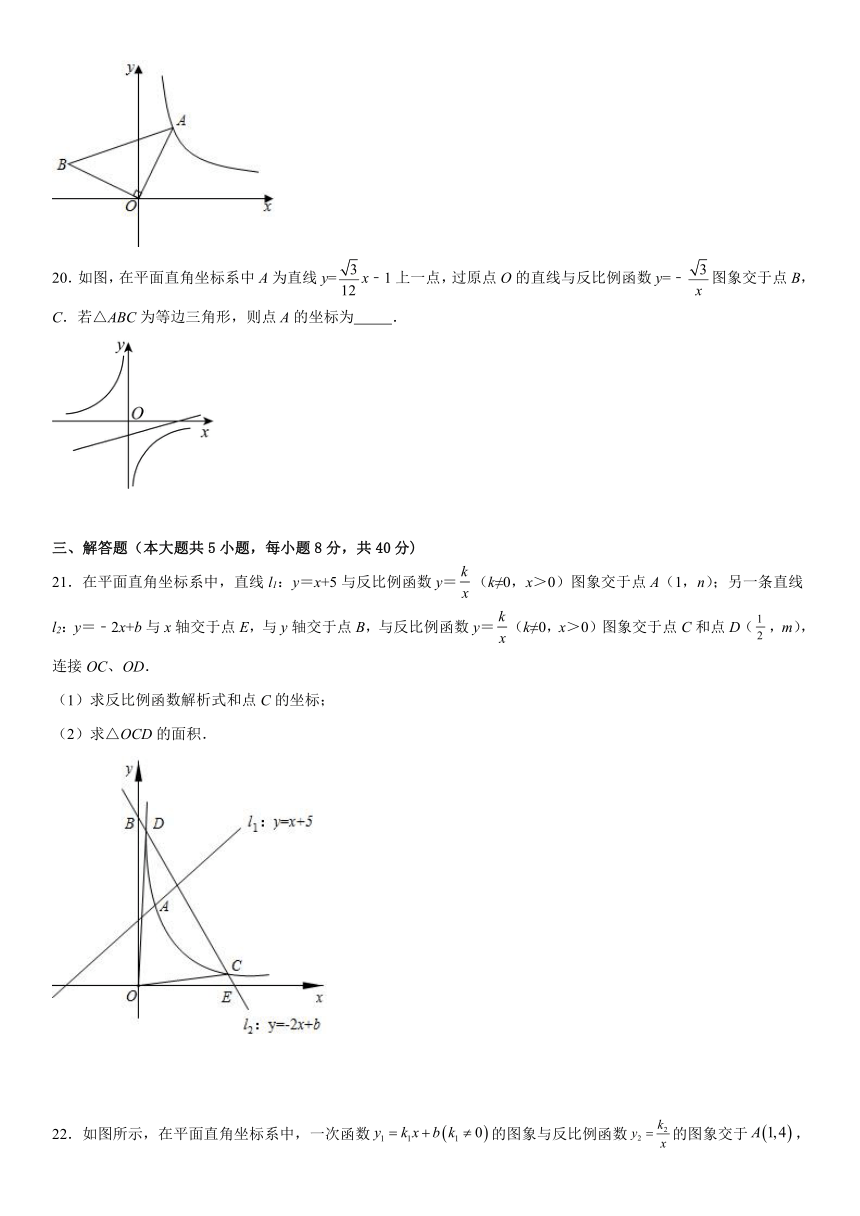
20.如图,在平面直角坐标系中A为直线y=x﹣1上一点,过原点O的直线与反比例函数y=﹣图象交于点B,C.若△ABC为等边三角形,则点A的坐标为 .
三、解答题(本大题共5小题,每小题8分,共40分)
21.在平面直角坐标系中,直线l1:y=x+5与反比例函数y=(k≠0,x>0)图象交于点A(1,n);另一条直线l2:y=﹣2x+b与x轴交于点E,与y轴交于点B,与反比例函数y=(k≠0,x>0)图象交于点C和点D(,m),连接OC、OD.
(1)求反比例函数解析式和点C的坐标;
(2)求△OCD的面积.
22.如图所示,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于,
两点.
(1)求上述反比例函数和一次函数的表达式;
(2)求的面积;
(3)观察图象,写出不等式的解集________.
23.如图,已知一次函数y=ax+b与反比例函数的图象相交于点A(1,3)和B(m,1).
(1)求反比例函数与一次函数的表达式;
(2)根据图象回答,当x取何值时,反比例函数的值大于一次函数的值;
(3)以点O为位似中心画三角形,使它与△OAB位似,且相似比为2,请在图中画出所有符合条件的三角形.
24.如图,直线y=nx+m和双曲线y相交于点A(2,2)和点B(a,﹣1).
(1)求k的值;
(2)求n,m的值;
(3)结合图象写出不等式nx+m的解集: .注:第(3)小题直接写出结果.
25.如图,矩形OABC的顶点A、C分别在、轴的正半轴上,点B点反比例函数(k≠0)的第一象限内的图象上,OA=3,OC=5,动点P在轴的上方,且满足
(1)若点P在这个反比例函数的图象上,求点P的坐标;
(2)连接PO、PA,求PO+PA的最小值;
(3)若点Q在平面内一点,使得以A、B、P、Q为顶点的四边形是菱形,则请你直接写出满足条件的所有点Q的坐标.
参考答案:
1.C
2.C
3.C
4.B
5.D
6.B
7.C
8.D
9.A
10.B
11.C
12.B
13.5.
14.一
15.10
16./m>-0.5
17.2
18.③⑥
19. 2
20.(﹣2,﹣)
21.(1)y=,点C(6,1);(2).
22.(1),
(2)
(3)
23.(1);(2)或
24.(1)4;(2);(3)或
25.(1)P(5,3);(2)最小值为;(3)Q(,8)或(7,8)或(,)或(,)
2023-2024学年九年级上册数学北师大版
一、单选题(本大题共12小题,每小题3分,共36分)
1.下列函数中,y是x的反比例函数的是( )
A.x(y﹣1)=1 B.y= C.y=﹣x﹣1 D.y=
2.反比例函数的图象在每个象限内y随x的增大而增大,则k的值可为
A.- 1 B.1 C.-2 D.0
3.学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为平方米的矩形饲养场.设它的一边长为(米),那么另一边的长(米)与(米)的函数图象大致是( )
A. B. C. D.
4.如图,已知△ABO的顶点A和AB边的中点C都在双曲线y=(x>o)的一个分支上,点B在x轴上,CD⊥OB于D,若△AOC的面积为3,则k的值为
A.2 B.3 C.4 D.
5.如图,、是函数的图象上的点,且、关于原点对称,轴于,轴于,如果四边形的面积为,则( ).
A. B. C. D.
6.如图,在函数的图像上任取一点A,过点A作y轴的垂线交函数的图像于点B,连接OA,OB,则的面积是( )
A.3 B.5 C.6 D.10
7.某学校要种植一块面积为200m2的长方形草坪,要求两边长均不小于10m,则草坪的一边长y(单位:m)随另一边长x(单位:m)的变化而变化的图象可能是( )
A. B. C. D.
8.如图所示,菱形ABCD的顶点A、C在y轴正半轴上,反比例函数y=(k≠0)经过顶点B,若点C为AO中点,菱形ABCD的面积3,则k的值为( )
A. B.3 C.4 D.
9.若三点都在函数的图像上,则的大小关系是( )
A. B. C. D.
10.如图,在平面直角坐标系中,直线与x轴、y轴分别交于A,B两点,以为边在第二象限作正方形,点D在双曲线上,将正方形沿x轴正方向平移a个单位长度后,点C恰好落在此双曲线上,则a的值是( )
A.1 B.2 C.3 D.4
11.如图,在平面直角坐标系中,一次函数的图象分别与轴、轴交于两点,且与反比例函数在第一象限内的图象交于点.若点坐标为,则的值是( ).
A. B. C. D.
12.对于反比例函数,下列说法错误的是( )
A.它的图像在第一、三象限
B.它的函数值y随x的增大而减小
C.点P为图像上的任意一点,过点P作PA⊥x轴于点A.△POA的面积是
D.若点A(-1,)和点B(,)在这个函数图像上,则<
二、填空题(本大题共8小题,每小题3分,共24分)
13.如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A在反比例函数(k>0)的图像上,若OB2-AB2=10,则k的值为 .
14.设点A(x1,y1)和B(x2,y2)是反比例函数y=图象上的两个点,当x1<x2<0时,y1<y2,则一次函数y=﹣2x+k的图象不经过第 象限.
15.如图,点A是函数y=(x>0)图象上的点,过点A作AB⊥x轴于点B,若点C(2,0),AB=2,S△ABC=3,则k= .
16.已知反比例函数的表达式为,和是反比例函数图象上两点,若 时,,则的取值范围是 .
17.如图,点均在双曲线上运动,轴,,则的面积是 .
18.下列函数:①y=2x2;②y=-x+2;③;④;⑤;⑥.其中y是x的反比例函数的是 (填写序号).
19.如图所示,双曲线上有一动点A,连接,以O为顶点、为直角边,构造等腰直角角形,则面积的最小值为 .此时A点坐标为 .
20.如图,在平面直角坐标系中A为直线y=x﹣1上一点,过原点O的直线与反比例函数y=﹣图象交于点B,C.若△ABC为等边三角形,则点A的坐标为 .
三、解答题(本大题共5小题,每小题8分,共40分)
21.在平面直角坐标系中,直线l1:y=x+5与反比例函数y=(k≠0,x>0)图象交于点A(1,n);另一条直线l2:y=﹣2x+b与x轴交于点E,与y轴交于点B,与反比例函数y=(k≠0,x>0)图象交于点C和点D(,m),连接OC、OD.
(1)求反比例函数解析式和点C的坐标;
(2)求△OCD的面积.
22.如图所示,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于,
两点.
(1)求上述反比例函数和一次函数的表达式;
(2)求的面积;
(3)观察图象,写出不等式的解集________.
23.如图,已知一次函数y=ax+b与反比例函数的图象相交于点A(1,3)和B(m,1).
(1)求反比例函数与一次函数的表达式;
(2)根据图象回答,当x取何值时,反比例函数的值大于一次函数的值;
(3)以点O为位似中心画三角形,使它与△OAB位似,且相似比为2,请在图中画出所有符合条件的三角形.
24.如图,直线y=nx+m和双曲线y相交于点A(2,2)和点B(a,﹣1).
(1)求k的值;
(2)求n,m的值;
(3)结合图象写出不等式nx+m的解集: .注:第(3)小题直接写出结果.
25.如图,矩形OABC的顶点A、C分别在、轴的正半轴上,点B点反比例函数(k≠0)的第一象限内的图象上,OA=3,OC=5,动点P在轴的上方,且满足
(1)若点P在这个反比例函数的图象上,求点P的坐标;
(2)连接PO、PA,求PO+PA的最小值;
(3)若点Q在平面内一点,使得以A、B、P、Q为顶点的四边形是菱形,则请你直接写出满足条件的所有点Q的坐标.
参考答案:
1.C
2.C
3.C
4.B
5.D
6.B
7.C
8.D
9.A
10.B
11.C
12.B
13.5.
14.一
15.10
16./m>-0.5
17.2
18.③⑥
19. 2
20.(﹣2,﹣)
21.(1)y=,点C(6,1);(2).
22.(1),
(2)
(3)
23.(1);(2)或
24.(1)4;(2);(3)或
25.(1)P(5,3);(2)最小值为;(3)Q(,8)或(7,8)或(,)或(,)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
