人教版2023年八年级上册 14.2 乘法公式 同步练习卷 (含解析)
文档属性
| 名称 | 人教版2023年八年级上册 14.2 乘法公式 同步练习卷 (含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 214.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 00:00:00 | ||
图片预览



文档简介
人教版2023年八年级上册 14.2 乘法公式 同步练习卷
一.选择题
1.计算(x﹣1)2=( )
A.x2﹣1 B.x2﹣x+1 C.x2﹣2x+1 D.x2+2x+1
2.下列各式能用平方差公式计算的是( )
A.(x﹣y)(y﹣x) B.(﹣m+n)(m﹣n)
C.(2x﹣3)(2x+3) D.(﹣x+2y)(﹣2y+x)
3.若(a+1)(a﹣1)=35,则a的值为( )
A.±6 B.±3 C.6 D.3
4.计算:(a+b﹣c)(a﹣b﹣c)下列步骤出现错误的是( )
①(a﹣c+b)(a﹣c﹣b)
②[(a﹣c)+b][(a﹣c)﹣b]
③(a﹣c)2﹣b2
④a2﹣2ac﹣c2﹣b2
A.① B.② C.③ D.④
5.若多项式4x2+(k﹣1)x+9是关于x的完全平方式,则k的值为( )
A.±13 B.13或﹣11 C.﹣7或﹣5 D.±6
6.若x﹣y=4,xy=5,则x2+y2的值是( )
A.16 B.20 C.25 D.26
7.观察图形,用两种不同的方法计算大长方形面积,我们可以验证等式( )
A.(a+b)(a+2b)=a2+3ab+2b2
B.(a+b)(2a+b)=2a2+3ab+b2
C.(a+b)(a+2b)=2a2+3ab+b2
D.(a+b)(2a+b)=a2+3ab+2b2
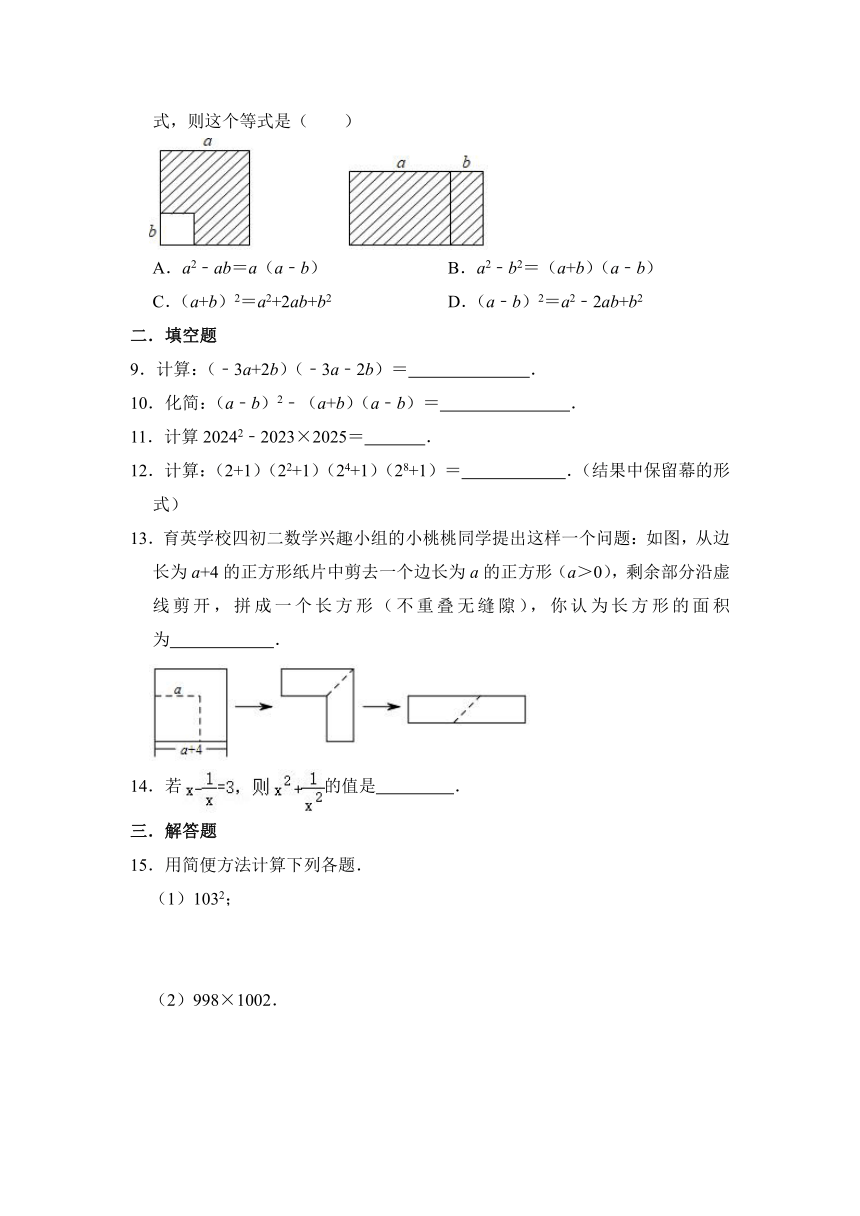
8.在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图),通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
A.a2﹣ab=a(a﹣b) B.a2﹣b2=(a+b)(a﹣b)
C.(a+b)2=a2+2ab+b2 D.(a﹣b)2=a2﹣2ab+b2
二.填空题
9.计算:(﹣3a+2b)(﹣3a﹣2b)= .
10.化简:(a﹣b)2﹣(a+b)(a﹣b)= .
11.计算20242﹣2023×2025= .
12.计算:(2+1)(22+1)(24+1)(28+1)= .(结果中保留幕的形式)
13.育英学校四初二数学兴趣小组的小桃桃同学提出这样一个问题:如图,从边长为a+4的正方形纸片中剪去一个边长为a的正方形(a>0),剩余部分沿虚线剪开,拼成一个长方形(不重叠无缝隙),你认为长方形的面积为 .
14.若的值是 .
三.解答题
15.用简便方法计算下列各题.
(1)1032;
(2)998×1002.
16.先化简,再求值:(2+a)(2﹣a)+(a+3)2,其中a=﹣2.
17.先化简,再求值:(2x+1)2+(x+2)(x﹣2)﹣x(5x﹣4),其中x=2.
18.已知x+y=5,xy=4,求下列各式的值:
(1)x2+y2;
(2)(x﹣y)2.
19.如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
(1)你认为图②中阴影部分的正方形的边长等于 .
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法① .
方法② .
(3)观察图②,试写出(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系 .
(4)根据(3)题中的等量关系,解决如下问题:若a+b=5,ab=2,则求(a﹣b)2的值.
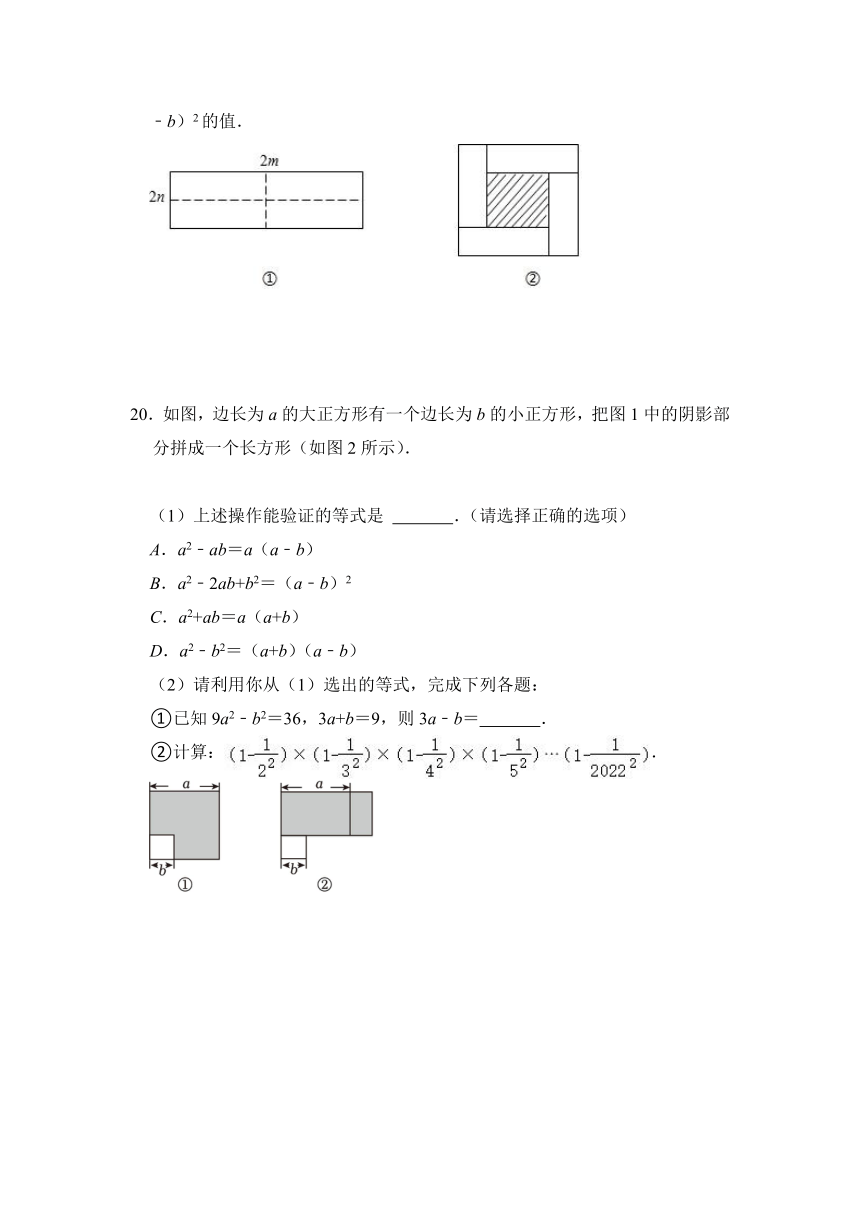
20.如图,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 .(请选择正确的选项)
A.a2﹣ab=a(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
D.a2﹣b2=(a+b)(a﹣b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知9a2﹣b2=36,3a+b=9,则3a﹣b= .
②计算:.
21.阅读材料后解决问题.小明遇到下面一个问题:
计算(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:
(2+1)(22+1)(24+1)(28+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(24﹣1)(28+1)
=216﹣1.
请你根据小明解决问题的方法,试着解决以下的问题:
(1)(2+1)(22+1)(24+1)(28+1)(216+1);
(2)(3+1)(32+1)(34+1)(38+1)(316+1).
试题解析
一.选择题
1.计算(x﹣1)2=( )
A.x2﹣1 B.x2﹣x+1 C.x2﹣2x+1 D.x2+2x+1
【分析】根据完全平方公式求出答案即可.
【解答】解:(x﹣1)2=x2﹣2x+1.
故选:C.
2.下列各式能用平方差公式计算的是( )
A.(x﹣y)(y﹣x) B.(﹣m+n)(m﹣n)
C.(2x﹣3)(2x+3) D.(﹣x+2y)(﹣2y+x)
【分析】利用平方差公式判断即可.
【解答】解:A、原式=﹣(x﹣y)2=﹣x2+2xy﹣y2,不符合题意;
B、原式=﹣(m﹣n)2=﹣m2+2mn﹣n2,不符合题意;
C、原式=4x2﹣9,符合题意;
D、原式=﹣(x﹣2y)2=﹣x2+4xy﹣4y2,不符合题意.
故选:C.
3.若(a+1)(a﹣1)=35,则a的值为( )
A.±6 B.±3 C.6 D.3
【分析】利用平方差公式进行计算,即可解答.
【解答】解:∵(a+1)(a﹣1)=35,
∴a2﹣1=35,
∴a2=36,
∴a=±6,
故选:A.
4.计算:(a+b﹣c)(a﹣b﹣c)下列步骤出现错误的是( )
①(a﹣c+b)(a﹣c﹣b)
②[(a﹣c)+b][(a﹣c)﹣b]
③(a﹣c)2﹣b2
④a2﹣2ac﹣c2﹣b2
A.① B.② C.③ D.④
【分析】运用完全平方公式和平方差公式进行计算、辨别.
【解答】解:∵(a+b﹣c)(a﹣b﹣c)
=(a﹣c+b)(a﹣c﹣b),
=[(a﹣c)+b][(a﹣c)﹣b]
=(a﹣c)2﹣b2
=a2﹣2ac+c2﹣b2,
∴步骤①②③正确,④错误,
故选:D.
5.若多项式4x2+(k﹣1)x+9是关于x的完全平方式,则k的值为( )
A.±13 B.13或﹣11 C.﹣7或﹣5 D.±6
【分析】根据完全平方式得出(k﹣1)x=±2×2x×3,再求出k即可.
【解答】解:∵多项式4x2+(k﹣1)x+9是关于x的完全平方式,
∴(k﹣1)x=±2×2x×3,
∴k=13或﹣11.
故选:B.
6.若x﹣y=4,xy=5,则x2+y2的值是( )
A.16 B.20 C.25 D.26
【分析】根据x﹣y=4得出(x﹣y)2=16,再根据完全平方公式展开即可计算出结果.
【解答】解:∵x﹣y=4,
∴(x﹣y)2=16,
∴x2﹣2xy+y2=16,
∵xy=5,
∴x2+y2=16+2xy=16+2×5=26,
故选:D.
7.观察图形,用两种不同的方法计算大长方形面积,我们可以验证等式( )
A.(a+b)(a+2b)=a2+3ab+2b2
B.(a+b)(2a+b)=2a2+3ab+b2
C.(a+b)(a+2b)=2a2+3ab+b2
D.(a+b)(2a+b)=a2+3ab+2b2
【分析】从“整体”和“部分”两个方面分别用代数式表示大长方形的面积即可.
【解答】解:整体是长为a+2b,宽为a+b的长方形,因此面积为(a+2b)(a+b),
整体是由6个部分的面积和,即a2+3ab+2b2,
因此有(a+2b)(a+b)=a2+3ab+2b2,
故选:A.
8.在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图),通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
A.a2﹣ab=a(a﹣b) B.a2﹣b2=(a+b)(a﹣b)
C.(a+b)2=a2+2ab+b2 D.(a﹣b)2=a2﹣2ab+b2
【分析】这个图形变换可以用来证明平方差公式:已知在左图中,大正方形减小正方形剩下的部分面积为a2﹣b2;因为拼成的长方形的长为(a+b),宽为(a﹣b),根据“长方形的面积=长×宽”代入为:(a+b)×(a﹣b),因为面积相等,进而得出结论.
【解答】解:由图可知,大正方形减小正方形剩下的部分面积为a2﹣b2;
拼成的长方形的面积:(a+b)×(a﹣b),
所以得出:a2﹣b2=(a+b)(a﹣b),
故选:B.
二.填空题
9.计算:(﹣3a+2b)(﹣3a﹣2b)= 9a2﹣4b2 .
【分析】原式利用平方差公式化简即可得到结果.
【解答】解:原式=(﹣3a)2﹣(2b)2=9a2﹣4b2.
故答案为:9a2﹣4b2.
10.化简:(a﹣b)2﹣(a+b)(a﹣b)= ﹣2ab+2b2 .
【分析】根据完全平方公式,平方差公式求解即可.
【解答】解:(a﹣b)2﹣(a+b)(a﹣b)
=a2﹣2ab+b2﹣(a2﹣b2)
=﹣2ab+2b2,
故答案为:﹣2ab+2b2.
11.计算20242﹣2023×2025= 1 .
【分析】将原式变形为20242﹣(2024﹣1)×(2024+1),然后再按平方差公式计算可得答案.
【解答】解:原式=20242﹣(2024﹣1)×(2024+1)
=20242﹣20242+1
=1.
故答案为:1.
12.计算:(2+1)(22+1)(24+1)(28+1)= 216﹣1 .(结果中保留幕的形式)
【分析】将原式变形后利用平方差公式进行计算即可.
【解答】解:(2+1)(22+1)(24+1)(28+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1,
故答案为:216﹣1.
13.育英学校四初二数学兴趣小组的小桃桃同学提出这样一个问题:如图,从边长为a+4的正方形纸片中剪去一个边长为a的正方形(a>0),剩余部分沿虚线剪开,拼成一个长方形(不重叠无缝隙),你认为长方形的面积为 8a+16 .
【分析】根据平方差公式进行计算即可.
【解答】解:拼成的长方形的面积为(a+4)2﹣a2=8a+16,
故答案为:8a+16.
14.若的值是 11 .
【分析】把x﹣=3利用完全平方公式两边平方展开,整理即可得解.
【解答】解:∵x﹣=3,
∴(x﹣)2=9,
即x2﹣2+=9,
解得x2+=9+2=11.
故答案为:11.
三.解答题
15.用简便方法计算下列各题.
(1)1032;
(2)998×1002.
【分析】(1)根据完全平方公式简化运算即可;
(2)根据平方差公式简化运算即可.
【解答】解:(1)1032
=(100+3)2
=1002+2×100×3+32
=10609;
(2)998×1002
=(1000﹣2)×(1000+2)
=1000000﹣4
=999996.
16.先化简,再求值:(2+a)(2﹣a)+(a+3)2,其中a=﹣2.
【分析】用平方差公式和完全平方公式展开,合并同类项后将a=﹣2代入计算即可.
【解答】解:原式=4﹣a2+a2+6a+9
=6a+13;
当a=﹣2时,
原式=6×(﹣2)+13
=﹣12+13
=1.
17.先化简,再求值:(2x+1)2+(x+2)(x﹣2)﹣x(5x﹣4),其中x=2.
【分析】先利用完全平方公式,平方差公式,单项式乘多项式的法则进行计算,然后把x的值代入化简后的式子进行计算,即可解答.
【解答】解:(2x+1)2+(x+2)(x﹣2)﹣x(5x﹣4)
=4x2+4x+1+x2﹣4﹣5x2+4x
=8x﹣3,
当x=2时,原式=8×2﹣3=16﹣3=13.
18.已知x+y=5,xy=4,求下列各式的值:
(1)x2+y2;
(2)(x﹣y)2.
【分析】(1)利用x2+y2=(x+y)2﹣2xy变形,再代入计算;
(2)利用(x﹣y)2=(x+y)2﹣4xy变形,再代入计算;
【解答】解:(1)∵x2+y2=(x+y)2﹣2xy,
∴当x+y=5,xy=4时,
x2+y2=(x+y)2﹣2xy=52﹣2×4=17;
(2)∵(x﹣y)2=(x+y)2﹣4xy,
∴当x+y=5,xy=4时,
(x﹣y)2=(x+y)2﹣4xy=52﹣4×4=9.
19.如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
(1)你认为图②中阴影部分的正方形的边长等于 m﹣n .
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法① (m﹣n)2 .
方法② (m+n)2﹣4mn .
(3)观察图②,试写出(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系 (m﹣n)2=(m+n)2﹣4mn .
(4)根据(3)题中的等量关系,解决如下问题:若a+b=5,ab=2,则求(a﹣b)2的值.
【分析】(1)由拼图可知,图②阴影部分是边长为m﹣n的正方形;
(2)方法一,直接利用正方形的面积公式表示阴影部分的面积;
方法二,从边长为(m+n)的大正方形减去四个长为m,宽为n的矩形面积即可;
(3)由(2)的两种方法求阴影部分的面积可得等式;
(4)将(a﹣b)2的变形为:(a+b)2﹣4ab即可求解.
【解答】解:(1)由拼图可知,阴影部分是边长为(m﹣n)的正方形,
故答案为:m﹣n;
(2)方法一:直接利用正方形的面积公式得正方形的面积为(m﹣n)2;
方法二:从边长为(m+n)的大正方形减去四个长为m,宽为n的矩形面积即为阴影部分的面积,
即(m+n)2﹣4mn;
故答案为:(m﹣n)2,(m+n)2﹣4mn;
(3)由(2)的两种方法可得,(m﹣n)2=(m+n)2﹣4mn;
(4)(a﹣b)2=(a+b)2﹣4ab.
∵a+b=5,ab=2,
∴(a﹣b)2=52﹣4×2=17.
20.如图,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 D .(请选择正确的选项)
A.a2﹣ab=a(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
D.a2﹣b2=(a+b)(a﹣b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知9a2﹣b2=36,3a+b=9,则3a﹣b= 4 .
②计算:.
【分析】(1)用两种方法表示阴影部分的面积即可.
(2)①利用(1)中得到的平方差公式计算即可;②根据平方差公式可进行求解.
【解答】解:(1)图1中阴影部分的面积=a2﹣b2,图②中阴影部分的面积=(a+b)(a﹣b).∴a2﹣b2=(a+b)(a﹣b).
故选:D.
(2)①∵(3a+b)(3a﹣b)=9a2﹣b2,3a+b=9,
∴9(3a﹣b)=36,
∴3a﹣b=36÷9=4.
故答案为:4.
②
=
=
=
=.
21.阅读材料后解决问题.小明遇到下面一个问题:
计算(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:
(2+1)(22+1)(24+1)(28+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(24﹣1)(28+1)
=216﹣1.
请你根据小明解决问题的方法,试着解决以下的问题:
(1)(2+1)(22+1)(24+1)(28+1)(216+1);
(2)(3+1)(32+1)(34+1)(38+1)(316+1).
【分析】(1)根据题中例题可得,在本题式子前面可乘以(2﹣1),然后利用平方差公式即可算出答案;
(2)根据题中例题可得,在整体的式子前面乘以(3﹣1),要想保持结果不变,再在式子前面乘以,然后利用平方差公式即可运算.
【解答】解:(1)原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)(216+1)
=(22﹣1)(22+1)(24+1)(28+1)(216+1)
=(24﹣1)(24+1)(28+1)(216+1)
=(28﹣1)(28+1)(216+1)
=(216﹣1)(216+1)
=232﹣1;
(2)原式=×[(3﹣1)(3+1)(32+1)(34+1)(38+1)(316+1)]
=×[(32﹣1)(32+1)(34+1)(38+1)(316+1)]
=×[(34﹣1)(34+1)(38+1)(316+1)]
=×[(38﹣1)(38+1)(316+1)]
=×[(316﹣1)(316+1)]
=.
一.选择题
1.计算(x﹣1)2=( )
A.x2﹣1 B.x2﹣x+1 C.x2﹣2x+1 D.x2+2x+1
2.下列各式能用平方差公式计算的是( )
A.(x﹣y)(y﹣x) B.(﹣m+n)(m﹣n)
C.(2x﹣3)(2x+3) D.(﹣x+2y)(﹣2y+x)
3.若(a+1)(a﹣1)=35,则a的值为( )
A.±6 B.±3 C.6 D.3
4.计算:(a+b﹣c)(a﹣b﹣c)下列步骤出现错误的是( )
①(a﹣c+b)(a﹣c﹣b)
②[(a﹣c)+b][(a﹣c)﹣b]
③(a﹣c)2﹣b2
④a2﹣2ac﹣c2﹣b2
A.① B.② C.③ D.④
5.若多项式4x2+(k﹣1)x+9是关于x的完全平方式,则k的值为( )
A.±13 B.13或﹣11 C.﹣7或﹣5 D.±6
6.若x﹣y=4,xy=5,则x2+y2的值是( )
A.16 B.20 C.25 D.26
7.观察图形,用两种不同的方法计算大长方形面积,我们可以验证等式( )
A.(a+b)(a+2b)=a2+3ab+2b2
B.(a+b)(2a+b)=2a2+3ab+b2
C.(a+b)(a+2b)=2a2+3ab+b2
D.(a+b)(2a+b)=a2+3ab+2b2
8.在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图),通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
A.a2﹣ab=a(a﹣b) B.a2﹣b2=(a+b)(a﹣b)
C.(a+b)2=a2+2ab+b2 D.(a﹣b)2=a2﹣2ab+b2
二.填空题
9.计算:(﹣3a+2b)(﹣3a﹣2b)= .
10.化简:(a﹣b)2﹣(a+b)(a﹣b)= .
11.计算20242﹣2023×2025= .
12.计算:(2+1)(22+1)(24+1)(28+1)= .(结果中保留幕的形式)
13.育英学校四初二数学兴趣小组的小桃桃同学提出这样一个问题:如图,从边长为a+4的正方形纸片中剪去一个边长为a的正方形(a>0),剩余部分沿虚线剪开,拼成一个长方形(不重叠无缝隙),你认为长方形的面积为 .
14.若的值是 .
三.解答题
15.用简便方法计算下列各题.
(1)1032;
(2)998×1002.
16.先化简,再求值:(2+a)(2﹣a)+(a+3)2,其中a=﹣2.
17.先化简,再求值:(2x+1)2+(x+2)(x﹣2)﹣x(5x﹣4),其中x=2.
18.已知x+y=5,xy=4,求下列各式的值:
(1)x2+y2;
(2)(x﹣y)2.
19.如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
(1)你认为图②中阴影部分的正方形的边长等于 .
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法① .
方法② .
(3)观察图②,试写出(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系 .
(4)根据(3)题中的等量关系,解决如下问题:若a+b=5,ab=2,则求(a﹣b)2的值.
20.如图,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 .(请选择正确的选项)
A.a2﹣ab=a(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
D.a2﹣b2=(a+b)(a﹣b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知9a2﹣b2=36,3a+b=9,则3a﹣b= .
②计算:.
21.阅读材料后解决问题.小明遇到下面一个问题:
计算(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:
(2+1)(22+1)(24+1)(28+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(24﹣1)(28+1)
=216﹣1.
请你根据小明解决问题的方法,试着解决以下的问题:
(1)(2+1)(22+1)(24+1)(28+1)(216+1);
(2)(3+1)(32+1)(34+1)(38+1)(316+1).
试题解析
一.选择题
1.计算(x﹣1)2=( )
A.x2﹣1 B.x2﹣x+1 C.x2﹣2x+1 D.x2+2x+1
【分析】根据完全平方公式求出答案即可.
【解答】解:(x﹣1)2=x2﹣2x+1.
故选:C.
2.下列各式能用平方差公式计算的是( )
A.(x﹣y)(y﹣x) B.(﹣m+n)(m﹣n)
C.(2x﹣3)(2x+3) D.(﹣x+2y)(﹣2y+x)
【分析】利用平方差公式判断即可.
【解答】解:A、原式=﹣(x﹣y)2=﹣x2+2xy﹣y2,不符合题意;
B、原式=﹣(m﹣n)2=﹣m2+2mn﹣n2,不符合题意;
C、原式=4x2﹣9,符合题意;
D、原式=﹣(x﹣2y)2=﹣x2+4xy﹣4y2,不符合题意.
故选:C.
3.若(a+1)(a﹣1)=35,则a的值为( )
A.±6 B.±3 C.6 D.3
【分析】利用平方差公式进行计算,即可解答.
【解答】解:∵(a+1)(a﹣1)=35,
∴a2﹣1=35,
∴a2=36,
∴a=±6,
故选:A.
4.计算:(a+b﹣c)(a﹣b﹣c)下列步骤出现错误的是( )
①(a﹣c+b)(a﹣c﹣b)
②[(a﹣c)+b][(a﹣c)﹣b]
③(a﹣c)2﹣b2
④a2﹣2ac﹣c2﹣b2
A.① B.② C.③ D.④
【分析】运用完全平方公式和平方差公式进行计算、辨别.
【解答】解:∵(a+b﹣c)(a﹣b﹣c)
=(a﹣c+b)(a﹣c﹣b),
=[(a﹣c)+b][(a﹣c)﹣b]
=(a﹣c)2﹣b2
=a2﹣2ac+c2﹣b2,
∴步骤①②③正确,④错误,
故选:D.
5.若多项式4x2+(k﹣1)x+9是关于x的完全平方式,则k的值为( )
A.±13 B.13或﹣11 C.﹣7或﹣5 D.±6
【分析】根据完全平方式得出(k﹣1)x=±2×2x×3,再求出k即可.
【解答】解:∵多项式4x2+(k﹣1)x+9是关于x的完全平方式,
∴(k﹣1)x=±2×2x×3,
∴k=13或﹣11.
故选:B.
6.若x﹣y=4,xy=5,则x2+y2的值是( )
A.16 B.20 C.25 D.26
【分析】根据x﹣y=4得出(x﹣y)2=16,再根据完全平方公式展开即可计算出结果.
【解答】解:∵x﹣y=4,
∴(x﹣y)2=16,
∴x2﹣2xy+y2=16,
∵xy=5,
∴x2+y2=16+2xy=16+2×5=26,
故选:D.
7.观察图形,用两种不同的方法计算大长方形面积,我们可以验证等式( )
A.(a+b)(a+2b)=a2+3ab+2b2
B.(a+b)(2a+b)=2a2+3ab+b2
C.(a+b)(a+2b)=2a2+3ab+b2
D.(a+b)(2a+b)=a2+3ab+2b2
【分析】从“整体”和“部分”两个方面分别用代数式表示大长方形的面积即可.
【解答】解:整体是长为a+2b,宽为a+b的长方形,因此面积为(a+2b)(a+b),
整体是由6个部分的面积和,即a2+3ab+2b2,
因此有(a+2b)(a+b)=a2+3ab+2b2,
故选:A.
8.在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图),通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
A.a2﹣ab=a(a﹣b) B.a2﹣b2=(a+b)(a﹣b)
C.(a+b)2=a2+2ab+b2 D.(a﹣b)2=a2﹣2ab+b2
【分析】这个图形变换可以用来证明平方差公式:已知在左图中,大正方形减小正方形剩下的部分面积为a2﹣b2;因为拼成的长方形的长为(a+b),宽为(a﹣b),根据“长方形的面积=长×宽”代入为:(a+b)×(a﹣b),因为面积相等,进而得出结论.
【解答】解:由图可知,大正方形减小正方形剩下的部分面积为a2﹣b2;
拼成的长方形的面积:(a+b)×(a﹣b),
所以得出:a2﹣b2=(a+b)(a﹣b),
故选:B.
二.填空题
9.计算:(﹣3a+2b)(﹣3a﹣2b)= 9a2﹣4b2 .
【分析】原式利用平方差公式化简即可得到结果.
【解答】解:原式=(﹣3a)2﹣(2b)2=9a2﹣4b2.
故答案为:9a2﹣4b2.
10.化简:(a﹣b)2﹣(a+b)(a﹣b)= ﹣2ab+2b2 .
【分析】根据完全平方公式,平方差公式求解即可.
【解答】解:(a﹣b)2﹣(a+b)(a﹣b)
=a2﹣2ab+b2﹣(a2﹣b2)
=﹣2ab+2b2,
故答案为:﹣2ab+2b2.
11.计算20242﹣2023×2025= 1 .
【分析】将原式变形为20242﹣(2024﹣1)×(2024+1),然后再按平方差公式计算可得答案.
【解答】解:原式=20242﹣(2024﹣1)×(2024+1)
=20242﹣20242+1
=1.
故答案为:1.
12.计算:(2+1)(22+1)(24+1)(28+1)= 216﹣1 .(结果中保留幕的形式)
【分析】将原式变形后利用平方差公式进行计算即可.
【解答】解:(2+1)(22+1)(24+1)(28+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1,
故答案为:216﹣1.
13.育英学校四初二数学兴趣小组的小桃桃同学提出这样一个问题:如图,从边长为a+4的正方形纸片中剪去一个边长为a的正方形(a>0),剩余部分沿虚线剪开,拼成一个长方形(不重叠无缝隙),你认为长方形的面积为 8a+16 .
【分析】根据平方差公式进行计算即可.
【解答】解:拼成的长方形的面积为(a+4)2﹣a2=8a+16,
故答案为:8a+16.
14.若的值是 11 .
【分析】把x﹣=3利用完全平方公式两边平方展开,整理即可得解.
【解答】解:∵x﹣=3,
∴(x﹣)2=9,
即x2﹣2+=9,
解得x2+=9+2=11.
故答案为:11.
三.解答题
15.用简便方法计算下列各题.
(1)1032;
(2)998×1002.
【分析】(1)根据完全平方公式简化运算即可;
(2)根据平方差公式简化运算即可.
【解答】解:(1)1032
=(100+3)2
=1002+2×100×3+32
=10609;
(2)998×1002
=(1000﹣2)×(1000+2)
=1000000﹣4
=999996.
16.先化简,再求值:(2+a)(2﹣a)+(a+3)2,其中a=﹣2.
【分析】用平方差公式和完全平方公式展开,合并同类项后将a=﹣2代入计算即可.
【解答】解:原式=4﹣a2+a2+6a+9
=6a+13;
当a=﹣2时,
原式=6×(﹣2)+13
=﹣12+13
=1.
17.先化简,再求值:(2x+1)2+(x+2)(x﹣2)﹣x(5x﹣4),其中x=2.
【分析】先利用完全平方公式,平方差公式,单项式乘多项式的法则进行计算,然后把x的值代入化简后的式子进行计算,即可解答.
【解答】解:(2x+1)2+(x+2)(x﹣2)﹣x(5x﹣4)
=4x2+4x+1+x2﹣4﹣5x2+4x
=8x﹣3,
当x=2时,原式=8×2﹣3=16﹣3=13.
18.已知x+y=5,xy=4,求下列各式的值:
(1)x2+y2;
(2)(x﹣y)2.
【分析】(1)利用x2+y2=(x+y)2﹣2xy变形,再代入计算;
(2)利用(x﹣y)2=(x+y)2﹣4xy变形,再代入计算;
【解答】解:(1)∵x2+y2=(x+y)2﹣2xy,
∴当x+y=5,xy=4时,
x2+y2=(x+y)2﹣2xy=52﹣2×4=17;
(2)∵(x﹣y)2=(x+y)2﹣4xy,
∴当x+y=5,xy=4时,
(x﹣y)2=(x+y)2﹣4xy=52﹣4×4=9.
19.如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
(1)你认为图②中阴影部分的正方形的边长等于 m﹣n .
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法① (m﹣n)2 .
方法② (m+n)2﹣4mn .
(3)观察图②,试写出(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系 (m﹣n)2=(m+n)2﹣4mn .
(4)根据(3)题中的等量关系,解决如下问题:若a+b=5,ab=2,则求(a﹣b)2的值.
【分析】(1)由拼图可知,图②阴影部分是边长为m﹣n的正方形;
(2)方法一,直接利用正方形的面积公式表示阴影部分的面积;
方法二,从边长为(m+n)的大正方形减去四个长为m,宽为n的矩形面积即可;
(3)由(2)的两种方法求阴影部分的面积可得等式;
(4)将(a﹣b)2的变形为:(a+b)2﹣4ab即可求解.
【解答】解:(1)由拼图可知,阴影部分是边长为(m﹣n)的正方形,
故答案为:m﹣n;
(2)方法一:直接利用正方形的面积公式得正方形的面积为(m﹣n)2;
方法二:从边长为(m+n)的大正方形减去四个长为m,宽为n的矩形面积即为阴影部分的面积,
即(m+n)2﹣4mn;
故答案为:(m﹣n)2,(m+n)2﹣4mn;
(3)由(2)的两种方法可得,(m﹣n)2=(m+n)2﹣4mn;
(4)(a﹣b)2=(a+b)2﹣4ab.
∵a+b=5,ab=2,
∴(a﹣b)2=52﹣4×2=17.
20.如图,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 D .(请选择正确的选项)
A.a2﹣ab=a(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
D.a2﹣b2=(a+b)(a﹣b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知9a2﹣b2=36,3a+b=9,则3a﹣b= 4 .
②计算:.
【分析】(1)用两种方法表示阴影部分的面积即可.
(2)①利用(1)中得到的平方差公式计算即可;②根据平方差公式可进行求解.
【解答】解:(1)图1中阴影部分的面积=a2﹣b2,图②中阴影部分的面积=(a+b)(a﹣b).∴a2﹣b2=(a+b)(a﹣b).
故选:D.
(2)①∵(3a+b)(3a﹣b)=9a2﹣b2,3a+b=9,
∴9(3a﹣b)=36,
∴3a﹣b=36÷9=4.
故答案为:4.
②
=
=
=
=.
21.阅读材料后解决问题.小明遇到下面一个问题:
计算(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:
(2+1)(22+1)(24+1)(28+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(24﹣1)(28+1)
=216﹣1.
请你根据小明解决问题的方法,试着解决以下的问题:
(1)(2+1)(22+1)(24+1)(28+1)(216+1);
(2)(3+1)(32+1)(34+1)(38+1)(316+1).
【分析】(1)根据题中例题可得,在本题式子前面可乘以(2﹣1),然后利用平方差公式即可算出答案;
(2)根据题中例题可得,在整体的式子前面乘以(3﹣1),要想保持结果不变,再在式子前面乘以,然后利用平方差公式即可运算.
【解答】解:(1)原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)(216+1)
=(22﹣1)(22+1)(24+1)(28+1)(216+1)
=(24﹣1)(24+1)(28+1)(216+1)
=(28﹣1)(28+1)(216+1)
=(216﹣1)(216+1)
=232﹣1;
(2)原式=×[(3﹣1)(3+1)(32+1)(34+1)(38+1)(316+1)]
=×[(32﹣1)(32+1)(34+1)(38+1)(316+1)]
=×[(34﹣1)(34+1)(38+1)(316+1)]
=×[(38﹣1)(38+1)(316+1)]
=×[(316﹣1)(316+1)]
=.
