安徽省淮北市第二中学2023-2024学年八年级上学期期中数学试题(沪科版)(无答案)
文档属性
| 名称 | 安徽省淮北市第二中学2023-2024学年八年级上学期期中数学试题(沪科版)(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 343.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 10:28:53 | ||
图片预览

文档简介
数学八年级(沪科版)·教学评价二(期中)
(2023—2024学年上学期 评价范围:11~13章)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在平面直角坐标系中,点所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列函数①,②,③,④,⑤中,是一次函数的有( )
A.1个 B.2个 C.3个 D.4个
3.下列每组数分别表示三根木棒的长,将木棒首尾连接后,能摆成三角形的一组是( )
A.1,3,1 B.2,2,4 C.3,4,5 D.1,2,3
4.关于函数,下列结论正确的是( )
A.图像必经过点 B.图像经过第一、二、三象限
C.y随x的增大而增大 D.图像与直线平行
5.如图,将三角尺的直角顶点放在直尺的一边上,若,,则的度数等于( )
第5题图
A.20° B.30° C.40° D.50°
6.下列命题中,属于假命题的是( )
A.如果a,b都是正数,那么
B.如果,那么
C.如果一个三角形是直角三角形,那么它的两个锐角互余
D.同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行
7.已知一次函数的图像经过点,且当时,,则该函数图像所经过的象限为( )
A.一、二、三 B.二、三、四 C.一、三、四 D.一、二、四
8.小亮每天从家去学校上学行走的路程为900米,某天他从家去上学时以每分钟30米的速度行走了前半程,为了不迟到他加快了速度,以每分钟45米的速度行走完了剩下的路程,那么小亮行走的路程y(米)与他行走的时间t(分钟)()之间的函数表达式是( )
A. B.
C. D.
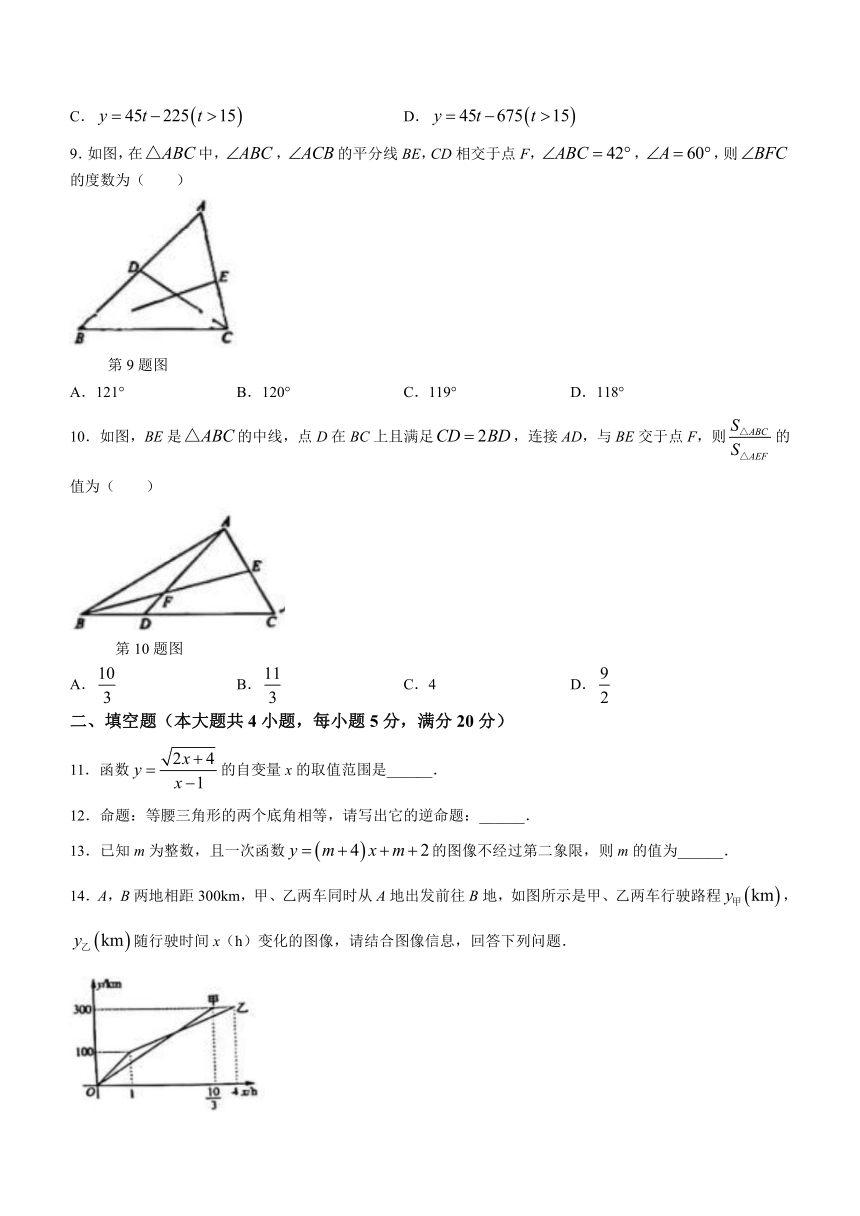
9.如图,在中,,的平分线BE,CD相交于点F,,,则的度数为( )
第9题图
A.121° B.120° C.119° D.118°
10.如图,BE是的中线,点D在BC上且满足,连接AD,与BE交于点F,则的值为( )
第10题图
A. B. C.4 D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.函数的自变量x的取值范围是______.
12.命题:等腰三角形的两个底角相等,请写出它的逆命题:______.
13.已知m为整数,且一次函数的图像不经过第二象限,则m的值为______.
14.A,B两地相距300km,甲、乙两车同时从A地出发前往B地,如图所示是甲、乙两车行驶路程,随行驶时间x(h)变化的图像,请结合图像信息,回答下列问题.
第14题图
(1)甲车的速度为______km/h;
(2)当甲、乙两车相距10km时,乙车行驶的时间为______h.
三、(本大题共2小题,每小题8分,满分16分)
15.已知点是平面直角坐标系上的点.
(1)若点P是第二象限的角平分线上一点,求点P的坐标;
(2)若点P在第一象限,且到两坐标轴的距离之和为9,求点P的坐标.
16.在平面直角坐标系中,若点,,在同一条直线上,求a的值.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在中,点D在BC上,且,,,求和的度数.
第17题图
18.如图,在正方形网格中有一个格点三角形ABC(的各顶点都在格点上).
第18题图
(1)画出中AB边上的高CD;
(2)将先向上平移3格,再向右平移4格,画出平移后的;
(3)在图中画出一个锐角格点三角形ABP,使得其面积等于的面积,并回答满足条件的点P有多少个.
五、(本大题共2小题,每小题10分,满分20分)
19.已知的三边长分别为a,b,c.
(1)若a,b,c满足,试判断的形状;
(2)若,,且c为整数,求的周长的最大值及最小值.
20.如图,在平面直角坐标系中,直线l:与直线交于点A,已知点A的横
坐标为.
第20题图
(1)求k的值;
(2)求两直线与x轴围成的三角形面积.
六、(本题满分12分)
21.为了鼓励大家节约用电,某电力公司采取按月用电量分段收费,居民每月应交电费y(元)与用电量x(度)的函数图像是一条折线(如图所示),根据图像解答下列问题:
第21题图
(1)求出y与x的函数关系式;
(2)若某用户某月用电80度,则应缴电费多少元?
(3)若某用户某月应缴电费105元,则该用户用了多少度电?
七、(本题满分12分)
22.在中,AE平分,.
第22题图1 第22题图2 第22题图3
(1)如图1,若于点D,,,则______;
(2)如图2,若点P是线段AE上一动点,过点P作于点G,则与,之间的数量关系是______;
(3)如图3,若点P是AE延长线上一点,过点P作于点G,则与,之间有何数量关系?画出图形并证明你的结论.
八、(本题满分14分)
23.2023年暑假,多地发生水灾,某企业组织了20辆货车装运甲、乙、丙三种共120吨救援物资前往灾区,按计划20辆货车都要装运,每辆货车只能装运同一种物资且必须装满.已知每辆货车单独装甲种物资可装8吨,单独装乙种物资可装6吨,单独装丙种物资可装5吨.
(1)设装运甲种物资的车辆数为x辆,装运乙种物资的车辆数为y辆,求y与x之间的函数关系式;
(2)如果装运每种物资的车辆都不少于3辆,那么车辆的安排方案有哪几种?
(3)若购买甲种物资需每吨3万元,乙种物资每吨4万元,丙种物资每吨2万元,在(2)的条件下,该公司此次购买捐赠物资至少花费多少万元?
(2023—2024学年上学期 评价范围:11~13章)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在平面直角坐标系中,点所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列函数①,②,③,④,⑤中,是一次函数的有( )
A.1个 B.2个 C.3个 D.4个
3.下列每组数分别表示三根木棒的长,将木棒首尾连接后,能摆成三角形的一组是( )
A.1,3,1 B.2,2,4 C.3,4,5 D.1,2,3
4.关于函数,下列结论正确的是( )
A.图像必经过点 B.图像经过第一、二、三象限
C.y随x的增大而增大 D.图像与直线平行
5.如图,将三角尺的直角顶点放在直尺的一边上,若,,则的度数等于( )
第5题图
A.20° B.30° C.40° D.50°
6.下列命题中,属于假命题的是( )
A.如果a,b都是正数,那么
B.如果,那么
C.如果一个三角形是直角三角形,那么它的两个锐角互余
D.同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行
7.已知一次函数的图像经过点,且当时,,则该函数图像所经过的象限为( )
A.一、二、三 B.二、三、四 C.一、三、四 D.一、二、四
8.小亮每天从家去学校上学行走的路程为900米,某天他从家去上学时以每分钟30米的速度行走了前半程,为了不迟到他加快了速度,以每分钟45米的速度行走完了剩下的路程,那么小亮行走的路程y(米)与他行走的时间t(分钟)()之间的函数表达式是( )
A. B.
C. D.
9.如图,在中,,的平分线BE,CD相交于点F,,,则的度数为( )
第9题图
A.121° B.120° C.119° D.118°
10.如图,BE是的中线,点D在BC上且满足,连接AD,与BE交于点F,则的值为( )
第10题图
A. B. C.4 D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.函数的自变量x的取值范围是______.
12.命题:等腰三角形的两个底角相等,请写出它的逆命题:______.
13.已知m为整数,且一次函数的图像不经过第二象限,则m的值为______.
14.A,B两地相距300km,甲、乙两车同时从A地出发前往B地,如图所示是甲、乙两车行驶路程,随行驶时间x(h)变化的图像,请结合图像信息,回答下列问题.
第14题图
(1)甲车的速度为______km/h;
(2)当甲、乙两车相距10km时,乙车行驶的时间为______h.
三、(本大题共2小题,每小题8分,满分16分)
15.已知点是平面直角坐标系上的点.
(1)若点P是第二象限的角平分线上一点,求点P的坐标;
(2)若点P在第一象限,且到两坐标轴的距离之和为9,求点P的坐标.
16.在平面直角坐标系中,若点,,在同一条直线上,求a的值.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在中,点D在BC上,且,,,求和的度数.
第17题图
18.如图,在正方形网格中有一个格点三角形ABC(的各顶点都在格点上).
第18题图
(1)画出中AB边上的高CD;
(2)将先向上平移3格,再向右平移4格,画出平移后的;
(3)在图中画出一个锐角格点三角形ABP,使得其面积等于的面积,并回答满足条件的点P有多少个.
五、(本大题共2小题,每小题10分,满分20分)
19.已知的三边长分别为a,b,c.
(1)若a,b,c满足,试判断的形状;
(2)若,,且c为整数,求的周长的最大值及最小值.
20.如图,在平面直角坐标系中,直线l:与直线交于点A,已知点A的横
坐标为.
第20题图
(1)求k的值;
(2)求两直线与x轴围成的三角形面积.
六、(本题满分12分)
21.为了鼓励大家节约用电,某电力公司采取按月用电量分段收费,居民每月应交电费y(元)与用电量x(度)的函数图像是一条折线(如图所示),根据图像解答下列问题:
第21题图
(1)求出y与x的函数关系式;
(2)若某用户某月用电80度,则应缴电费多少元?
(3)若某用户某月应缴电费105元,则该用户用了多少度电?
七、(本题满分12分)
22.在中,AE平分,.
第22题图1 第22题图2 第22题图3
(1)如图1,若于点D,,,则______;
(2)如图2,若点P是线段AE上一动点,过点P作于点G,则与,之间的数量关系是______;
(3)如图3,若点P是AE延长线上一点,过点P作于点G,则与,之间有何数量关系?画出图形并证明你的结论.
八、(本题满分14分)
23.2023年暑假,多地发生水灾,某企业组织了20辆货车装运甲、乙、丙三种共120吨救援物资前往灾区,按计划20辆货车都要装运,每辆货车只能装运同一种物资且必须装满.已知每辆货车单独装甲种物资可装8吨,单独装乙种物资可装6吨,单独装丙种物资可装5吨.
(1)设装运甲种物资的车辆数为x辆,装运乙种物资的车辆数为y辆,求y与x之间的函数关系式;
(2)如果装运每种物资的车辆都不少于3辆,那么车辆的安排方案有哪几种?
(3)若购买甲种物资需每吨3万元,乙种物资每吨4万元,丙种物资每吨2万元,在(2)的条件下,该公司此次购买捐赠物资至少花费多少万元?
同课章节目录
