5.2 平面直角坐标系(第3课时)(同步课件)(30张ppt)-2023-2024学年八年级数学上册同步精品课堂(苏科版)
文档属性
| 名称 | 5.2 平面直角坐标系(第3课时)(同步课件)(30张ppt)-2023-2024学年八年级数学上册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 00:00:00 | ||
图片预览





文档简介
(共30张PPT)
第5章 · 平面直角坐标系
5.2 平面直角坐标系(3)
第3课时 建立坐标系描述点的位置
学习目标
1. 在同一直角坐标系中,探索位置变化与数量变化的关系、图形位置的变化与点的坐标变化的关系;
2. 能建立适当的平面直角坐标系,将实际问题数学化,并会用平面直角坐标系解决问题;
3. 进一步感受数形结合的数学思想.
思考与探索
你知道视频中的机械手是如何工作的吗
如果你是工程师,那么你怎样向机械手下达指令,让它能把元器件准确插入相应的孔眼中?
需要提供“地址”.
思考与探索
O
y
x
a
d
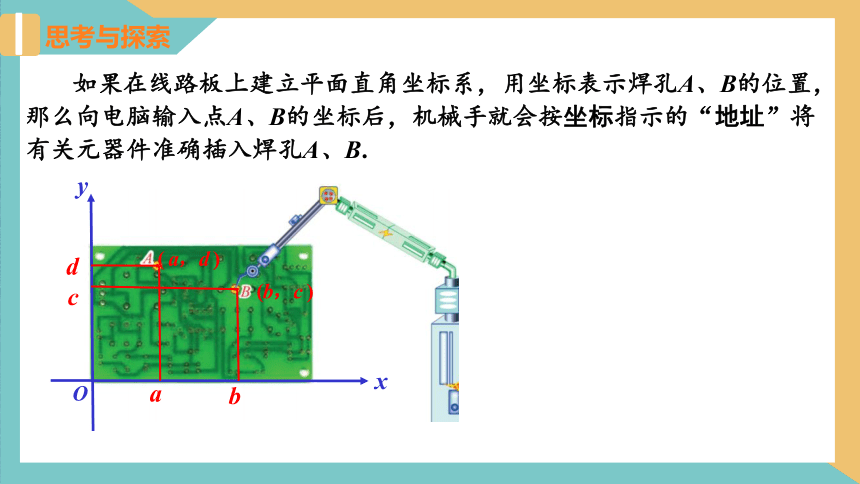
如果在线路板上建立平面直角坐标系,用坐标表示焊孔A、B的位置,那么向电脑输入点A、B的坐标后,机械手就会按坐标指示的“地址”将有关元器件准确插入焊孔A、B.
b
c
( a,d )
(b,c )
尝试与交流
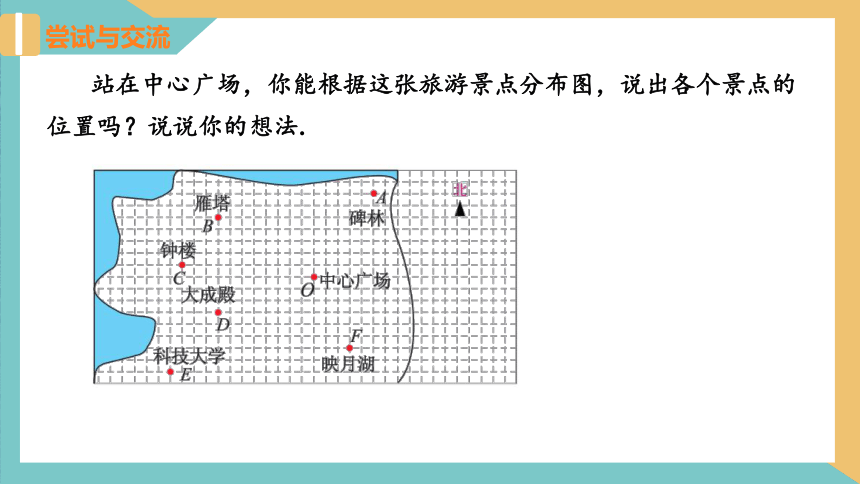
站在中心广场,你能根据这张旅游景点分布图,说出各个景点的位置吗?说说你的想法.
尝试与交流
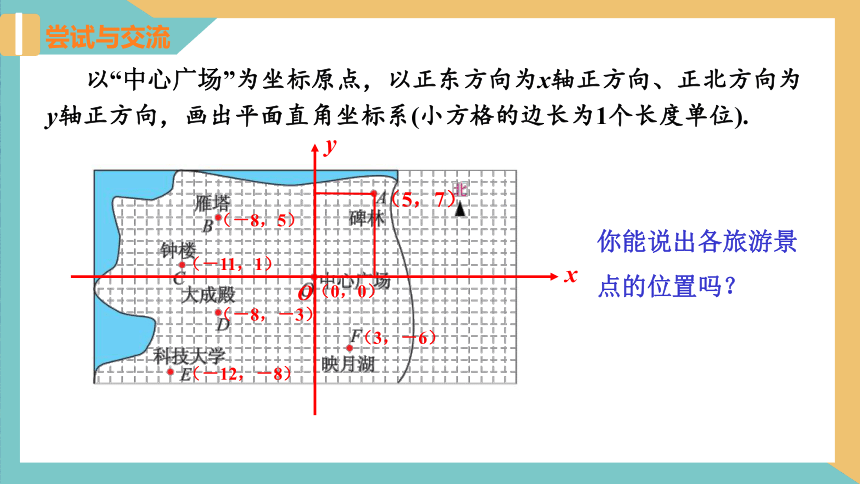
以“中心广场”为坐标原点,以正东方向为x轴正方向、正北方向为y轴正方向,画出平面直角坐标系(小方格的边长为1个长度单位).
你能说出各旅游景点的位置吗?
O
y
x
(0,0)
(5,7)
(-8,5)
(-11,1)
(-8,-3)
(-12,-8)
(3,-6)
尝试与交流
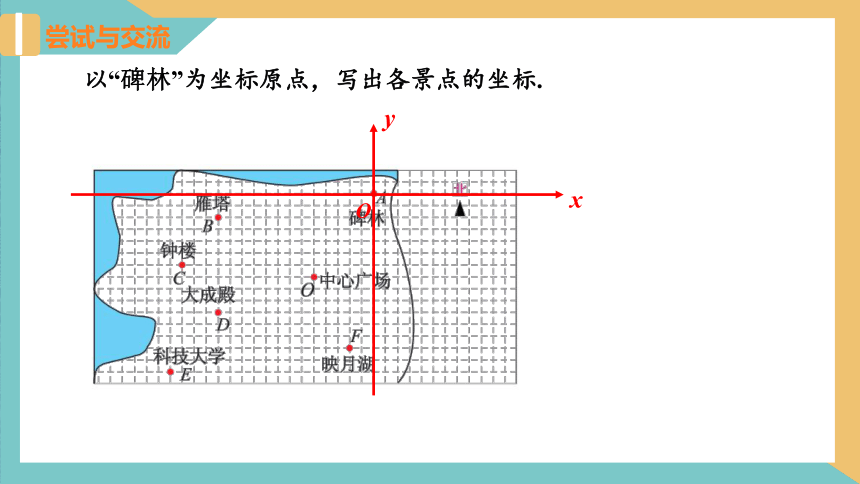
以“碑林”为坐标原点,写出各景点的坐标.
O
y
x
尝试与交流
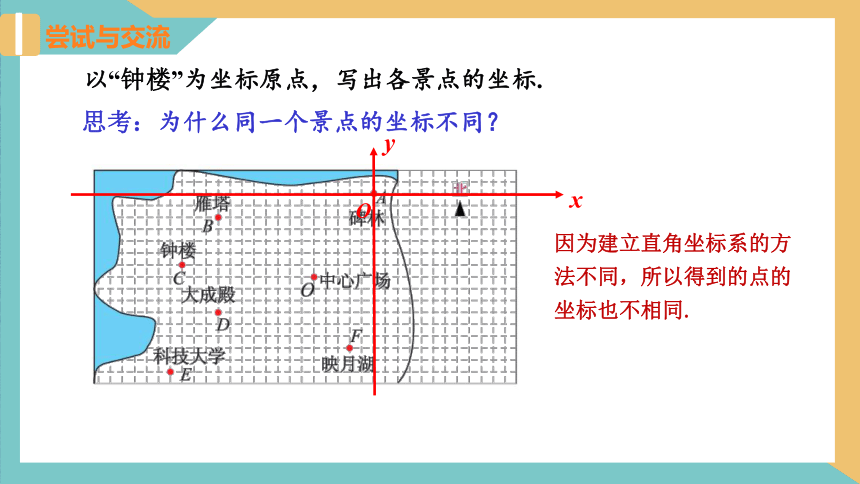
以“钟楼”为坐标原点,写出各景点的坐标.
O
y
x
思考:为什么同一个景点的坐标不同?
因为建立直角坐标系的方法不同,所以得到的点的坐标也不相同.
A
B
C
D
例题讲解
3
1
4
2
O
1
2
3
4
5
y
x
5
6
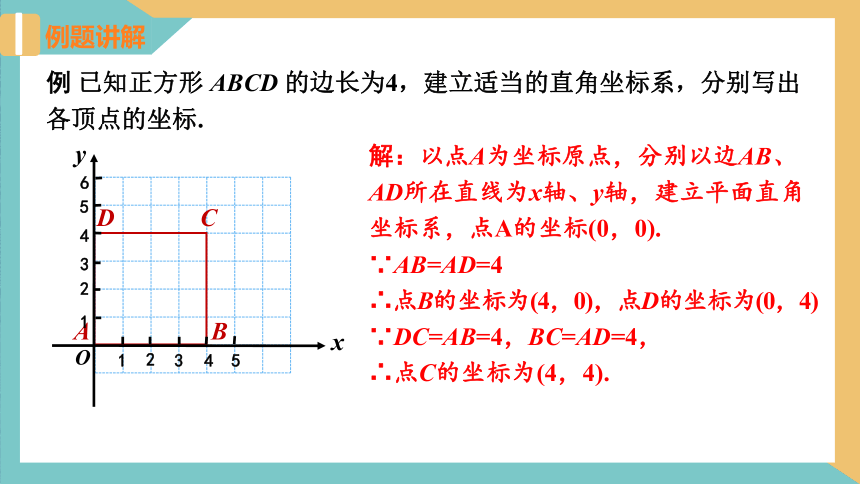
例 已知正方形 ABCD 的边长为4,建立适当的直角坐标系,分别写出各顶点的坐标.
解:以点A为坐标原点,分别以边AB、
AD所在直线为x轴、y轴,建立平面直角
坐标系,点A的坐标(0,0).
∵AB=AD=4
∴点B的坐标为(4,0),点D的坐标为(0,4)
∵DC=AB=4,BC=AD=4,
∴点C的坐标为(4,4).
3
1
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
-5
A
B
C
D
讨论交流
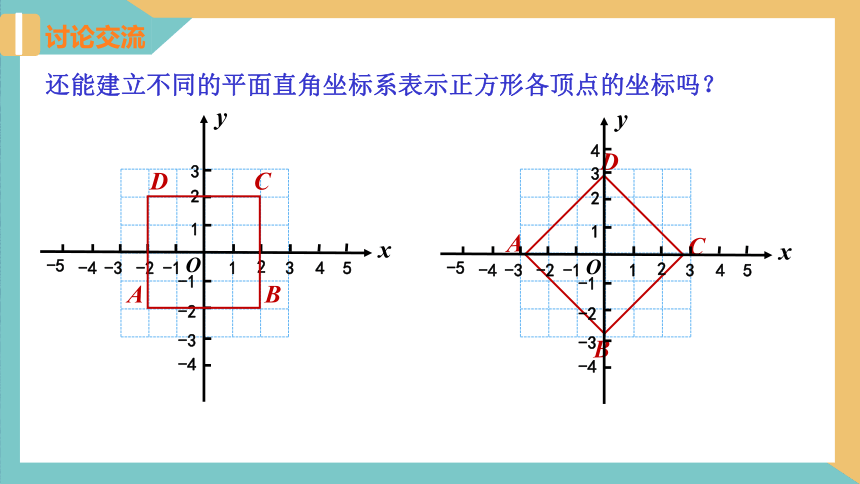
还能建立不同的平面直角坐标系表示正方形各顶点的坐标吗?
A
B
C
D
3
1
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
-5
4
归纳总结
(3)标出正方向与单位长度;
建立直角坐标系描述点的位置一般步骤:
(1)分析条件,选择适当的点作为原点;
(2)过原点在两个垂直的方向上分别作出x轴与y轴;
(4)求出各点的坐标.
(4)以某个已知点为原点建立平面直角坐标系.
归纳总结
如何建立直角坐标系较为合适?
建立平面直角坐标系的常见方法:
(2)以某些特殊的线段所在的直线为x轴或y轴(如高线、等腰三角形底边上的中线等);
(3)以轴对称图形的对称轴为x轴或y轴;
(1)使图形中尽量多的点在坐标轴上;
1. 根据某动物园的平面示意图,以大门所在的位置为坐标原点,以正东方向为轴正方向、正北方向为轴正方向,以1cm为单位长度,建立平面直角坐标系,用坐标表示猴山、驼峰、百鸟园和熊猫馆的位置:
新知巩固
O
5
6
7
8
9
1
2
3
4
x
5
3
4
1
2
y
新知巩固
2. 在△PAB 中,PA=PB,AB=2.建立适当的平面直角坐标系,分别写出△PAB是等边三角形、等腰直角三角形时各顶点的坐标.
P
A
B
y
x
O
P
A
B
y
P
A
B
新知巩固
2. 在△PAB 中,PA=PB,AB=2.建立适当的平面直角坐标系,分别写出△PAB是等边三角形、等腰直角三角形时各顶点的坐标.
x
y
O
P
A
B
y
新知巩固
3.某校八年级(1)班周日组织学生春游,参观了如图所示的一些景点和设施,为了便于确定位置,带队老师在图中建立了平面直角坐标系(横轴和纵轴均为小正方形的边所在直线,每个小正方形的边长均为1个单位长度).
(2,-2)
(-3,2)
x
y
(1)若带队老师建立的平面直角坐标系中,游乐园的坐标为(2,-2),湖心亭的坐标为(-3,2),请你在图中画出这个平面直角坐标系;
(2)根据(1)中建立的平面直角坐标系,指出其他景点的坐标.
解:(1)如图所示.
(2)其他景点的坐标分别为音乐台(0,4),望春亭(-2,-1),牡丹园(3,3),文艺馆(0,0).
课堂小结
建立坐标系描述点的位置
根据已知点的坐标确定物体的位置
建立适当的直角坐标系确定几何图形中点的坐标
当堂检测
1. 在平面内有A,B两点,若以点B为原点建立平面直角坐标系,则点A的坐标为(2,3);若以点A为原点建立平面直角坐标系(两平面直角坐标系x轴、y轴方向一致),则点B的坐标是( )
A.(-2,-3) B.(-2,3) C.(2,-3) D.(2,3)
A
2. 有一个边长为4的正方形,在建立平面直角坐标系后,三个顶点的坐标分别为(1,1),(-3,1),(-3,5),则第四个顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
A
当堂检测
3. 如图是某动物园的示意图,若分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,表示狮虎山的点的坐标为( 0,1 ),表示熊猫馆的点的坐标为( 2.5,-0.5 ),则表示百鸟园的点的坐标为( )
A.( -2,-1 ) B.( -1,-2 )
C.( 2,-1 ) D.( -1,2 )
A
y
x
O
当堂检测
4.天水历史悠久,文物古迹星罗棋布,是中国历史文化名城,也是中国优秀旅游城市.如图是秦州区的部分旅游景点,请你以中心广场为坐标原点建立平面直角坐标系,并写出各景点的坐标:
城隍庙:___________;
胡氏民居:_________;
泰山庙:___________;
玉泉观:___________;
伏羲庙:___________;
李广墓:___________.
O
y
x
(4,0)
(1,0)
(3,3)
(-3,3)
(-6,-1)
(2,-4)
5.数学课上,王老师让同学们对给定的正方形ABCD,如图.建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
甲同学:A(0,1),B(0,0),C(1,0),D(1,1);
乙同学:A(0,0),B(0,-1),C(1,-1),D(1,0);
丙同学:A(1,0),B(1,-2),C(3,-2),D(3,0);
丁同学:A(-1,2),B(-1,0),C(0,0),D(0,2);
上述四名同学表示的结果中,四个点的坐标都表示正确的同学是__________.
甲、乙、丙
C
D
A
B
当堂检测
当堂检测
6. 如图为某公园的示意图.
(1)以虎山为原点,水平向右为x轴正方向、铅直向上为y轴正方向在图中建立平面直角坐标系,并写出各景点的坐标;
解:如图,建立平面直角坐标系.
虎山(0,0),熊猫馆(3,2),
鸟岛(-1,3),狮子馆(-2,-2),猴园(3,-1).
y
x
O
当堂检测
(2)以猴园为原点,水平向右为x轴正方向、铅直向上为y轴正方向建立平面直角坐标系,并写出各景点坐标;
y
x
O
解:如图,建立平面直角坐标系.
虎山(-3,1),熊猫馆(0,3),
鸟岛(-4,4),狮子馆(-5,-1),猴园(0,0).
当堂检测
(3)比较两个平面直角坐标系下各景点的坐标,你发现了什么规律?
解:与(1)中各景点的坐标相比,(2)中各景点的坐标横坐标减小3,纵坐标增加1.
当堂检测
7. 如图,已知长方形ABCD的长为6,宽为4,请建立适当的平面直角坐标系,分别表示其各个顶点的坐标.
C
D
A
B
解:如图,以长方形ABCD两相邻边所在的直线为坐标轴,建立平面直角坐标系,则A(0,4),B(0,0),C(6,0),D(6,4).
x
y
当堂检测
7. 如图,已知长方形ABCD的长为6,宽为4,请建立适当的平面直角坐标系,分别表示其各个顶点的坐标.
C
D
A
B
x
y
O
C
D
A
B
x
y
O
思维提升
①当表示政府广场的点的坐标为(0,0),表示庐江汽车站的点的坐标为(﹣2,﹣3)时,表示周瑜文化园的点的坐标为(6,﹣4);②当表示政府广场的点的坐标为(0,0),表示庐江汽车站的点的坐标为(﹣4,﹣6)时,表示周瑜文化园的点的坐标为(12,﹣8);③当表示政府广场的点的坐标为(1,1),表示庐江汽车站的点的坐标为(﹣3,﹣5)时,表示周瑜文化园的点的坐标为(13,﹣7);④当表示政府广场的点的坐标为(1.5,1.5)表示庐江汽车站的点的坐标为(﹣4.5,﹣7.5)时,表示周瑜文化园的点的坐标为(19.5,﹣10.5).
上述结论中,所有正确结论的序号是_______________.
①②③④
8. 如图是庐城一些地点的分布示意图.在图中,分别以向右,向上为x轴,y轴的正方向建立平面直角坐标系,有如下四个结论:
思维提升
9.如图,菱形ABCD的边长为6,∠ABC=45°.
(1)试建立适当的平面直角坐标系表示该菱形并写出其各顶点的坐标.
C
D
A
B
x
y
O
E
解:以点为坐标原点,菱形BC的所在的直线为x轴,BC所在直线的垂线为y轴建立平面直角坐标系,如图,
过点A作于点,
∵菱形的边长为6,,
∵ ,
∴ ,
∴,,
∵,
∴,,,.
思维提升
(2)若要计算该菱形的面积,你有什么办法?
C
D
A
B
x
y
O
E
(2)∵,,,
∴S菱形
.
第5章 · 平面直角坐标系
5.2 平面直角坐标系(3)
第3课时 建立坐标系描述点的位置
学习目标
1. 在同一直角坐标系中,探索位置变化与数量变化的关系、图形位置的变化与点的坐标变化的关系;
2. 能建立适当的平面直角坐标系,将实际问题数学化,并会用平面直角坐标系解决问题;
3. 进一步感受数形结合的数学思想.
思考与探索
你知道视频中的机械手是如何工作的吗
如果你是工程师,那么你怎样向机械手下达指令,让它能把元器件准确插入相应的孔眼中?
需要提供“地址”.
思考与探索
O
y
x
a
d
如果在线路板上建立平面直角坐标系,用坐标表示焊孔A、B的位置,那么向电脑输入点A、B的坐标后,机械手就会按坐标指示的“地址”将有关元器件准确插入焊孔A、B.
b
c
( a,d )
(b,c )
尝试与交流
站在中心广场,你能根据这张旅游景点分布图,说出各个景点的位置吗?说说你的想法.
尝试与交流
以“中心广场”为坐标原点,以正东方向为x轴正方向、正北方向为y轴正方向,画出平面直角坐标系(小方格的边长为1个长度单位).
你能说出各旅游景点的位置吗?
O
y
x
(0,0)
(5,7)
(-8,5)
(-11,1)
(-8,-3)
(-12,-8)
(3,-6)
尝试与交流
以“碑林”为坐标原点,写出各景点的坐标.
O
y
x
尝试与交流
以“钟楼”为坐标原点,写出各景点的坐标.
O
y
x
思考:为什么同一个景点的坐标不同?
因为建立直角坐标系的方法不同,所以得到的点的坐标也不相同.
A
B
C
D
例题讲解
3
1
4
2
O
1
2
3
4
5
y
x
5
6
例 已知正方形 ABCD 的边长为4,建立适当的直角坐标系,分别写出各顶点的坐标.
解:以点A为坐标原点,分别以边AB、
AD所在直线为x轴、y轴,建立平面直角
坐标系,点A的坐标(0,0).
∵AB=AD=4
∴点B的坐标为(4,0),点D的坐标为(0,4)
∵DC=AB=4,BC=AD=4,
∴点C的坐标为(4,4).
3
1
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
-5
A
B
C
D
讨论交流
还能建立不同的平面直角坐标系表示正方形各顶点的坐标吗?
A
B
C
D
3
1
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
-5
4
归纳总结
(3)标出正方向与单位长度;
建立直角坐标系描述点的位置一般步骤:
(1)分析条件,选择适当的点作为原点;
(2)过原点在两个垂直的方向上分别作出x轴与y轴;
(4)求出各点的坐标.
(4)以某个已知点为原点建立平面直角坐标系.
归纳总结
如何建立直角坐标系较为合适?
建立平面直角坐标系的常见方法:
(2)以某些特殊的线段所在的直线为x轴或y轴(如高线、等腰三角形底边上的中线等);
(3)以轴对称图形的对称轴为x轴或y轴;
(1)使图形中尽量多的点在坐标轴上;
1. 根据某动物园的平面示意图,以大门所在的位置为坐标原点,以正东方向为轴正方向、正北方向为轴正方向,以1cm为单位长度,建立平面直角坐标系,用坐标表示猴山、驼峰、百鸟园和熊猫馆的位置:
新知巩固
O
5
6
7
8
9
1
2
3
4
x
5
3
4
1
2
y
新知巩固
2. 在△PAB 中,PA=PB,AB=2.建立适当的平面直角坐标系,分别写出△PAB是等边三角形、等腰直角三角形时各顶点的坐标.
P
A
B
y
x
O
P
A
B
y
P
A
B
新知巩固
2. 在△PAB 中,PA=PB,AB=2.建立适当的平面直角坐标系,分别写出△PAB是等边三角形、等腰直角三角形时各顶点的坐标.
x
y
O
P
A
B
y
新知巩固
3.某校八年级(1)班周日组织学生春游,参观了如图所示的一些景点和设施,为了便于确定位置,带队老师在图中建立了平面直角坐标系(横轴和纵轴均为小正方形的边所在直线,每个小正方形的边长均为1个单位长度).
(2,-2)
(-3,2)
x
y
(1)若带队老师建立的平面直角坐标系中,游乐园的坐标为(2,-2),湖心亭的坐标为(-3,2),请你在图中画出这个平面直角坐标系;
(2)根据(1)中建立的平面直角坐标系,指出其他景点的坐标.
解:(1)如图所示.
(2)其他景点的坐标分别为音乐台(0,4),望春亭(-2,-1),牡丹园(3,3),文艺馆(0,0).
课堂小结
建立坐标系描述点的位置
根据已知点的坐标确定物体的位置
建立适当的直角坐标系确定几何图形中点的坐标
当堂检测
1. 在平面内有A,B两点,若以点B为原点建立平面直角坐标系,则点A的坐标为(2,3);若以点A为原点建立平面直角坐标系(两平面直角坐标系x轴、y轴方向一致),则点B的坐标是( )
A.(-2,-3) B.(-2,3) C.(2,-3) D.(2,3)
A
2. 有一个边长为4的正方形,在建立平面直角坐标系后,三个顶点的坐标分别为(1,1),(-3,1),(-3,5),则第四个顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
A
当堂检测
3. 如图是某动物园的示意图,若分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,表示狮虎山的点的坐标为( 0,1 ),表示熊猫馆的点的坐标为( 2.5,-0.5 ),则表示百鸟园的点的坐标为( )
A.( -2,-1 ) B.( -1,-2 )
C.( 2,-1 ) D.( -1,2 )
A
y
x
O
当堂检测
4.天水历史悠久,文物古迹星罗棋布,是中国历史文化名城,也是中国优秀旅游城市.如图是秦州区的部分旅游景点,请你以中心广场为坐标原点建立平面直角坐标系,并写出各景点的坐标:
城隍庙:___________;
胡氏民居:_________;
泰山庙:___________;
玉泉观:___________;
伏羲庙:___________;
李广墓:___________.
O
y
x
(4,0)
(1,0)
(3,3)
(-3,3)
(-6,-1)
(2,-4)
5.数学课上,王老师让同学们对给定的正方形ABCD,如图.建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
甲同学:A(0,1),B(0,0),C(1,0),D(1,1);
乙同学:A(0,0),B(0,-1),C(1,-1),D(1,0);
丙同学:A(1,0),B(1,-2),C(3,-2),D(3,0);
丁同学:A(-1,2),B(-1,0),C(0,0),D(0,2);
上述四名同学表示的结果中,四个点的坐标都表示正确的同学是__________.
甲、乙、丙
C
D
A
B
当堂检测
当堂检测
6. 如图为某公园的示意图.
(1)以虎山为原点,水平向右为x轴正方向、铅直向上为y轴正方向在图中建立平面直角坐标系,并写出各景点的坐标;
解:如图,建立平面直角坐标系.
虎山(0,0),熊猫馆(3,2),
鸟岛(-1,3),狮子馆(-2,-2),猴园(3,-1).
y
x
O
当堂检测
(2)以猴园为原点,水平向右为x轴正方向、铅直向上为y轴正方向建立平面直角坐标系,并写出各景点坐标;
y
x
O
解:如图,建立平面直角坐标系.
虎山(-3,1),熊猫馆(0,3),
鸟岛(-4,4),狮子馆(-5,-1),猴园(0,0).
当堂检测
(3)比较两个平面直角坐标系下各景点的坐标,你发现了什么规律?
解:与(1)中各景点的坐标相比,(2)中各景点的坐标横坐标减小3,纵坐标增加1.
当堂检测
7. 如图,已知长方形ABCD的长为6,宽为4,请建立适当的平面直角坐标系,分别表示其各个顶点的坐标.
C
D
A
B
解:如图,以长方形ABCD两相邻边所在的直线为坐标轴,建立平面直角坐标系,则A(0,4),B(0,0),C(6,0),D(6,4).
x
y
当堂检测
7. 如图,已知长方形ABCD的长为6,宽为4,请建立适当的平面直角坐标系,分别表示其各个顶点的坐标.
C
D
A
B
x
y
O
C
D
A
B
x
y
O
思维提升
①当表示政府广场的点的坐标为(0,0),表示庐江汽车站的点的坐标为(﹣2,﹣3)时,表示周瑜文化园的点的坐标为(6,﹣4);②当表示政府广场的点的坐标为(0,0),表示庐江汽车站的点的坐标为(﹣4,﹣6)时,表示周瑜文化园的点的坐标为(12,﹣8);③当表示政府广场的点的坐标为(1,1),表示庐江汽车站的点的坐标为(﹣3,﹣5)时,表示周瑜文化园的点的坐标为(13,﹣7);④当表示政府广场的点的坐标为(1.5,1.5)表示庐江汽车站的点的坐标为(﹣4.5,﹣7.5)时,表示周瑜文化园的点的坐标为(19.5,﹣10.5).
上述结论中,所有正确结论的序号是_______________.
①②③④
8. 如图是庐城一些地点的分布示意图.在图中,分别以向右,向上为x轴,y轴的正方向建立平面直角坐标系,有如下四个结论:
思维提升
9.如图,菱形ABCD的边长为6,∠ABC=45°.
(1)试建立适当的平面直角坐标系表示该菱形并写出其各顶点的坐标.
C
D
A
B
x
y
O
E
解:以点为坐标原点,菱形BC的所在的直线为x轴,BC所在直线的垂线为y轴建立平面直角坐标系,如图,
过点A作于点,
∵菱形的边长为6,,
∵ ,
∴ ,
∴,,
∵,
∴,,,.
思维提升
(2)若要计算该菱形的面积,你有什么办法?
C
D
A
B
x
y
O
E
(2)∵,,,
∴S菱形
.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
