6.3.3 数据的表示(第3课时)课件(共29张PPT)-2023-2024学年七年级数学上册同步精品课堂(北师大版)
文档属性
| 名称 | 6.3.3 数据的表示(第3课时)课件(共29张PPT)-2023-2024学年七年级数学上册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 832.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
新课标 北师大版
七年级上册
6.3.3数据的表示(第3课时)
第六章
数据的收集与整理
学习目标
1.明确频数直方图制作的步骤,会绘制频数直方图。
2.能从频数分布表和频数直方图中获取有关信息,作出合理的判断和预测。
新课引入
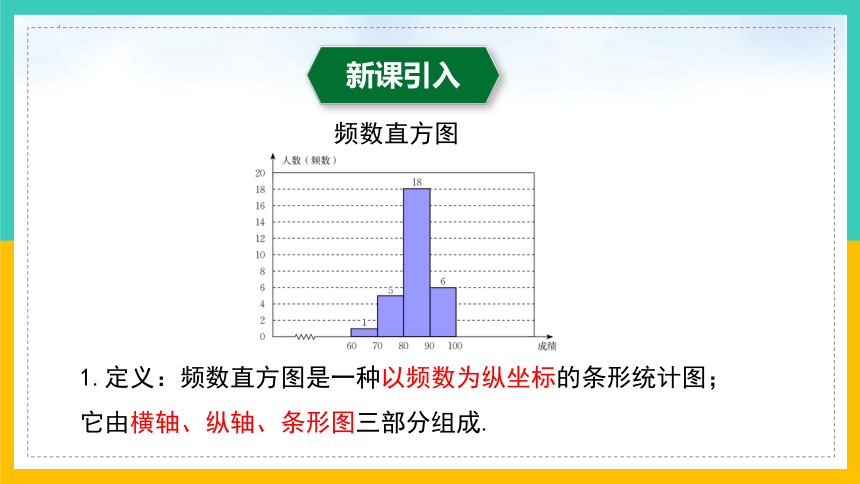
1.定义:频数直方图是一种以频数为纵坐标的条形统计图;
它由横轴、纵轴、条形图三部分组成.
频数直方图
新课引入
频数直方图
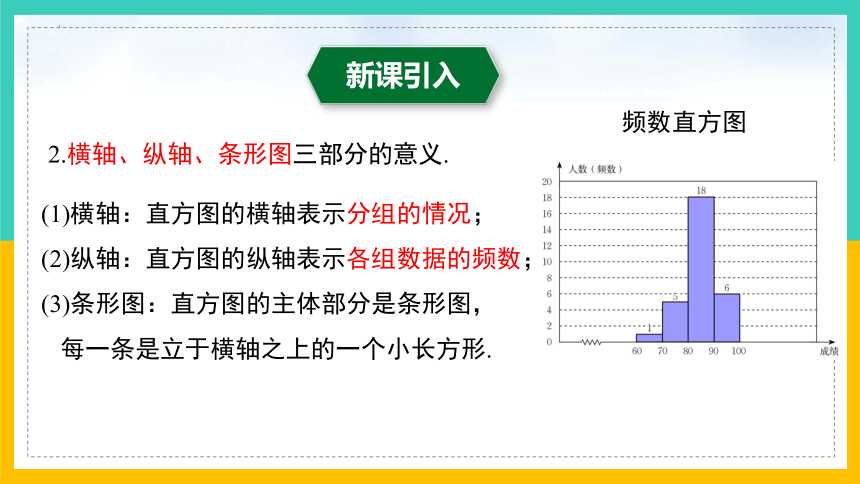
(1)横轴:直方图的横轴表示分组的情况;
(2)纵轴:直方图的纵轴表示各组数据的频数;
(3)条形图:直方图的主体部分是条形图,
每一条是立于横轴之上的一个小长方形.
2.横轴、纵轴、条形图三部分的意义.
核心知识点一
探究学习
制作频数直方图
为了了解某地区新生儿体重状况,某医院随机调取了该地区60名新生儿的出生体重,结果(单位:g)如下:
3850 3900 3300 3500 3315 3800 2550 3800 4150 2 500 2700 2850
3800 3500 2900 2850 3300 3650 4000 3300 2800 2150 3700 3465
3680 2900 3050 3850 3610 3800 3280 3100 3000 2800 3500 4050
3300 3450 3100 3400 4160 3300 2750 3250 2350 3520 3850 2850
3450 3800 3500 3100 1900 3200 3400 3400 3400 3120 3600 2900
将数据适当分组,并绘制相应的频数直方图,图中反映出该地区新生儿体重状况怎样?
解:(1)确定所给数据的最大值和最小值:上述数据中最小值是1900,最大值是4160;
(2)将数据适当分组:最大值和最小值相差4160-1900=2260,考虑以250为组距,2260÷250=9.04,可以考虑分成10组;
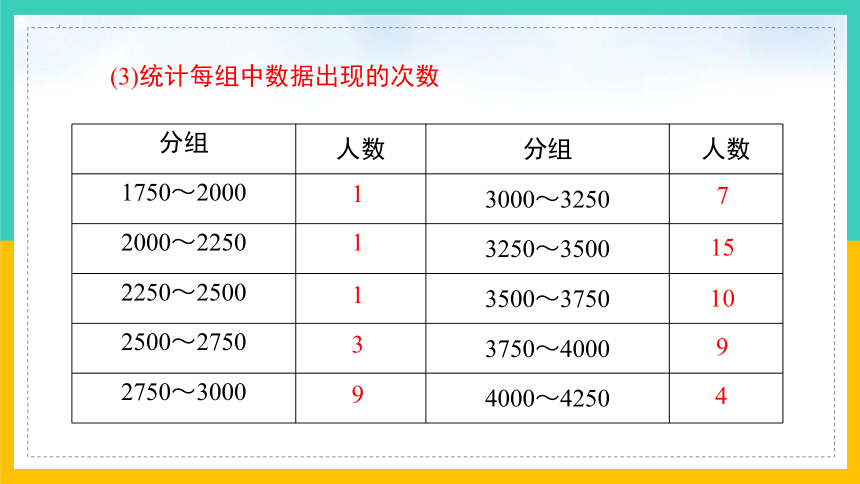
(3)统计每组中数据出现的次数
分组 人数 分组 人数
1750~2000 3000~3250
2000~2250 3250~3500
2250~2500 3500~3750
2500~2750 3750~4000
2750~3000 4000~4250
1
1
1
3
9
7
15
10
9
4
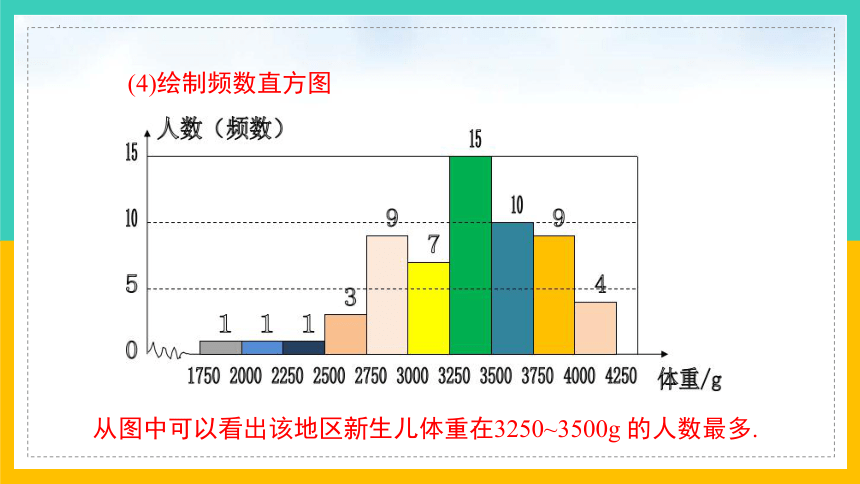
(4)绘制频数直方图
从图中可以看出该地区新生儿体重在3250~3500g 的人数最多.
(1)组距:
每组两个端点之间的距离;各组组距应该相等.
(2)分点:
为了保持组距相等,一般把最小值减去一点作为最左端的分点,把最大值加大一点作为最右端的分点;
另外要使每个数据都落在相应的组内,可以把分点取多一位小数,并把第一组的起点稍减小一点.
频数直方图相关知识
频数直方图相关知识
(3)组数:
分组时如果组数较少,数据过于集中,掩盖了分组特征;
组数较多,数据过于分散,又打乱了分组特征.
组数的多少与样本中所含数据的多少有关,一般情况下,
50个数据以内的,分5~8组;
50到100个数据之间,分8~12组;
100个数据以上,多分为12组为宜.
绘制频数直方图的步骤
(1)计算所给数据的最大值与最小值的差;
(2)确定组距和组数,并将数据适当分组:数据越多,分的组数也应越多,当数据在100个以内时,一般分成5~12组,组距是指每个小组的两个端点之间的距离,一般每个小组的组距相等;确定分点:确定分点的方法不唯一,为了保持相等的组距,往往把一组中的最大的数据增大一点作为右端的分点;
(3)列频数分布表,统计每组中数据出现的次数;
(4)绘制频数直方图.
例:银行在某储蓄所抽样调查了 50 名顾客,他们的等待时间(进入银行到接受受理的时间间隔,单位:min)如下:
将数据适当分组,并绘制相应的频数直方图.
解:(1)确定最大值和最小值:数据中最大值是42,最小值是0.
(2)将数据适当分组:最大值和最小值相差42-0=42,以5为组距,42÷5=8.4,可以考虑分成9组.
(3)统计每组中数据出现的次数.
分组 0~5 5~10 10~15 15~20 20~25 25~30 30~35 35~40 40~45
人数/名 4 2 8 4 11 5 10 2 4
(4)绘制频数直方图.
0
2
4
6
8
10
人数(频数)
等待时间/min
5
10
15
20
25
30
35
40
4
45
12
2
8
4
11
5
10
2
4
随堂练习
1.为了绘制一组数据的频数直方图,首先要算出这组数据的变化范围,数据的变化范围是指数据的( )
A.最大值
B.最小值
C.最大值与最小值的差
D. 个数
C
B
2.如图是某班一次数学测验成绩的频数直方图,则数学成绩在69.5~89.5分范围内的学生占全体学生的( )A.47.5% B.60% C.72.5% D.82.5%
3.如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数直方图,从左起第一、二、三、四四个小长方形的高的比为1∶4∶3∶2,那么该班一分钟跳绳次数是100次以上的学生有( )
A.6人 B.8人
C.16人 D.20人
D
4.一组数据的最小值是12,最大值是38,如果分组的组距相等,且组距为3,则分组后的第一组可以为下列选项中的( )
A.11.5~13.5
B.11.5~14.5
C. 12.5~14.5
D. 12.5~15.5
B
5.如图是20名学生1 min跳绳次数的频数分布直方图,其中跳绳次数为99.5~124.5这一组的频数为( )
A. 5
B. 6
C. 7
D. 8
D
6.如图是某班45名学生每周课外阅读时间的频数分布直方图,由图可知,每周课外阅读时间在6h及以上的人数有( )
A.36人
B.14人
C.8人
D.6人
B
5.某养猪场对200头生猪的质量进行统计,得到频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5 kg及以上的生猪有________头.
140
6.某中学七年级甲、乙两个班参加了一次数学考试,考试人数每班都为40人,每个班的考试成绩分为A,B,C,D,E五个等级.绘制的统计图如图:
根据以上统计图提供的信息,则D等级这一组人数较多的班是________.
甲班
7.某校在“ 数学小论文”评比活动中, 共征集到论文100 篇, 对论文评比的分数(分数为整数) 进行整理后,画出频数直方图( 如图), 已知从左到右5个小长方形的高的比为1 ∶ 3 ∶ 7 ∶ 6 ∶ 3,
那么在这次评比活动中被
评为优秀的论文(分数大于
或等于80 分为优秀)有_____篇.
45
8.在今年“五一”长假期间,某学校团委会要求学生参加一项社会调查活动.八年级学生小青想了解她所居住的小区500户居民的家庭收入情况,从中随机调查了40户居民家庭的收入情况(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图.
根据以上提供的信息,
解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭收入较低(不足1000元)的户数大约有多少户?
分组 频数 频率
600—799 2 0.050
800—999 6 0.150
1000—1199 0.450
1200—1399 9 0.225
1400—1599
1600—1800 2 0.050
合计 40 1.000
解析:(1)在填表时注意计算的顺序,应先计算1400—1599这个小组的频率和频数,再计算小组1000—1199的频数.
(3)数据的中位数应是按从小到大顺序排列后的第20和第21个数的平均数,显然,第20和第21个数都落在1 000—1 199小组内.
(4)用样本估计总体,在500户居民中低收入的占20%.
解:(1)1-0.050-0.150-0.450-0.225-0.050=0.075,40×0.075=3,第五小组的频率和频数分别为0.075和3人;40×0.450=18人,所以第三小组的频数等于18人;
(3)因为收入较低的频率为0.050+0.150=0.2,所以该小区500户居民的家庭收入较低的户数为0.2×500=100(户).
(2)如下图:
课堂小结
①先计算最大值与最小值的差.
②决定组距与组数.
③决定分点
④统计每组中数据出现的次数(频数)
⑤绘制频数分布直方图
制作频数直方图大致步骤:
谢谢聆听
新课标 北师大版
七年级上册
6.3.3数据的表示(第3课时)
第六章
数据的收集与整理
学习目标
1.明确频数直方图制作的步骤,会绘制频数直方图。
2.能从频数分布表和频数直方图中获取有关信息,作出合理的判断和预测。
新课引入
1.定义:频数直方图是一种以频数为纵坐标的条形统计图;
它由横轴、纵轴、条形图三部分组成.
频数直方图
新课引入
频数直方图
(1)横轴:直方图的横轴表示分组的情况;
(2)纵轴:直方图的纵轴表示各组数据的频数;
(3)条形图:直方图的主体部分是条形图,
每一条是立于横轴之上的一个小长方形.
2.横轴、纵轴、条形图三部分的意义.
核心知识点一
探究学习
制作频数直方图
为了了解某地区新生儿体重状况,某医院随机调取了该地区60名新生儿的出生体重,结果(单位:g)如下:
3850 3900 3300 3500 3315 3800 2550 3800 4150 2 500 2700 2850
3800 3500 2900 2850 3300 3650 4000 3300 2800 2150 3700 3465
3680 2900 3050 3850 3610 3800 3280 3100 3000 2800 3500 4050
3300 3450 3100 3400 4160 3300 2750 3250 2350 3520 3850 2850
3450 3800 3500 3100 1900 3200 3400 3400 3400 3120 3600 2900
将数据适当分组,并绘制相应的频数直方图,图中反映出该地区新生儿体重状况怎样?
解:(1)确定所给数据的最大值和最小值:上述数据中最小值是1900,最大值是4160;
(2)将数据适当分组:最大值和最小值相差4160-1900=2260,考虑以250为组距,2260÷250=9.04,可以考虑分成10组;
(3)统计每组中数据出现的次数
分组 人数 分组 人数
1750~2000 3000~3250
2000~2250 3250~3500
2250~2500 3500~3750
2500~2750 3750~4000
2750~3000 4000~4250
1
1
1
3
9
7
15
10
9
4
(4)绘制频数直方图
从图中可以看出该地区新生儿体重在3250~3500g 的人数最多.
(1)组距:
每组两个端点之间的距离;各组组距应该相等.
(2)分点:
为了保持组距相等,一般把最小值减去一点作为最左端的分点,把最大值加大一点作为最右端的分点;
另外要使每个数据都落在相应的组内,可以把分点取多一位小数,并把第一组的起点稍减小一点.
频数直方图相关知识
频数直方图相关知识
(3)组数:
分组时如果组数较少,数据过于集中,掩盖了分组特征;
组数较多,数据过于分散,又打乱了分组特征.
组数的多少与样本中所含数据的多少有关,一般情况下,
50个数据以内的,分5~8组;
50到100个数据之间,分8~12组;
100个数据以上,多分为12组为宜.
绘制频数直方图的步骤
(1)计算所给数据的最大值与最小值的差;
(2)确定组距和组数,并将数据适当分组:数据越多,分的组数也应越多,当数据在100个以内时,一般分成5~12组,组距是指每个小组的两个端点之间的距离,一般每个小组的组距相等;确定分点:确定分点的方法不唯一,为了保持相等的组距,往往把一组中的最大的数据增大一点作为右端的分点;
(3)列频数分布表,统计每组中数据出现的次数;
(4)绘制频数直方图.
例:银行在某储蓄所抽样调查了 50 名顾客,他们的等待时间(进入银行到接受受理的时间间隔,单位:min)如下:
将数据适当分组,并绘制相应的频数直方图.
解:(1)确定最大值和最小值:数据中最大值是42,最小值是0.
(2)将数据适当分组:最大值和最小值相差42-0=42,以5为组距,42÷5=8.4,可以考虑分成9组.
(3)统计每组中数据出现的次数.
分组 0~5 5~10 10~15 15~20 20~25 25~30 30~35 35~40 40~45
人数/名 4 2 8 4 11 5 10 2 4
(4)绘制频数直方图.
0
2
4
6
8
10
人数(频数)
等待时间/min
5
10
15
20
25
30
35
40
4
45
12
2
8
4
11
5
10
2
4
随堂练习
1.为了绘制一组数据的频数直方图,首先要算出这组数据的变化范围,数据的变化范围是指数据的( )
A.最大值
B.最小值
C.最大值与最小值的差
D. 个数
C
B
2.如图是某班一次数学测验成绩的频数直方图,则数学成绩在69.5~89.5分范围内的学生占全体学生的( )A.47.5% B.60% C.72.5% D.82.5%
3.如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数直方图,从左起第一、二、三、四四个小长方形的高的比为1∶4∶3∶2,那么该班一分钟跳绳次数是100次以上的学生有( )
A.6人 B.8人
C.16人 D.20人
D
4.一组数据的最小值是12,最大值是38,如果分组的组距相等,且组距为3,则分组后的第一组可以为下列选项中的( )
A.11.5~13.5
B.11.5~14.5
C. 12.5~14.5
D. 12.5~15.5
B
5.如图是20名学生1 min跳绳次数的频数分布直方图,其中跳绳次数为99.5~124.5这一组的频数为( )
A. 5
B. 6
C. 7
D. 8
D
6.如图是某班45名学生每周课外阅读时间的频数分布直方图,由图可知,每周课外阅读时间在6h及以上的人数有( )
A.36人
B.14人
C.8人
D.6人
B
5.某养猪场对200头生猪的质量进行统计,得到频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5 kg及以上的生猪有________头.
140
6.某中学七年级甲、乙两个班参加了一次数学考试,考试人数每班都为40人,每个班的考试成绩分为A,B,C,D,E五个等级.绘制的统计图如图:
根据以上统计图提供的信息,则D等级这一组人数较多的班是________.
甲班
7.某校在“ 数学小论文”评比活动中, 共征集到论文100 篇, 对论文评比的分数(分数为整数) 进行整理后,画出频数直方图( 如图), 已知从左到右5个小长方形的高的比为1 ∶ 3 ∶ 7 ∶ 6 ∶ 3,
那么在这次评比活动中被
评为优秀的论文(分数大于
或等于80 分为优秀)有_____篇.
45
8.在今年“五一”长假期间,某学校团委会要求学生参加一项社会调查活动.八年级学生小青想了解她所居住的小区500户居民的家庭收入情况,从中随机调查了40户居民家庭的收入情况(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图.
根据以上提供的信息,
解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭收入较低(不足1000元)的户数大约有多少户?
分组 频数 频率
600—799 2 0.050
800—999 6 0.150
1000—1199 0.450
1200—1399 9 0.225
1400—1599
1600—1800 2 0.050
合计 40 1.000
解析:(1)在填表时注意计算的顺序,应先计算1400—1599这个小组的频率和频数,再计算小组1000—1199的频数.
(3)数据的中位数应是按从小到大顺序排列后的第20和第21个数的平均数,显然,第20和第21个数都落在1 000—1 199小组内.
(4)用样本估计总体,在500户居民中低收入的占20%.
解:(1)1-0.050-0.150-0.450-0.225-0.050=0.075,40×0.075=3,第五小组的频率和频数分别为0.075和3人;40×0.450=18人,所以第三小组的频数等于18人;
(3)因为收入较低的频率为0.050+0.150=0.2,所以该小区500户居民的家庭收入较低的户数为0.2×500=100(户).
(2)如下图:
课堂小结
①先计算最大值与最小值的差.
②决定组距与组数.
③决定分点
④统计每组中数据出现的次数(频数)
⑤绘制频数分布直方图
制作频数直方图大致步骤:
谢谢聆听
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
