5.2.4 二次函数的图像和性质-第4课时 课件(26张ppt)-2023-2024学年九年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 5.2.4 二次函数的图像和性质-第4课时 课件(26张ppt)-2023-2024学年九年级数学下册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 33.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 00:00:00 | ||
图片预览







文档简介
5.2.4 二次函数的图像和性质-第4课时
第5章 二次函数
教学目标
01
能用配方法把二次函数的一般式y=ax2+bx+c(a≠0)转化成顶点式y=a(x-h)2+k(a≠0)
02
能根据二次函数的一般式描述函数的开口方向、对称轴、顶点坐标、增减性、最值等
二次函数y=ax2+bx+c
(a≠0)的图像和性质
Q1-1:如何平移y=ax2(a≠0)的图像得到y=a(x-h)2+k(a≠0)的图像?
Q1-2:请描述y=a(x-h)2+k(a≠0)的图像和性质。
当a>0时,图像开口向上,顶点坐标为:(h,k),对称轴为:x=h,图像先减后增,当x=h时,函数有最小值k;
01
复习引入
向右平移h个单位,向上平移k个单位
当a<0时,图像开口向下,顶点坐标为:(h,k),对称轴为:x=h,图像先增后减,当x=h时,函数有最大值k。
∵y=2x2向右平移2个单位,向上平移1个单位,即可得到y=(x-2)2+1;
∴y=2x2向右平移2个单位,向上平移1个单位,即可得到y=x2-4x+5。
【举例】y=x2-4x+5
01
情境引入
Q2:y=ax2+bx+c(a≠0)的图像能否由y=ax2(a≠0)的图像平移得到?
配方得:y=x2-4x+4+1=(x-2)2+1
【猜想】y=ax2+bx+c(a≠0)的图像可以由y=ax2(a≠0)的图像平移得到
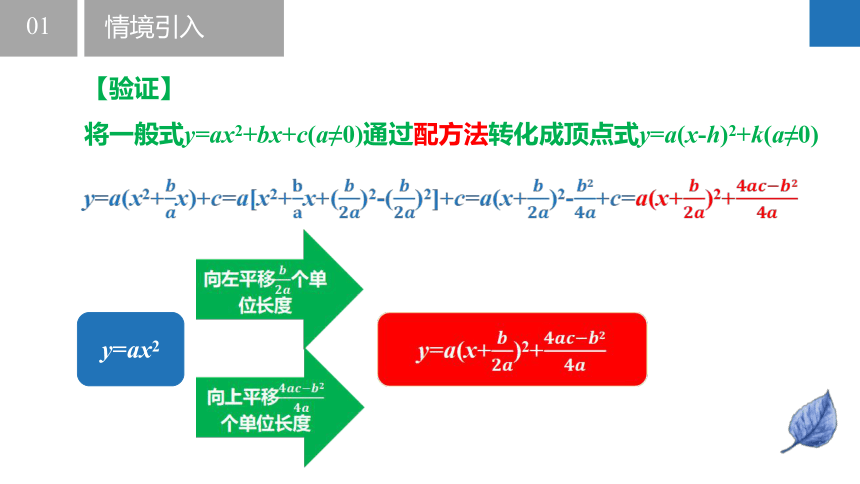
【验证】
将一般式y=ax2+bx+c(a≠0)通过配方法转化成顶点式y=a(x-h)2+k(a≠0)
y=a(x2+????????x)+c=a[x2+????????x+(????????????)2-(????????????)2]+c=a(x+????????????)2-????????????????+c=a(x+????????????)2+?????????????????????????????
?
01
情境引入
y=ax2
向左平移????????????个单位长度
?
向上平移?????????????????????????????个单位长度
?
y=a(x+????????????)2+?????????????????????????????
?
02
知识精讲
一般式转化为顶点式
一般式转化为顶点式:y=ax2+bx+c=a(x+????????????)2+?????????????????????????????(a≠0)
?
y=ax2+bx+c(a≠0)的图像是由y=ax2(a≠0)的图像向左平移????????????个单位长度,向上平移?????????????????????????????个单位长度得到
?
练一练1:将y=????????x2-6x+21转化为顶点式。
?
【分析】y=????????(x2-12x)+21
=????????(x2-12x+36-36)+21
=????????(x-6)2-18+21
=????????(x-6)2+3
?
02
知识精讲
练一练2:y=????????x2-6x+21的图像是由y=????????x2的图像怎样变换得到?
?
02
知识精讲
【分析】y=????????x2-6x+21=????????(x-6)2+3的图像是由y=????????x2的图像向右平移6个单位长度,向上平移3个单位长度得到
?
练一练3:请描述y=????????x2-6x+21的图像和性质。
?
02
知识精讲
【分析】y=????????x2-6x+21=????????(x-6)2+3,
图像开口向上,
顶点坐标为:(6,3),
对称轴为:x=6,
当x<6时,y随x增大而减小,当x>6时,y随x增大而增大,
当x=6时,函数有最小值3。
?
a的正负
图像
开口
顶点坐标
对称轴
增减性
a>0
向上
(-,)
直线x=-
当x<-时,y随x增大而减小
当x>-时,y随x增大而增大
当x=-时,y取最小值
a<0
向下
(-,)
直线x=-
当x<-时,y随x增大而增大
当x>-时,y随x增大而减小
当x=-时,y取最大值
知识精讲
y=ax2+bx+c(a≠0)的图像和性质
02
知识精讲
一般式y=ax2+bx+c(a≠0)→顶点式y=a(x+????????????)2+?????????????????????????????(a≠0)
?
例1、用配方法把下列函数写成y=a(x-h)2+k的形式,并画出函数图像,写出它们的开口方向、对称轴、顶点坐标、增减性、最值。
(1)y=x2+6x+1;
(2)y=2x2+8x-8;
(3)y=-3x2-6x+1。
03
典例精析
(1)y=x2+6x+1;
解:(1)y=(x2+6x+9-9)+1
=(x+3)2-9+1
=(x+3)2-8;
图像开口向上,
顶点坐标为:(-3,-8),
对称轴为:x=-3,
当x<-3时,y随x增大而减小,当x>-3时,y随x增大而增大,
当x=-3时,函数有最小值-8。
03
典例精析
(2)y=2x2+8x-8;
(2)y=2(x2+4x+4-4)-8
=2(x+2)2-8-8
=2(x+2)2-16;
图像开口向上,
顶点坐标为:(-2,-16),
对称轴为:x=-2,
当x<-2时,y随x增大而减小,当x>-2时,y随x增大而增大,
当x=-2时,函数有最小值-16。
03
典例精析
(3)y=-3x2-6x+1。
(3)y=-3(x2+2x+1-1)+1
=-3(x+1)2+3+1
=-3(x+1)2+4;
图像开口向下,
顶点坐标为:(-1,4),
对称轴为:x=-1,
当x<-1时,y随x增大而增大,当x>-1时,y随x增大而减小,
当x=-1时,函数有最大值4。
03
典例精析
例2、(1)抛物线y=x2-2x+3对称轴为( )
A. 直线x=-1 B. 直线x=-2
C. 直线x=1 D. 直线x=2
【法一:配方法】
∵y=x2-2x+3=(x-1)2+2,
∴对称轴为直线x=1。
C
对称轴
直线x=-
03
典例精析
【法二:公式法】
∵a=1,b=-2,
∴对称轴为直线x=-????????????=1。
?
公式法更简单
例2、(2)若二次函数y=2x2-ax-a+1的图像的对称轴是y轴,则a的值是( )
A. 0 B. 1 C. -1 D. 2
【公式法】
∵a=2,b=-a,
∴对称轴为直线x=-????????????=????????=0。
?
A
03
典例精析
例3、(1)二次函数y=2x2-x,当x_____时,y随x增大而增大,当x_____时,y随x增大而减小。
【分析】∵a=2>0,b=-1,
∴x对=-????????????=????????。
?
>????????
?
?
03
典例精析
a的正负
对称轴
增减性
a>0
直线x=-
当x<-时,y随x增大而减小
当x>-时,y随x增大而增大
当x=-时,y取最小值
例3、(2)已知二次函数y=-x2+bx+c,当2b≤4
03
典例精析
a的正负
对称轴
增减性
a<0
直线x=-
当x<-时,y随x增大而增大
当x>-时,y随x增大而减小
当x=-时,y取最大值
【分析】
∵a=-1<0,
∴x对=-??????????=????????,
∴当x>????????时,y随x增大而减小,
∵当2?
例4、(1)若二次函数y=x2-6x+c的图像过A(-1,y1),B(2,y2),C(3+????,y3),则y1、y2、y3的大小关系是( )
A. y1>y2>y3 B. y1>y3>y2
C. y2>y1>y3 D. y3>y1>y2
?
【分析】
将x1=-1,x2=2,x3=3分别代入,
可得:y1=7+c,y2=-8+c,y3=-7+c,
即y1>y3>y2。
B
03
典例精析
例4、(2)若A(-????????????,y1),B(-????????,y2),C(????????,y3)为二次函数y=-x2+4x-5的图像上的三点,则y1、y2、y3的大小关系是( )
A. y1B. y2C. y3D. y1?
A
法二:利用增减性
∵a=-1<0,-????????????=2,
当x<2时,y随x的增大而增大,
?
∵-????????????<-????????∴y1?
03
典例精析
【分析】法一:
同上题——直接代入x值,求出y值,再比较大小
例5、(1)抛物线y=(k-1)x2+(2-2k)x+1,那么此抛物线的对称轴是直线_____,它必定经过点_____和_____。
【分析】
x=-????????????=-2
?
∵过定点,
∴y的值与k无关,
∴含有k的项合并同类项后,系数为0。
x=-2
∵y=(k-1)x2+(2-2k)x+1
=(x2-2x)k+(-x2+2x+1),
∴x2-2x=0,解得:x=0或x=2,
∴定点为(0,1)和(2,1)。
(0,1)
(2,1)
03
典例精析
例5、(2)二次函数y=ax2+2ak+ak2+k,当k取不同值时,图像顶点所在的直线是( )
A. y=x
B. x轴
C. y=-x
D. y轴
【分析】
1、当k取不同值时,顶点在变
2、两点确定一条直线
【解题策略】赋值法:令k=0,k=-1
1、先分别这两种情况下求出二次函数的顶点
2、再用待定系数法求过这两点的直线
03
典例精析
03
典例精析
例5、(2)二次函数y=ax2+2ak+ak2+k,当k取不同值时,图像顶点所在的直线是( )
A. y=x
B. x轴
C. y=-x
D. y轴
C
设过A、B两点的直线解析式为y=kx+b,
则????=?????????+????=????,解得:????=????????=?????,即y=-x。
?
令k=0,原函数可化为y=ax2,
此时顶点坐标为A(0,0);
令k=1,原函数可化为y=a(x+1)2+1,
此时顶点坐标为B(-1,1);
课后总结
一般式转化为顶点式:y=ax2+bx+c=a(x+????????????)2+?????????????????????????????(a≠0)
?
y=ax2+bx+c(a≠0)的图像是由y=ax2(a≠0)的图像向左平移????????????个单位长度,向上平移?????????????????????????????个单位长度得到
?
课后总结
a的正负
图像
开口
顶点坐标
对称轴
增减性
a>0
向上
(-,)
直线x=-
当x<-时,y随x增大而减小
当x>-时,y随x增大而增大
当x=-时,y取最小值
a<0
向下
(-,)
直线x=-
当x<-时,y随x增大而增大
当x>-时,y随x增大而减小
当x=-时,y取最大值
一般式y=ax2+bx+c(a≠0)→顶点式y=a(x+????????????)2+?????????????????????????????(a≠0)
第5章 二次函数
教学目标
01
能用配方法把二次函数的一般式y=ax2+bx+c(a≠0)转化成顶点式y=a(x-h)2+k(a≠0)
02
能根据二次函数的一般式描述函数的开口方向、对称轴、顶点坐标、增减性、最值等
二次函数y=ax2+bx+c
(a≠0)的图像和性质
Q1-1:如何平移y=ax2(a≠0)的图像得到y=a(x-h)2+k(a≠0)的图像?
Q1-2:请描述y=a(x-h)2+k(a≠0)的图像和性质。
当a>0时,图像开口向上,顶点坐标为:(h,k),对称轴为:x=h,图像先减后增,当x=h时,函数有最小值k;
01
复习引入
向右平移h个单位,向上平移k个单位
当a<0时,图像开口向下,顶点坐标为:(h,k),对称轴为:x=h,图像先增后减,当x=h时,函数有最大值k。
∵y=2x2向右平移2个单位,向上平移1个单位,即可得到y=(x-2)2+1;
∴y=2x2向右平移2个单位,向上平移1个单位,即可得到y=x2-4x+5。
【举例】y=x2-4x+5
01
情境引入
Q2:y=ax2+bx+c(a≠0)的图像能否由y=ax2(a≠0)的图像平移得到?
配方得:y=x2-4x+4+1=(x-2)2+1
【猜想】y=ax2+bx+c(a≠0)的图像可以由y=ax2(a≠0)的图像平移得到
【验证】
将一般式y=ax2+bx+c(a≠0)通过配方法转化成顶点式y=a(x-h)2+k(a≠0)
y=a(x2+????????x)+c=a[x2+????????x+(????????????)2-(????????????)2]+c=a(x+????????????)2-????????????????+c=a(x+????????????)2+?????????????????????????????
?
01
情境引入
y=ax2
向左平移????????????个单位长度
?
向上平移?????????????????????????????个单位长度
?
y=a(x+????????????)2+?????????????????????????????
?
02
知识精讲
一般式转化为顶点式
一般式转化为顶点式:y=ax2+bx+c=a(x+????????????)2+?????????????????????????????(a≠0)
?
y=ax2+bx+c(a≠0)的图像是由y=ax2(a≠0)的图像向左平移????????????个单位长度,向上平移?????????????????????????????个单位长度得到
?
练一练1:将y=????????x2-6x+21转化为顶点式。
?
【分析】y=????????(x2-12x)+21
=????????(x2-12x+36-36)+21
=????????(x-6)2-18+21
=????????(x-6)2+3
?
02
知识精讲
练一练2:y=????????x2-6x+21的图像是由y=????????x2的图像怎样变换得到?
?
02
知识精讲
【分析】y=????????x2-6x+21=????????(x-6)2+3的图像是由y=????????x2的图像向右平移6个单位长度,向上平移3个单位长度得到
?
练一练3:请描述y=????????x2-6x+21的图像和性质。
?
02
知识精讲
【分析】y=????????x2-6x+21=????????(x-6)2+3,
图像开口向上,
顶点坐标为:(6,3),
对称轴为:x=6,
当x<6时,y随x增大而减小,当x>6时,y随x增大而增大,
当x=6时,函数有最小值3。
?
a的正负
图像
开口
顶点坐标
对称轴
增减性
a>0
向上
(-,)
直线x=-
当x<-时,y随x增大而减小
当x>-时,y随x增大而增大
当x=-时,y取最小值
a<0
向下
(-,)
直线x=-
当x<-时,y随x增大而增大
当x>-时,y随x增大而减小
当x=-时,y取最大值
知识精讲
y=ax2+bx+c(a≠0)的图像和性质
02
知识精讲
一般式y=ax2+bx+c(a≠0)→顶点式y=a(x+????????????)2+?????????????????????????????(a≠0)
?
例1、用配方法把下列函数写成y=a(x-h)2+k的形式,并画出函数图像,写出它们的开口方向、对称轴、顶点坐标、增减性、最值。
(1)y=x2+6x+1;
(2)y=2x2+8x-8;
(3)y=-3x2-6x+1。
03
典例精析
(1)y=x2+6x+1;
解:(1)y=(x2+6x+9-9)+1
=(x+3)2-9+1
=(x+3)2-8;
图像开口向上,
顶点坐标为:(-3,-8),
对称轴为:x=-3,
当x<-3时,y随x增大而减小,当x>-3时,y随x增大而增大,
当x=-3时,函数有最小值-8。
03
典例精析
(2)y=2x2+8x-8;
(2)y=2(x2+4x+4-4)-8
=2(x+2)2-8-8
=2(x+2)2-16;
图像开口向上,
顶点坐标为:(-2,-16),
对称轴为:x=-2,
当x<-2时,y随x增大而减小,当x>-2时,y随x增大而增大,
当x=-2时,函数有最小值-16。
03
典例精析
(3)y=-3x2-6x+1。
(3)y=-3(x2+2x+1-1)+1
=-3(x+1)2+3+1
=-3(x+1)2+4;
图像开口向下,
顶点坐标为:(-1,4),
对称轴为:x=-1,
当x<-1时,y随x增大而增大,当x>-1时,y随x增大而减小,
当x=-1时,函数有最大值4。
03
典例精析
例2、(1)抛物线y=x2-2x+3对称轴为( )
A. 直线x=-1 B. 直线x=-2
C. 直线x=1 D. 直线x=2
【法一:配方法】
∵y=x2-2x+3=(x-1)2+2,
∴对称轴为直线x=1。
C
对称轴
直线x=-
03
典例精析
【法二:公式法】
∵a=1,b=-2,
∴对称轴为直线x=-????????????=1。
?
公式法更简单
例2、(2)若二次函数y=2x2-ax-a+1的图像的对称轴是y轴,则a的值是( )
A. 0 B. 1 C. -1 D. 2
【公式法】
∵a=2,b=-a,
∴对称轴为直线x=-????????????=????????=0。
?
A
03
典例精析
例3、(1)二次函数y=2x2-x,当x_____时,y随x增大而增大,当x_____时,y随x增大而减小。
【分析】∵a=2>0,b=-1,
∴x对=-????????????=????????。
?
>????????
?
?
03
典例精析
a的正负
对称轴
增减性
a>0
直线x=-
当x<-时,y随x增大而减小
当x>-时,y随x增大而增大
当x=-时,y取最小值
例3、(2)已知二次函数y=-x2+bx+c,当2
03
典例精析
a的正负
对称轴
增减性
a<0
直线x=-
当x<-时,y随x增大而增大
当x>-时,y随x增大而减小
当x=-时,y取最大值
【分析】
∵a=-1<0,
∴x对=-??????????=????????,
∴当x>????????时,y随x增大而减小,
∵当2
例4、(1)若二次函数y=x2-6x+c的图像过A(-1,y1),B(2,y2),C(3+????,y3),则y1、y2、y3的大小关系是( )
A. y1>y2>y3 B. y1>y3>y2
C. y2>y1>y3 D. y3>y1>y2
?
【分析】
将x1=-1,x2=2,x3=3分别代入,
可得:y1=7+c,y2=-8+c,y3=-7+c,
即y1>y3>y2。
B
03
典例精析
例4、(2)若A(-????????????,y1),B(-????????,y2),C(????????,y3)为二次函数y=-x2+4x-5的图像上的三点,则y1、y2、y3的大小关系是( )
A. y1
A
法二:利用增减性
∵a=-1<0,-????????????=2,
当x<2时,y随x的增大而增大,
?
∵-????????????<-????????∴y1
03
典例精析
【分析】法一:
同上题——直接代入x值,求出y值,再比较大小
例5、(1)抛物线y=(k-1)x2+(2-2k)x+1,那么此抛物线的对称轴是直线_____,它必定经过点_____和_____。
【分析】
x=-????????????=-2
?
∵过定点,
∴y的值与k无关,
∴含有k的项合并同类项后,系数为0。
x=-2
∵y=(k-1)x2+(2-2k)x+1
=(x2-2x)k+(-x2+2x+1),
∴x2-2x=0,解得:x=0或x=2,
∴定点为(0,1)和(2,1)。
(0,1)
(2,1)
03
典例精析
例5、(2)二次函数y=ax2+2ak+ak2+k,当k取不同值时,图像顶点所在的直线是( )
A. y=x
B. x轴
C. y=-x
D. y轴
【分析】
1、当k取不同值时,顶点在变
2、两点确定一条直线
【解题策略】赋值法:令k=0,k=-1
1、先分别这两种情况下求出二次函数的顶点
2、再用待定系数法求过这两点的直线
03
典例精析
03
典例精析
例5、(2)二次函数y=ax2+2ak+ak2+k,当k取不同值时,图像顶点所在的直线是( )
A. y=x
B. x轴
C. y=-x
D. y轴
C
设过A、B两点的直线解析式为y=kx+b,
则????=?????????+????=????,解得:????=????????=?????,即y=-x。
?
令k=0,原函数可化为y=ax2,
此时顶点坐标为A(0,0);
令k=1,原函数可化为y=a(x+1)2+1,
此时顶点坐标为B(-1,1);
课后总结
一般式转化为顶点式:y=ax2+bx+c=a(x+????????????)2+?????????????????????????????(a≠0)
?
y=ax2+bx+c(a≠0)的图像是由y=ax2(a≠0)的图像向左平移????????????个单位长度,向上平移?????????????????????????????个单位长度得到
?
课后总结
a的正负
图像
开口
顶点坐标
对称轴
增减性
a>0
向上
(-,)
直线x=-
当x<-时,y随x增大而减小
当x>-时,y随x增大而增大
当x=-时,y取最小值
a<0
向下
(-,)
直线x=-
当x<-时,y随x增大而增大
当x>-时,y随x增大而减小
当x=-时,y取最大值
一般式y=ax2+bx+c(a≠0)→顶点式y=a(x+????????????)2+?????????????????????????????(a≠0)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
