等腰三角形在圆中的应用 教案
文档属性
| 名称 | 等腰三角形在圆中的应用 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 61.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-17 14:00:15 | ||
图片预览

文档简介
等腰三角形在圆中应用
复习目标
复习等腰三角形的“三线合一”性质在圆的证明与计算中的运用。
2.圆与等腰三角形有关的基本图形及相关计算。
3垂径定理与勾股定理
4.利用三角函数或相似解决问题。
二,教案
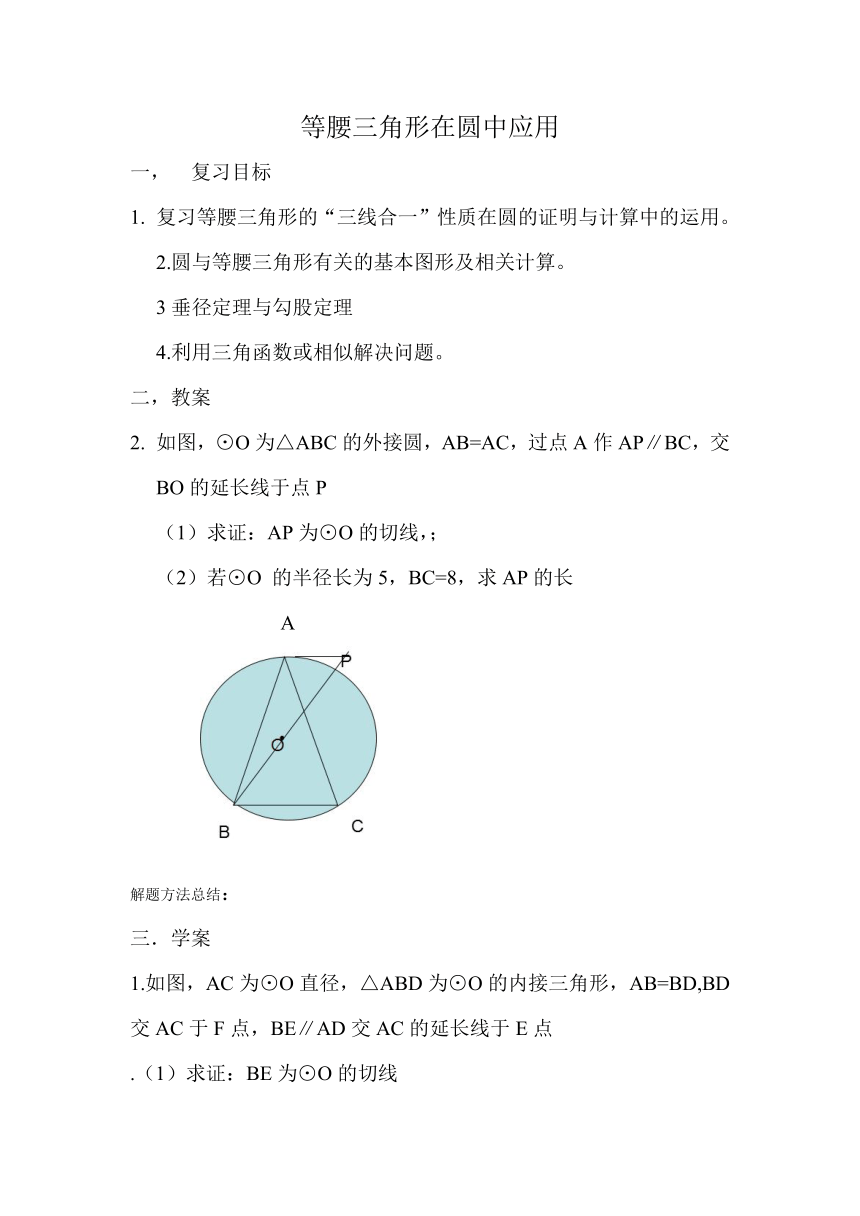
如图,⊙O为△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P
(1)求证:AP为⊙O的切线,;
(2)若⊙O 的半径长为5,BC=8,求AP的长
A
解题方法总结:
三.学案
1.如图,AC为⊙O直径,△ABD为⊙O的内接三角形,AB=BD,BD交AC于F点,BE∥AD交AC的延长线于E点
.(1)求证:BE为⊙O的切线
(2)若AF=4CF,求tan∠E的值。
2.如图,在△ABD中,∠ADB=45°,⊙O经过A、B、D三点,BE=BD,过点A作AM⊥ED于M.
(1)求证:AM为⊙O的切线
(2)若∠ABD=22.5°,DM=1,求⊙O 的半径
四,练案
1.如图,⊙O为△ABC的外接圆,AB=BC,D为⊙O上一点,DB=DC,DB交AC于F.
(1)求证:BC=CF
(2)若cos∠BAC= 求DA/DB的值。
五,知识点及数学思想总结
一,知识点总结:
连接等腰三角形的顶点与圆心交底边于某一点的线段构成等腰三角形的三线。
1.它为证明切线提供了的90°的角。
2.它为与顶角相等的圆周角提供了相等的角并放在直角三角形中,为三角函数提供了平台。
3.它为构造特殊的平行四边形如矩形,正方形,及X形的平行等基本图形提供支持。
二,本课数学思想总结:
1.代数思想
2.数形结合
3.转化思想
复习目标
复习等腰三角形的“三线合一”性质在圆的证明与计算中的运用。
2.圆与等腰三角形有关的基本图形及相关计算。
3垂径定理与勾股定理
4.利用三角函数或相似解决问题。
二,教案
如图,⊙O为△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P
(1)求证:AP为⊙O的切线,;
(2)若⊙O 的半径长为5,BC=8,求AP的长
A
解题方法总结:
三.学案
1.如图,AC为⊙O直径,△ABD为⊙O的内接三角形,AB=BD,BD交AC于F点,BE∥AD交AC的延长线于E点
.(1)求证:BE为⊙O的切线
(2)若AF=4CF,求tan∠E的值。
2.如图,在△ABD中,∠ADB=45°,⊙O经过A、B、D三点,BE=BD,过点A作AM⊥ED于M.
(1)求证:AM为⊙O的切线
(2)若∠ABD=22.5°,DM=1,求⊙O 的半径
四,练案
1.如图,⊙O为△ABC的外接圆,AB=BC,D为⊙O上一点,DB=DC,DB交AC于F.
(1)求证:BC=CF
(2)若cos∠BAC= 求DA/DB的值。
五,知识点及数学思想总结
一,知识点总结:
连接等腰三角形的顶点与圆心交底边于某一点的线段构成等腰三角形的三线。
1.它为证明切线提供了的90°的角。
2.它为与顶角相等的圆周角提供了相等的角并放在直角三角形中,为三角函数提供了平台。
3.它为构造特殊的平行四边形如矩形,正方形,及X形的平行等基本图形提供支持。
二,本课数学思想总结:
1.代数思想
2.数形结合
3.转化思想
同课章节目录
