24.4解直角三角形分层练习(含答案)
文档属性
| 名称 | 24.4解直角三角形分层练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 887.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
24.4解直角三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某铁路路基的横断面是一个等腰梯形(如图),若腰的坡比为2:3,路基顶宽3米,高4米,则路基的下底宽为( )
A.7米 B.9米 C.12米 D.15米
2.如图,已知第一象限的点A在反比例函数y=上,过点A作AB⊥AO交x轴于点B,∠AOB=30°,将△AOB绕点O逆时针旋转120°,点B的对应点B恰好落在反比例函数y=上,则k的值为( )
A.﹣4 B.﹣ C.﹣2 D.﹣
3.在△ABC中,∠C=90°,∠BAC=30°,AD是中线,则tan∠CDA的值为( )
A.3 B.2 C. D.
4.在△ABC中,∠C=90°,sinB=,b=,则a等于( )
A. B.1 C.2 D.3
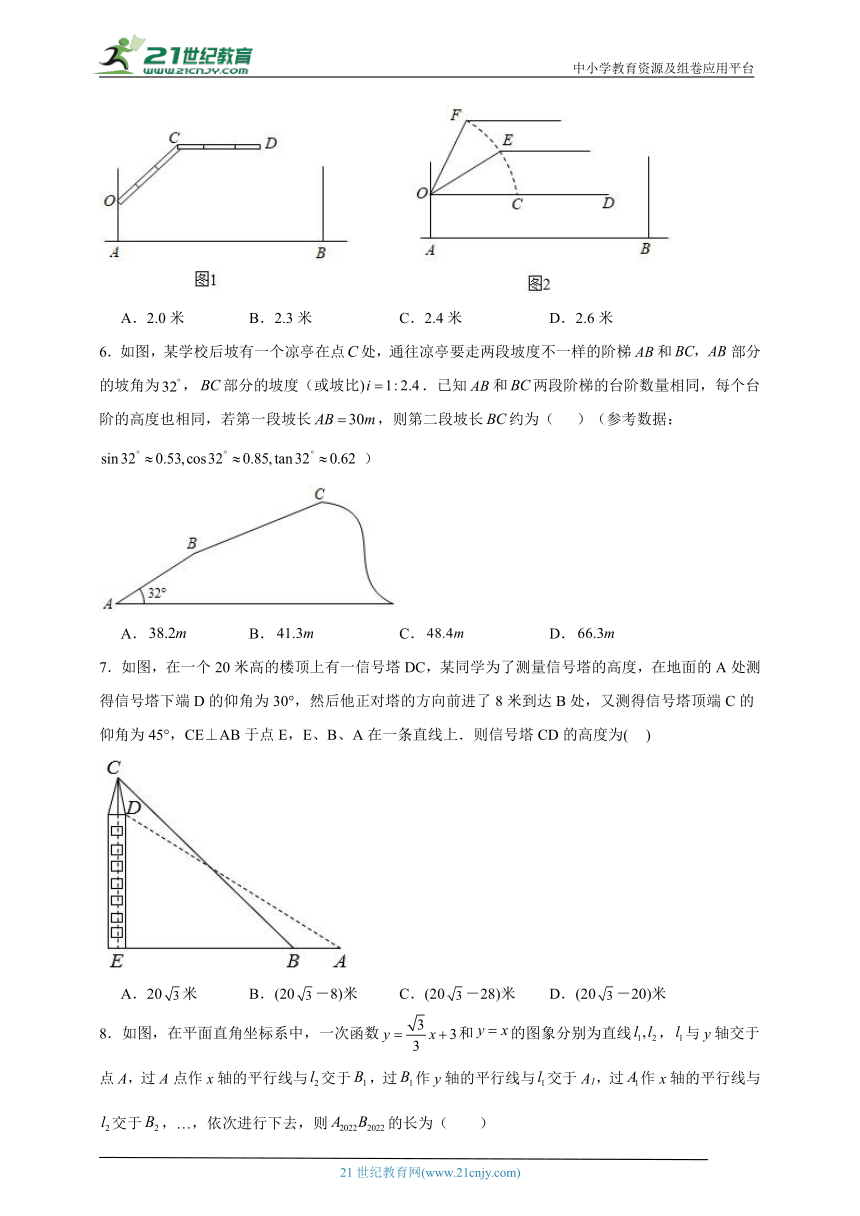
5.如图1,某小区入口处安装“曲臂杆”,OA⊥AB,OA=1米,点O是臂杆转动的支点,点C是曲臂杆两段的连接点,曲臂杆CD部分始终与AB平行.如图2,曲臂杆初始位置时O、C、D三点共线,当曲臂杆升高到OE时,∠AOE=121°,点E到AB的距离是1.7米,当曲臂杆升高到OF时,∠AOF=156°,则点F到AB的距离是(结果精确到0.1米,参考数据:sin31°≈0.5,sin66°≈0.9)( )
A.2.0米 B.2.3米 C.2.4米 D.2.6米
6.如图,某学校后坡有一个凉亭在点处,通往凉亭要走两段坡度不一样的阶梯和部分的坡角为,部分的坡度(或坡比).已知和两段阶梯的台阶数量相同,每个台阶的高度也相同,若第一段坡长,则第二段坡长约为( )(参考数据: )
A. B. C. D.
7.如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达B处,又测得信号塔顶端C的仰角为45°,CE⊥AB于点E,E、B、A在一条直线上.则信号塔CD的高度为( )
A.20米 B.(20-8)米 C.(20-28)米 D.(20-20)米
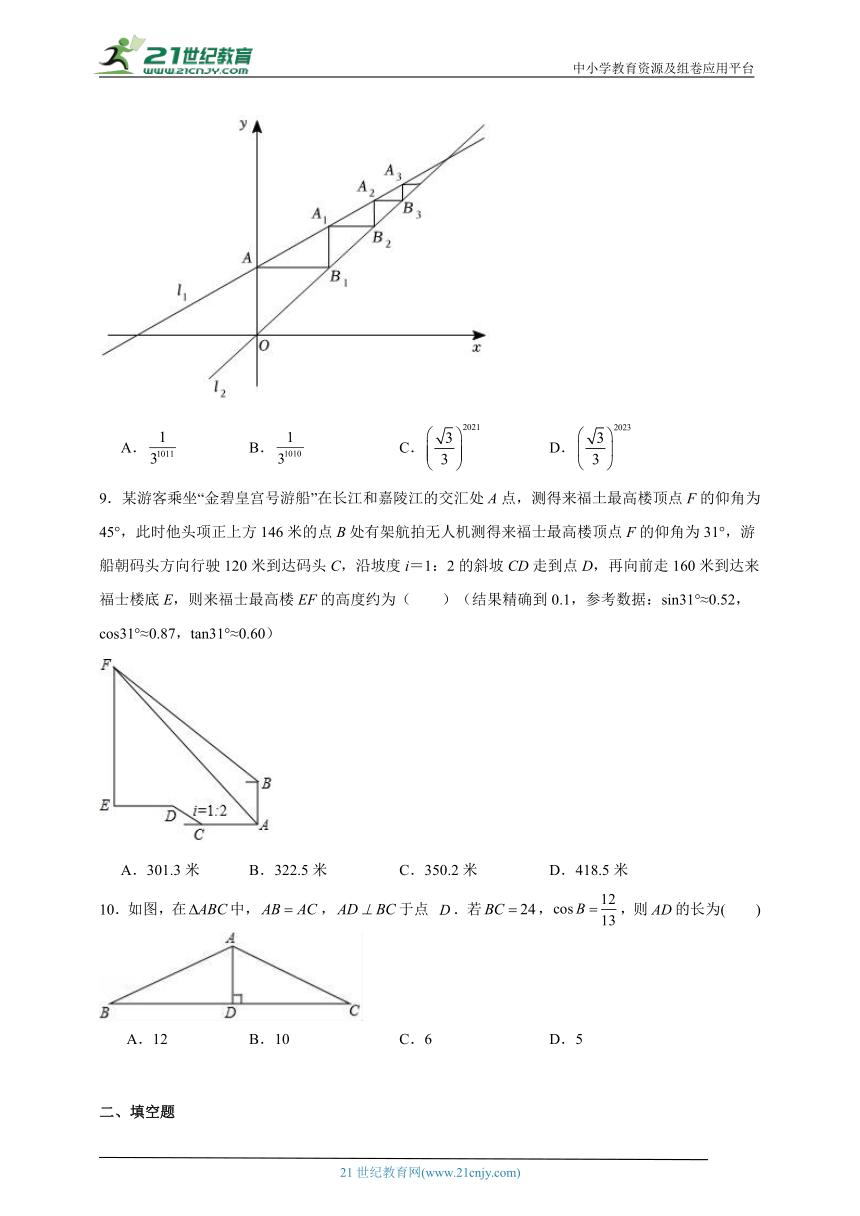
8.如图,在平面直角坐标系中,一次函数和的图象分别为直线,与y轴交于点A,过A点作x轴的平行线与交于,过作y轴的平行线与交于A1,过作x轴的平行线与交于,…,依次进行下去,则的长为( )
A. B. C. D.
9.某游客乘坐“金碧皇宫号游船”在长江和嘉陵江的交汇处A点,测得来福土最高楼顶点F的仰角为45°,此时他头项正上方146米的点B处有架航拍无人机测得来福士最高楼顶点F的仰角为31°,游船朝码头方向行驶120米到达码头C,沿坡度i=1:2的斜坡CD走到点D,再向前走160米到达来福士楼底E,则来福士最高楼EF的高度约为( )(结果精确到0.1,参考数据:sin31°≈0.52,cos31°≈0.87,tan31°≈0.60)
A.301.3米 B.322.5米 C.350.2米 D.418.5米
10.如图,在中,,于点 .若,,则的长为( )
A.12 B.10 C.6 D.5
二、填空题
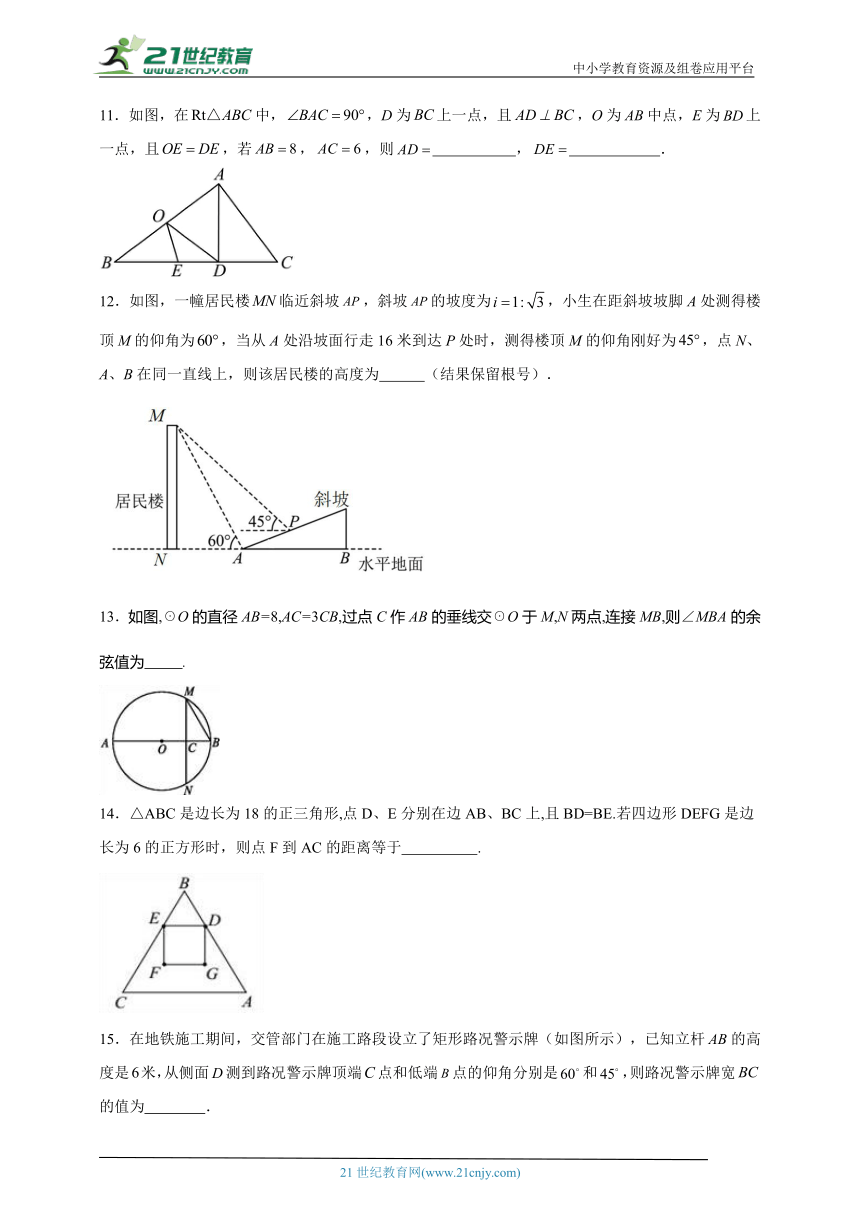
11.如图,在中,,D为上一点,且,O为中点,E为上一点,且,若,,则 , .
12.如图,一幢居民楼临近斜坡,斜坡的坡度为,小生在距斜坡坡脚A处测得楼顶M的仰角为,当从A处沿坡面行走16米到达P处时,测得楼顶M的仰角刚好为,点N、A、B在同一直线上,则该居民楼的高度为 (结果保留根号).
13.如图,☉O的直径AB=8,AC=3CB,过点C作AB的垂线交☉O于M,N两点,连接MB,则∠MBA的余弦值为 .
14.△ABC是边长为18的正三角形,点D、E分别在边AB、BC上,且BD=BE.若四边形DEFG是边长为6的正方形时,则点F到AC的距离等于 .
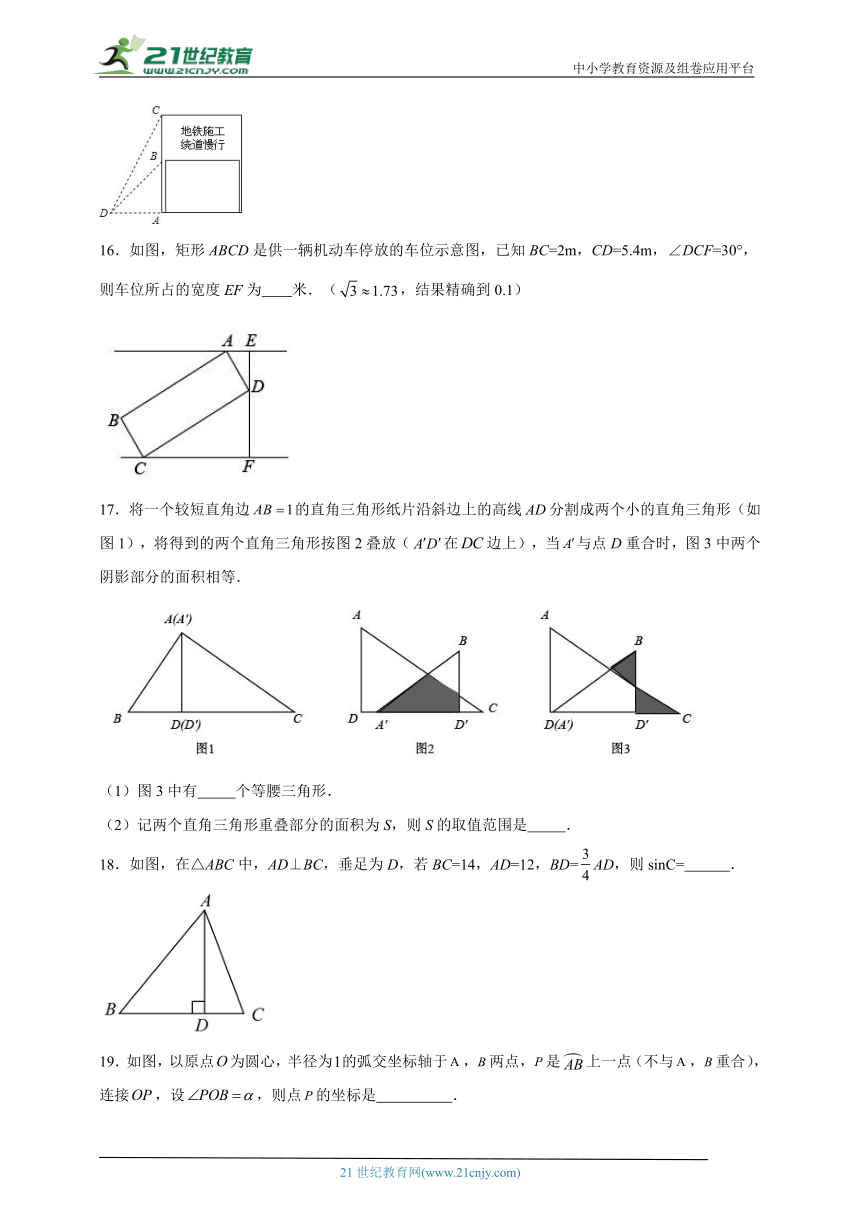
15.在地铁施工期间,交管部门在施工路段设立了矩形路况警示牌(如图所示),已知立杆的高度是米,从侧面测到路况警示牌顶端点和低端点的仰角分别是和,则路况警示牌宽的值为 .
16.如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.4m,∠DCF=30°,则车位所占的宽度EF为 米.(,结果精确到0.1)
17.将一个较短直角边的直角三角形纸片沿斜边上的高线分割成两个小的直角三角形(如图1),将得到的两个直角三角形按图2叠放(在边上),当与点D重合时,图3中两个阴影部分的面积相等.
(1)图3中有 个等腰三角形.
(2)记两个直角三角形重叠部分的面积为S,则S的取值范围是 .
18.如图,在△ABC中,AD⊥BC,垂足为D,若BC=14,AD=12,BD=AD,则sinC= .
19.如图,以原点为圆心,半径为的弧交坐标轴于,两点,是上一点(不与,重合),连接,设,则点的坐标是 .
20.如图1是一台手机支架,图2是其侧面示意图,,可分别绕点,转动,测量知,.当,转动到,时,点到的距离为 cm.(结果保留小数点后一位,参考数据:,)
三、解答题
21.图1是一台手机支架,图2是其侧面示意图,可分别绕点转动,测得.
(1)在图2中,过点作,垂足为.填空: ;
(2)求点到的距离.(结果保留小数点后一位,参考数据:)
22.如图,在 ABCD中,∠BAD的角平分线交BC于点E,交DC的延长线于点F,连接DE.
(1)求证:DA=DF;
(2)若∠ADE=∠CDE=30°,DE=2,求 ABCD的面积.
23.阅读下列材料,并解决问题.
如图1,在锐角△ABC中,∠A,∠B,∠C的对边分别是a,b,c,过点A作AD⊥BC于点D,则,,即,,于是,即.
同理有:,,所以.即在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论就可以求出其余三个未知元素.
(1)如图2,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上,求此时货轮距灯塔A的距离AB.
(2)在(1)的条件下,试求75°的正弦值.(结果保留根号)
24.如图,一艘轮船在处测得灯塔位于的北偏东方向上,轮船沿着正北方向航行20海里到达处,测得灯塔位于的北偏东方向上,测得港口位于的北偏东方向上.已知港口在灯塔的正北方向上.
(1)填空: 度, 度;
(2)求灯塔到轮船航线的距离(结果保留根号);
(3)求港口与灯塔的距离(结果保留根号).
25.(1)(问题背景)如图1,在等边中,点M是边上一点,连接,以为边作等边(A,M,N按逆时针方向排列),连接,求证:
(2)(变式探究)如图2,已知,指出图中的另外一对相似三角形并进行证明;
(3)(拓展应用)如图3,在和中,,,点D在边上,求的值.
参考答案:
1.D
2.B
3.B
4.B
5.B
6.B
7.C
8.B
9.B
10.D
11.
12.米/米
13.
14.
15.米
16.4.4
17. 3
18.
19.
20.6.3
21.(1)20
(2)10.3cm
22.(1)略;(2)4
23.(1)货轮距灯塔A的距离AB为海里;(2).
24.(1)30,45
(2)灯塔到轮船航线的距离为海里
(3)港口与灯塔的距离为海里
25.(1)略;(2);(3);
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.4解直角三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某铁路路基的横断面是一个等腰梯形(如图),若腰的坡比为2:3,路基顶宽3米,高4米,则路基的下底宽为( )
A.7米 B.9米 C.12米 D.15米
2.如图,已知第一象限的点A在反比例函数y=上,过点A作AB⊥AO交x轴于点B,∠AOB=30°,将△AOB绕点O逆时针旋转120°,点B的对应点B恰好落在反比例函数y=上,则k的值为( )
A.﹣4 B.﹣ C.﹣2 D.﹣
3.在△ABC中,∠C=90°,∠BAC=30°,AD是中线,则tan∠CDA的值为( )
A.3 B.2 C. D.
4.在△ABC中,∠C=90°,sinB=,b=,则a等于( )
A. B.1 C.2 D.3
5.如图1,某小区入口处安装“曲臂杆”,OA⊥AB,OA=1米,点O是臂杆转动的支点,点C是曲臂杆两段的连接点,曲臂杆CD部分始终与AB平行.如图2,曲臂杆初始位置时O、C、D三点共线,当曲臂杆升高到OE时,∠AOE=121°,点E到AB的距离是1.7米,当曲臂杆升高到OF时,∠AOF=156°,则点F到AB的距离是(结果精确到0.1米,参考数据:sin31°≈0.5,sin66°≈0.9)( )
A.2.0米 B.2.3米 C.2.4米 D.2.6米
6.如图,某学校后坡有一个凉亭在点处,通往凉亭要走两段坡度不一样的阶梯和部分的坡角为,部分的坡度(或坡比).已知和两段阶梯的台阶数量相同,每个台阶的高度也相同,若第一段坡长,则第二段坡长约为( )(参考数据: )
A. B. C. D.
7.如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达B处,又测得信号塔顶端C的仰角为45°,CE⊥AB于点E,E、B、A在一条直线上.则信号塔CD的高度为( )
A.20米 B.(20-8)米 C.(20-28)米 D.(20-20)米
8.如图,在平面直角坐标系中,一次函数和的图象分别为直线,与y轴交于点A,过A点作x轴的平行线与交于,过作y轴的平行线与交于A1,过作x轴的平行线与交于,…,依次进行下去,则的长为( )
A. B. C. D.
9.某游客乘坐“金碧皇宫号游船”在长江和嘉陵江的交汇处A点,测得来福土最高楼顶点F的仰角为45°,此时他头项正上方146米的点B处有架航拍无人机测得来福士最高楼顶点F的仰角为31°,游船朝码头方向行驶120米到达码头C,沿坡度i=1:2的斜坡CD走到点D,再向前走160米到达来福士楼底E,则来福士最高楼EF的高度约为( )(结果精确到0.1,参考数据:sin31°≈0.52,cos31°≈0.87,tan31°≈0.60)
A.301.3米 B.322.5米 C.350.2米 D.418.5米
10.如图,在中,,于点 .若,,则的长为( )
A.12 B.10 C.6 D.5
二、填空题
11.如图,在中,,D为上一点,且,O为中点,E为上一点,且,若,,则 , .
12.如图,一幢居民楼临近斜坡,斜坡的坡度为,小生在距斜坡坡脚A处测得楼顶M的仰角为,当从A处沿坡面行走16米到达P处时,测得楼顶M的仰角刚好为,点N、A、B在同一直线上,则该居民楼的高度为 (结果保留根号).
13.如图,☉O的直径AB=8,AC=3CB,过点C作AB的垂线交☉O于M,N两点,连接MB,则∠MBA的余弦值为 .
14.△ABC是边长为18的正三角形,点D、E分别在边AB、BC上,且BD=BE.若四边形DEFG是边长为6的正方形时,则点F到AC的距离等于 .
15.在地铁施工期间,交管部门在施工路段设立了矩形路况警示牌(如图所示),已知立杆的高度是米,从侧面测到路况警示牌顶端点和低端点的仰角分别是和,则路况警示牌宽的值为 .
16.如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.4m,∠DCF=30°,则车位所占的宽度EF为 米.(,结果精确到0.1)
17.将一个较短直角边的直角三角形纸片沿斜边上的高线分割成两个小的直角三角形(如图1),将得到的两个直角三角形按图2叠放(在边上),当与点D重合时,图3中两个阴影部分的面积相等.
(1)图3中有 个等腰三角形.
(2)记两个直角三角形重叠部分的面积为S,则S的取值范围是 .
18.如图,在△ABC中,AD⊥BC,垂足为D,若BC=14,AD=12,BD=AD,则sinC= .
19.如图,以原点为圆心,半径为的弧交坐标轴于,两点,是上一点(不与,重合),连接,设,则点的坐标是 .
20.如图1是一台手机支架,图2是其侧面示意图,,可分别绕点,转动,测量知,.当,转动到,时,点到的距离为 cm.(结果保留小数点后一位,参考数据:,)
三、解答题
21.图1是一台手机支架,图2是其侧面示意图,可分别绕点转动,测得.
(1)在图2中,过点作,垂足为.填空: ;
(2)求点到的距离.(结果保留小数点后一位,参考数据:)
22.如图,在 ABCD中,∠BAD的角平分线交BC于点E,交DC的延长线于点F,连接DE.
(1)求证:DA=DF;
(2)若∠ADE=∠CDE=30°,DE=2,求 ABCD的面积.
23.阅读下列材料,并解决问题.
如图1,在锐角△ABC中,∠A,∠B,∠C的对边分别是a,b,c,过点A作AD⊥BC于点D,则,,即,,于是,即.
同理有:,,所以.即在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论就可以求出其余三个未知元素.
(1)如图2,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上,求此时货轮距灯塔A的距离AB.
(2)在(1)的条件下,试求75°的正弦值.(结果保留根号)
24.如图,一艘轮船在处测得灯塔位于的北偏东方向上,轮船沿着正北方向航行20海里到达处,测得灯塔位于的北偏东方向上,测得港口位于的北偏东方向上.已知港口在灯塔的正北方向上.
(1)填空: 度, 度;
(2)求灯塔到轮船航线的距离(结果保留根号);
(3)求港口与灯塔的距离(结果保留根号).
25.(1)(问题背景)如图1,在等边中,点M是边上一点,连接,以为边作等边(A,M,N按逆时针方向排列),连接,求证:
(2)(变式探究)如图2,已知,指出图中的另外一对相似三角形并进行证明;
(3)(拓展应用)如图3,在和中,,,点D在边上,求的值.
参考答案:
1.D
2.B
3.B
4.B
5.B
6.B
7.C
8.B
9.B
10.D
11.
12.米/米
13.
14.
15.米
16.4.4
17. 3
18.
19.
20.6.3
21.(1)20
(2)10.3cm
22.(1)略;(2)4
23.(1)货轮距灯塔A的距离AB为海里;(2).
24.(1)30,45
(2)灯塔到轮船航线的距离为海里
(3)港口与灯塔的距离为海里
25.(1)略;(2);(3);
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
