26.3 实践与探索 分层练习(含答案)
文档属性
| 名称 | 26.3 实践与探索 分层练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 947.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 15:35:59 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
26.3实践与探索
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个小球以的初速度向上竖直弹出,它在空中的高度与时间满足关系式,当小球的高度为时,t为( )
A.1s B.2s C.1s或2s D.以上都不对
2.九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.方案1或方案2
3.点C为线段AB上的一个动点,,分别以AC和CB为一边作等边三角形,用S表示这两个等边三角形的面积之和,下列判断正确的是( )
A.当C为AB的三等分点时,S最小 B.当C是AB的中点时,S最大
C.当C为AB的三等分点时,S最大 D.当C是AB的中点时,S最小
4.如图,在中,,动点P从点A出发,以每秒1个单位长度的速度沿线段匀速运动,当点P运动到点B时,停止运动,过点P作交于点Q,将沿直线折叠得到,设动点P的运动时间为t秒,与重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B. C. D.
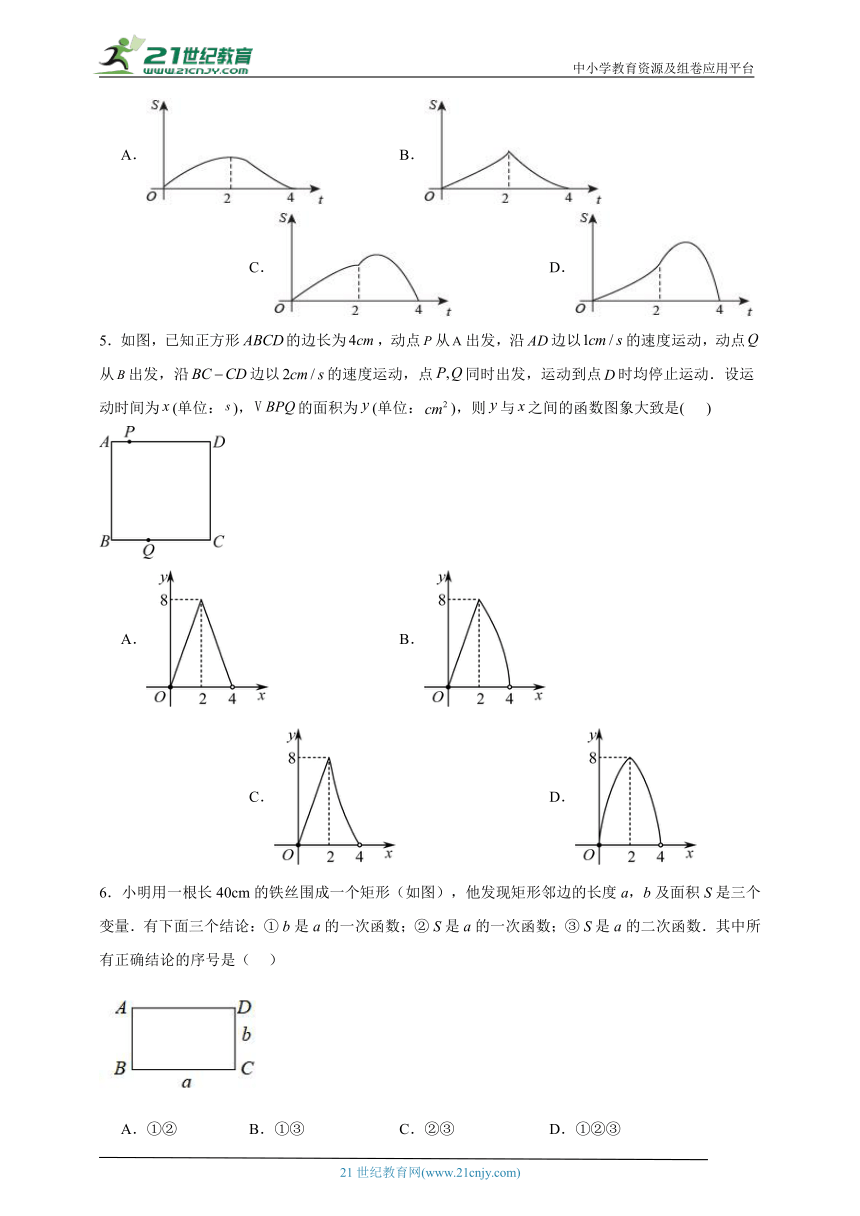
5.如图,已知正方形的边长为,动点从出发,沿边以的速度运动,动点从出发,沿边以的速度运动,点同时出发,运动到点时均停止运动.设运动时间为(单位:),的面积为(单位:),则与之间的函数图象大致是( )
A. B. C. D.
6.小明用一根长40cm的铁丝围成一个矩形(如图),他发现矩形邻边的长度a,b及面积S是三个变量.有下面三个结论:① b是a的一次函数;② S是a的一次函数;③ S是a的二次函数.其中所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
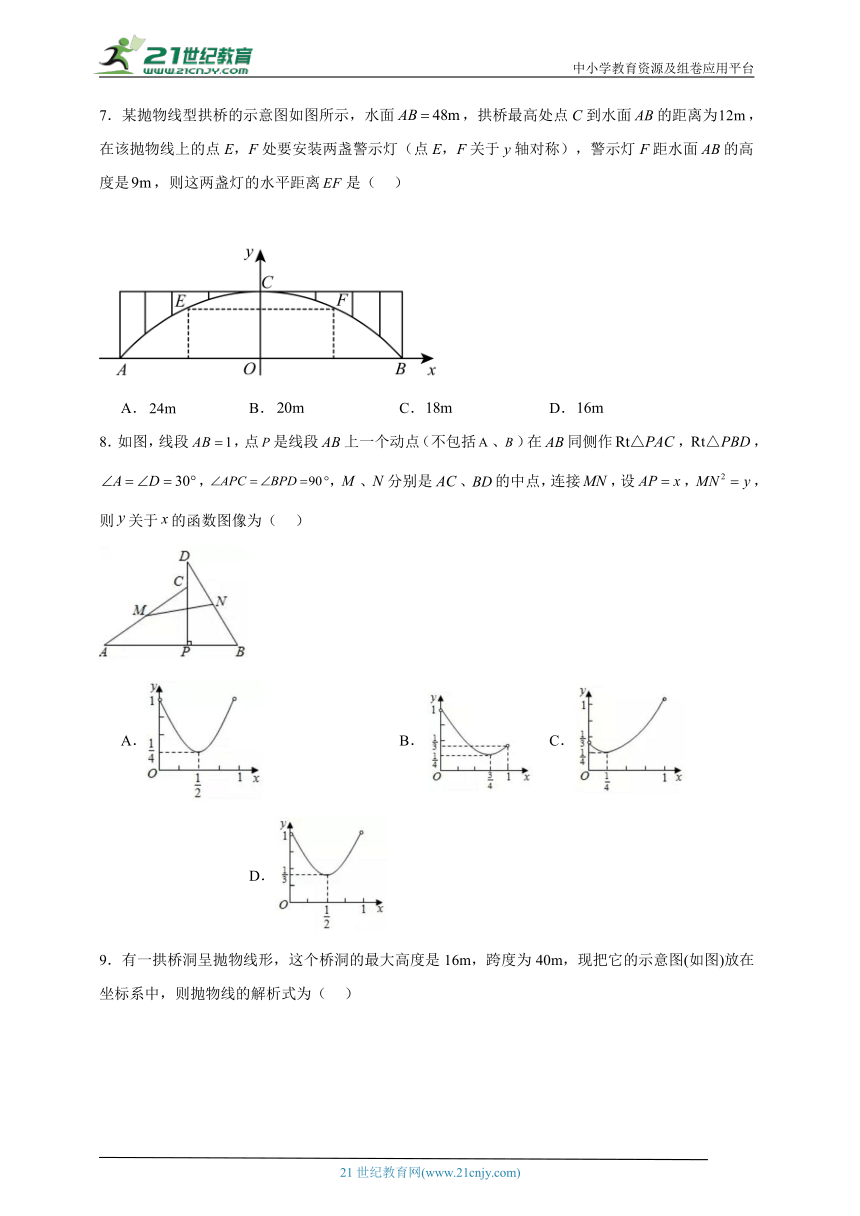
7.某抛物线型拱桥的示意图如图所示,水面,拱桥最高处点C到水面的距离为,在该抛物线上的点E,F处要安装两盏警示灯(点E,F关于y轴对称),警示灯F距水面的高度是,则这两盏灯的水平距离是( )
A. B. C. D.
8.如图,线段,点是线段上一个动点(不包括、)在同侧作,,,,、分别是、的中点,连接,设,,则关于的函数图像为( )
A. B. C. D.
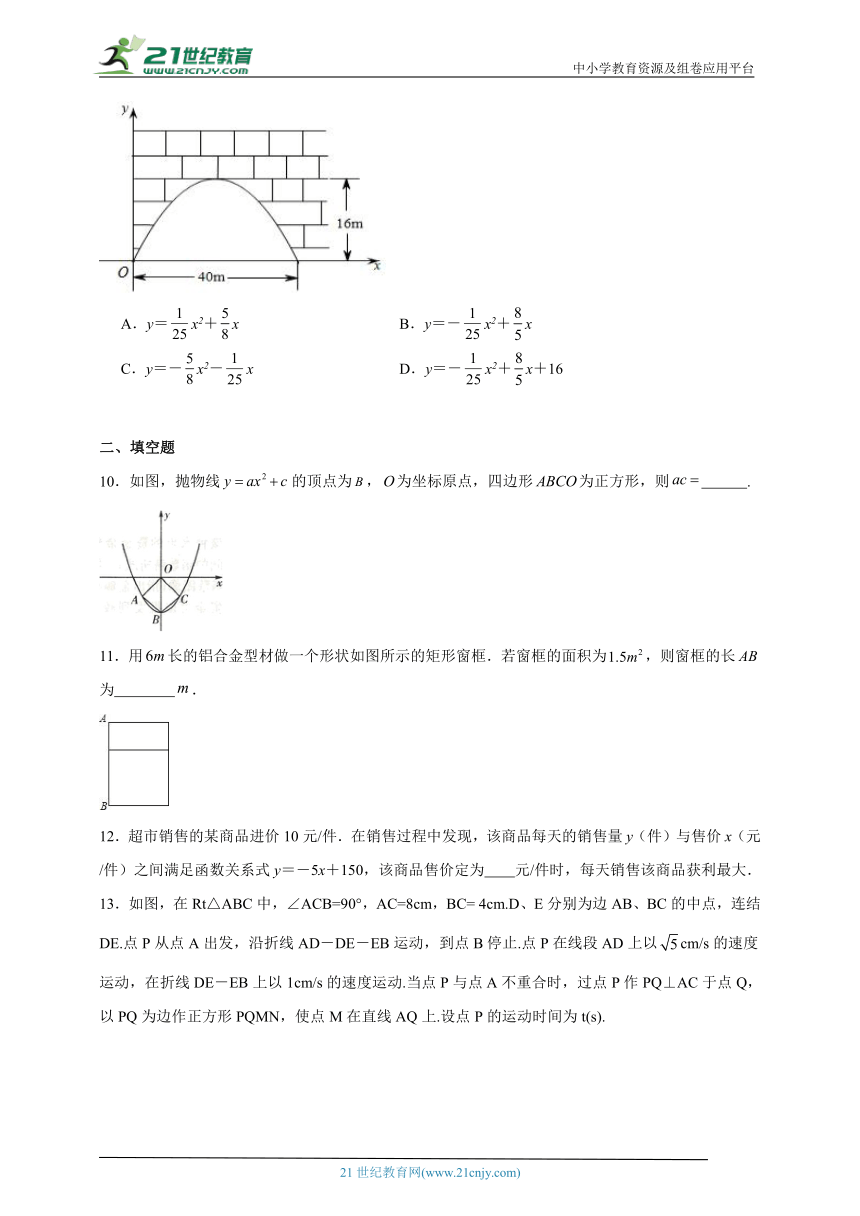
9.有一拱桥洞呈抛物线形,这个桥洞的最大高度是16m,跨度为40m,现把它的示意图(如图)放在坐标系中,则抛物线的解析式为( )
A.y=x2+x B.y=-x2+x
C.y=-x2-x D.y=-x2+x+16
二、填空题
10.如图,抛物线的顶点为,为坐标原点,四边形为正方形,则 .
11.用长的铝合金型材做一个形状如图所示的矩形窗框.若窗框的面积为,则窗框的长为 .
12.超市销售的某商品进价10元/件.在销售过程中发现,该商品每天的销售量y(件)与售价x(元/件)之间满足函数关系式y=-5x+150,该商品售价定为 元/件时,每天销售该商品获利最大.
13.如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC= 4cm.D、E分别为边AB、BC的中点,连结DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在线段AD上以cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在直线AQ上.设点P的运动时间为t(s).
(1)当点P在线段DE上运动时,线段DP的长为 cm(用含t的代数式表示)
(2)当点N落在AB边上时,求t的值.
(3)当正方形PQMN与△ABC重叠部分的面积为S(cm2),求S与t的函数关系式.
(4)连结CD.当点N与点D重合时,有一点H从点M出发,在线段MN上以2.5cm/s的速度沿M-N-M连续做往返运动,直至点P与点E重合时,点H停止往返运动;当点P在线段EB上运动时,点H始终在线段MN的中点处.直接写出在点P的整个运动过程中,点H落在线段CD上时t的值(或取值范围).
14.教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为,由此可知铅球推出的距离是 m.
15.为庆祝嫦娥五号登月成功,某工艺厂生产了一款纪念品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就多售出5件,但要求销售单价不得低于成本.则该工艺厂将每件的销售价定为 元时,可使每天所获销售利润最大.
16.如图,在第一象限内作与x轴的夹角为30°的射线OC,在射线OC上取点A,过点A作AH⊥x轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P,O,Q为顶点的三角形与△AOH全等,则符合条件的点A有 个.
17.如图,抛物线与函数的图象在第一象限交点的横坐标为4,点在抛物线上,点在正比例函数的图象上,当时,的最大值为 .
18.校运动会上,小明参加铅球比赛,若某次试掷,铅球飞行的高度与水平距离之间的函数关系式为,小明这次试掷的成绩为 ,铅球出手时的高度是 .
19.生物学研究表明,在一定的温度范围内,酶的活性会随温度的升高逐渐增强;在最适温度时,酶的活性最强;超过一定温度范围,酶的活性又随温度的开高逐渐减弱,甚至会失去活性现已知某种酶的活性值(单位:)与温度(单位:)的关系可以近似用二次函数来表示,则当温度为最适宜温度时,该种酶的活性值为 .
三、解答题
20.如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点
M从点A出发,沿AC的方向匀速运动,速度为2cm/s;同时直线PQ由点B出发,沿BA
的方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交
BC于点Q、交BD于点F.连接PM,设运动时间为ts(0<t<5).
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为ycm2,求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PQCM=S△ABC?若存在,求出t的值;若不存在,说明理由;
(4)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
21.一座古老的石拱桥的侧面形状可以用如图抛物线刻画,OB为水平面,距O点水平距离1米的AC处立着一个水泥柱加固桥梁,拱桥在距O点水平距离3米处达到最大高度9米.
(1)求此抛物线的解析式.
(2)一只蜻蜓落在水泥柱左侧的拱桥内壁P处,且它飞到C点和A点的距离相同,求这只蜻蜓到水泥柱的水平距离.
22.明月山景区在2021年寒假期间,共接待游客达200万人次,预计在2023年寒假期间,将接待游客达288万人次.
(1)求景区2021至2023年寒假期间接待游客人次的平均增长率;
(2)景区一奶茶店销售一款奶茶,每杯成本价为10元,根据销售经验,在旅游旺季,若每杯定价24元,则平均每天可销售200杯,若每杯价格降低1元,则平均每天可多销售20杯,店家决定进行降价促销活动,当每杯售价定为多少元时,利润最大?
23.如图,已知二次函数(其中0<m<1)的图像与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC.
(1)∠ABC的度数为 °;
(2)求P点坐标(用含m的代数式表示);
(3)在坐标轴上是否存在点Q(与原点O不重合),使得以Q、B、C为顶点的三角形与△PAC相似,且线段PQ的长度最小?如果存在,求出所有满足条件的点Q的坐标;如果不存在,请说明理由.
24.如图,有一块矩形铁皮(厚度不计),长10分米,宽8分米,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒.
(1)若无盖方盒的底面积为48平方分米,那么铁皮各角应切去边长是多少分米的正方形?
(2)若要求制作的无盖方盒的底面长不大于底面宽的2倍,并将无盖方盒内部进行防锈处理,侧面每平方分米的防锈处理费用为0.5元,底面每平方分米的防锈处理费用为2元,问铁皮各角切去边长是多少分米的正方形时,总费用最低?最低费用为多少元?
参考答案:
1.C
2.C
3.D
4.D
5.B
6.B
7.A
8.B
9.B
10.-2
11.
12.20
13.(1)t – 2(2)4(3)
14.()
15.80
16.4
17.
18.
19.240
20.(1);(2);(3);(4)
21.(1)y=-(x+3)2+9;(2)米
22.(1)明月山景区2021至2023年寒假期间接待游客人次的平均增长率是20%
(2)当每杯售价定为22元时,利润最大为2880元
23.(1)45,(2)(3)存在,当Q点坐标为(,0)或(0,)时,PQ的长度最小
24.(1)铁皮各角应切去边长是1分米的正方形;
(2)当铁皮各角切去边长是3分米的正方形时,总费用最低,最低费用为20元;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
26.3实践与探索
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个小球以的初速度向上竖直弹出,它在空中的高度与时间满足关系式,当小球的高度为时,t为( )
A.1s B.2s C.1s或2s D.以上都不对
2.九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.方案1或方案2
3.点C为线段AB上的一个动点,,分别以AC和CB为一边作等边三角形,用S表示这两个等边三角形的面积之和,下列判断正确的是( )
A.当C为AB的三等分点时,S最小 B.当C是AB的中点时,S最大
C.当C为AB的三等分点时,S最大 D.当C是AB的中点时,S最小
4.如图,在中,,动点P从点A出发,以每秒1个单位长度的速度沿线段匀速运动,当点P运动到点B时,停止运动,过点P作交于点Q,将沿直线折叠得到,设动点P的运动时间为t秒,与重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B. C. D.
5.如图,已知正方形的边长为,动点从出发,沿边以的速度运动,动点从出发,沿边以的速度运动,点同时出发,运动到点时均停止运动.设运动时间为(单位:),的面积为(单位:),则与之间的函数图象大致是( )
A. B. C. D.
6.小明用一根长40cm的铁丝围成一个矩形(如图),他发现矩形邻边的长度a,b及面积S是三个变量.有下面三个结论:① b是a的一次函数;② S是a的一次函数;③ S是a的二次函数.其中所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
7.某抛物线型拱桥的示意图如图所示,水面,拱桥最高处点C到水面的距离为,在该抛物线上的点E,F处要安装两盏警示灯(点E,F关于y轴对称),警示灯F距水面的高度是,则这两盏灯的水平距离是( )
A. B. C. D.
8.如图,线段,点是线段上一个动点(不包括、)在同侧作,,,,、分别是、的中点,连接,设,,则关于的函数图像为( )
A. B. C. D.
9.有一拱桥洞呈抛物线形,这个桥洞的最大高度是16m,跨度为40m,现把它的示意图(如图)放在坐标系中,则抛物线的解析式为( )
A.y=x2+x B.y=-x2+x
C.y=-x2-x D.y=-x2+x+16
二、填空题
10.如图,抛物线的顶点为,为坐标原点,四边形为正方形,则 .
11.用长的铝合金型材做一个形状如图所示的矩形窗框.若窗框的面积为,则窗框的长为 .
12.超市销售的某商品进价10元/件.在销售过程中发现,该商品每天的销售量y(件)与售价x(元/件)之间满足函数关系式y=-5x+150,该商品售价定为 元/件时,每天销售该商品获利最大.
13.如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC= 4cm.D、E分别为边AB、BC的中点,连结DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在线段AD上以cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在直线AQ上.设点P的运动时间为t(s).
(1)当点P在线段DE上运动时,线段DP的长为 cm(用含t的代数式表示)
(2)当点N落在AB边上时,求t的值.
(3)当正方形PQMN与△ABC重叠部分的面积为S(cm2),求S与t的函数关系式.
(4)连结CD.当点N与点D重合时,有一点H从点M出发,在线段MN上以2.5cm/s的速度沿M-N-M连续做往返运动,直至点P与点E重合时,点H停止往返运动;当点P在线段EB上运动时,点H始终在线段MN的中点处.直接写出在点P的整个运动过程中,点H落在线段CD上时t的值(或取值范围).
14.教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为,由此可知铅球推出的距离是 m.
15.为庆祝嫦娥五号登月成功,某工艺厂生产了一款纪念品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就多售出5件,但要求销售单价不得低于成本.则该工艺厂将每件的销售价定为 元时,可使每天所获销售利润最大.
16.如图,在第一象限内作与x轴的夹角为30°的射线OC,在射线OC上取点A,过点A作AH⊥x轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P,O,Q为顶点的三角形与△AOH全等,则符合条件的点A有 个.
17.如图,抛物线与函数的图象在第一象限交点的横坐标为4,点在抛物线上,点在正比例函数的图象上,当时,的最大值为 .
18.校运动会上,小明参加铅球比赛,若某次试掷,铅球飞行的高度与水平距离之间的函数关系式为,小明这次试掷的成绩为 ,铅球出手时的高度是 .
19.生物学研究表明,在一定的温度范围内,酶的活性会随温度的升高逐渐增强;在最适温度时,酶的活性最强;超过一定温度范围,酶的活性又随温度的开高逐渐减弱,甚至会失去活性现已知某种酶的活性值(单位:)与温度(单位:)的关系可以近似用二次函数来表示,则当温度为最适宜温度时,该种酶的活性值为 .
三、解答题
20.如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点
M从点A出发,沿AC的方向匀速运动,速度为2cm/s;同时直线PQ由点B出发,沿BA
的方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交
BC于点Q、交BD于点F.连接PM,设运动时间为ts(0<t<5).
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为ycm2,求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PQCM=S△ABC?若存在,求出t的值;若不存在,说明理由;
(4)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
21.一座古老的石拱桥的侧面形状可以用如图抛物线刻画,OB为水平面,距O点水平距离1米的AC处立着一个水泥柱加固桥梁,拱桥在距O点水平距离3米处达到最大高度9米.
(1)求此抛物线的解析式.
(2)一只蜻蜓落在水泥柱左侧的拱桥内壁P处,且它飞到C点和A点的距离相同,求这只蜻蜓到水泥柱的水平距离.
22.明月山景区在2021年寒假期间,共接待游客达200万人次,预计在2023年寒假期间,将接待游客达288万人次.
(1)求景区2021至2023年寒假期间接待游客人次的平均增长率;
(2)景区一奶茶店销售一款奶茶,每杯成本价为10元,根据销售经验,在旅游旺季,若每杯定价24元,则平均每天可销售200杯,若每杯价格降低1元,则平均每天可多销售20杯,店家决定进行降价促销活动,当每杯售价定为多少元时,利润最大?
23.如图,已知二次函数(其中0<m<1)的图像与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC.
(1)∠ABC的度数为 °;
(2)求P点坐标(用含m的代数式表示);
(3)在坐标轴上是否存在点Q(与原点O不重合),使得以Q、B、C为顶点的三角形与△PAC相似,且线段PQ的长度最小?如果存在,求出所有满足条件的点Q的坐标;如果不存在,请说明理由.
24.如图,有一块矩形铁皮(厚度不计),长10分米,宽8分米,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒.
(1)若无盖方盒的底面积为48平方分米,那么铁皮各角应切去边长是多少分米的正方形?
(2)若要求制作的无盖方盒的底面长不大于底面宽的2倍,并将无盖方盒内部进行防锈处理,侧面每平方分米的防锈处理费用为0.5元,底面每平方分米的防锈处理费用为2元,问铁皮各角切去边长是多少分米的正方形时,总费用最低?最低费用为多少元?
参考答案:
1.C
2.C
3.D
4.D
5.B
6.B
7.A
8.B
9.B
10.-2
11.
12.20
13.(1)t – 2(2)4(3)
14.()
15.80
16.4
17.
18.
19.240
20.(1);(2);(3);(4)
21.(1)y=-(x+3)2+9;(2)米
22.(1)明月山景区2021至2023年寒假期间接待游客人次的平均增长率是20%
(2)当每杯售价定为22元时,利润最大为2880元
23.(1)45,(2)(3)存在,当Q点坐标为(,0)或(0,)时,PQ的长度最小
24.(1)铁皮各角应切去边长是1分米的正方形;
(2)当铁皮各角切去边长是3分米的正方形时,总费用最低,最低费用为20元;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
