沪教版三年级下册数学7.8《数学广场——放苹果》课件(共14张PPT)
文档属性
| 名称 | 沪教版三年级下册数学7.8《数学广场——放苹果》课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
《数学广场——放苹果》
沪教版三年级下册
放苹果。3个苹果放入2个抽屉。不管怎么放,至少有一个抽屉里的苹果不止一个。
问题(1)导入
过程讲解
用不同的方法证明题中的观点。
方法一 实际操作证明。
得出:一共有4种情况,每种情况中都一定至少有一个抽屉里
的苹果不止一个,即至少有2个苹果。
把3(苹果个数)分拆成2(抽屉数量)个加数。如下所示:
用不同的方法证明题中的观点。
方法二 从数的分解的角度进行验证。
(0,3)
(1,2)
(2,1)
(3,0)
3分拆成2个加数
4种分法中的2个数,至少有一个数不小于2,即至少有一个抽屉里有2个或2个以上的苹果。
将3个苹果按抽屉的个数平均分成2份,再根据剩下的苹果判断分配的结果。
用不同的方法证明题中的观点。
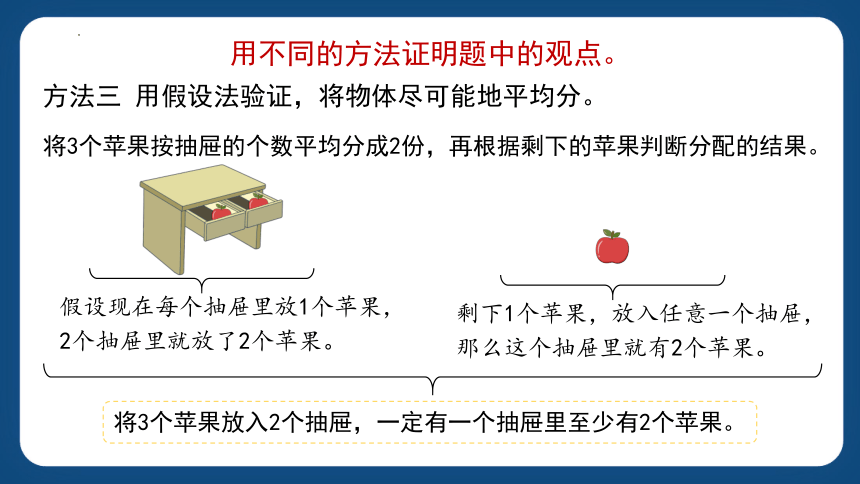
方法三 用假设法验证,将物体尽可能地平均分。
假设现在每个抽屉里放1个苹果,2个抽屉里就放了2个苹果。
剩下1个苹果,放入任意一个抽屉,那么这个抽屉里就有2个苹果。
将3个苹果放入2个抽屉,一定有一个抽屉里至少有2个苹果。
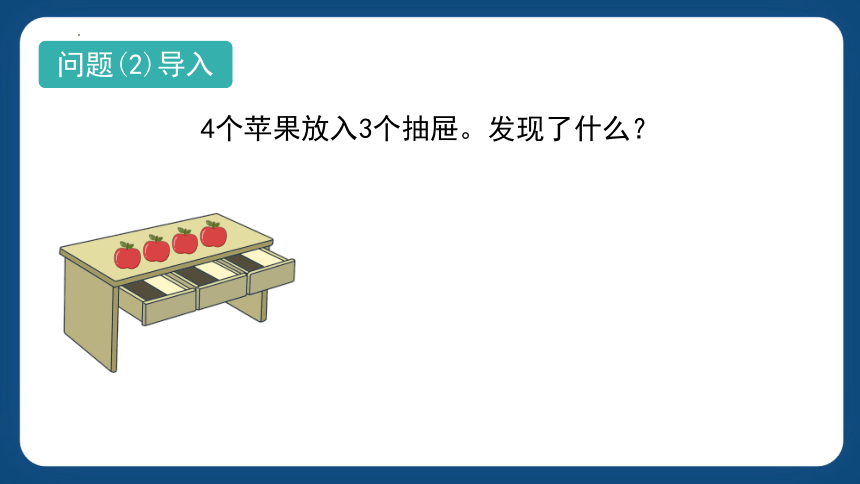
4个苹果放入3个抽屉。发现了什么?
问题(2)导入
过程讲解
1.具体解题过程。
方法一 借助图示及数的分拆解题。
0 0 4
0 1 3
0 2 2
0 3 1
0 4 0
1 0 3
1 1 2
1 2 1
1 3 0
2 0 2
2 1 1
2 2 0
3 0 1
3 1 0
4 0 0
15种分法中的3个数,至少有一个数不小于2,即至少有一个抽屉里有2个或2个以上的苹果。
1.具体解题过程。
方法二 用假设法解题。
假设现在每个抽屉里放1个苹果,3个抽屉里就放了3个苹果。
剩下1个苹果,放入任意一个抽屉,那么这个抽屉里就有2个苹果。
将4个苹果放入3个抽屉,一定有一个抽屉里至少有2个苹果。
2.理解“抽屉原理”。
(1)明确“抽屉原理”。
像上面这样的问题称为“抽屉问题”,它里面蕴涵的数学原理就叫做“抽屉原理”。在这里,“3个、4个苹果”就是“3个、4个被分放的物体”。
(2)初步了解“抽屉原理”。
将3个苹果放入2个抽屉,将4个苹果放入3个抽屉,即被分放的物体个数比抽屉个数多1个。得出结论:至少有一个抽屉里有2个或2个以上的物体。
2.理解“抽屉原理”。
(3) 构建“抽屉原理”的模型,理解“抽屉原理”。
苹果个数 抽屉个数 分配结果
5 4 总有一个抽屉里至少放进2个苹果
6 5 总有一个抽屉里至少放进2个苹果
7 6 总有一个抽屉里至少放进2个苹果
发现 只要苹果个数比抽屉个数多1个,就总有一个抽屉里至少放进2个苹果。
“抽屉原理”:将n+1个物体放入n个抽屉中,至少有一个抽屉里有2个或2个以上的物体。
总 结
1.实验小学三年级美术组有14名学生,至少有几名学生
的生日在同一个月份?
练习
2.如果一个班同学的生日都在6月份,并且至少有2人的
生日在同一天,那么这个班至少有多少人?
3.盒子里有质地、大小完全相同的红球和黄球各7个,要
想摸出的球一定有2个是同色的,至少要摸出几个球?
《数学广场——放苹果》
沪教版三年级下册
放苹果。3个苹果放入2个抽屉。不管怎么放,至少有一个抽屉里的苹果不止一个。
问题(1)导入
过程讲解
用不同的方法证明题中的观点。
方法一 实际操作证明。
得出:一共有4种情况,每种情况中都一定至少有一个抽屉里
的苹果不止一个,即至少有2个苹果。
把3(苹果个数)分拆成2(抽屉数量)个加数。如下所示:
用不同的方法证明题中的观点。
方法二 从数的分解的角度进行验证。
(0,3)
(1,2)
(2,1)
(3,0)
3分拆成2个加数
4种分法中的2个数,至少有一个数不小于2,即至少有一个抽屉里有2个或2个以上的苹果。
将3个苹果按抽屉的个数平均分成2份,再根据剩下的苹果判断分配的结果。
用不同的方法证明题中的观点。
方法三 用假设法验证,将物体尽可能地平均分。
假设现在每个抽屉里放1个苹果,2个抽屉里就放了2个苹果。
剩下1个苹果,放入任意一个抽屉,那么这个抽屉里就有2个苹果。
将3个苹果放入2个抽屉,一定有一个抽屉里至少有2个苹果。
4个苹果放入3个抽屉。发现了什么?
问题(2)导入
过程讲解
1.具体解题过程。
方法一 借助图示及数的分拆解题。
0 0 4
0 1 3
0 2 2
0 3 1
0 4 0
1 0 3
1 1 2
1 2 1
1 3 0
2 0 2
2 1 1
2 2 0
3 0 1
3 1 0
4 0 0
15种分法中的3个数,至少有一个数不小于2,即至少有一个抽屉里有2个或2个以上的苹果。
1.具体解题过程。
方法二 用假设法解题。
假设现在每个抽屉里放1个苹果,3个抽屉里就放了3个苹果。
剩下1个苹果,放入任意一个抽屉,那么这个抽屉里就有2个苹果。
将4个苹果放入3个抽屉,一定有一个抽屉里至少有2个苹果。
2.理解“抽屉原理”。
(1)明确“抽屉原理”。
像上面这样的问题称为“抽屉问题”,它里面蕴涵的数学原理就叫做“抽屉原理”。在这里,“3个、4个苹果”就是“3个、4个被分放的物体”。
(2)初步了解“抽屉原理”。
将3个苹果放入2个抽屉,将4个苹果放入3个抽屉,即被分放的物体个数比抽屉个数多1个。得出结论:至少有一个抽屉里有2个或2个以上的物体。
2.理解“抽屉原理”。
(3) 构建“抽屉原理”的模型,理解“抽屉原理”。
苹果个数 抽屉个数 分配结果
5 4 总有一个抽屉里至少放进2个苹果
6 5 总有一个抽屉里至少放进2个苹果
7 6 总有一个抽屉里至少放进2个苹果
发现 只要苹果个数比抽屉个数多1个,就总有一个抽屉里至少放进2个苹果。
“抽屉原理”:将n+1个物体放入n个抽屉中,至少有一个抽屉里有2个或2个以上的物体。
总 结
1.实验小学三年级美术组有14名学生,至少有几名学生
的生日在同一个月份?
练习
2.如果一个班同学的生日都在6月份,并且至少有2人的
生日在同一天,那么这个班至少有多少人?
3.盒子里有质地、大小完全相同的红球和黄球各7个,要
想摸出的球一定有2个是同色的,至少要摸出几个球?
