第五章三角形（复习课）

课件35张PPT。第五章 三角形－－复习课一、三角形的边、角及主要线段１、三角形的三边之间的关系：两边之和大于第三边，两边之差小于第三边２、三角形的三个内角之间的关系：三角形的内角和为１８００3、三角形的主要线段有哪些？角平分线、中线、高线练一练：
1、下列每组分别是三根小木棒的长度，用它们能摆成三角形吗？（单位：厘米。填“能”或“不能”)
（1）3，4，5（ ）
（2）8，7，15（ ）
（3）13，12，20（ ）
（4）5，5，11（ ）不能不能能能直角三角形钝角三角形2、三角形按内角的大小分为三类：①锐角三角形；
②直角三角形；③钝角三角形。根据下列条件判断它们
是什么三角形？
（1）三个内角的度数是1:2:3（ ）
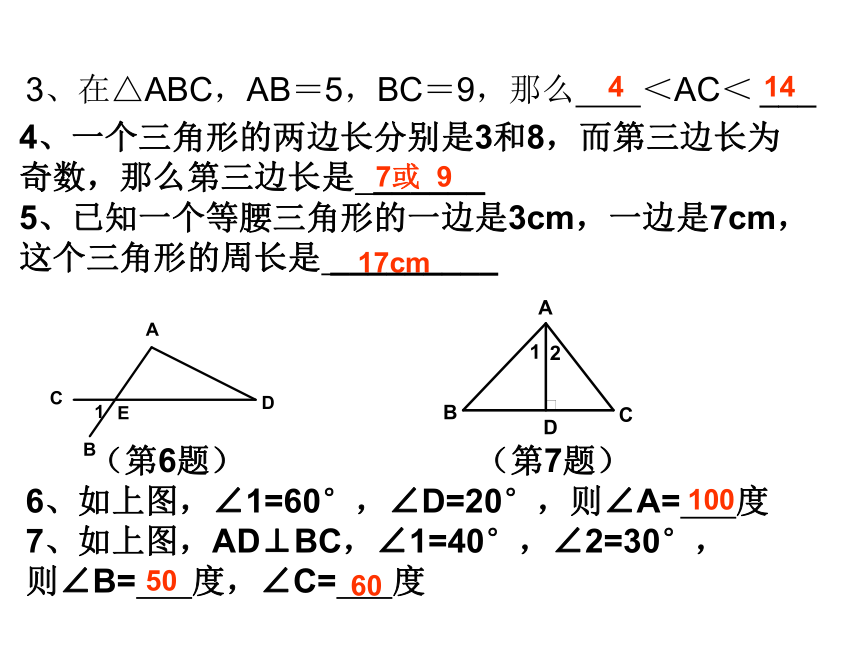
（2）两个内角是50°和30°（ ）3、在△ABC，AB＝5，BC＝9，那么 ＜AC＜ ___
（第6题） （第7题）
6、如上图，∠1=60°，∠D=20°，则∠A= 度
7、如上图，AD⊥BC，∠1=40°，∠2=30°，
则∠B= 度，∠C= 度4147或 917cm10050604、一个三角形的两边长分别是3和8，而第三边长为
奇数，那么第三边长是 ______
5、已知一个等腰三角形的一边是3cm，一边是7cm，
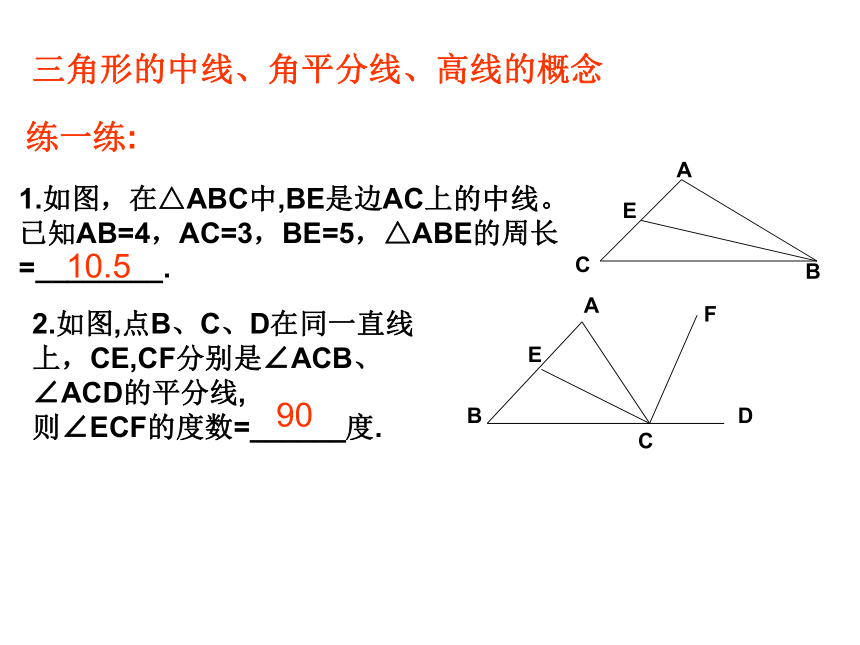
这个三角形的周长是 _________ 1.如图，在△ABC中,BE是边AC上的中线。已知AB=4，AC=3，BE=5，△ABE的周长=________.2.如图,点B、C、D在同一直线上，CE,CF分别是∠ACB、∠ACD的平分线,
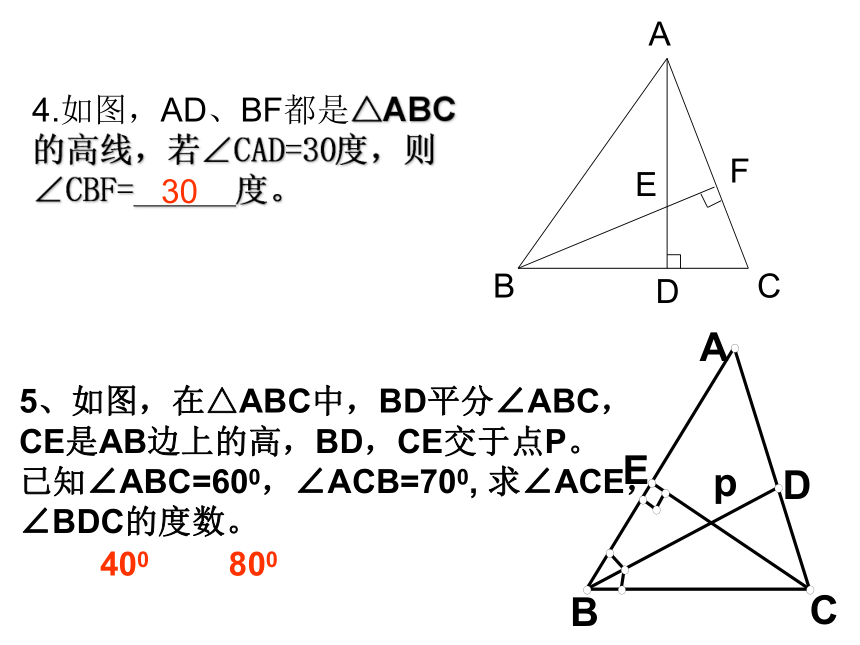
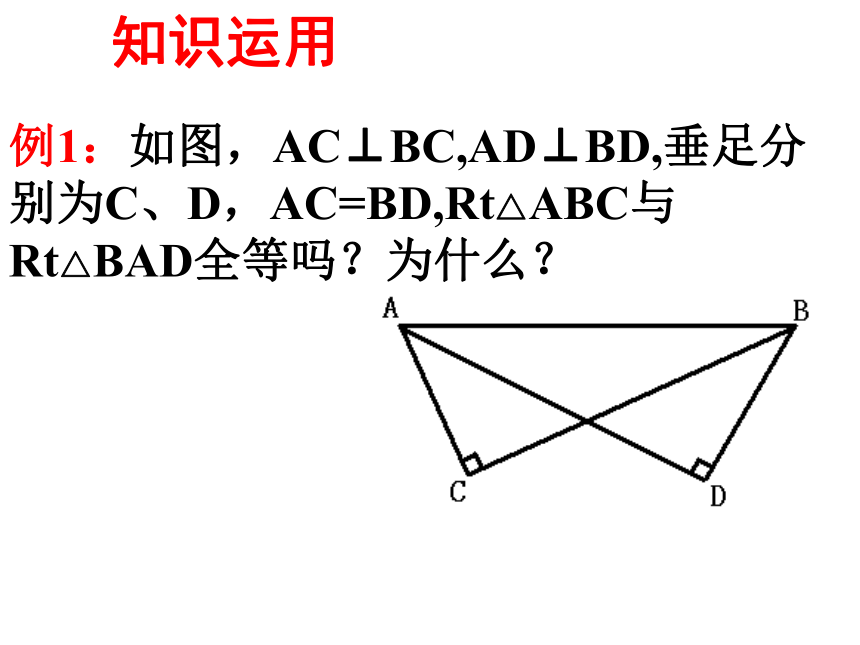
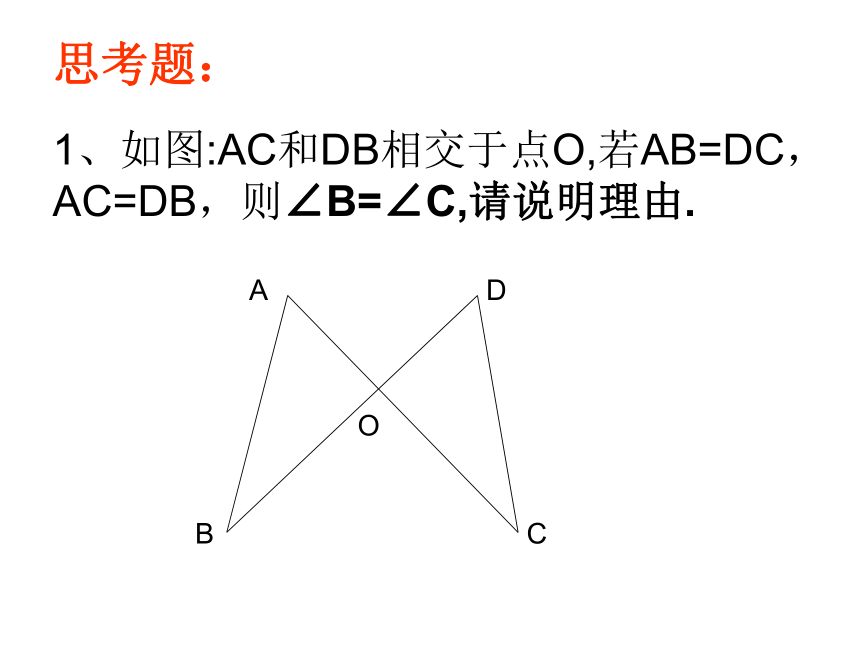
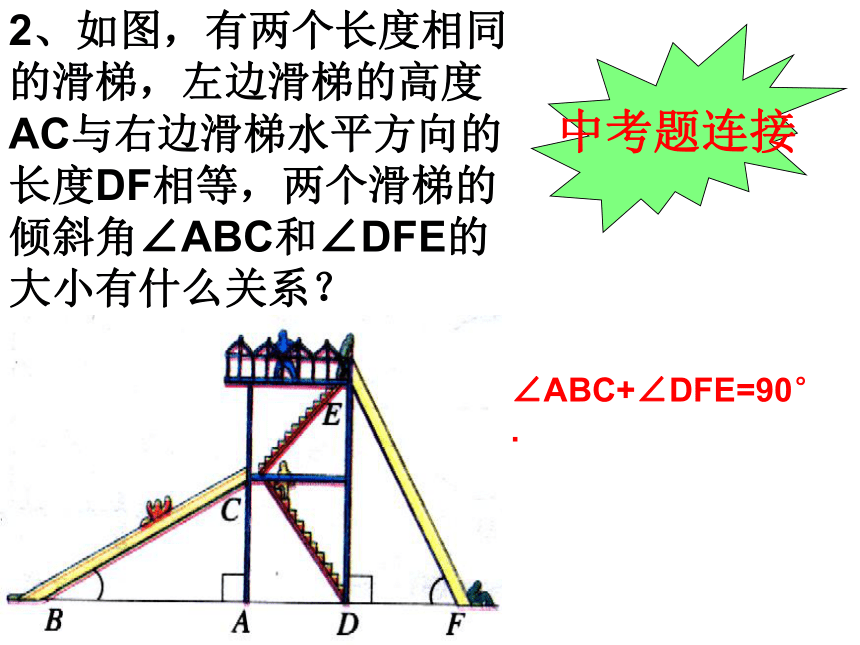
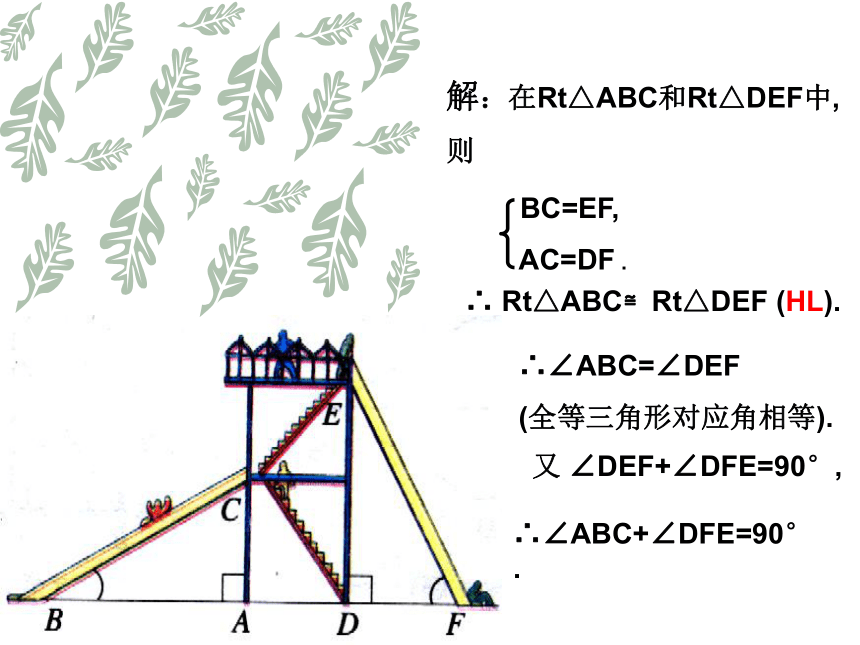
则∠ECF的度数=______度.三角形的中线、角平分线、高线的概念练一练:10.5905、如图，在△ABC中，BD平分∠ABC，CE是AB边上的高，BD，CE交于点P。已知∠ABC=600，∠ACB=700, 求∠ACE，∠BDC的度数。400800ABCEDF4.如图，AD、BF都是△ABC的高线，若∠CAD=30度，则∠CBF=______度。30二、全等三角形知识结构全等三角形定义：能够 的两个三角形对应元素：对应_____、对应 、对应 。性质：全等三角形的对应边 、 。判定： 、 、 、 、HL。完全重合边角相等对应角相等SSSSASASAAAS顶点例1：如图，AC⊥BC,AD⊥BD,垂足分别为C、D，AC=BD,Rt△ABC与Rt△BAD全等吗？为什么？知识运用ACBOD1、如图:AC和DB相交于点O,若AB=DC，AC=DB，则∠B=∠C,请说明理由.思考题：中考题连接 2、如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系？∠ABC+∠DFE=90°.解：在Rt△ABC和Rt△DEF中,
则∴ Rt△ABC≌Rt△DEF (HL).∴∠ABC=∠DEF
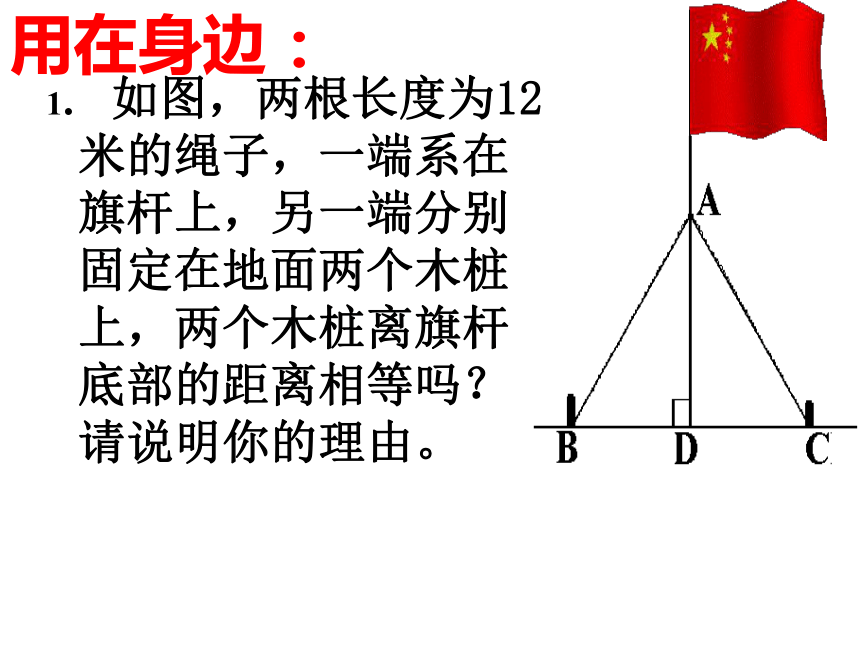
(全等三角形对应角相等).又 ∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°.1. 如图，两根长度为12米的绳子，一端系在旗杆上，另一端分别固定在地面两个木桩上，两个木桩离旗杆底部的距离相等吗？请说明你的理由。用在身边：中考题连接 小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?AB利用“角边角”可知,带B块去，可以配到一个与原来全等的三角形玻璃。AB议一议 小明的设计方案：先在池塘旁取一个能直接到达A和B处的点C，连结AC并延长至D点，使AC=DC，连结BC并延长至E点，使BC=EC，连结CD，用米尺测出DE的长，这个长度就等于A，B两点的距离。请你说明理由。 AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE(SAS)
AB=DEECBAD如图线段AB是一个池塘的长度，
现在想测量这个池塘的长度，在
水上测量不方便，你有什么好的
方法较方便地把池塘的长度测量
出来吗？想想看。　１、三角形的两边长分别是3和 5，第三边a的取值范围（ ） A、2≤a＜8 B、2＜a≤8  C、2＜a＜8 D、2≤a≤8基础训练C２、能把一个三角形分成面积相等的两部分是三角形的（ ）
A、中线
B、高线
C、角平分线
D、过一边的中点且和这条边垂 直的直线基础训练A３、在△ABC中，若∠A=54°，∠B=36°，则△ABC是（ ）
A、锐角三角形 B、钝角三角形
C、直角三角形 D、等腰三角形基础训练C4、如图AD=BC，要判定 △ABC≌△CDA，还需要的条件是 　　 .
基础训练ＡＢ＝ＣＤ或∠ＤＡＣ＝∠ＢＣＡ 5、如图，∠1=∠2，AB=CD，AC与BD相交于点O，则图中必定全等的三角形有（ ）
A. 2对 B. 3对
C. 4对 D. 6对C小 结1.学习了本节课以后,你有哪些 收获?
2.你还有什么疑惑?再创辉煌：1、如图∠ACB=∠DFE，BC=EF，根据ASA或AAS，那么应补充一个直接条件 --------------------------，（写出一个即可），才能使△ABC≌△DEF2、如图，BE=CD，∠1=∠2，则AB=AC吗？为什么？ABCDEF∠B=∠E或∠A=∠D10、要画出∠AOB的平分线，分别在OA，OB上截取OC=OD，OE=OF，连结CF，DE，交于P点，那么∠AOB的平分线就是射线OP，要说明这个结论成立，可先说明△EOD≌ △ 　　 . 理是 　　　　 ，得到　∠OED=∠ 　　　　　　 ，再说明△PEC≌△ 　　　 ，理由是 　　　　 ，得到PE= 　　　　　　　　 ；最后说明△EOP≌△ 　　　　　　　　 ，理由是 　　　　　　　　　　　　　 ，从而说明了∠AOP=∠BOP，即OP平分∠AOB。
ＦＯＣＳＡＳＯＦＣＰＦＤＡＡＳＰＦＦＯＰＳＡＳ阅读理解１、如图，BE、CF是△ABC 的角平分线，∠A=40°。则∠BOC=（ ）度
A、70 B、110
C、120 D、140巩固练习B２、如图，已知△ABC中，∠B=45°，∠C=75°，AD是BC边上的高，AE是∠BAC的平分线，∠DAE=（ ）度。
A、15 B、30 C、45 D、25A3、下列各组数中不可能是一个三角形的边长　的是（ ）
A.5，12，13 　　B. 5，7，7
C. 5，7，12 　 D. 101，102，103 4、已知一个三角形的三条高的交点不在这个三角形的内部，则这个三角形（ ）
A. 必定是钝角三角形 B. 必定是直角三角形
C. 必定是锐角三角形 D. 不可能是锐角三角形CD6、已知等腰三角形底边为8，一腰上的中线分此三角形的周长成两部分，其差为2，则腰长为 .7、如图，AD是△ABC的高，且AD平分∠BAC，请指出∠B与∠C的关系，并说明理由。 6或８8、如下图，已知AD是△ABC的中线，CE是△ADC的中线，若△ABC的面积是8，求△DEC的面积。9、如上图，△ABC中，点D是BC上的一点，点E是AD上的一点，若BD:CD=2:3 ，DE:AE=1:4 ，△ABC的面积是8，求△DEC的面积。ABCDE如图要测量河两岸相对的两点A、B的距离，先在AB 的垂线BF上取两点C、D，使CD=BC，再定出BF的垂线DE，可以证明△EDC≌△ABC，得ED=AB，因此，测得ED的长就是AB的长。判定△EDC≌△ABC的理由是( )
A、SSS B、ASA C、AAS D、SASB做一做，比比看谁的速度快！ 小明在上周末游览风景
区时，看到了一个美丽的
池塘 ，他想知道最远两点
A、B之间的距离，但是他没有船，不能直接去测。
手里只有一根绳子和一把尺子，他怎样才能测出A、
B之间的距离呢？
把你的设计方案在图上画出来，并与你的同伴
交流你的方案，看看谁是方案更便捷。AB●●A、B间有多远呢？想一想AB●●●CED 在能够到达A、B的空地上取一适当点C，连接AC，并延长AC到D，使CD=AC，连接BC，并延长BC到E，使CE=BC，连接ED。则只要测出
ED的长就可以知道AB的长了。理由如下: 在△ACB与△DCE中，∠BCA=∠ECDAC=C DBC=CE全等三角形的对应边相等练一练：1、完成下列推理过程：在△ABC和△DCB中，∴△ABC≌△DCB（ ）ASA（ ） 公共边∠1=∠2∠3=∠4AASFEDCBA如图，∠B＝∠E，AB＝EF，BD＝EC，那么△ABC与　△FED全等吗？为什么？解：全等。∵BD=EC（已知）　　　∴BD－CD＝EC－CD。即BC＝ED　　在△ABC与△FED中∴△ABC≌△FED（SAS）AC∥FD吗？为什么？∴∠1＝∠2（　）∴∠3＝∠4（　）∴AC∥FD（内错角相等，两直线平行4321