华师大版 八年级下册 第17章 函数及其图象反比例函数图像及其性质作业设计
文档属性
| 名称 | 华师大版 八年级下册 第17章 函数及其图象反比例函数图像及其性质作业设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 172.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 00:00:00 | ||
图片预览


文档简介
八年级数学作业设计
作业设计团队所在学校(签章):
作业涉及教科书版本:华东师大版 年级及册次:八年级下册
作业涉及单元、章节(或主题、任务):17.4.2 反比例函数的图象及性质
作业设计团队教师姓名:
本单元内容属于《义务教育课程标准实验教科书》“数与代数”领域,而本节内容是学生在学面直角坐标系、一次函数以及反比例函数定义的基础上,再一次进行函数的学习。通过让学生图象及其性质的学习,让学生进一步理解函数的内涵,并感受函数存在现实生活中以及如何运用函数解决设计问题。反比例函数是最基本的函数之一,它是建立在一次函数的基础上,同时由为以后学习更高层次的函数奠定了基础。因此本单元教学内容起到承上启下,举足轻重的地位。以下是本单元的作业设计意图: 1、立足教材、注重基础、整体设计。 单元作业设计以新课标为依据,以学情为出发点,以教材为主要来源.与单元教学目标相契合,整体架构,相互联动,构建起学科育人的完整体系,结合教材和学情,体现“教学和作业”的开放性。 ⒉.面向全体,分层发展 基础作业主要对标“四基”中基础知识的过关和基本技能的过手,让学生感悟数学的基本思想.发展性作业则主要设计成以数学应用、数学实践、项目式学习和跨学科学习等形式的创新作业,让不同水平的学生都能不同程度地卷入其中,沉浸式、参与式和体验式完成作业,在积累基本活动经验的同时,培养学生发现问题、提出问题、分析问题和解决问题的能力. 3.联系生活,提升素养 作业在纵向分为课前、课中、课后三个部分,横向分为基础性作业和发展性作业两种类型,层次递进,并且螺旋上升,促进学生数学眼光、数学思维和数学语言的持续发展.同时,很多作业都取材于学生身边熟悉的情境和真实的问题,并适当引入一些结构不良问题,培养学生数学阅读、抽象思维、数学建模等能力,在探究和应用中实现学科的育人价值.
第 1 课时
使 用时段 作 业内容 作业设计 设计意图 使 用者 预 计时长 预 估难度系数
课前 基础性作业 作业一: 探究:画反比例函数 y=6和 y= 6的函数图 象?观察图象的共同点和异同点?结论: 1、这两个函数图象是什么,y 值可以为 0吗?这个函数图象与x 轴y 轴有没有交点? 2、由两个分支组成的双曲线,双曲线无限接近于于 。x 与 y 所取值的符号有什么关系? 这个函数图象会在哪几个象限? 如果 k>0, x,y 所取值的符号 ,函数图象在 象限;如果 k<0,x,y 所取值的符号函数图象在 象限。 3、这两个图象有什么变化趋势?当 k>0 时 当 k<0 时 本题通过作 图使学生自行发现并归纳反比例函数的性质。 本题通过填空形式将新课必备知识以结构化。 本题为课上反比例函数的图象与性质奠定基础 全 体学生 4 分钟 0.9
发 展性作业 作业二: 作图求取值范围: 4、已知反比例函数 y=2,当-2≤x≤-1 时, y 的取值范围。 本题反比例 函数性质的拓展性应用,培养学生数学建模思维、逻辑推理能力和应用与创新意识。 绝 大多数学生 4 分钟 0.8
课中 基础性 作业三: 5、学生先复习一次函数和正比例函数的图象及性质 本题学生 类比一次函数和正比例函数的图象解决反比例函数对的图象和性质。 全 体学生 3 分钟 0.9
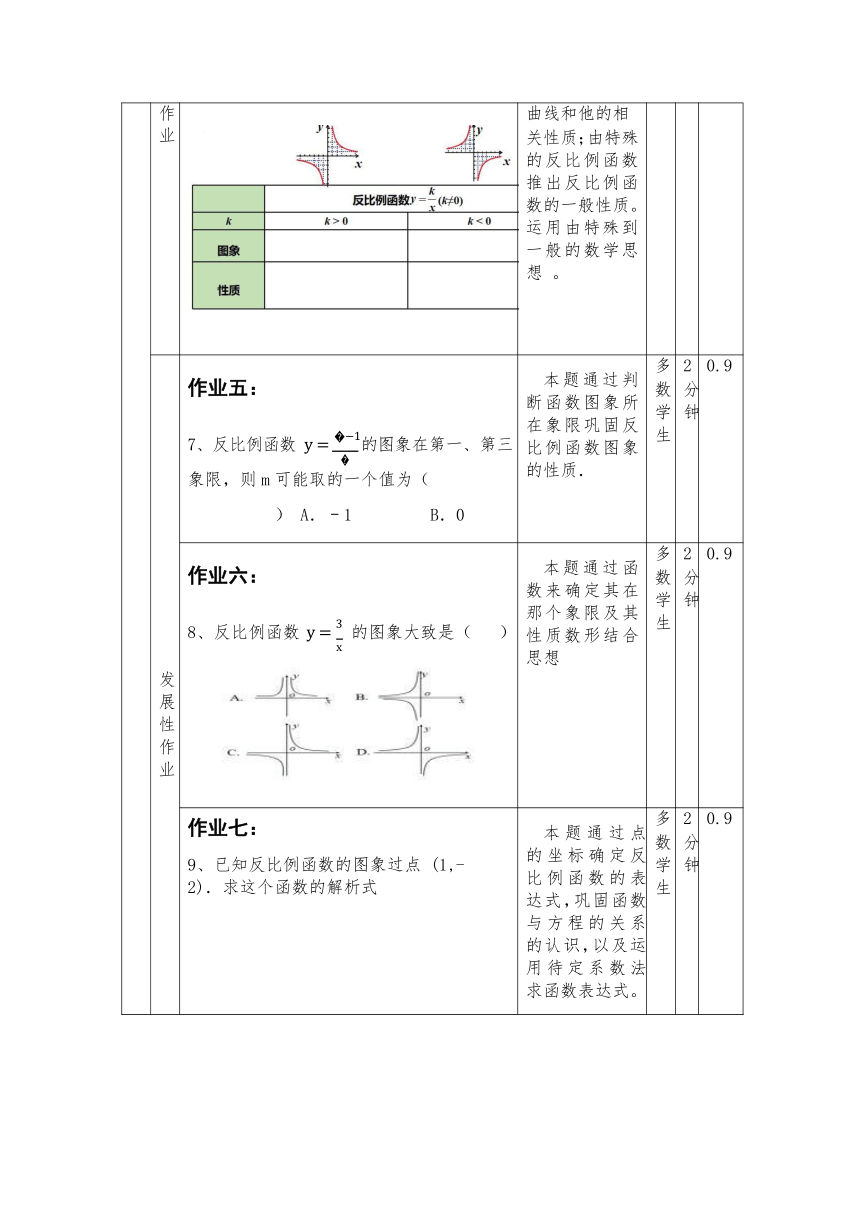
作业四: 6、画出反比例函数的图形和性质 本题利用数形结合的思想的出反比例函数的图象是双 全 体学生 3 分钟 0.8
作 业 曲线和他的相 关性质;由特殊的反比例函数推出反比例函数的一般性质。运用由特殊到一般的数学思想 。
发展性作业 作业五: 7、反比例函数 y = 1的图象在第一、第三 象限,则 m 可能取的一个值为( ) A.﹣1 B.0 C.1 D.2 本题通过判断函数图象所在象限巩固反比例函数图象的性质. 多 数学生 2 分钟 0.9
作业六: 8、反比例函数 y = 3 的图象大致是( ) x 本题通过函数来确定其在那个象限及其性质数形结合思想 多 数学生 2 分钟 0.9
作业七: 9、已知反比例函数的图象过点 (1,-2).求这个函数的解析式 本题通过点的坐标确定反比例函数的表达式,巩固函数与方程的关系的认识,以及运用待定系数法求函数表达式。 多 数学生 2 分钟 0.9
课后 基础性作业 作业八: 10、对于反比例函数 y 2 ,下例说法错 x 误的是( ) A、点(2,-1)在它的图象上; B、它的图象在第二、四象限内; C、当 x>0 时,y 随 x 的增大而增大 ; D、它的图象的两个分支关于 y 轴对称。 本题是为了解 学生掌握基础知识的情况。是否真正理解反比例函数的图象和性质。 全 体学生 2 分钟 0.8
作业九: 11、点 P 在反比例函数 y = 6 的图象上 x 一点,PA⊥x 轴于 A,O 为坐标原点,则△AOP的面积是 。 本题是对反比 例函数的图象及性质、三角形的面积的考查。 全 体学生 3 分钟 0.8
发展性作业 作业十: 12、消杀新冠病毒,学校对教室进行“药熏消毒”。已知药物燃烧时,室内每立方米空气中含药量 y(mg)与燃烧时间 x(min)成正比例,燃烧后,y 与 x 成反比例(如图所示)。现测得药物 8 分钟燃烧完毕,此时教室内每立方米空气中含药量为 6mg。根据以上信息: (1)求药物燃烧时和燃烧后 y 与 x 的函数关系式。 (2)研究表明,当空气中的含药量低于 1.6mg/m3 时,学生才能回到教室,那么从消毒开始学生需要经过多长时间才能回到教室?(课后一周内完成,可以通过上网查阅相关消杀资料,可以互相讨论得出结论) y(mg/m3) 6 0 8 x(min) 本题主要了解 学生的视图能力,利用图象解决不等式解决实际问题的能力,利用待定系数法求函数表达式。待定系数法是基本的数学方法。针对学生作业的情况,采取必要的方法补救。 大 部分学生 1 0 分钟 0.7
附:
第 1 课时
参考答案
课前:作业一:1、是双曲线;y 值不可以为 0;与 x,y 轴无交点;
2、坐标轴;同号,一、三;异号,二、四;
3、在每一个象限 y 随 x 的增大而减小;在每一个象限 y 随 x 增大而增大;作业二:4、 2 ≤ y ≤ 1;
课中:作业三:5、
作业四:6、
作业五:7、D;作业六:8、C;
作业七:9、解:设反比例函数解析式为 y = k过点(1,-2)
x
所以 2 = k,k=-2
1
所以 y = 2;
x
课后:作业八:10.D;作业九:11、3;
作业十:
12、(1)由图象可知:
药物燃烧时是正比例函数、燃烧后是反比例函数,它们都经过点(8,6)
设正比例函数的表达式为:y = kx;设反比例函数的表达式为 y = m
x
∴6 = 8k 6 = m 8
∴k = 3 ; m = 24
4
∴药物燃烧时和燃烧后的函数关系式分别为 y = 3 x, y = 24
4 x
(2)∵反比例函数的 k=24>0,y 随 x 的增大而减小,当 y 减小,x 就增大。
∴当 y = 1.6 时,1.6 = 24∴x = 15 ∵y < 1.6 ∴ > 15
x
答:从消毒开始学生需要经过 15 分钟才能回到教室。
作业设计团队所在学校(签章):
作业涉及教科书版本:华东师大版 年级及册次:八年级下册
作业涉及单元、章节(或主题、任务):17.4.2 反比例函数的图象及性质
作业设计团队教师姓名:
本单元内容属于《义务教育课程标准实验教科书》“数与代数”领域,而本节内容是学生在学面直角坐标系、一次函数以及反比例函数定义的基础上,再一次进行函数的学习。通过让学生图象及其性质的学习,让学生进一步理解函数的内涵,并感受函数存在现实生活中以及如何运用函数解决设计问题。反比例函数是最基本的函数之一,它是建立在一次函数的基础上,同时由为以后学习更高层次的函数奠定了基础。因此本单元教学内容起到承上启下,举足轻重的地位。以下是本单元的作业设计意图: 1、立足教材、注重基础、整体设计。 单元作业设计以新课标为依据,以学情为出发点,以教材为主要来源.与单元教学目标相契合,整体架构,相互联动,构建起学科育人的完整体系,结合教材和学情,体现“教学和作业”的开放性。 ⒉.面向全体,分层发展 基础作业主要对标“四基”中基础知识的过关和基本技能的过手,让学生感悟数学的基本思想.发展性作业则主要设计成以数学应用、数学实践、项目式学习和跨学科学习等形式的创新作业,让不同水平的学生都能不同程度地卷入其中,沉浸式、参与式和体验式完成作业,在积累基本活动经验的同时,培养学生发现问题、提出问题、分析问题和解决问题的能力. 3.联系生活,提升素养 作业在纵向分为课前、课中、课后三个部分,横向分为基础性作业和发展性作业两种类型,层次递进,并且螺旋上升,促进学生数学眼光、数学思维和数学语言的持续发展.同时,很多作业都取材于学生身边熟悉的情境和真实的问题,并适当引入一些结构不良问题,培养学生数学阅读、抽象思维、数学建模等能力,在探究和应用中实现学科的育人价值.
第 1 课时
使 用时段 作 业内容 作业设计 设计意图 使 用者 预 计时长 预 估难度系数
课前 基础性作业 作业一: 探究:画反比例函数 y=6和 y= 6的函数图 象?观察图象的共同点和异同点?结论: 1、这两个函数图象是什么,y 值可以为 0吗?这个函数图象与x 轴y 轴有没有交点? 2、由两个分支组成的双曲线,双曲线无限接近于于 。x 与 y 所取值的符号有什么关系? 这个函数图象会在哪几个象限? 如果 k>0, x,y 所取值的符号 ,函数图象在 象限;如果 k<0,x,y 所取值的符号函数图象在 象限。 3、这两个图象有什么变化趋势?当 k>0 时 当 k<0 时 本题通过作 图使学生自行发现并归纳反比例函数的性质。 本题通过填空形式将新课必备知识以结构化。 本题为课上反比例函数的图象与性质奠定基础 全 体学生 4 分钟 0.9
发 展性作业 作业二: 作图求取值范围: 4、已知反比例函数 y=2,当-2≤x≤-1 时, y 的取值范围。 本题反比例 函数性质的拓展性应用,培养学生数学建模思维、逻辑推理能力和应用与创新意识。 绝 大多数学生 4 分钟 0.8
课中 基础性 作业三: 5、学生先复习一次函数和正比例函数的图象及性质 本题学生 类比一次函数和正比例函数的图象解决反比例函数对的图象和性质。 全 体学生 3 分钟 0.9
作业四: 6、画出反比例函数的图形和性质 本题利用数形结合的思想的出反比例函数的图象是双 全 体学生 3 分钟 0.8
作 业 曲线和他的相 关性质;由特殊的反比例函数推出反比例函数的一般性质。运用由特殊到一般的数学思想 。
发展性作业 作业五: 7、反比例函数 y = 1的图象在第一、第三 象限,则 m 可能取的一个值为( ) A.﹣1 B.0 C.1 D.2 本题通过判断函数图象所在象限巩固反比例函数图象的性质. 多 数学生 2 分钟 0.9
作业六: 8、反比例函数 y = 3 的图象大致是( ) x 本题通过函数来确定其在那个象限及其性质数形结合思想 多 数学生 2 分钟 0.9
作业七: 9、已知反比例函数的图象过点 (1,-2).求这个函数的解析式 本题通过点的坐标确定反比例函数的表达式,巩固函数与方程的关系的认识,以及运用待定系数法求函数表达式。 多 数学生 2 分钟 0.9
课后 基础性作业 作业八: 10、对于反比例函数 y 2 ,下例说法错 x 误的是( ) A、点(2,-1)在它的图象上; B、它的图象在第二、四象限内; C、当 x>0 时,y 随 x 的增大而增大 ; D、它的图象的两个分支关于 y 轴对称。 本题是为了解 学生掌握基础知识的情况。是否真正理解反比例函数的图象和性质。 全 体学生 2 分钟 0.8
作业九: 11、点 P 在反比例函数 y = 6 的图象上 x 一点,PA⊥x 轴于 A,O 为坐标原点,则△AOP的面积是 。 本题是对反比 例函数的图象及性质、三角形的面积的考查。 全 体学生 3 分钟 0.8
发展性作业 作业十: 12、消杀新冠病毒,学校对教室进行“药熏消毒”。已知药物燃烧时,室内每立方米空气中含药量 y(mg)与燃烧时间 x(min)成正比例,燃烧后,y 与 x 成反比例(如图所示)。现测得药物 8 分钟燃烧完毕,此时教室内每立方米空气中含药量为 6mg。根据以上信息: (1)求药物燃烧时和燃烧后 y 与 x 的函数关系式。 (2)研究表明,当空气中的含药量低于 1.6mg/m3 时,学生才能回到教室,那么从消毒开始学生需要经过多长时间才能回到教室?(课后一周内完成,可以通过上网查阅相关消杀资料,可以互相讨论得出结论) y(mg/m3) 6 0 8 x(min) 本题主要了解 学生的视图能力,利用图象解决不等式解决实际问题的能力,利用待定系数法求函数表达式。待定系数法是基本的数学方法。针对学生作业的情况,采取必要的方法补救。 大 部分学生 1 0 分钟 0.7
附:
第 1 课时
参考答案
课前:作业一:1、是双曲线;y 值不可以为 0;与 x,y 轴无交点;
2、坐标轴;同号,一、三;异号,二、四;
3、在每一个象限 y 随 x 的增大而减小;在每一个象限 y 随 x 增大而增大;作业二:4、 2 ≤ y ≤ 1;
课中:作业三:5、
作业四:6、
作业五:7、D;作业六:8、C;
作业七:9、解:设反比例函数解析式为 y = k过点(1,-2)
x
所以 2 = k,k=-2
1
所以 y = 2;
x
课后:作业八:10.D;作业九:11、3;
作业十:
12、(1)由图象可知:
药物燃烧时是正比例函数、燃烧后是反比例函数,它们都经过点(8,6)
设正比例函数的表达式为:y = kx;设反比例函数的表达式为 y = m
x
∴6 = 8k 6 = m 8
∴k = 3 ; m = 24
4
∴药物燃烧时和燃烧后的函数关系式分别为 y = 3 x, y = 24
4 x
(2)∵反比例函数的 k=24>0,y 随 x 的增大而减小,当 y 减小,x 就增大。
∴当 y = 1.6 时,1.6 = 24∴x = 15 ∵y < 1.6 ∴ > 15
x
答:从消毒开始学生需要经过 15 分钟才能回到教室。
